优化高等数学成绩评价的数学实验*
2014-08-08陈士龙张玉香
陈士龙,张玉香
(安徽广播影视职业技术学院基础教学部,安徽合肥230011)
1 问题的提出
高等数学是高校理工类专业重要的基础课,在学生专业课的学习过程中,高等数学的重要性和必要性是不言而喻的.对学生的高数成绩进行合理的评价是教学过程中十分重要的环节,而在评价的过程中,要考虑到评价的全面性、合理性和科学性,不仅包括学生数学知识的掌握情况和解题能力,还包括学生学习的实际能力等方面,因此有必要采用层次分析法构建数学模型以便能够多角度、全方位地对学生的数学成绩进行评价.
2 数学模型的建立
2.1 模型假设
(1)期末考试的成绩实行百分制;
(2)最终成绩是通过课堂表现、平时成绩和期末考试成绩来确定;
(3)平时不出现旷课和不交作业的情况;
(4)每个学生处于相同的考试环境中;
(5)考试中每位学生的成绩为真实的,作业独立完成,期末考试不存在作弊的情况发生.
2.2 模型的建立
为了合理的对数学成绩进行评价,要考虑到影响成绩的各个方面,所以在建立数学模型时,把学生成绩评价作为目标层,将平时成绩、课堂表现和期末成绩作为第二层,也就是准则层,为了全面衡量准则层,又将其分为计算能力、逻辑思维能力、数学基础能力和数学创新能力.

图1 成绩评价分层图示
在准则层中,根据课堂表现、平时成绩和期末考试成绩对目标层的权重,建立比较判断矩阵,用常用的1~9的比较尺度,建立判断矩阵得
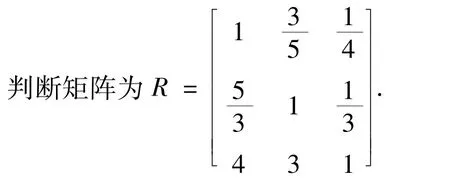
计算判断矩阵的特征值,得最大特征值为λmax=3,ω0=(0.5313,0.8855,2.1253),,判断矩阵的一致性指标CI=,平均随机一致性指标RI=0.58,一致性比率CR=0<0.1,可以认为判断矩阵具有满意的一致性,表明以W=(0.15,0.25,0.6)T的各个分量w作为相应的各个因素的权重值分配是合理的,W=(0.15,0.25,0.6)T可以作为权向量.
二级准则层中共有4个影响因素,分别属于课堂表现和平时成绩,它们的判断矩阵分别设为:

判断矩阵B2的一致性指标,平均随机一致性指标RI=0,一致性比率CR=0<0.1.
下面将上面的目标层对准则层,准则层对子准则层,各种影响因素进行总的排序,确定各因素对目标层的权重,见表1.

表1 成绩评价准则层权重图示

表2 成绩评价转化结果图示
现在以10名学生的成绩为例,说明学生成绩的评价过程.在表2的成绩构成中,对于数学基础知识、数学创新能力、数学计算能力和逻辑思维能力的成绩进行等级打分,即教师按照教学过程中学生的实际情况,分别将这几个方面的成绩评定为A、B、C和D,由于要将这几个数据进行数字转换,故将它们对应于数字 5、4、3、2.
根据偏大型柯西隶属函数

据经验公式规定,当评价为A时,则隶属度为1,即f(5)=1,;当评价为C时,则隶属度为0.8,即f(3)=0.8;当评价为D时,则隶属度为0.01,于是可解出 α =1.1086,β =0.8942,a=0.3915,b=0.3699,可以解出f(4)=0.9126,f(2)=0.5425,可以对应于教师对学生的评价量化为(1,0.9126,0.8,0.5425),则子准则层四个因素对应的百分比分数,以及期末的成绩分别为表3:

表3 成绩评价对应百分比结果图示

表4 综合成绩汇总
根据表1中四个分量的总排序,利用加权以及各个分量的百分比,就可以算出这10名学生总的数学评价成绩.
3 结束语
(1)本文提供的评价方法和思路,更多的是关注评价的全面性和科学性,是力求更全面地对学生的综合素质进行评价.就评价的范围而言,则适合于理论性的学科,对实践性较强的学科,则需要确立与实践相关的目标层、准则层和子准则层,建立与实践相适应的模型,从而建立适合实践性学科的评价方法.
(2)评价的方法具有一定的抽象性和理论性,在用数学模型解决实际问题的过程中,当然要对所要解决的问题进行数学抽象和前提假设.本文提供的方法具体到相当多的高职院校的学生,则会产生一定的误差,比如在建立模型的假设中,存在着很多学生难以独立完成作业,学习的自觉性较差,数学的基础比较薄弱等情况,这就会在子准则层的评定上存在误差.
[1]唐秋晶.运用数理统计方法评价学生的学习状况[J].济宁师专学报,1998(6).
[2]韩中庚.招聘公务员问题的优化模型与评述[J].工程数学学报,2004(4).
[3]姜启源,谢金星,叶俊.数学建模[M].北京:高等教育出版社,2003.
[4]高隆昌,杨元.数学建模基础理论[M].北京:科学出版社,2007.
