帆船VMG时间序列模糊边界研究

高慧，潘明杰，周翔，任久春，朱谦

帆船VMG时间序列模糊边界研究

高慧，潘明杰，周翔，任久春，朱谦

VMG（Velocity Made Good）是帆船在前进过程中船速在风的方向上的投影，它体现了帆船在风向上前进的能力，反映了帆船运动员利用风的能力。因此，对运动员而言，若能掌握VMG的变化范围，即为他们制定帆船航行方向决策提供了科学依据。基于与上海体育局合作的《帆船帆板赛场环境监测和运动技术分析系统开发》课题所采集到的有关帆船运动的原始数据，首先，采用基于模糊集的信息粒化方法将原始数据粒化，得到VMG的模糊粒子；之后，采用支持向量机（Support Vector Machine，SVM）的学习方法实现对模糊粒子的上下界的回归预测，从而实现了帆船VMG时间序列的模糊边界的变化范围预测。实验仿真结果证明了这种研究方法的有效性。

VMG；时间序列预测；支持向量机；信息粒化；模糊边界

0 引言

现代帆船运动已经成为世界沿海地区人们喜闻乐见的体育项目之一。帆船比赛是运动员驾驶帆船在规定海域内竞赛的运动，运动员的海风利用技能对比赛结果有重大的影响。VMG（Velocity Made Good）即是描述运动员利用海风技能的重要参数，它为运动员制定帆船航行决策提供了重要的依据。因此，若能实现对VMG的变化趋势的预测，可以科学改进训练方法，提高运动员的竞技水准。

目前，在帆船运动研究领域，很多科学家都把目光聚焦在帆船船体力学与海面环境参数[1]的相关研究。如D.Detomi[2]等人利用数学建模的方法模拟了帆船的受力分析情况。从机器学习的角度来对帆船运动提供科学指导的研究很少。本文基于与上海体育局合作的项目，即前期我们已经获得了很多有关帆船运动的数据，如风速，风向，船速，船向，帆船的几种倾角等，如表1所示：

表1 符号对照表

现在，我们期望通过一种机器学习方法-支持向量机来实现对帆船VMG的未来变化范围的预测。从而为帆船运动员制定航行方向决策提供依据，提高运动员的比赛成绩。

支持向量机（Support Vector Machine）是Vapnik于1995年提出[3]，由于具备收敛速度快，计算简单等诸多优点，现已被广泛应用到模式识别与回归预测问题。起初，支持向量机是用来解决分类问题的一种非常有效的算法，后来经引入ε不敏感损失函数将其应用至非线性回归预测问题。目前，支持向量机已经成功应用到很多领域的预测问题，如电力系统负荷预测[4]，金融领域预测[5]，时间序列预测[6,7]，空中交通流量组合预测[8]等。但是，传统的支持向量机回归预测是单步的，即只能实现对下一时刻状态的预测。对于帆船运动教练员及运动员，他们不仅期望能掌握下一时刻的预测结果，更希望获得VMG未来变化范围，以此制定帆船航行决策。信息粒[9]刚好可以将时间序列模糊化为模糊信息粒序列。接着，再利用SVM对该模糊粒子的上下界进行回归预测，即可实现对VMG的变化范围的回归预测。

故此，本文以帆船VMG为预测研究对象，首先使用模糊信息粒化的方式将VMG时间序列粒化成模糊粒子序列，之后再运用支持向量机对模糊粒子的上下界进行回归预测。最终获得VMG的未来变化范围。

1 VMG时间序列的模糊信息粒化

1.1 VMG的计算

如图1所示：

图1 帆船运动产生的风，真风和相对风的速度三角形关系

VMG是帆船在前进时紧靠逆风或顺风方向上的速度,它是帆船速度矢量的一部分,代表帆船在风向上的前进速度。船速乘以其与真实风向夹角的余弦。其计算方式如公式（1）：

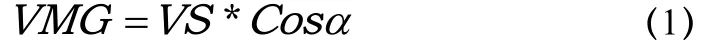
由于在测量过程中，船速VS，相对风速VA以及这两者之间的夹角（设为ϕ）通过一定的计算可以获得，如图1可知，利用矢量关系及余弦定理，我们即可求得VT以及cosα见公式（2）、（3）：

1.2 VMG模糊信息粒化

信息粒的概念最先是Zadeh[10]在1979年发表的文章《Fuzzy sets and information granularity》中提出。Zadeh 认为，作为存储和处理信息的一种方式，信息粒广泛存在于现实生活中。随后，信息粒便很快地引起了科学工作者的兴趣。1997年 T.Y.Lin[11]正式提出了粒计算的概念。随着研究工作的深入，粒计算目前有基于粗糙集模型[12]，基于商空间模型[13]，基于模糊集模型[14]及基于云模型等多种方式。随着大数据及机器学习的兴起，粒计算在知识发现，数据挖掘，海量信息处理及软计算等领域发挥越来越大的重要性。

信息粒化是基于相似度，一致性，功能性及可识别性聚集而成的一个实体。粒计算包含两个关键性的问题：粒化与基于粒化的计算。粒化是划分问题空间的过程。本文采用的是基于三角形模糊集的信息粒化方法，它是由荷兰学者F.J.M.Van Laarhoven和W.Pedrycz提出的“三角型”模糊粒子表示模糊比较判断的方法，如图2所示：

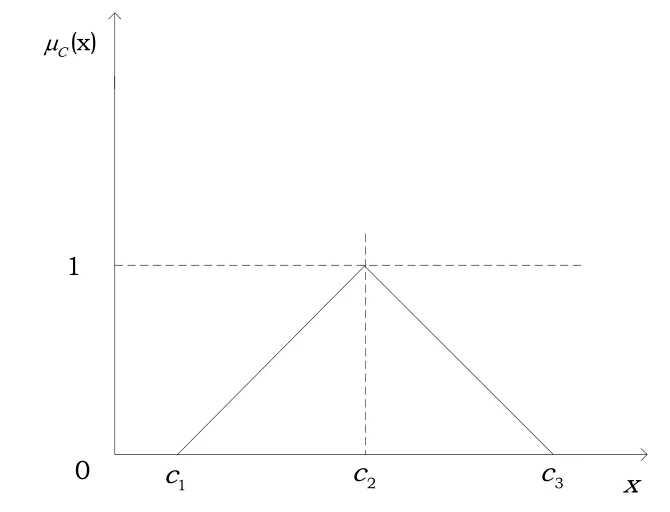
图2 模糊三角分布

算法可描述如下[15]：

算法1 W.Pedrycz 模糊粒化算法

输入： 时间序列数据

输出： 模糊化后的粒子

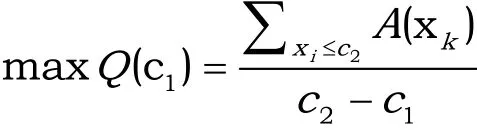
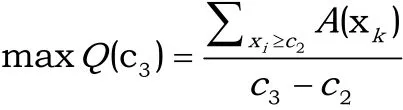
Step5：算法结束

有了模糊信息粒化的方法，对于给定的任意的时间序列，我们首先对该原始序列划分窗口，之后便可以利用该算法对其模糊粒化即可。

1.3 支持向量机

当SVM用于回归问题时，即被称为SVM回归机。给定一个训练样本，其中为输入数据为输出数据。对于SVM线性回归机，可用线性函数对样本数据进行拟合；对于SVM非线性回归机，可通过将样本空间映射到高维特征空间这样便又回归到线性回归支持向量机方法了。如此变换之后，可将非线性支持向量回归机的问题即转变为Hilbert空间的凸二次规划问题，可描述为公式（4）：

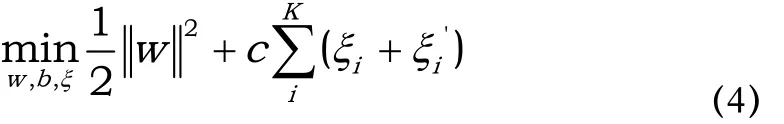
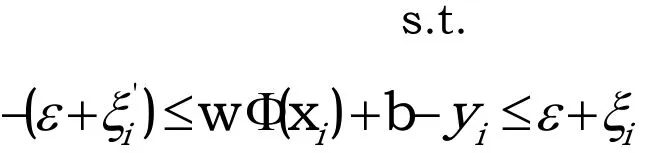
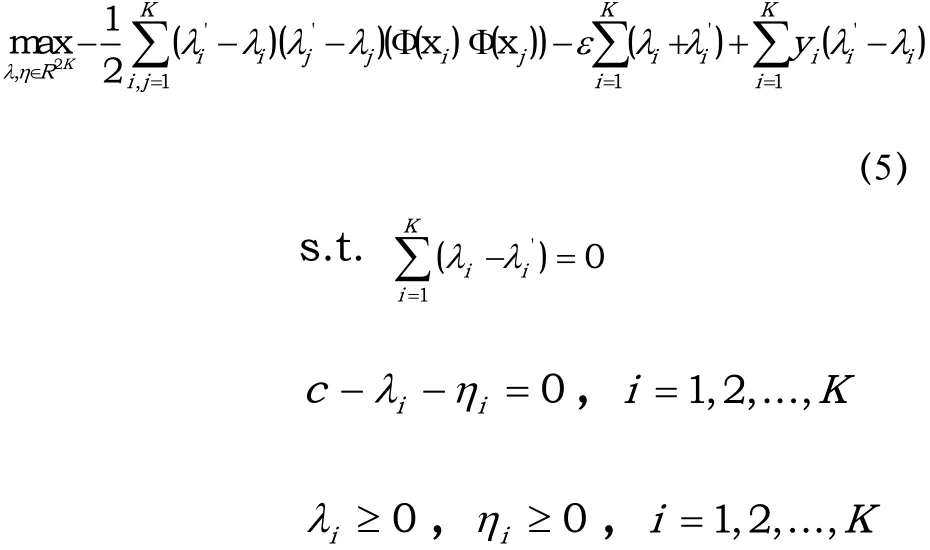
1.4 基于模糊信息粒化的支持向量机

本文首先采用模糊信息粒化对原始数据进行处理，之后再运用SVM回归预测模型来实现对船速，船向未来变化范围的预测。如此得到基于模糊信息粒化的支持向量机的算法流程图如图3所示：

图3 算法流程图

2 实验

2.1 实验数据和平台

本文以帆船运动的VMG为研究对象，利用上海体育局合作的《帆船帆板赛场环境监测和运动技术分析系统开发》课题所采集到的有关帆船运动的原始数据计算出帆船的VMG时间序列。数据选用的是2013年7月18日某个运动员训练时采集到的数据，共891条。数据是一个891*8的矩阵，每一行表示每一秒记录的有关帆船运动的各种指标，依次为VMG，VS，船向，VA，相对风向，γ，帆船前后倾角，帆船左右倾角。我们选用前887条作为训练数据集，第888条至第891条可作为预测结果验证数据。实验在Intel Core（TM）,i5-2400 CPU @ 3.10 GHz 3.09 GHz,内存为2.85GB的PC上执行。采用的是矩阵实验室（Matlab R2010b）及LIBSVM（3.17 Version）工具箱。

2.2 模糊粒化结果

对已得的VMG原始数据进行模糊粒化分为两个步骤：①选择粒化窗口大小，本文选择的粒化窗口大小是3；②对每个窗口数据执行算法1获得模糊信息粒，即用模糊信息粒表征原始数据。总共会得到296组参数模糊信息粒化后的可视图如图4所示：

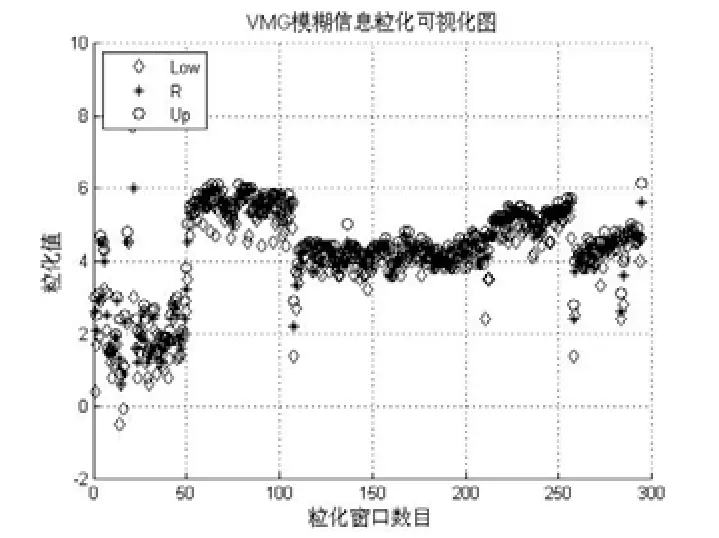
图4 VMG模糊粒化结果

由图4可知，粒化后的VMG时间序列走势与原始数据基本保持一致，即表明三角形模糊粒子可以很好的表征原始数据如表2所示：

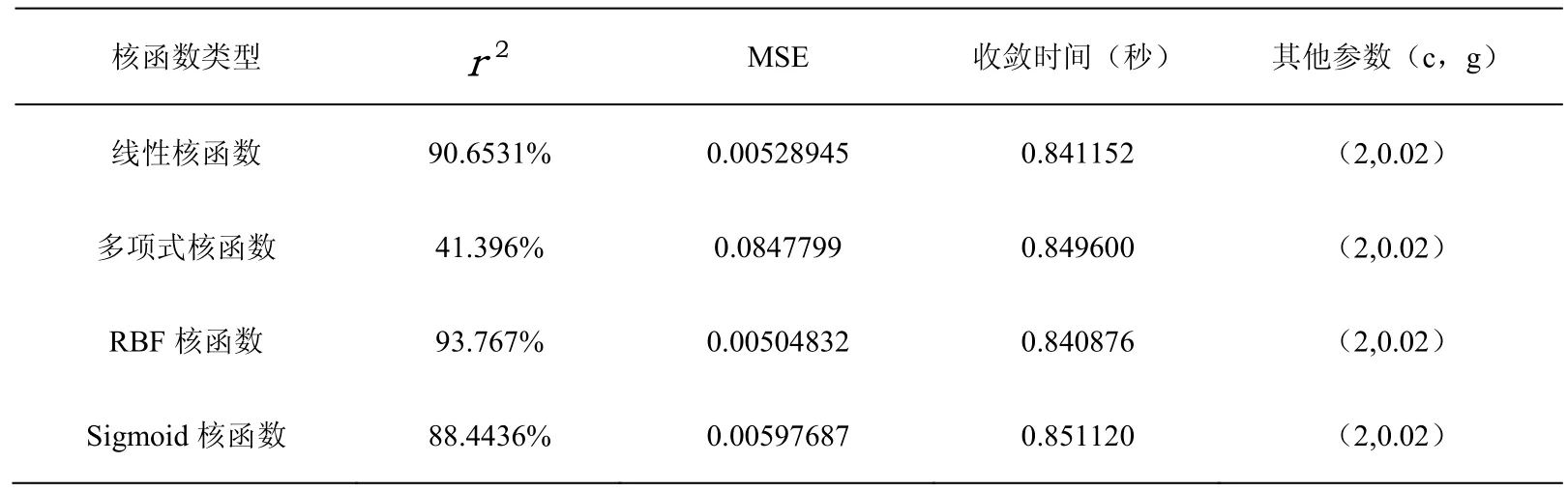
表2 不同核函数的预测性能比较

2.3 预测结果与分析

本文选用的是epsilon-SVM，关于核函数，经过大量实验并比较几种不同类型核函数的回归结果，最终选用的是RBF核函数（表2），采用网格搜索法进行惩罚因子c及核函数参数g寻优。粒化窗口是3，采用的是三角形模糊粒子。同时，为了提高SVM回归机的预测准确度，将原始VMG做了归一化处理。使用上文得到的模糊粒子作为SVM的训练数据集，对上界模糊集的核和下届分别做了回归预测，回归效果如图5、图6、图7所示：

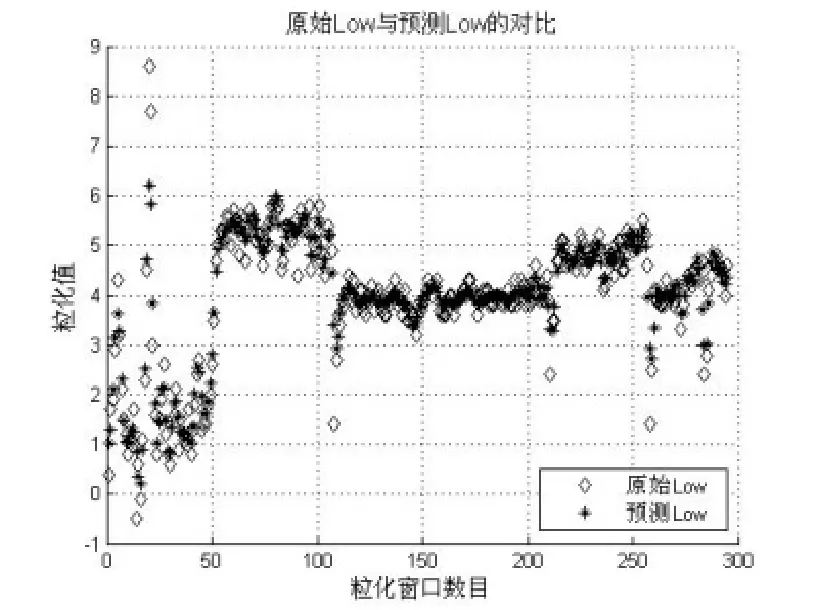
图5 对下界[Low]的回归结果

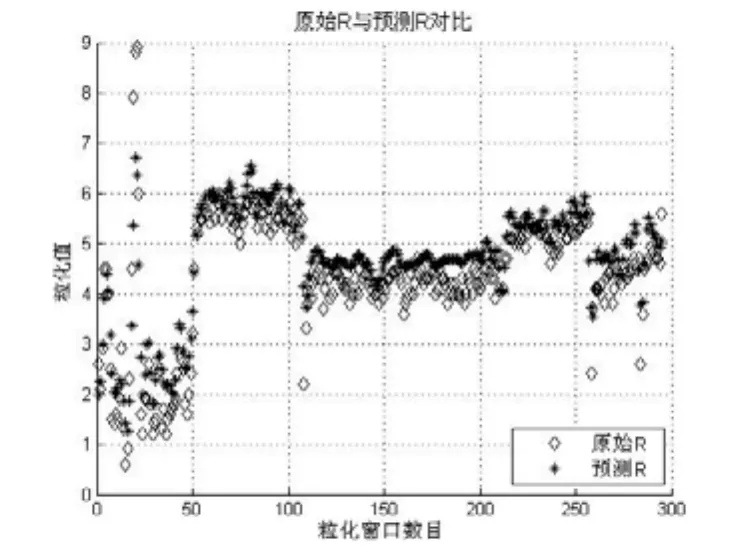
图6 模糊集核R的回归结果

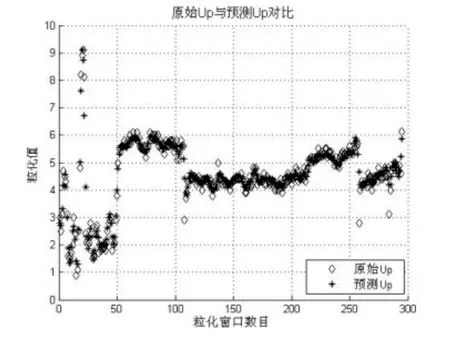
图7 上界[Up]的回归结果

由图5-图7可知，预测结果基本与实际值相符，趋势走向亦保持步调一致。这表明基于模糊信息粒化的SVM预测算法可以很好地追踪原始数据的变化范围。采用三角模糊粒化支持向量机对帆船VMG的区间预测结果如表3所示：

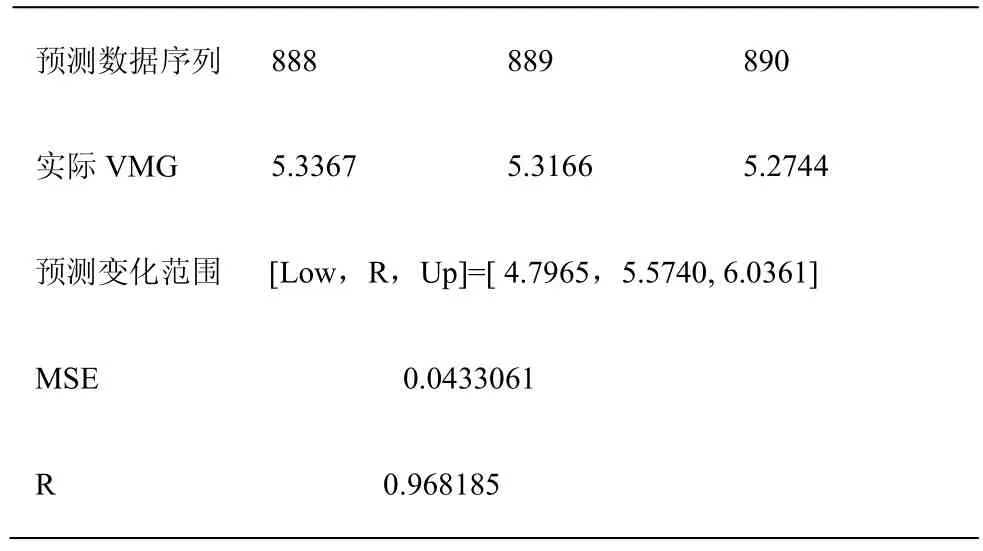
表3 VMG的区间预测结果（窗口数目：3）

其中，MSE与R是评价回归结果的参数指标，分别表示平均平方误差和平方相关系数。

由表3可知，预测结果完全覆盖了实际VMG的变化范围。这表明，基于模糊信息粒化的SVM预测算法可以准确地预测帆船VMG的变化范围，且预测结果可信。这样，帆船运动员和教练员便可以对VMG的变化范围有了大致的把握，进而可以制定出比较好的航行方向决策，提高比赛成绩。

3 总结

本文将支持向量机与信息粒化相结合对帆船VMG实行回归预测，预测结果是下一时间段的VMG的变化范围。实验结果表明基于模糊信息粒化的支持向量机方法可以准确地预测VMG的变化范围。VMG主要影响帆船运动员航行方向的决策，在很大程度上决定了帆船比赛的成绩，所以这个参数对运动员而言非常重要。因此，VMG变化范围的预测在协助帆船教练员对运动员进行科学的训练，提高比赛技能上具有重大的实际应用价值。

[1] Bryon D.Andson, The physics of sailing [J].Physicstoday, 2008, 61(2):38-43.

[2] D.Detomi,N. Parolini and A.Quarteroni, Mathematics in the Wind[J], Monografias de la Real Academia de Ciencias de Zaragoza 2009,31:35-56.

[3] Vapnik V. The nature of statistical learning theory [M]. New York: Springer—Verlag.1995.

[4] 李卜娟.基于LS-SVM的电力系统短期符合预测研究[D].南京:南京理工大学,2009.

[5] Suykens, Johan A K, Baestaens, et al. Financial time series predicton using least squares support vector machines within the evidence framework [J]. Neural Networks, 2001, (4):809-821.

[6] Maller K R, Smola A J, Ritsch Geta1. Predicting Time Series with Support Vector Machines [A]. In: Proc. of ICANN’97[C]. Springer Lecture Notes in Computer Science, 1997, 999—1005.

[7]Mukherjee S, Osuna E, Girosi F. Nonlinear Prediction of Chaotic Time Series Using Support Vector Machines [A]. In: Proc. of NNSP’97[C], 1997.

[8] 耿睿,崔德光,徐冰.应用支持向量机的空中交通流量组合预测模型[J].清华大学学报(自然科学版),2008,48(7): 1205-1208.

[9] 王国胤, 张清华,胡军.粒计算研究综述 [J].智能系统学报,2007,2(6):8-20．

[10] Zadeh L A. Fuzzy set s and information granulation advances in fuzzy set theory and applications [M]. Amsterdam: North2 Holland Publishing, 1979.

[11] Lin T Y. Granular Computing: From Rough Sets and Neighborhood Systems to Information Granulation and Computing in Words[C].European Congress on Intelligent Techniques and Soft Computing,1997,1602-1606.

[12] Pawlak Z. Rough Sets [J].International Journal of Information and Computer Sciences,1982,11(5):341-356.

[13] 张钹, 张铃.问题求解理论及应用[M].北京:清华大学出版社,1990.

[14] Zadeh L.A. Fuzzy sets [J]. Information and Control, 1965, 8(3):338-353.

[15] Pedrycz W. Knowledge-based clustering—from data to information granules [M].Wiley—Interscience, 2005.

[16] 邓乃扬,田英杰.支持向量机-理论,算法与拓展[M].北京:科学出版社,2009.

Research on Forecasting the Fuzzy Boundary of VMG of Sailboat

Gao Hui, Pan Mingjie, Zhou Xiang, Ren Jiuchun, Zhu Qian
(School of Information Science and Technology, Fudan University, Shanghai 200433, China)

VMG is the projection of sailboat speed in the direction of real wind during the process of sailing. It shows sailboats’ ability to sail against wind as well as athletes’ ability to make use of wind. Therefore, for the athletes, if they can master the trend of VMG, they could make much more scientific decisions for sailing direction. Based on the raw data of sailboat competition which is collected in the research project named Sailing Environmental Monitoring and Motion Analysis system development, this paper uses information granule based on fuzzy set to granulate the raw data to achieve fuzzy particles of VMG. Afterwards, it uses SVM (Support Vector Machine,SVM) to regress the upper and lower bounds of the fuzzy particles. Finally, we achieve the interval prediction of VMG fuzzy boundary of sailboats. Simulation results have approved the effectiveness of this method.

Velocity Made Good; Time Series Prediction; Support Vector Machine; Information Granule; Fuzzy Boundary

TP181

A

1007-757X(2014)07-0030-05

2014.04.25）

上海市科委攻关项目

高 慧（1989-），女，皖，复旦大学通信系，硕士研究生。研究方向：机器学习，无线传感网络，无线通信MIMO技术，上海 200433潘明杰（1990-），男，上海，复旦大学通信系，硕士，研究方向：无线传感网络，上海 200133周 翔（1991-），男，无锡，复旦大学通信系，研究生，研究方向：无线传感网络，上海，200133任久春（1974-），男，上海，复旦大学通信系，讲师，研究方向：通信网络，机器学习，研究方向：无线传感网络，上海 200133朱 谦（1960-），男，上海，复旦大学通信系，副教授，研究方向：无线传感网络，研究方向：无线传感网络，上海 200133