基于粒子群算法的计算机网络路由优化研究

张得生，李留青，陈萍

基于粒子群算法的计算机网络路由优化研究

张得生，李留青，陈萍

针对计算机网络规模日益扩大所带来的网络路由优化问题，将其数学本质规划为NP问题，提出使用粒子群优化算法求得路由优化的近似最优解。同时，为了提高粒子群算法的性能引入了变异机制，使粒子群算法的进化速度得到明显提升。仿真实验表明，提出的方法可以在较短时间内得到路由优化的结果，具有较好的有效性和实用性。

网络路由；粒子群算法；优化

0 引言

随着计算机技术、通信技术、微电子等技术的逐渐提高，以及互联网的逐渐普及，人们日常的生活越来越离不开计算机网络。在计算机网络给人们生活带来便利的同时，其优化问题也越来越突出。理想的路由选择策略能够大大降低网络的传输时延，提高传输的实时性，并降低网络的运营费用，增强对网络资源的合理有效利用。对于计算机网络来说，优化问题其实就是一类特殊的组合优化问题。而计算机网络的路由优化正是属于NP-hard组合优化问题[1-2]。

NP-hard组合优化问题是一类难以求解的组合最优化问题，人们从开始研究直到现在，还没有找到一个算法可以求得其最优解。但是这类问题的实际应用背景很强，所以，为了解决这个问题，通常都是假设这一类难解的组合优化问题不存在最优解，然后，用一些算法求得满足要求的次优解[3]。

传统的优化算法存在较大的缺点，其要求被优化对象的数学模型必须精确已知，这在实际应用中往往很难做到。而且，当模型较为复杂以及约束条件较多时，这些方法往往不能进行有效求解，或者即使能够求解但是算法复杂度过高，当模型维数较大时，会出现“组合爆炸”现象。随着NP-hard理论的建立和发展，人们开始尝试使用一些新的算法来优化计算机网络路由，包括神经网络、遗传算法等在内的一些方法都被使用[4-6]，取得了一定的效果。

根据现代计算机网络的特点，以及路由优化这个NP问题的特性，本文提出使用粒子群算法（Particle Swarm Optimization，PSO）来解决其优化问题。文中详细的给出了路由优化的数学模型，同时，为了解决PSO算法的早熟收敛问题，引入了变异机制。仿真实验表明，本文提出的优化方法效果较好，具有一定的实用性。

1 路由优化的数学模型

路由优化模型是一个NP完全的组合优化问题, 可以把它简化为这样一个问题：

已知条件：

① 网络的拓扑结构、节点集合及链路集合；

② 分布于网络中的每一个成对通信节点及其可能的路由集合；

③ 在传输过程中对于节点对的一些性能要求，同时要求链路容量已知。

问题是：每一个通信节点对都存在多个候选路由，而这些候选路由的性能对于网络的整体性能影响较大，如何从这些备选集合中选取一条最优路由，使得网络的传输性能最佳的同时网络平均时延最小。

中间节点位于分组交换网中，按照存储转发方式工作。其中，等待使用输出链路的时延最长，结点处理时延和链路传播时延较短，可以忽略不计。这种情况下，分组交换网就等同于一个M/M/1排队模型，也就是说报文处理时间可以看作是一个具有连续时间变化的负指数变量，同时可以用泊松过程来描述单队列情况下分组到达和发送的整个过程。因此，可以用式（1）来刻画某条链路l的报文分组（PL）的平均时延为公式（1）：

整个网络的平均时延是通过对所有链路时延进行加权求和得到，如公式（2）：

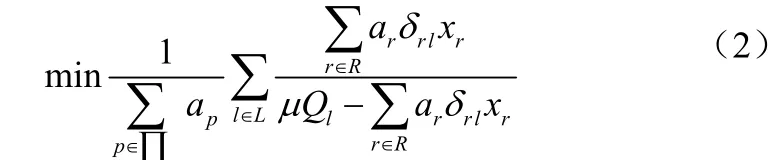
对于公式（2）需要考虑以下3个约束条件：

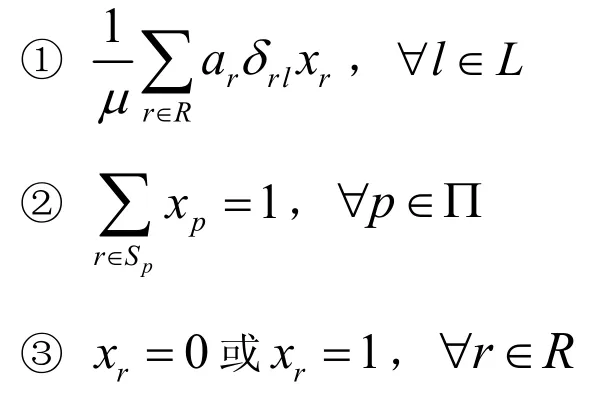
网络路由优化模型是一个多约束条件下的非线性0-1规划问题。设置约束条件①是为了保证链路的数据传输速率不超过链路容量；而约束条件②表明任一个通信节点对都有且仅有一条路由存在，以保证其通信需求；最后，约束条件③规定了决策变量问题的核心，即在满足上述条件下，使得目标函数值最小。

2 PSO算法及其改进

PSO算法是由J.Kennedy与R.Eberthart于1995年共同提出的一种仿生优化计算方法，其思想来源于人工生命和演化计算理论，最初的原型是模仿鸟群的捕食行为。该算法的计算过程为：首先，初始化一群代表最优解的粒子，但要注意由于其是潜在的解，因此，必须在可能求解的范围内进行初始化。这些初始化的粒子具有3个性能指标，分别为位置、速度和适应度。其中，适应度的值直接反映粒子性能的好坏，所以，适应度函数的正确选取十分重要。求解的过程可看作是粒子的一个运动过程，每一个粒子个体的位置在求解过程中都要不断更新，主要是依据个体极值Pbest和群体极值Gbest。粒子更新了一次位置以后，需要重新计算此时的适应度值，其目的是与Pbest和Gbest的适应度值进行比较，根据优劣程度进行更新[8]。

粒子的速度和位置在每一次迭代过程中都需要不断更新，更新公式为公式（3）、（4）：

容易早熟收敛是PSO算法存在的一个不可忽视的缺陷。针对这一问题，本文参考GE算法中的变异操作，在PSO算法中引入这种机制，即设定一个适合的概率，按照这个概率对某些变量重新初始化。在PSO算法中引入变异机制以后，可以有效的使种群搜索空间得到扩展，这样粒子便不会仅局限于原来的最优值位置，能够搜索更大的潜在解空间，同时保持了种群多样性。但是，本文引入的并不是普通的简单变异算子，而是使用参考文献[9]中的Sigmoid形式变异算子，具体形式如公式（5）：

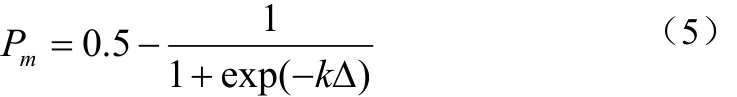
3 利用PSO算法进行网络路由优化的实现步骤

首先，根据计算机网络的规模和拓扑结构，确定网络中变量的个数。然后，将这些变量设定为PSO算法所需要的粒子，同时，根据式(2)计算粒子适应度值，接下来进行个体和群体寻优迭代。粒子速度和位置按照公式（3）和（4）进行更新，具体的算法实现流程如图1所示：

图1 算法流程图

4 仿真实验

本文所采用的实验仿真对象是Matlab自带数据集中的USA Network，其网络拓扑结构如图2所示：

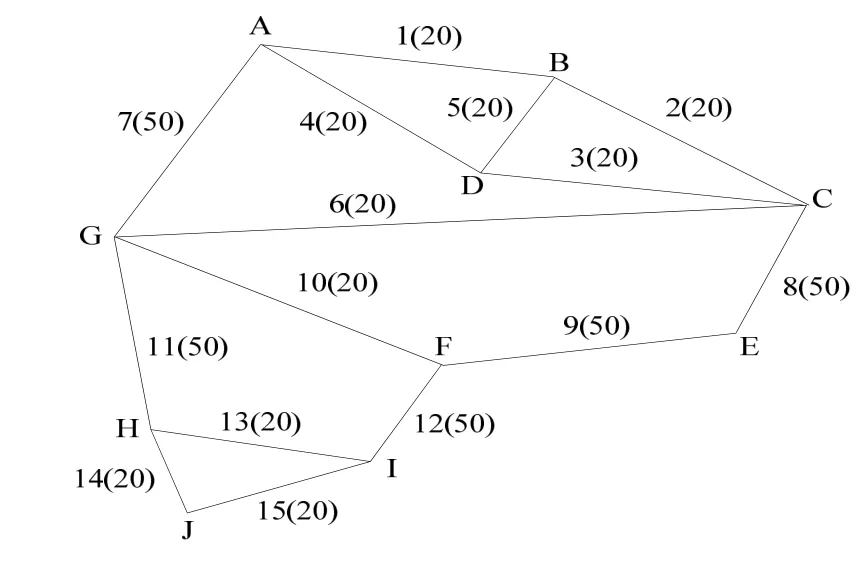
图2 USA Network 拓扑结构

该网络具有10个结点，15条链路，每条链路上标有链路编号及链路容量(kbit/s)。用表示节点对之间的通信量，并且假定节点对与节点对之间的通信线路和链路容量完全相同。平均报文长度为优化目标为：优选出各节点对之间的最佳通信路由，使得网络平均时延达到最小。

为了利用PSO算法优选出最佳的路由方案，首先，分析图2中的网络结构，可以确定这是一个具有20个变量和25个约束条件的非线性0-1规划问题。为了进一步计算，下面给出通信量和候选路由矩阵，如表1所示：

表1 通信量和候选路由矩阵

仿真时设定种群粒子数为20，每个粒子的维数为20，算法迭代进化次数为100。首先比较一下引入变异机制以后PSO算法性能的提升，如图3所示：

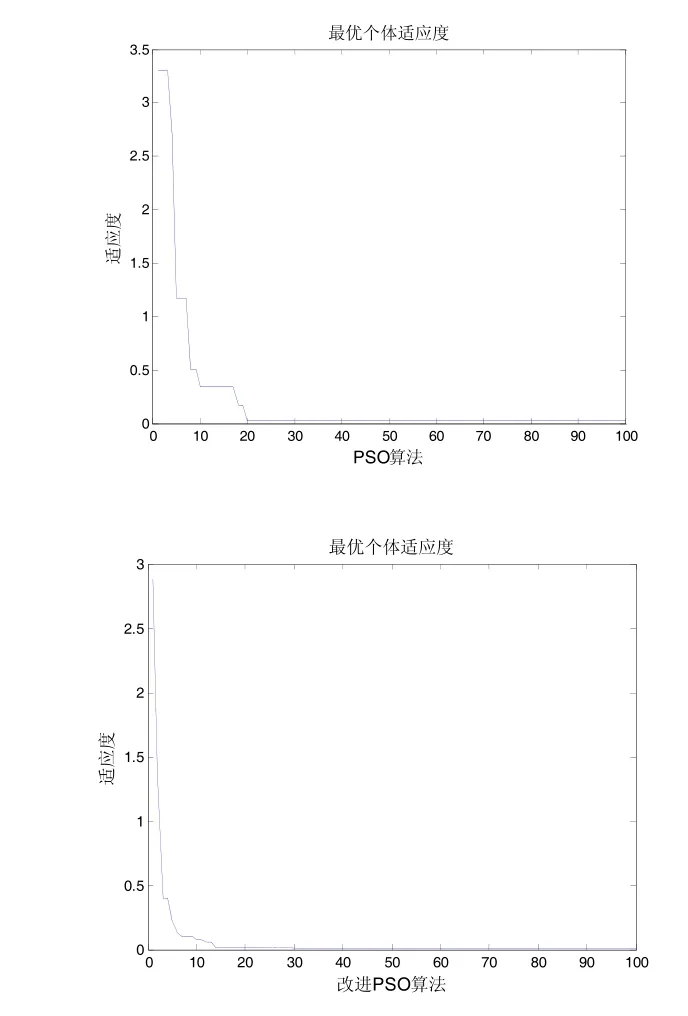
图3 最优个体适应度值进化对比

可见改进后的PSO算法，其适应度的进化速度得到明显提升。网络路由的优化结果为：通信路径最优解为即使用传统PSO算法时，最小时延为0.089570s；改进PSO算法得到的为0.089269s。这个实验结果表明，PSO算法可以比较有效的解决网络路由优化问题，具有较好的全局寻优能力。

为了进一步全面比较本文提出的改进PSO算法与传统PSO算法在处理网络路由优化问题时的性能，本文又选取了Matlab软件标准网络测试数据集中的共20个网络，其中包括3个中型网络，分别为NASA Network、Mini Pacific Ocean Network以及Central bank Network。在软硬件环境和测试数据集都一致的情况下，两种算法的平均最小时延如图4所示：

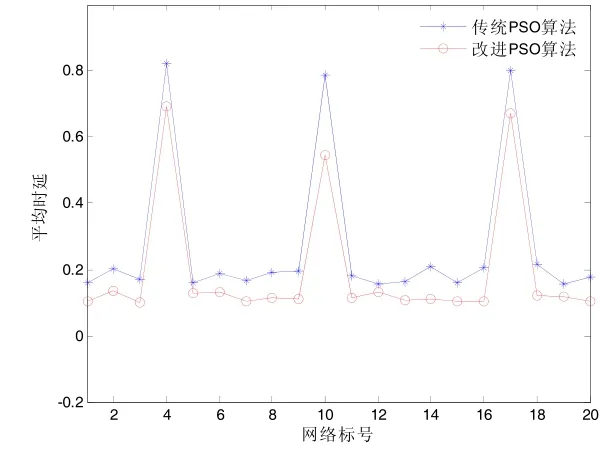
图4 传统PSO算法与改进PSO算法性能对比

从图4中可以明显看出，改进后的PSO算法在处理网络路由优化问题时，明显网络平均时延要小于传统PSO算法。尤其是在第4、10和17位置，分别是3个中型结构网络，传统PSO算法的时延分别为0.823，0.787，0.801，而改进后的PSO算法时延仅为0.694，0.547，0.673，工作效率明显要更优。而在可以得到同样结果的情况下，工作效率的明显提升具有非常重要的工程实践意义。因此，本文提出的改进PSO算法不仅可以正确的得到网络路由的最终优化结果，而且可以获得更为少的网络时延。

5 总结

网络路由优化一直是计算机网络管理中的一个重要问题。本文根据其数学模型的本质，将其作为NP规划问题处理。采用PSO智能算法解决其路径寻优，并引入变异机制改善传统PSO方法的不足。仿真实验表明，本文提出的这种方案可以较好的解决基于时延的动态路由选择问题，算法简单，适时性高，能够获得全局近似最优解，使得在网络的管理过程中可以根据计算结果进行动态路由选择和最佳流量分配，以达到控制网络时延的目的。

[1] 寇增涛. 计算机网络路由研究概述[J]. 计算机光盘软件与应用, 2012, 10(10): 59-61.

[2] 马伟. 计算机网络路由探究综述[J]. 电子测试, 2013, 13(7): 250-251.

[3] 王锡智. 计算机网络路由技术研究综述[J]. 煤炭技术, 2013, 32(7): 160-162.

[4] 孔玉静, 侯鑫, 华尔天等. 基于BP神经网络的无线传感器网络路由协议的研究[J]. 传感技术学报, 2013, 26(2): 246-250.

[5] 孙力娟, 吴新余. 应用遗传算法求解计算机通信网的最佳路由: —种新的遍历匹配选择算法[J].南京邮电学院报, 1996, 16(2): 16-21.

[6] 李晓磊, 邵之江, 钱积新.一种基于动物自治体的寻优模式: 鱼群算法[J].系统工程理论与实践, 2002.22(11): 32-28.

[7] 李祖鹏, 黄建华, 唐辉. 基于P2P计算模式的自组织网络路由模型[J]. 软件学报, 2005, 16(5): 916-931.

[8] 纪震, 廖惠连. 粒子群算法及应用[M].北京：科学出版社，2009.

[9] 吴浩扬, 朱长纯, 常炳围等. 基于种群过早收敛程度定量分析的改进自适应遗传算法[J]. 西安交通大学学报, 1999, 33(11): 27-30.

Research on Optimization of Computer Network Routing Based on Particle Swarm Optimization Algorithm

Zhang Desheng, Li Liuqing, Chen Ping
(School of Information Engineering, Huanghuai University, Zhumadian 463000, China)

The network routing optimization problem is increasingly evident with the growing scale of computer network. In order to solve this problem, which the mathematical essence is the NP problem, the method of using particle swarm algorithm to obtain approximate optimal solution is proposed. Meanwhile, in order to improve the performance of PSO, mutation mechanism is introduced, so that the speed of evolution particle swarm algorithm has been significantly improved. Simulation results show that the proposed method can be obtain route optimization results in a relatively short period of time, and it has relatively effectiveness and practicality.

Network Routing; PSO Algorithm; Optimistic

TP393.02

A

1007-757X(2014)07-0022-04

2014.06.15）

河南省教育厅科技攻关项目（No.13A520786）；河南省科技攻关项目（No.122102210510）

张得生（1982-），男，黄淮学院，实验师，硕士，研究方向：计算机应用，驻马店 463000李留青（1981-），女，黄淮学院，讲师，硕士，研究方向：计算机应用，驻马店 463000陈 萍（1969-），女，黄淮学院，教授，硕士，研究方向：计算机网络及信息安全，驻马店 463000