新扩展多变量公钥密码方案

乔帅庭，李益发，韩文报

（1.信息工程大学 四院，河南 郑州 450002；2. 数学工程与先进计算国家重点实验室，江苏 无锡 214125）

1 引言

二十一世纪是信息的时代，继电子信息科学技术之后，量子和生物等新型信息科学正在建立和发展。量子计算机的产生将会对目前广泛使用的基于离散对数（包括椭圆曲线上的离散对数）和大数分解的公钥密码体制构成潜在的威胁[1～3]。为此，基于抗量子的公钥密码体制成为密码学中一个研究的热点和重点[4]。多变量公钥密码系统作为一种能有效抵抗未来的基于量子计算机攻击方法的密码体制，在近二十几年受到越来越多的关注。

多变量公钥密码体制的安全性是基于有限域上多元非线性方程组的难解性[5]和多项式同构问题[6]。1988年，日本学者Matsumoto和Imai提出了第一个多变量公钥密码方案，即著名的Matsumoto-Imai(MI)方案[7]。该方案将“小域—大域”思想引入了多变量公钥密码方案，有较高的计算效率，在当时被认为是安全的。然而，1995年，Patarin等提出了针对MI方案的线性攻击[8]，攻破了原始的MI体制。为了抵抗线性攻击，Patarin等在2001年提出了FLASH方案[9]，Ding等人于2004年提出了PMI方案[10]，但都受到差分攻击的影响[11,12]。到目前为止，多变量公钥密码体制主要有5类方案[5]：MI方案、hidden field equation (HFE)方案、unbalanced oil andvinegar (UOV)方案、stepwise triangular systems (STS)方案和medium field equation (MFE)方案，但大部分不能同时用于加密和签名。近几年来，多变量公钥密码体制的研究一直是热点，相继出现了CyclicRainbow方案[13]、Double-Layer square方案[14]、Enhenced STS方案[15]等，它们在安全性上得到了不同程度的提高[16,17]。2011年，Wang等通过引入Hash认证技术、并结合传统Multivariate Quadratic（MQ）公钥密码算法，提出了一种扩展MQ公钥密码体制[18]，同时具备加密和签名功能。但该方案的加密和签名算法的构造较为复杂，引入了较大的私钥空间。本文利用函数合成思想，构造了一种独特的基于温顺变换思想[19]的非线性可逆变换，并将此变换与MI方案结合起来，提出了一种新的扩展多变量公钥密码方案，且给出了新的扩展方案的加密和签名方案。分析结果显示：该方案继承了MI方案计算高效的特点，具有较小的私钥量；克服了MI方案不能抵抗线性攻击、差分攻击的缺陷，还能抵抗代数攻击。

2 多变量公钥密码体制及MI方案简介

本文方案是在多变量公钥密码体制基础上，与MI方案结合而成的，下面从多变量公钥密码体制的一般结构、加解密及签名和MI方案三方面对相关研究工作展开论述。

2.1 多变量公钥密码的一般结构

多变量公钥密码的门限函数形式为有限域上一类多元二次方程组

每个pi为一个关于x=(x1,…,xn)的非线性二次方程

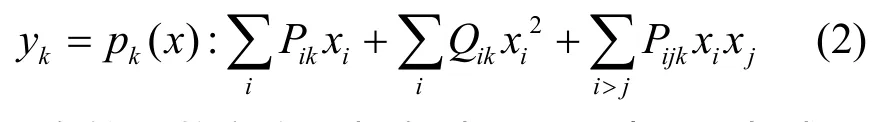
所有的系数和变量都在域K=Fq中，q为域K的阶。多变量公钥体制的构造主要基于multivariate quadratic (MQ)问题及isomorphism of polynomials(IP)问题的难解性。

定义1 给定有限域Fq上的n个变元m个方程组成的非线性方程组

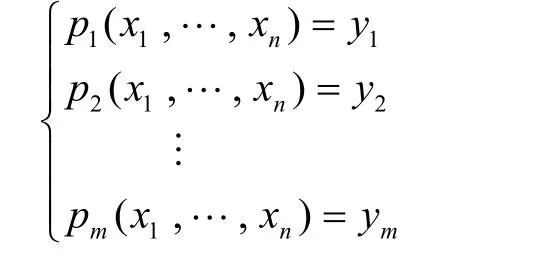
其中，pi的系数和变量均取自有限域K=Fq，通常q＞2，每个多项式的形式为

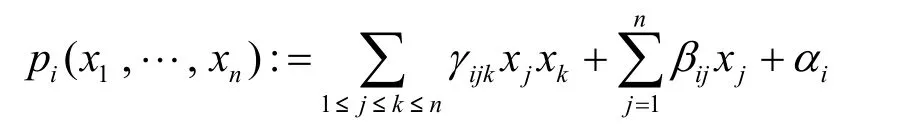
求解该方程组的问题称为MQ问题。已经证明MQ问题为NP难问题，即使是在最小的域F2上。

定义2 设(P)和(Q)为有限域Fq上随机的n元m个方程的多变量方程组，且(P)和(Q)同构，则有P=T◦Q◦S ，T和S分别为2个可逆的仿射变换。称寻找从(Q)到(P)同构的(T, S)的问题为IP问题，即多项式同构问题。

一般地，设(Q)∈(Fq[a1,…,an])m为Fq上m个多项式集合，集合中每个多项式都是n元二次多项式，其形式如下

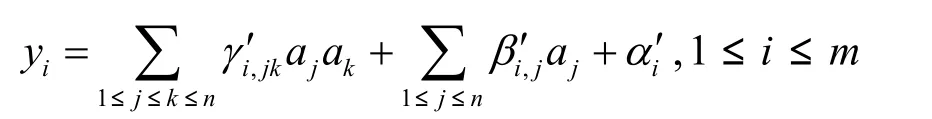
2.2 加解密及签名

多变量公钥密码的加解密方法如下所示

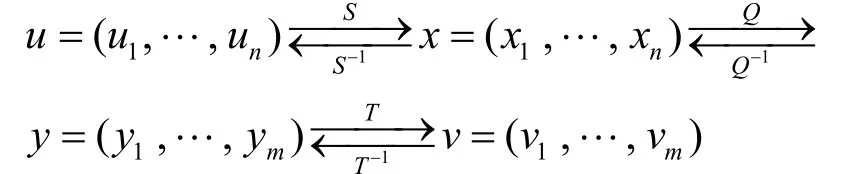
这里，S和T分别为Fqn和Fqm上的可逆仿射变换，中心映射为Q:Fqn→Fqm，公钥为P=T◦Q◦S，S和T共同“隐藏”中心映射Q的结构，是私钥的重要组成部分。

1) 加密

给定明文(u1,…,un)，利用公钥P=T◦Q◦S对其进行运算，得到密文(v1,…,vn)=P(u1,…,un)。

2) 解密

给定密文(v1,…,vn)，利用私钥{T-1, Q-1, S-1}对密文依次进行T-1、Q-1和S-1运算，得到明文

3) 签名

给定消息M，得到消息摘要(v1,…,vm)=Hash(M)，利用私钥{T-1, Q-1, S-1}对其依次进行T-1、Q-1和S-1运算，得到签名

4) 验证

给定签名(u1,…,un)，利用公钥P=T◦Q◦S对其进行运算，得到消息摘要(v1′,…,vm′)，然后判断(v1′,…,vm′)=Hash(M)是否成立，若成立，则签名有效，否则，签名无效。

2.3 MI方案

1988年，Matsumoto和Imai提出了第一个多变量公钥方案——MI方案[7]。

令k为一有限域，k=Fq，特征为2，可设q=2w。K为k的n次扩域，K=Fqn。 定义K同构φ：K→kn，正整数 θ满足gcd(1+qθ, qn-1)=1，此时定义F：K→K，F(X)=X1+qθ，则F为可逆的，F-1(X)=Xt，这里t满足t(1+qθ)≡1 mod (qn-1)。

最后，随机选择2个kn上的可逆的仿射变换L1和L2，定义

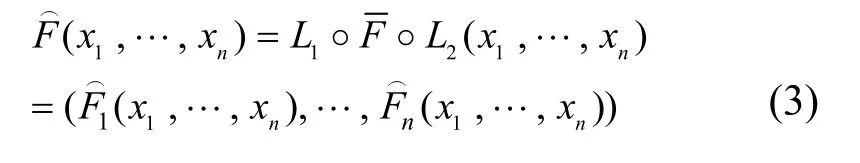
3 新的扩展多变量公钥密码方案

多变量公钥密码体制根据不同的中心映射的构造方法主要可分为：MI体制、隐藏域方程体制、不平衡油醋体制、三角形体制以及中间域方程体制。这些算法大多不能同时用于加密和签名，而且，大部分受到不同程度地攻击[19]，例如线性攻击、差分攻击、代数攻击等。如何构造一种安全高效且同时具备加密和签名功能的多变量方案仍是一个值得研究的难题和热点。

本文利用温顺变换(tame transformation)思想，构造出非线性可逆变换L3:Fqn→Fqn，即L3(x1,…,xn)=(t1,…,tn)。然后，将MI方案与基于温顺变换思想的非线性可逆变换结合起来，提出了一种新的扩展多变量公钥密码方案

3.1 L3的构造

L3的构造用到一类特殊的映射G:GF(q)n→其形式为

其中，gi为任意二次多项式。此变换结构特殊，容易求逆，也称温顺变换[19]。

取正整数n，d，且满足n＞2d，构造基于温顺变换的可逆变换L3(x1,…,xn)=(t1,…,tn)，其形式如下

3.2 新扩展方案

利用函数合成思想将MI方案与基于温顺变换思想构造的L3结合，得到新扩展多变量公钥密码方案的公钥多项式为

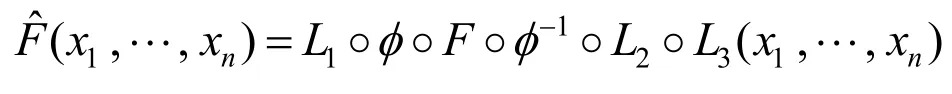
其中，L1、L2、φ、φ-1的定义同MI方案中的定义一致，L3的定义如3.1节所述。正整数θ满足条件gcd(1+qθ,qn-1)=1，此时定义F：K→K，F(X)=X1+qθ，则F为可逆的，且当t(1+qθ)≡ 1 mod (qn-1)时F-1(X)=Xt。

3.3 基于新扩展体制的加密方案

加密过程：加密者用公钥Fˆ对明文(x1,…,xn)进行加密，得到密文：

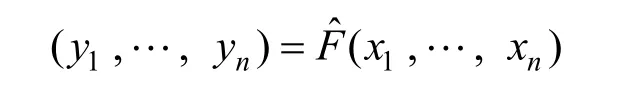
解密过程：解密者收到密文(y1,…,yn)后，做如下计算。

1) 用私钥L1-1计算可得

3) 用私钥L2-1计算得到

4) 用私钥L3-1计算便可得到相应的明文

由解密的过程，可得明文(x1,…,xn)与密文(y1,…,yn)满足如下关系式：

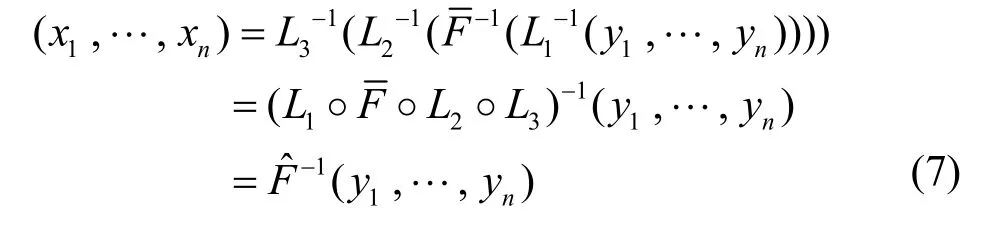
3.4 基于新扩展体制的签名方案

签名：设M为待签名文件，用公开的散列函数Hash计算(y1,…,yn)=Hash(M)。签名体制的私钥和上述加密方案的私钥一致，计算签名(x1,…,xn)的步骤和3.3中解密步骤相同，不再详述。

验证：验证者收到消息M和签名(x1,…,xn)后，验证如下。

1) 计算Hash(M)=(y1,…,yn)；

2) 然后验证下列方程组是否成立。若成立，则签名有效；否则，签名无效。

4 新方案的性能分析和安全性分析

下面将对新方案进行性能分析和安全性分析。性能分析主要包括公私钥大小和扩展体制的运算效率。安全性分析则从针对多变量公钥密码体制的结构攻击和直接攻击着手。

4.1 性能分析

4.1.1 公私钥大小

1) 基于“温顺变换”思想的扩展方案的公钥的一般形式为

由3.1节中it的构造可得

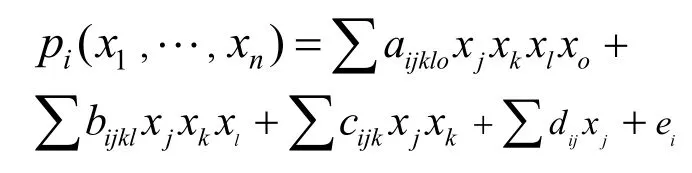
对于私钥而言，如3.1节定义，L3的私钥为c1,…,cd，由于d=6，相对于L1、L2的私钥量，L3的私钥量极小，而MI方案的私钥量大小约为2wn2bit，Wang等人的方案私钥量约为3wn2bit，新扩展方案的私钥量大小约为w(2n2+6) bit，在推荐参数w=8，n=32下，MI方案私钥量大约为2 KB，Wang等人的私钥量约为3 KB，新扩展方案的私钥量约为2 KB，与MI方案相比，对应的扩展体制私钥量基本不发生变化；与Wang等人的方案相比，本文新的扩展方案缩小了约1/3私钥量。

4.1.2 运算效率

由L3，L3-1构造可知，它们的运算仅仅多出了d个乘法和加法，在推荐参数w=8，n=32，d=6下，相对于MI体制的加解密和签名效率，运算L3和L3-1可忽略不计，不影响全局运算效率，因此，新的扩展体制保持了MI方案的高效性。

可见，本文提出的新的扩展方案具备较小的公钥量和私钥量，保持了MI方案的优势，具有较高的加解密和签名效率。

4.2 安全性分析

多变量体制的安全性分析分为结构攻击和直接攻击2类。结构攻击是针对多变量体制特殊的结构特征，主要包括线性攻击和差分攻击。直接攻击是从多变量体制的公钥多项式入手，常用的攻击方法为Gr˙obner基算法和XL算法。通常认为只要攻击方案的复杂度超过O(280)，则称该方案可抗此种攻击。下面进行本文方案的安全性分析。

4.2.1 抗线性攻击

1998年Patarin提出的一种线性攻击[8]，在w=8，n=32的情况下，经过O(232)次运算就可以求解。

根据MI方案特殊的中心映射F:X↦Xqθ+1，存在如下特殊的代数关系式

两边分别乘以XY，得到关系式

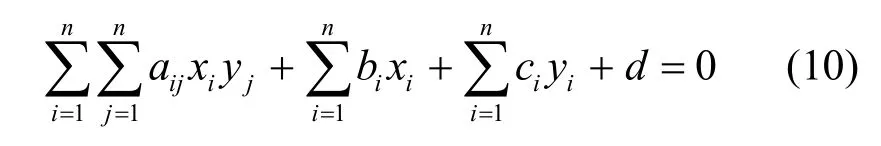
其中，aij、bi、ci、d为方程式的(n+1)2个系数。

在给出O((n+1)2)个明密文对(x1,…,xn,y1,…,yn)时，可以求解上述方程组的系数。一旦所有的系数均被求解得到，那么在给定密文y=(y1,…,yn)的情况下，就可得到关于明文x=(x1,…,xn)的n个线性方程组。

定理1 新扩展方案利用函数合成思想，将非线性可逆变换L3与MI方案结合起来，从而可抗线性攻击。

证明 根据中心映射的构造可得

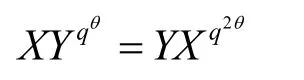
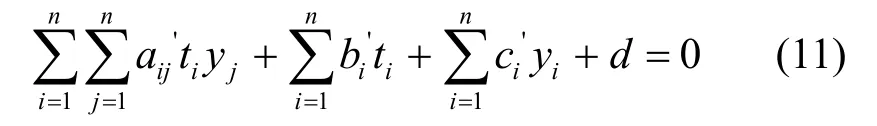
在给出O((n+1)2)个(t1,…,tn,y1,…,yn)时，可以求解上述方程组的系数。而密文(y1,…,yn)已知，中间量(t1,…,tn)未知，所以代入密文后仍然无法解出方程组的系数；但当d=1,…,5时，含有二次非线性项较少，此时若对t1,…,t5进行穷举，可以在O(280)时间以内攻破。以d=1为例，此时t1=x1-c1xd+1xn,ti=xi(i=2,…,n)得到如下的关系式

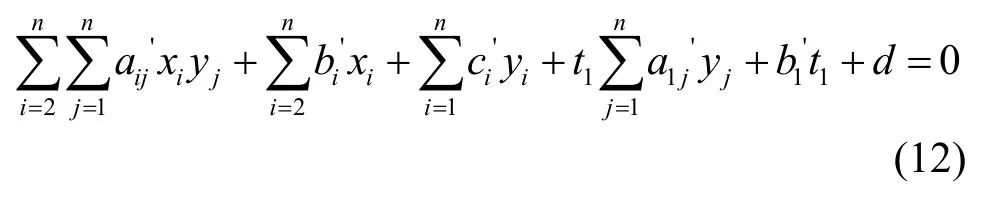
若对t1进行穷举，可得

而在参数w=8，n=32，d=1时，假设出现最好的情况：攻击者知道ti=xi(i=2,…,n)。在已知足够多的明密文对(t1,x2,…,xn,y1,…,yn)时，可求解出系数，在给定密文y=(y1,…,yn)时，可依次给出t1,x2,…,xn，此过程的复杂度为O(232)。再对c1穷举，可得到明文x1,…,xn，所以在d=1时，线性攻击成功的复杂度约为O(240)，当d=2时，线性攻击成功的复杂度约为O(248)，依次类推，d=5时，线性攻击成功的复杂度约为O(272)。所以当d≥6时，线性攻击成功的复杂度为O(280)，即安全级别为O(280)。

综上所述，新的扩展方案可抵抗线性攻击。

4.2.2 抗差分攻击

MI体制是公钥密码发展的一个里程碑，它为该领域带来了一种全新的设计思想。在此基础上，相继提出了PMI方案、SFLASH方案等。但是PMI方案、SFLASH方案均受到差分攻击。SFLASH方案其实就是MI-Minus方案即C*-体制，可通过差分分析恢复出r个被去掉的多项式的等价多项式，再加上已知的n-r个公钥多项式，从而构成了一个完整的MI方案的公钥多项式，这样就可重新利用线性攻击去伪造签名。

首先，给出差分的定义：对于函数()Fx，定义其在a点处的差分为

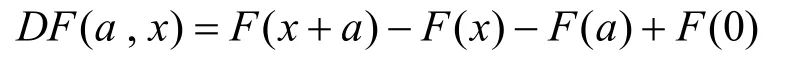
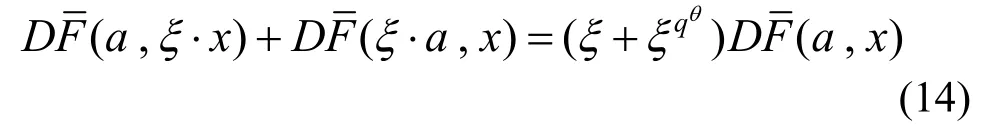
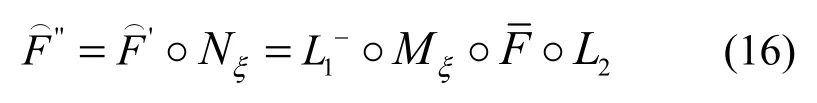
其中，Nξ和Mξ均表示关于ξ的线性映射。

定理2 新扩展方案在MI方案的基础上，引入了非线性可逆变换L3，打破了MI体制的乘法反对称性，能很好地抵抗差分攻击。

由于L3变换是一个非线性变换，对应地，式(17)中也是一个非线性变换，因此对于∀x,ξ∈GF(qn)，显然有

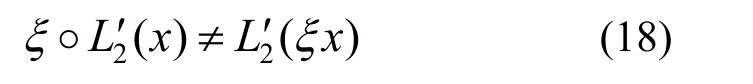
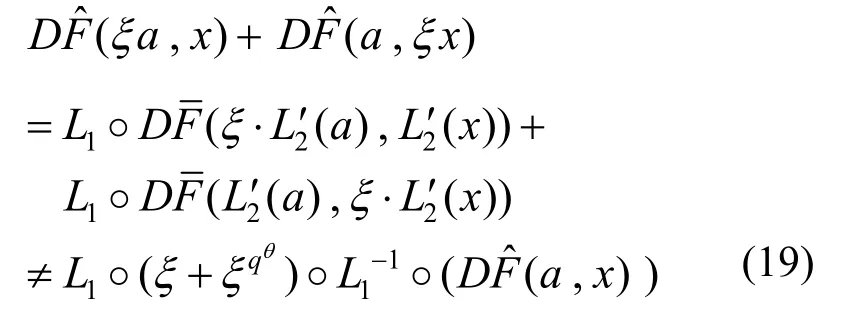
式(19)表明非线性变换L3的引入破坏了MI体制公钥的乘法反对称性。

所以新扩展方案能抵抗差分攻击。

4.2.3 抗代数攻击

代数攻击常用的工具包括Gr˙obner基算法和XL算法[17]。目前，计算Gr˙obner基最有效的算法为F4和F5算法。

证明 根据方程的个数m和变量的个数n之间的大小关系，分3种情况讨论。

1) 当m=n时，多元二次方程组为置换方程组，当k=GF(q)≠GF (2)时，求解方程组的复杂度为O(23m)[19]。

2) 当m＞n时，多元二次方程组为超定方程组，此时用XL算法。当m≥εn2，0＜ε≤1/2时，XL算法都可以在nO(1/ε)的多项式时间内运行成功[20]。

3) 当m＜n时，多元二次方程组为不定方程组[21]，求解的复杂度约等于穷尽搜索的复杂度O(qm)。

在新方案中，公钥多项式为P(x1,…,xn)=(p1(x1,…,xn),…,pn(x1,…,xn))，对应的方程组为

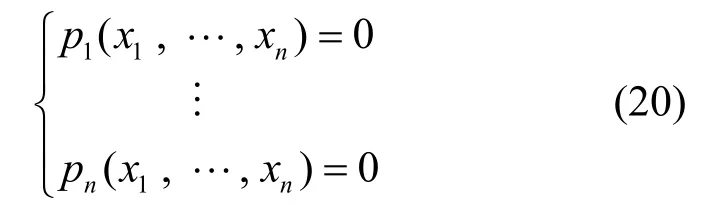
此时，方程组的个数和变量的个数相等，都为n，但由4.1.1节知pi(x1,…,xn)为多元四次多项式，求解方程组(20)的复杂度远大于求解多元二次方程组。在给定的参数n=32下，由情况1)可得，求解多元二次方程组的复杂度为O(296)，可见求解新体制公钥多项式的复杂度在O(296)之上。

所以新扩展方案在特定参数下可以抵抗代数攻击。

目前，针对多变量体制的攻击主要包括线性攻击、差分攻击和代数攻击。由定理1～定理3可知，新的扩展方案能同时抵抗线性化攻击、差分攻击和代数攻击，所以新扩展方案是安全的。

5 结束语

针对MI方案不能抵抗线性攻击和差分攻击，本文基于温顺变换思想构造了一种的独特的非线性可逆变换，并将此非线性变换与MI方案结合，提出一种新的扩展多变量公钥密码方案。对应地，构造了新的扩展方案的加密方案和签名方案。新的扩展方案保持了MI方案计算高效的优点，具有较小的公私钥空间；同时能抵抗线性化攻击、差分攻击和代数攻击，在安全性上得到了提高。是否存在一个新的攻击方法有待进一步研究。

[1] SHOR P. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J]. SIAM Rev, 1999, 41(2):303–332.

[2] 付向群, 鲍皖苏, 周淳. Shor 整数分解量子算法的加速实现[J]. 科学通报, 2010, 4: 322-327.FU X Q, BAO W S, ZHOU C. Speeding up implementation for Shor’s factorization quantum[J]. Chinese Sci Bull, 2010, 4: 322-327.

[3] MYASNIKOV A D, USHAKOV A. Quantum algorithm for the discrete logarithm problem for matrices over finite group rings[EB/OL].https://eprint.iacr.org/2012/574.pdf, 2012.

[4] BERNSTEIN D J, BUCHMANN J, DAHMEN E. Post-Quantum Cryptography[M]. Berlin: Springer-Verlag, 2009.

[5] DING J T, YANG B Y. Multivariate Public Key Cryptography[M].Berlin: Springer-Verlag, 2009.

[6] TANG S, XU L. Proxy signature scheme based on isomorphisms of polynomials[A]. NSS 2012[C]. Fujian, China, 2012. 113-125.

[7] MATSUMOTO T, IMAI H. Public quadratic polynomial-tuples for efficient signature-verification and message-encryption[A]. Advances in Cryptology—EUROCRYPT’88[C]. Switzerland, 1988. 419-453.

[8] PATARIN J. Cryptanalysis of the Matsumoto and Imai public key scheme of Eurocrypt’88[A]. Advances in Cryptology—CRYPT0’95[C].Santa Barbara, California, USA, 1995. 248-261.

[9] PATARIN J, COURTOIS N, GOUBIN L. Flash, a fast multivariate signature algorithm[A]. Topics in Cryptology—CT-RSA 2001[C]. San Francisco, CA, USA, 2001. 298-307.

[10] DING J. A new variant of the Matsumoto-Imai cryptosystem through perturbation[A]. Public Key Cryptography–PKC 2004[C]. Singapore,2004. 305-318.

[11] DUBOIS V, FOUQUE P A, STERN J. Cryptanalysis of SFLASH with slightly modified parameters[A]. Advances in Cryptology- EUROCRYPT 2007[C]. Barcelona, Spain, 2007. 264-275.

[12] DING J, GOWER J E. Inoculating multivariate schemes against differential attacks[A]. Public Key Cryptography-PKC 2006[C]. New York,USA, 2006. 290-301.

[13] PETZOLDT A, BULYGIN S, BUCHMANN J. CyclicRainbow–a multivariate signature scheme with a partially cyclic public key[A]. Progress in Cryptology-INDOCRYPT 2010[C]. Hyderabad, India, 2010. 33-48.

[14] CLOUGH C L, DING J. Secure variants of the square encryption scheme[A]. Post-Quantum Cryptography[C]. Darmstadt, Germany,2010. 153-164.

[15] TSUJII S, GOTAISHI M, TADAKI K,etal. Proposal of a signature scheme based on STS trapdoor[A]. Post-quantum cryptography[C].Darmstadt, Germany, 2010. 201-217.

[16] THOMAE E, WOLF C. Roots of square: cryptanalysis of double-layer square and square+[A]. Post-Quantum Cryptography[C]. Taipei, China,2011. 83-97.

[17] THOMAE E, WOLF C. Cryptanalysis of enhanced TTS, STS and all its variants, or: why cross-terms are important[A]. Progress in Cryptology-AFRICACRYPT 2012[C]. Ifrance, Morocco, 2012. 188-202.

[18] WANG H Z, ZHANG H G. Extended multivariate public key cryptosystems with secure encryption function[J]. Science China Information Sciences, 2011, 54(6): 1161- 1171.

[19] 王后珍, 张焕国, 管海明等. 多变量代数理论及其在密码学中的应用[J]. 北京工业大学学报, 2010 , 5: 627-634.WANG H Z, ZHANG H G, GUAN H M, etal. Multivariate algebra theory and its application in cryptography[J]. Journal of Beijing University of Technology, 2010, 5: 627-634.

[20] ALBRECHT M R, CID C, FAUGÈRE J C, etal. On the relation between the MXL family of algorithms and Gröbner basis algorithms[J].Journal of Symbolic Computation, 2012, 47(8): 926-941.

[21] THOMAE E, WOLF C. Solving underdetermined systems of multivariate quadratic equations revisited[A]. PKC 2012[C]. Darmstadt, Germany, 2012. 156-171.