平行板间边界层流体速度计算及差异分析

常青林

（中国海洋石油总公司工程建设部）

平行板间边界层流体速度计算及差异分析

常青林

（中国海洋石油总公司工程建设部）

利用粘性流体相关理论并结合施利希廷平行管道边界层研究成果，推导出了水平放置的平板间边界层流体速度计算公式。在一定假设条件下利用斯托克斯定律对该公式进行了验算，并对差异产生原因进行了定性分析。结果表明，考虑边界层条件时流体速度分布规律与理想流体明显不同，考虑边界层条件时油滴的实际运移距离比理想状态计算出的运移距离长5%～7%，对除油效果有一定影响。因此在斜板除油器设计中应充分考虑这种情况的影响。

平行板；边界层流体速度；边界层厚度；差异分析

斜板除油设备在海洋平台生产水处理中多作为第一级处理装置，用于分离生产水中大于50μm以上的浮离油。其基本原理是“浅层沉淀”，又称“浅层理论”［1］，即在重力沉降器中放置若干个相互平行、间距相等的斜板以达到提高除油效率的目的。由于隔板本身也具有一定的厚度，随着板间距的减小，板数增多，对有效分离容积会有较大的影响［2］。通常在设计时均假设流体为理想层流流动，用斯托克斯定律计算待处理最小粒径油滴到达上板的时间，并假设油滴到达上板即能够被脱除。而根据粘性流体力学理论，流体流过两平板之间时，速度不是恒定的。在最初一段距离内，由于受到上下板之间的摩擦阻力，在板内形成一个薄的边界层；边界层沿程增大，最后在某个位置相交，此后为具有抛物线形式作泊肃叶流动。

在粘性流体理论中，平板间的理想层流速度与泊肃叶流动速度均有准确的解析解或近似解；而对于平板间边界层厚度、速度以及边界层内速度分布的研究文献较少。本文利用粘性流体相关理论结合施利希廷的上下平行的直流管道内边界层的研究成果，推导出了水平放置的平板间边界层流体速度计算公式。在一定假设条件下用斯托克斯定律对公式进行了验算，并定性分析了产生差异的原因。

1 基本理论

1.1 理想层流流动

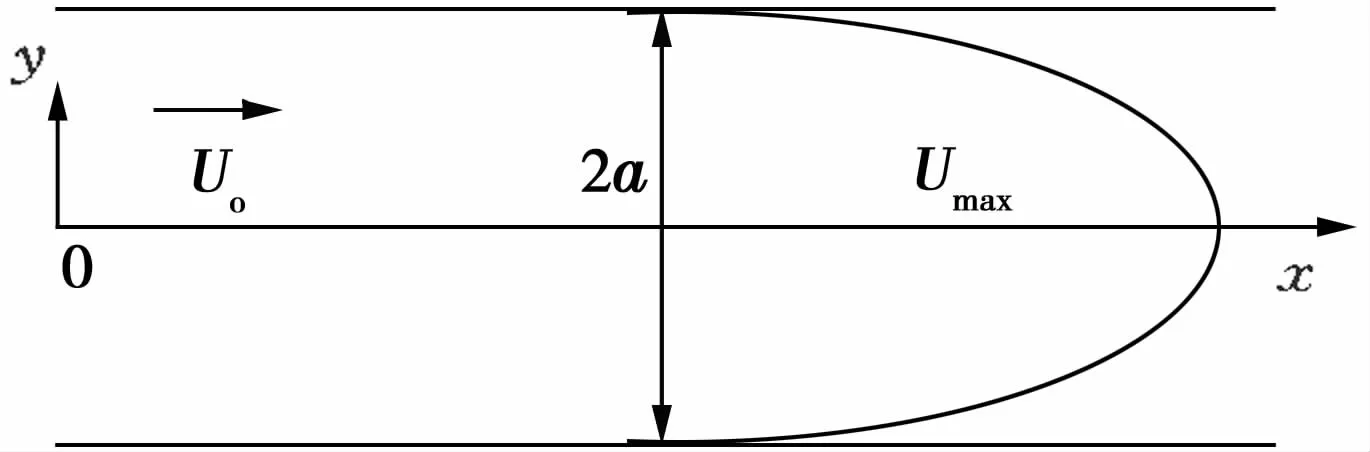
图1 平行板间流体流场示意图

流体在平行板间流动，其流场示意图见图1。设来流沿x轴方向平行匀速流动，速度为U0，y轴方向流体速度分量为0。假设介质是连续的，不考虑粘性的影响，流体在平板间各点流动都相同，这种流动为理想层流流动。油滴在层流状态下以平均速度上升，上升速度按斯托克斯定律计算

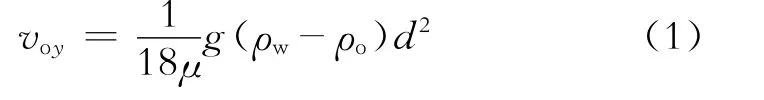
式（1）中：voy为油滴垂直浮升速度，m／s；μ为流体粘度，Pa·s；ρw和ρo分别为流体和油滴的密度，kg／m3；d为油滴直径，m。

油滴在x方向的流动速度等于流体的水平流速，即Uox＝U0。如果板长为L，板间距为2a，当粒径为d的油滴的速度小于时，油滴能够到达上板聚结被去除。

1.2 泊肃叶流动

在粘性流体力学中，将单纯由压力梯度引起的管或槽中流体的流动称为泊肃叶流动，是在流体进入管或槽后经过一定距离的流动达到稳定状态后形成的，可直接由纳维-斯托克斯方程得出解析解

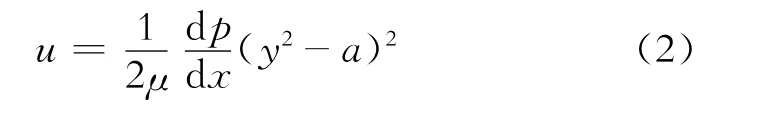
式（2）中：p为压强，边界条件为y＝a，u＝0；y＝－a，u＝0。在任意断面处的平均流速为

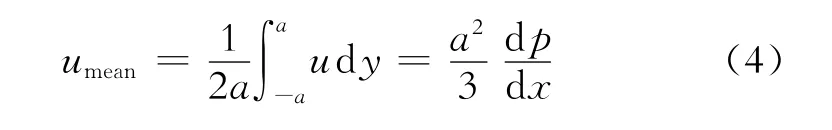
如初始速度已知，上式可进一步简化，并用最大流速umax表示为

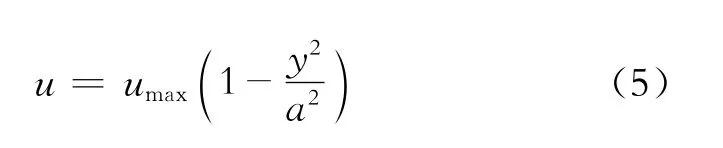
1.3 平板边界层

边界层是粘性流体中固壁面附近粘性起主导作用的薄层流体，在固壁面处速度为0，在很薄的厚度内速度沿法线方向迅速达到层外流体的速度。如果在流速为U0的流体中放置一块壁面光滑的平板，平板沿x方向无限长，则二维平面边界层微分方程式可写为

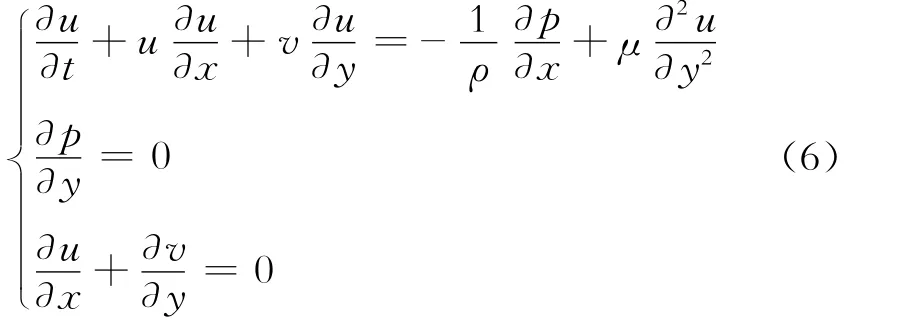
考虑边界条件（即y＝0，u＝0，v＝0；y＝∞，u＝U0），经过一系列计算，得出边界层厚度计算公式为

式（7）中：δ为边界层厚度，m；v为流体运动粘度，m2／s；K为系数。

边界层内外区域并没有严格的分界面，因此划分边界层的外缘具有一定的任意性；一般是通过人为约定在纵向的流速与层外流速uo相差1%的地方，即ux＝0.99 uo处作为边界层的外缘。由边界层外缘到物面的垂直距离定义为边界层的厚度［3］，不同的假设条件推导出的边界层厚度计算公式的系数不同。例如：朱克勤、许春晓［4］推导的近似解系数是3.464；章榟雄、曾图南［5］推导出的近似解系数为4.64；李玉柱、贺五洲［3］推导出的近似解系数为5.477。目前采用较多的是布拉修斯解，约等于5。分析认为，边界层公式在一定雷诺数Re范围内是适用的，计算与实验的结果也是吻合的；但如果x很小，或当Re小于100时，边界层理论则不能适用了，也就是说边界层在x＝0处是奇异的［6］。

由于边界层的存在，流体流速受壁面摩擦的阻滞而降低，使得在此区域内通过的流体流量较之理想流体流动时所能通过的流量减少，相当于固体壁面向内“移动”了一个小距离δ1，称为位移厚度。δ1≈也就是约为系数5的1／3。

1.4 二维管道进口段流体流动

假设管道进口断面处流体流速均匀分布，即流速为U0，由于粘性流动壁面的无滑移条件，上下壁面均将产生边界层流动，边界层将沿程发展［3］，交汇于管道半高度处。

施利希廷利用级数展开方法［7］计算出在上下管壁互相平行的二维直管道中上下边界层交汇于xc＝（见图2），在此断面后管道断面流速形成具有抛物线流速分布形式的泊肃叶流动；进口段长度Le＝0.04（2a）Re，此处Re为以板间距2a为特征长度的雷诺数。上述研究成果也被其他学者的研究所证实，但仅适用于“很大雷诺数”情况，对于小雷诺数也是不适用的［5］。

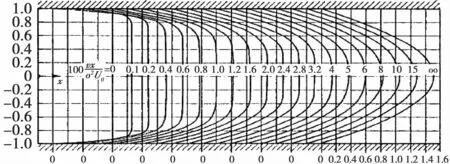
图2 二维管道进口段流体流动示意图

与平板边界层显著不同的是，由于壁面影响边界层内流体流速降低而损失的流量将由管道中心处流速增加得到补偿，上下壁面边界层流体流动是在外流为加速流的情况下发展的，任意截面处速度为常数，这部分流动称为势流核，从板前缘至xc处为进口段。边界层沿x轴逐渐增厚，到达平板半高度a处重合，势流核消失；此后变为具有抛物线形式的泊肃叶流动。

2 平板间边界层流体速度计算及假设条件

2.1 边界层流体速度计算

设流体质点在二维平行平板势流核内由x1移动到x2，根据上述理论和研究成果，可以得出Ux1＝常数1＜Ux2＝常数2，势流核沿程加速流动，至xc处速度增加到U。由式（4）和（5）式可知

平行平板间与一个平板上的边界层厚度取值有所不同。由于势流核内任意断面处流体速度为常数，在边界层上的速度就等于势流核内的流动速度。到达xc处形成泊肃叶流动时，势流核的速度达到最大，边界层速度也达到最大，且数值相等。因此，边界层速度可以不取外流速度的99%，边界层厚度也不再是人为选取的值，而是一个相对清晰的界线。

将平板间流体流动作为一个整体，根据质量守恒定律和不可压缩流体恒定总流的连续方程［2］，平板间各断面处流体流量应该相等。平板前缘处单宽流量q＝2aU0，设在进口段x处势流核速度为u（x），边界层厚度为δ（x），边界层上速度分布为ub（x），则在x断面处势流核内的单宽流量为

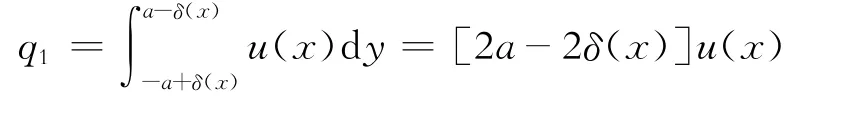
上下两板2个边界层内的流体单宽流量为

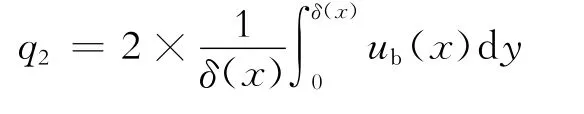
令q＝q1＋q2可得

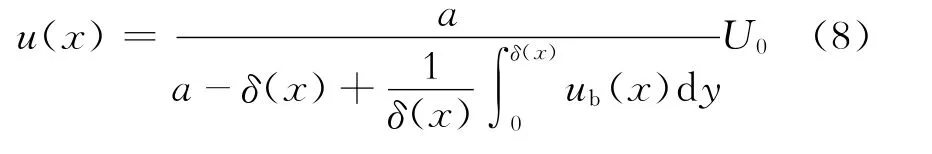
由于δ与v、U0及x有关，而v、U0是固定的，因此u（x）是■x的函数。

2.2 边界层厚度和边界层内流体速度分布的假设条件

由于泊肃叶流动的速度分布为抛物线形式，为使势流核内边界层内流体流速与泊肃叶流动的速度分布在xc处连续，假设其速度也是抛物线形式是比较合理的，可以保证在xc断面处用边界层速度分布公式和用泊肃叶流动速度分布公式计算的各点处流体速度相等。因此，设边界层内的速度分布

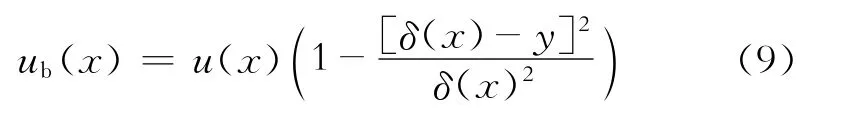
则在x处，2个边界层内的单宽流量为

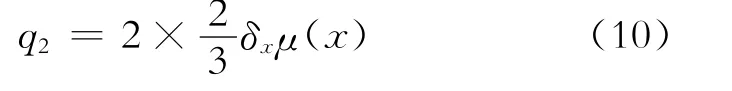
将式（10）代入式（8），得

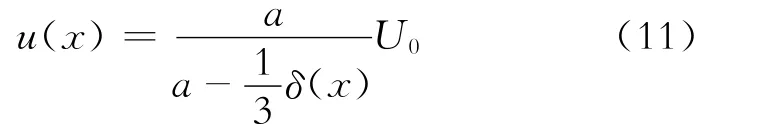
在上述假设条件下，原本在平板边界层内的流量损失则在2板间通过势流核和边界层内速度共同增加来补偿。

3 油滴在平板间运动轨迹的数值计算和差异分析

根据上述边界层速度计算公式以及边界层厚度和边界层内速度分布的假设条件，在保证流体流动为层流时可以用斯托克斯方程计算油滴在平板间的运动轨迹。在层流流动时，油滴在垂直方向匀速上升，在水平方向以与流体水平速度一样的速度位移，在流体中形成位移轨迹，可以用来比较平板间不同流态油滴在各处速度的分布情况。

3.1 油滴在板间运动轨迹的数值计算

计算模型选用长、宽各为1 m、板间距为0.03 m水平放置的两块平板；来流速度取0.01 m／s；运动粘度取常压50℃时的数值，0.556×10－6m2／s；水密度取999 kg／m3；油滴密度取900 kg／m3。以水力半径为特征值时，雷诺数2，小于层流临界雷诺数值500；以板长为特征值时，Re＝U0L＝v 1.8×104，可以满足流场层流和边界层层流状态条件（一般认为平板边界层保持层流的临界雷诺数为3.5×105～3.5×106）。

将图1中坐标原点移到下板前端。图3、4为油滴在平板间运动轨迹的数值计算结果，可以看出：计算边界层厚度的K值取2.5时，上下边界层相交于xc＝0.647 482 m处；K值取5时，上下边界层相交于xc＝0.161 871 m处（图3）。在0～0.647 482 m内为进口段，速度由0.01 m／s增加到0.015 m／s；沿进口段加速度则在板前缘突然增大，且随x增大迅速减小（理论上在xc处加速度应为0）；0.647 482～1 m区间内为泊肃叶流动。

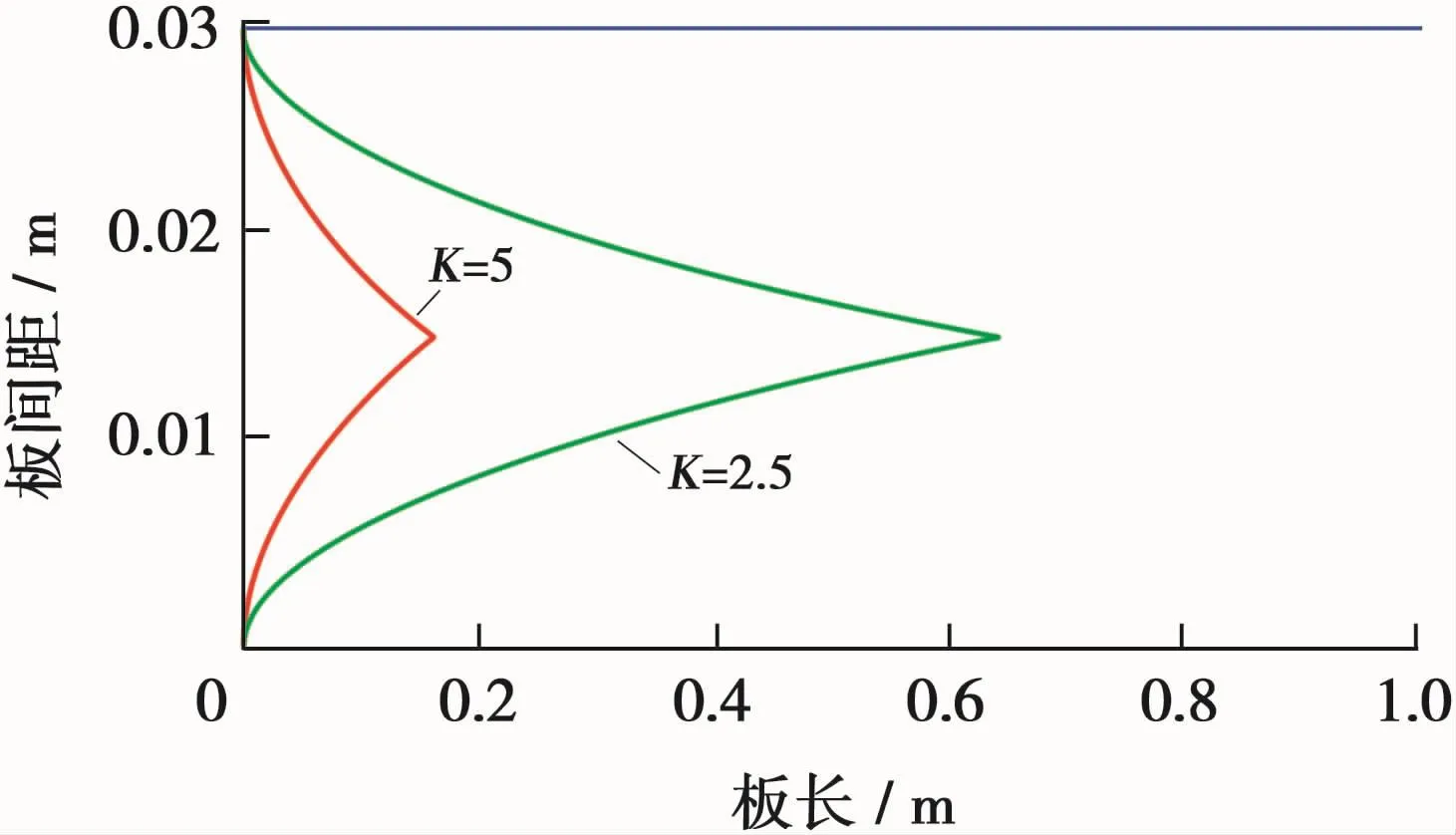
图3 不同板长及板间距时平板间边界层厚度曲线

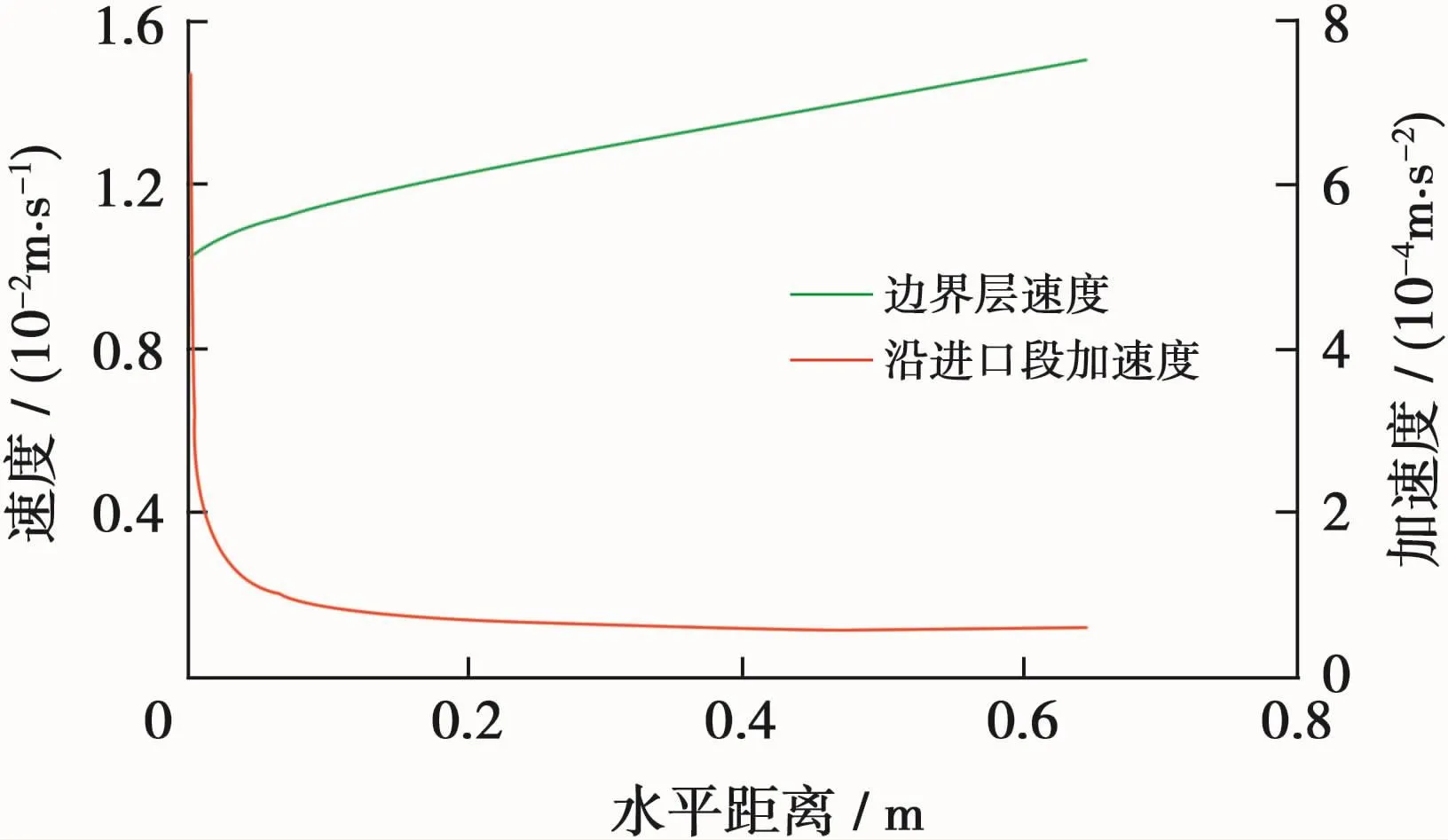
图4 平板间边界层流体的速度和加速度曲线

如图5所示，从原点出发的油滴在理想层流流动和泊肃叶流动时初始速度为0，到达上板的时间和水平移动距离都相同，只是运动轨迹不同。因此边界层条件下油滴到达上板的差异只与理想层流流动情况有关。

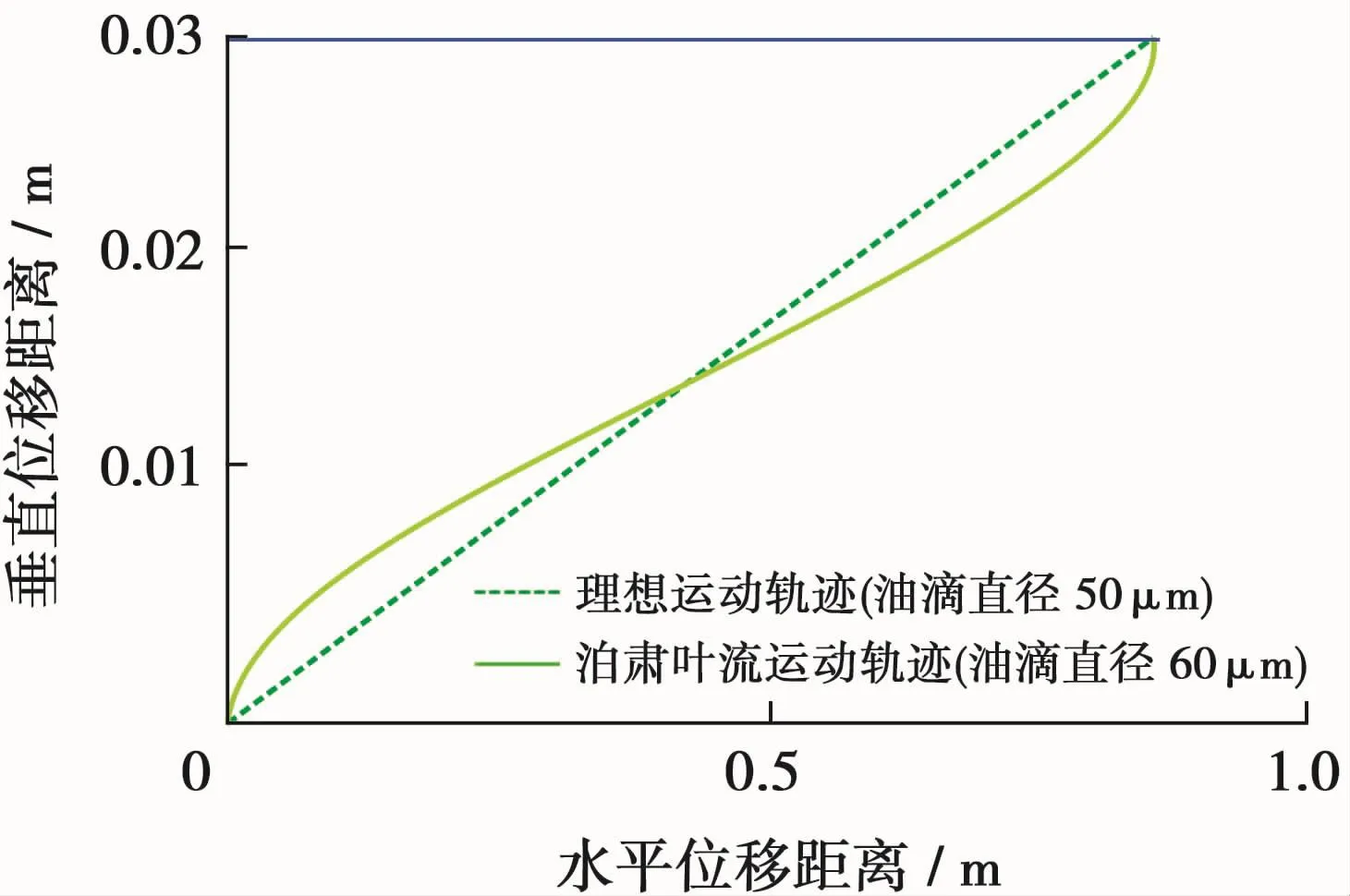
图5 平板间理想流动和泊肃叶流动油滴位移轨迹

选油滴粒径分别等于60、80、100μm计算油滴的位移轨迹，结果见图6。可以看出，边界层条件下，油滴到达上板的水平位移距离比理想状态下的位移距离要长，直径100、80μm油滴全部在进口段内位移，水平方向位移分别增加2.91%和3.37%；直径60μm油滴穿过进口段，在泊肃叶流动段内到达上板，水平位移距离增加5.92%。

3.2 差异分析

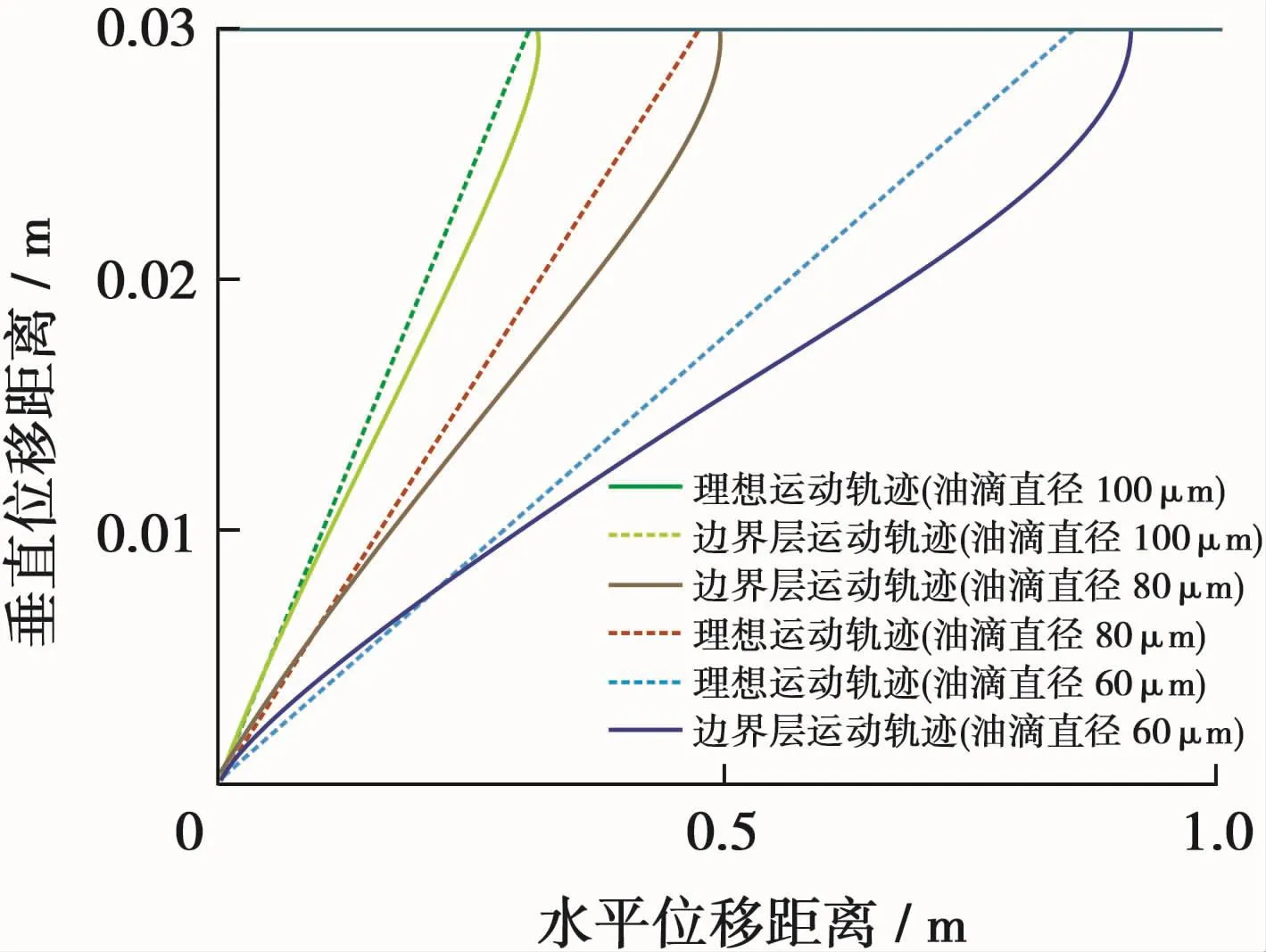
图6 平板间理想和边界层条件时油滴位移轨迹

为分析差异产生原因，可以通过调整参数人为将上下边界层交汇点延长至平板的末端。如果只增加来流速度至0.015 44 m／s，而其他参数保持不变时，直径60μm油滴在1 m距离内不能到达上板，直径100、80μm油滴水平位移距离分别增加2.91%和3.37%，与图6中算例中的差异一样，但水平位移距离的绝对值增加约6%（图7）；如果只降低运动粘度至0.36×10－6m2／s，其他参数保持不变时，3种粒径的油滴运动轨迹全部在势流核内（图8），100、80、60μm油滴水平位移距离分别增加1.16%、2.68%和2.97%。

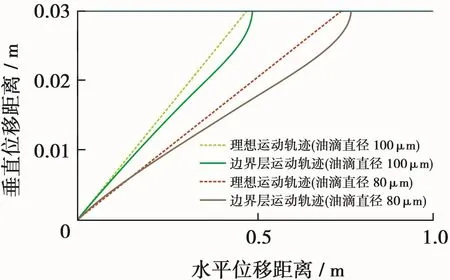
图7 平板间进口段流动油滴位移轨迹（初始速度为0.015 44 m／s）

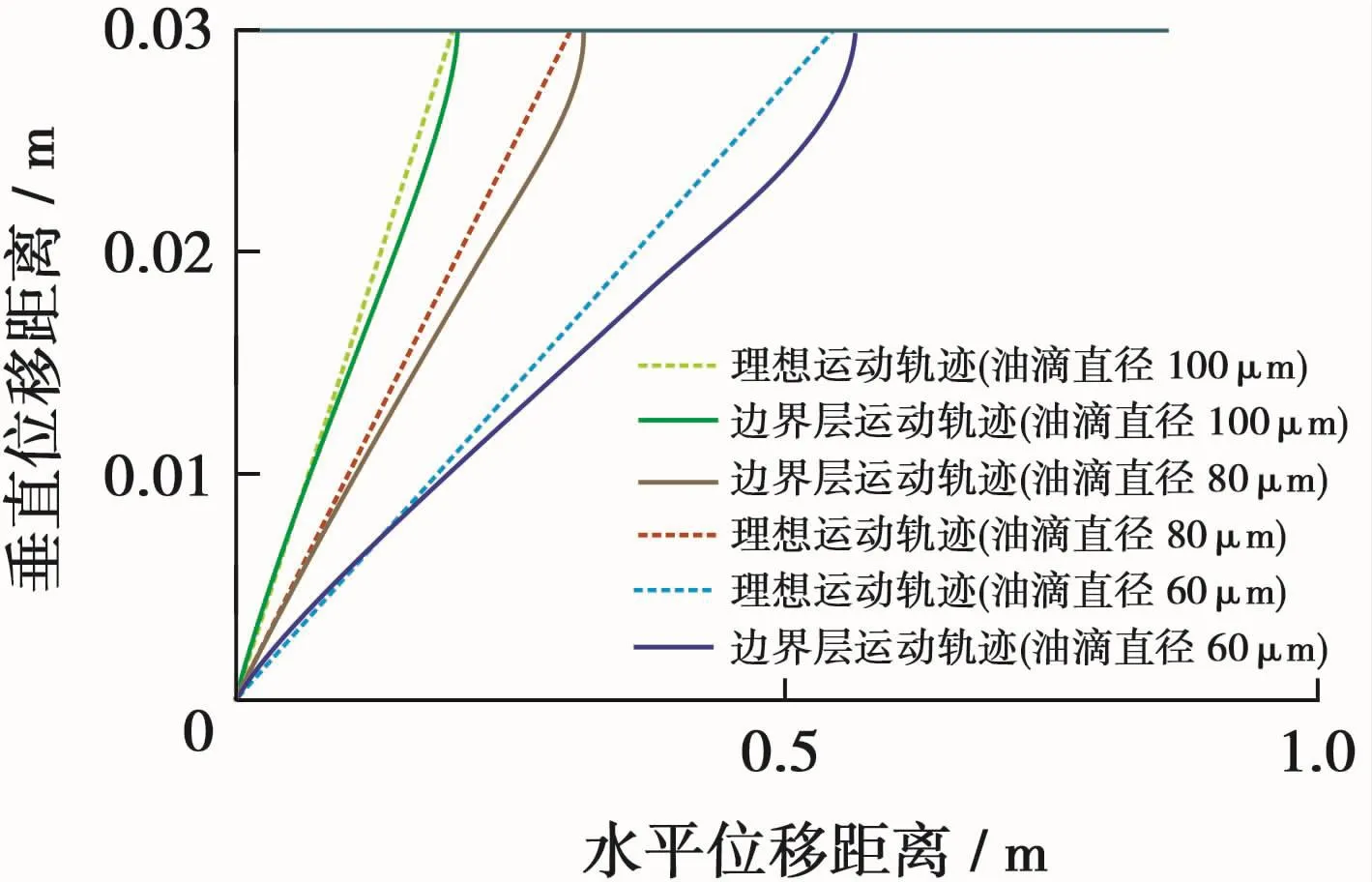
图8 进口段流动油滴位移轨迹（运动粘度为0.36×10－6m2／s）

当板间距由0.03 m增加到0.04 m时，直径60μm油滴在1 m距离内不能到达上板，直径100、80μm油滴水平位移距离分别比理想流动时增加2.6%和3.33%，比板间距为0.03 m时稍微有所减小，但水平位移距离绝对值增加25%（图9）。

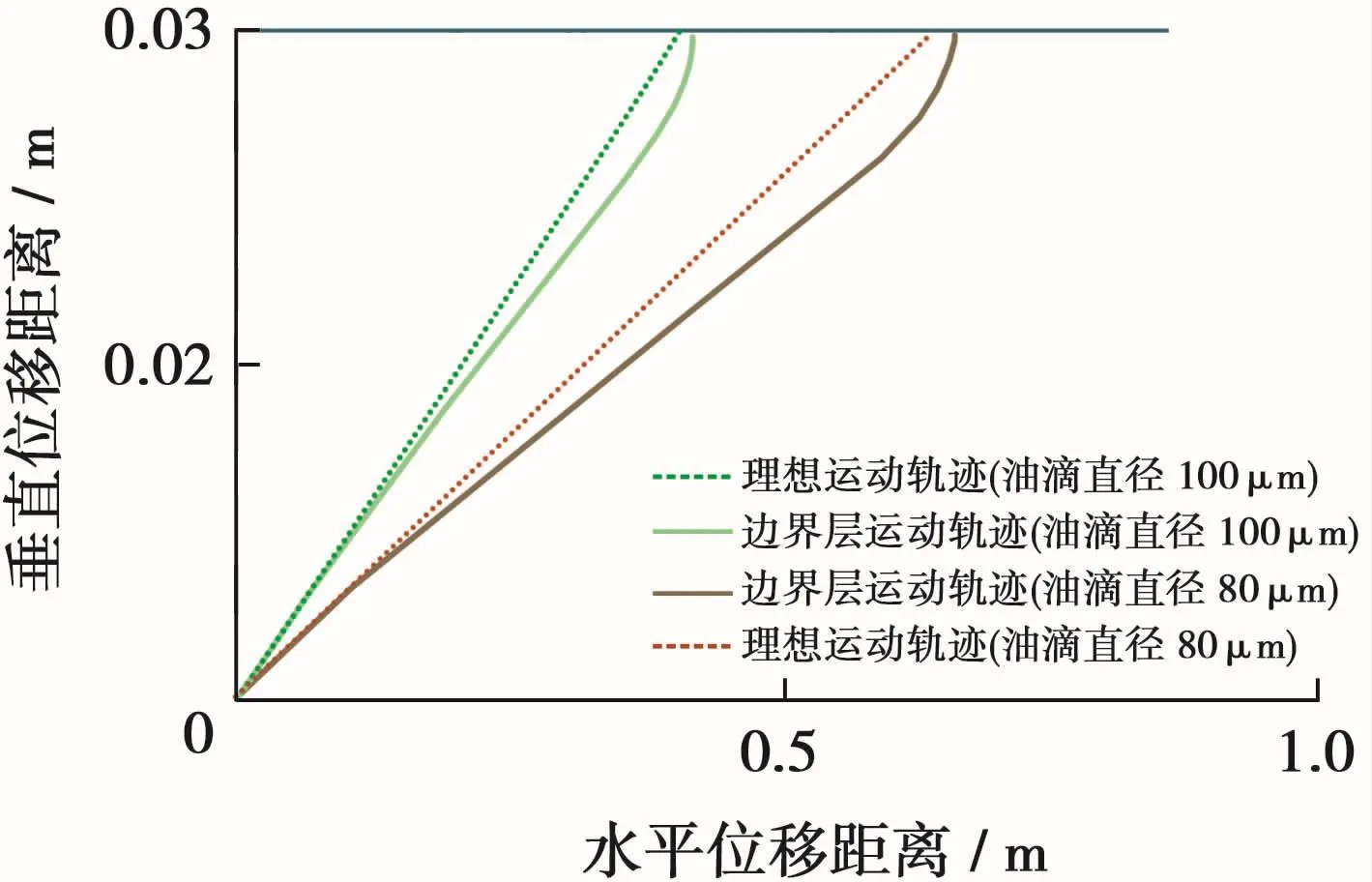
图9 平板间油滴位移轨迹（板间距离为0.04 m）

通过上述算例分析可知，在层流状态下，相同直径的油滴垂直位移到上板的时间都相同，不同的是水平位移距离和轨迹。分析认为，这种差异产生的主要原因为：

1）边界层与理想流场的差异。在靠近下板前缘附近，边界层厚度比上板靠后附近的边界层厚度要小很多，但水平方向速度却大很多。油滴在进口段运动时，水平方向位移差异随油滴直径减小而增大，造成的总体差异在3.5%以内，无论怎样给定初值，都不会对油滴到达上板的水平位移距离造成太大的影响。在泊肃叶流动中，流动是轴对称的，所以在平行板间油滴的位移轨迹也对称，与理想层流状态下油滴到达上板的水平位移距离相等。

2）边界层的几何形状与泊肃叶流动的几何形状不同。尽管在一个平板上的边界层厚度计算公式已经被实验证明，但其能否用于封闭的两个平板间的边界层厚度计算尚无定论。由于边界层厚度的连线是抛物线形式，且抛物线的开口朝向x轴远端（图3），而在边界层相交点的泊肃叶流动区域的抛物线开口朝向x轴前端（图1），这种几何形状上的不同可能会造成计算边界层内速度时存在一定差异。因此与实际斜板装置计算可脱除油滴直径相比，考虑边界层条件时油滴的实际运移距离比理想状态计算出的运移距离长5%～7%，对除油效果有一定影响，因此在斜板除油器设计中应充分考虑。

4 结论与建议

1）根据施利希廷平行管道边界层研究成果推导出了计算平板间边界层流体速度的公式，此公式符合粘性不可压缩流体运动的连续方程。即使势流核内断面速度由于边界层慢速的影响而存在不是常数的可能，只要差异不大，也可以近似地使用。

2）考虑边界层条件时流体速度分布规律与理想流体明显不同，靠近下板前缘附近的边界层厚度比上板后部的边界层厚度要小很多，但水平方向流体的速度却大很多。无论边界层厚度连线是什么形式，原点和上下边界层的交点的位置是相对固定的，这种流场速度分布的总趋势是一致的。建议在以后设计和研究中，应充分考虑边界层流场特征，扬长避短，利用后部“慢速”的水平流动特征，在保证层流条件下优化板组的结构。

［1］ 段明，王虎，张健，等．旅大10-1平台污水效果影响因素分析［J］．中国海上油气，2010，22（6）：420-423．

［2］ 戚俊清，刘亚莉，许培援，等．斜板沉降器板间距对处理负荷的影响［J］．郑州轻工业学院学报，1999，14（4）：51-55．

［3］ 李玉柱，贺五洲．工程流体力学：上册［M］．北京：清华大学出版社，2011．

［4］ 朱克勤，许春晓．粘性流体力学［M］．北京：高等教育出版社，2009．

［5］ 章榟雄，董曾南．粘性流体力学［M］．北京：清华大学出版社，2011．

［6］ 郭永怀．边界层理论讲义［M］．北京：中国科技大学出版社，2008．

［7］ HERNMANN S．Boundary-layer theory［M］．McGraw-Hill Book Company，1979：185-186．

Fluid velocity calculation in boundary layer and difference analysis between two parallel plates

Chang Qinglin
（Engineering Department of CNOOC，Beijing，100010）

A fluid velocity formula in boundary layer between two horizontal parallel plates is derived based on relative theory of viscous fluid mechanics and research of Schiliting H．about flow in a inlet length of a straight channel．On some given assumptions，we checked computations with the motion law of Stokes of oil droplets and analyzed the reason of the differences．The Calculations show that the flow is different between the cases of boundary layer and ideal laminar．The former horizontal movement distance of oil droplets is 5%～7%longer than those in ideal laminar conditions．It will decrease the oil removal efficiency and should be taken into consideration in the design of inclined plate separator．

parallel plates；fluid velocity of boundary layer；thickness of boundary layer；difference analysis

2013-04-24改回日期：2013-06-02

（编辑：叶秋敏）

常青林，男，高级工程师，1986年毕业于原武汉地质学院石油及地球物理勘探专业，现主要从事工程项目管理工作。地址：北京市东城区朝阳门北大街25号（邮编：100010）。电话：010-84521456。