深度图像的分层图割算法研究

俞江明，赵杰煜，汪国锋

1.宁波大学信息工程与技术学院，浙江宁波 315211

2.浙江省福利彩票发行中心，杭州 310000

深度图像的分层图割算法研究

俞江明，赵杰煜，汪国锋

1.宁波大学信息工程与技术学院，浙江宁波 315211

2.浙江省福利彩票发行中心，杭州 310000

1 引言

图像分割作为图像理解和识别的基础在计算机视觉中有重要的作用，但由于图像的复杂性，没有很好的通用的图像分割算法能解决所有的问题，即便如此还是有前赴后继的国内外学者投入到图像分割的研究队伍当中。在近几十年的研究当中，图像分割已经取得了非常大的进展。

在以往的图像分割算法中，有基于区域颜色信息的分割[1-2]，也有基于边缘信息的分割[3-4]，但由于利用的信息太少，都不太能达到理想的分割效果。

基于图割的算法由于其非常巧妙地结合了区域颜色和边缘信息而在最近成为了研究的热点，图割算法应用于图像是有Greig等[5]人在1989年完成，后续的研究也有如文[6]应用于二值图像，但其在很长时间没有得到重视，直到本世纪初Boykov等人[7]明确了图割算法应用于图像上图的定义以及权值的确定，并且在基于增广路算法的最大流算法基础上提出了更为高效的求解最大流的算法[8]，他们开创性的工作引发了再一次的图割热，基于图割的算法层出不穷[9-10]。

Rother等人在文献[11]中用迭代图割算法来减少用户交互，只需三四次迭代即能得到精确的分割结果。由于其非常耗时的缺点，后续的以迭代图割为基础的研究通常是在不降低分割精度的前提下来提升分割的速度，取得了比较好的效果，如文献[12-13]把分水岭算法过分割的缺点和图割算法耗时的缺点结合，用分水岭算法的结果作为图割算法的超像素，很好地弥补了两种方法各自的不足。文献[14-15]结合多尺度的金字塔结构来减少图割算法的混合高斯EM算法的数据规模，采用三到四层塔结构，正好接近于Rother等[11]人的迭代算法步骤数，在减少初始化时间的情况下，没有降低最后的分割精度。但其采用最高像素值来抽取金字塔上层的像素不利于噪声的去除。图割算法应用于图像的另一个分支这是加入形状先验，分割边界除了要是梯度最大化之外还要符合形状先验的约束，如文献[16-17]中的Kolmogorov等人，但是由于其能量函数不再符合文献[18]的能求得全局最优解的要求，只能通过近似方法来求得图像分割的边界，往往非常耗时。

本文在前人[14-15]的基础上采用分层的金字塔模型，在提取上层像素中采用下层对应的像素的中值，能有效地解决噪声问题。深度信息的利用也不像Boykov等人[7]那样采用直接合并的方法，而是引入平衡因子来决定想要利用的深度信息相对于颜色信息的重要程度，深度信息的建模采用直方图建模，引入直方图的目的是为了计算平衡因子的方便，而且深度信息是一维信息，直方图建模是非常快速的。本文的基于深度图像的分层迭代图割方法取得的结果优于迭代图割算法而所需的时间却大大缩短。

2 图割理论基础与改进

2.1 能量函数

图割理论应用于图像处理，要求是交互式的图像分割，交互式图像分割给了用户希望划分的目标的先验信息，这些先验信息往往可以增加图像分割的准确度，减少分割难度。用户给定一些像素作为希望分割的目标，一些像素作为图像的背景，把这些信息当做图像分割的先验信息，即硬约束。其余部分的像素就自动分割出来，只需求得符合这些硬约束的图像分割中最优的那个分割即可。

首先定义分割为一个图像的分割边界，要求得到图像的最优割，需要定义惩罚函数，惩罚函数也可称作能量函数，最优割对应着能量函数最小值。能量函数可以分为两个部分，一个代表割的边界信息，叫做边界项，另一个代表割的区域信息，叫做区域项，这两项同时对应着图像的软约束和硬约束。硬约束就是用户已经给定的先验知识，软约束是保证同一前景或同一背景的相邻像素间的平滑性而引入的。

假设一幅图像用数学表示为：oi(i=1,2,…,N)，其中oi表中图像中的第i个像素，像素按图像的行排列，N表示图像中像素的个数。用li表示第i个像素所对应的标签，li取值范围为li∈{0,1}，通过MAP-MRF可以得到图能量函数的表达式如下：

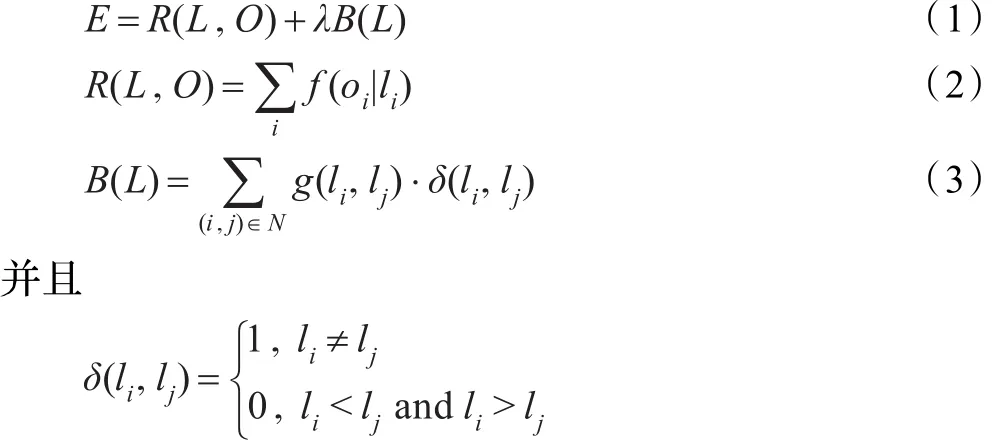
式（1）中能量函数E中的R(L,O)即对应了割的区域信息，而B(L)则代表了一个割的边界信息，λ≥0为区域似然项R(L,O)相对于边界梯度项B(L)的相对重要程度。区域项R(L,O)表示了把一个像素赋给前景或背景的惩罚。在实际的操作中，往往首先用用户给定的硬约束，即哪些像素属于背景，哪些像素属于前景，根据这些像素分别建立前景和背景的概率模型，而R(L,O)就表示观察的像素值oi与前景或背景概率模型的符合程度，如果观察值oi与前景概率模型很相似却给了背景的标签则惩罚值会很大，反之则会很小。平滑项B(L)表示了一个图像分割L的边界性质。g(li,lj)表示了对相邻像素oi，oj之间的不平滑的惩罚，惩罚项可以采用很多形式，比如梯度，或者是方向梯度等等[7]。

区域似然项R(L,O)是图像中的观察像素值与前景和背景概率模型的相似程度，在公式（2）中通过f(oi|li)可以得知给标签li值0则表示观察值和背景概率模型是符合的，如果给标签li值1则表示观察值与前景概率模型是符合的。

在Boykov等人[7]的图割算法中利用直方图作为概率模型，并且认为他们的方法可以推广到N维图像，但是事实上直方图在对高于二维的数据进行建模时将变得非常困难，在文献[11]中已经提到，他们在彩色图像中采用的是混合高斯模型，并且减少了用户的交互。本文由于引入了深度信息概率模型的选择将对分割的有效性产生重大影响，考虑到深度信息是一维的可以采用快速的直方图建模，颜色文理信息仍然采用混合高斯模型，两者之间的权衡用平衡因子α来表示。假设用P(oi|F)表示前景概率模型，P(oi|B)表示背景概率模型，则根据上面描述可以定义加入深度信息的概率模型如下：

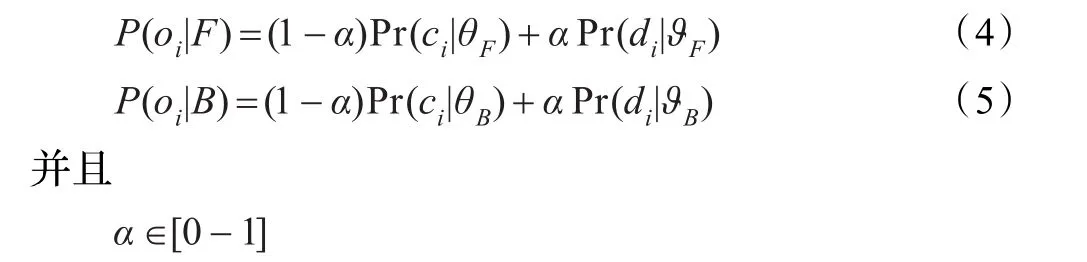
其中ci表示图像像素的RGB观察值，di为从图像的深度信息，θF为前景混合高斯模型的参数，θB为背景混合高斯模型的参数，ϑF为前景直方图概率模型的参数，ϑB为背景直方图概率模型的参数。其中Pr(ci|θF)和Pr(oi|θB)表示的前背景混合高斯概率模型的具体公式如下：

其中zi为维度为C的单位向量，假设图像深度信息的最大值为D，则zi中第[di·C/D]为1，表示di属于直方图中的哪一个类别，表示用户标定的数据统计的直方图类别概率，nk表示第k类的样本个数，E为样本总数。这样基于深度的直方图概率模型通过样本概率的形式可以简单地用数学公式表示出来。以上就是全部的概率模型公式，其中的颜色部分利用了和文献[11]中类似的混合高斯模型，事实上他们已经通过实践确定用直方图来建立高维的概率模型是很难实际操作的，对于深度的建模，采用的是直方图建模，因为混合高斯求解的时候要用到EM算法，而EM算法是循环迭代的算法，其时间复杂度较高，但是直方图却能在很短时间内建立一维数据的概率模型，对于深度信息的建模是非常合适的，并且在本文的方法中对于深度的直方图建模的α的确定也是有利的，本文的α就是在直方图概率向量的基础上来确定的。总之，选择直方图来概率建模不仅耗时较少，而且有利于本文的深度信息与颜色信息之间重要性的平衡。

2.2 权值确定和图结构

在图割算法中，一般把图中的每个像素看成数据结构中图的节点，通过前面的马尔科夫随机场的马尔科夫性质假设每个像素的标号只受相邻像素的标号的影响，本文采用的是8邻域系统，所以像素之间的边的连接如图1所示。

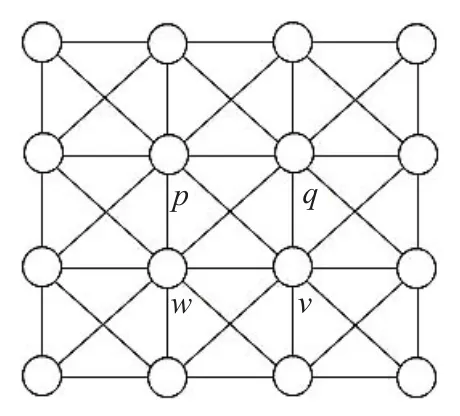
图1 邻域系统

在图1的基础上加入两个额外的节点一个是source节点一个是terminal节点，简称S节点和T节点，S代表目标，T代表背景，并把图中所有的像素节点与这两个节点相连接。

在图割算法的图模型中，图中的节点包括每个像素对应一个节点外加两个终结节点，一个是S节点，一个是T节点，S节点又叫目标节点，找到最小割以后与S仍然相连的节点即为所要提取的目标物体，相应的T节点又叫背景节点，执行最大流算法找到最小割以后与T仍然相连的就是背景。

图中的边如前所述，也可以分为两类边，一类是n-link，为图中相邻像素节点之间的连接边，一类是t-link，为像素节点与终结节点之间相连边，图2表述了以上的节点和边。

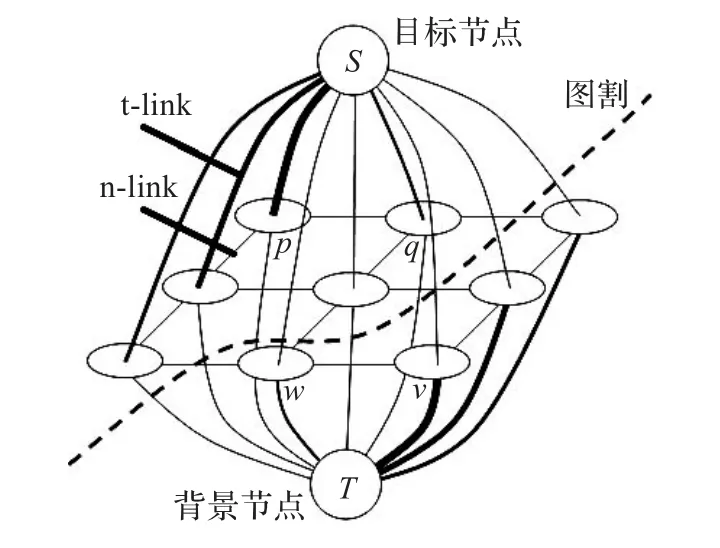
图2 图割算法图结构

如图所示的两类边如果细分可以分为三类，一类是与S相连的t-link，一类是与T相连的t-link，这两类边的赋值与2.1小节的概率模型相关，采用与文献[5]类似的log-likelihook函数，n-link采用ad-hoc函数，其中深度信息在ad-hoc中的引入也采用概率模型类似的方法，引入平衡因子α，来平衡深度信息在惩罚项中的重要性。剩下的问题将是如何确定α，由于引入了直方图来对深度信息建模，看到由直方图组成的概率向量能清楚地表达深度信息的分布，而这种分布之间的差异可以用向量之间的距离来表达。

图3即为一个关于深度信息的概率直方图，前景和背景的概率直方图类似。给出的是前景深度的概率直方图。

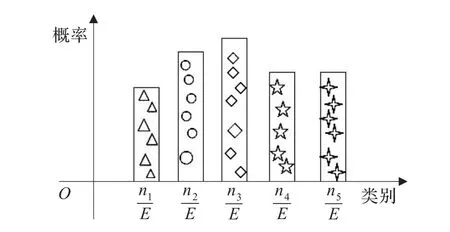
图3 深度信息直方图

不同的图形即表示不同的类，柱状的高低则表示概率大小，这样由概率组成的向量可以完全表示直方图的形状，向量之间的距离可以表示直方图之间的差异程度，而且在概率直方图中可以直接来用于α值，即：，由如上公式可知0≤α≤1，并且α值越大则说明前背景之间的深度信息差异越大，仅仅依靠深度信息即能有效地把目标分割出来。

对于图割来说权值确定是非常重要的，怎样有效地利用不同的信息以及这些信息之间有效地结合在一起从而达到对图像的有效分割，各种颜色、文理、深度以及区域边界之间的结合和平衡的掌握对于一个图像分割的方法来说非常重要。如前所述，已经对于两种t-link和一种n-link的值的确定已经基本了解，t-link采用log-likelihoods函数，n-link采用ad-hoc函数，但是与S节点相连的t-link和与T节点相连的t-link都是采用log-likelihoods函数，它们的概率模型训练的参数却不一样，即虽然它们有相同的概率模型，都是混合高斯模型和直方图模型结合的概率模型，但是人为先验却是不同的，用户交互时已经把需要的前景像素和背景像素基本确定，所以以两种不同的权值来定义这两类t-link，具体的权值如表1所示。

表1 各种边的权值

通过α可以有效地结合颜色纹理和深度信息，使图像在前背景颜色相似却深度不同的情况下能有效地利用深度的不同，即α值的偏大而偏重利用深度信息，这对于自动的图像分割是非常有效的，能自动确定图像分割时所利用的深度信息和颜色信息的比重，从而得到精确分割。

2.3 分层求解

通过实验发现图割算法求解是非常缓慢的，而图割中时间的消耗主要在于混合高斯概率模型的EM迭代算法，这种循环迭代的耗时是非常不可容忍的，因为在迭代图割算法中前几轮迭代中用户给出的前景信息大概只是包括了前景信息，同时也包含了背景的信息，同时前几轮的分割也没有达到精确的分割，分割的目的是在最后一步分割中得到理想的分割要求，了解到这样后，由于通过大量实验绝大部分情况下，图割算法只需迭代三到四轮后就可以得到用户理想的要求，很多国内学者了解到此种情况后，纷纷用多尺度的方法来加快EM概率建模的过程，把图像金字塔建立三四层高度使得和迭代图割算法的迭代次数相当的情况下，可以有效地减少得到理想图割效果的时间，并且不降低分割的精度，这是肯定的，因为既然图割算法的大部分时间花在概率建模上，在初始的阶段又不需要精确的概率模型。通过多尺度来降低建模的样本数量当然可以有效地减少分割所消耗的时间。

如文献[14-15]就是通过多尺度来研究迭代图割加快算法的一个例子，他们通过取四邻域中的最大值作为图像金字塔上层的像素来对上层进行概率建模，这种取最大值的方法对于图像有噪声的情况下是非常不利的，他们的分割加快算法明显忽视了图像噪声的情况，并且对于没有噪声的情况下，去最大值也是很牵强的。本文采用了多尺度的思想，但是幅度更大，不是通过四邻域来对图像像素进行抽取，而是通过四领域，这种大幅度的抽取过程可以通过桶排序来有效地抽取典型样本，从而有效地避免噪声点和不重要的样本点，另一层原因是在深度信息往往含有很多噪声点，这些点的深度信息由于透明或者别的什么原因而无法获取，如果利用去掉最大和最小的颜色和深度都典型的样本点，然后用样本点的深度信息，来对那些无法获取深度信息的噪声点的信息进行替换，则可以取得一举两得的好处。通过对小样本的一遍扫描即可排除那些噪声点也不会对分割时间产生很大的影响，消耗时间和文献[14]是一样的。文献[16-17]中的分水岭算法在分水岭的过分割的基础上，把分水岭的分割结果当做图割算法的超像素，虽然也能做图像分割，但是分水岭方法无法适用于深度图像。

本文采用2×2小块作为上层图像像素的抽取单位，通过找出2×2像素中颜色绝对值和最大和最小的像素点，并且找到深度信息最大和最小的像素点，排除这些像素点后，如果剩余的点还有，则用剩余的点代表这4个点，如果没有剩余的点，则忽略深度信息的最大和最小点，用颜色信息所剩余的两个点作为抽样点来进行上层图像的搭建，通过此方法得到的样本像素点可以充分代表图像的本质信息而不会受噪声点以及深度信息无法获取的点的影响。

2.4 能量最小化

对于图割算法来说，最重要的就是图结构以及图中边权值的确定，求解可以采用最大流/最小割算法。文献[8]对于图割算法求解的最大流/最小割算法进行了实验性的研究，发明了一种虽然在理论上时间复杂度比一般最大流算法的时间复杂度O(ne2)高的算法，它的理论最大复杂度为O(|c|ne2)，其中|c|为割的数量，但在实际的实验过程中由于图割算法图的特殊性，导致这个算法可以比一般的算法节省几倍的时间，它是通过在图的两端构建树并扩展和领养孤儿节点来增加图中的通路，并最终求得最大流。本文采用了文献[8]类似的方法来求解最大流。

3 改进图割实施流程

本文的方法是融合深度的分层图割算法研究，此算法的精髓在于用直方图来对深度信息建模，并且引入平衡因子α来对图像的颜色纹理信息和深度信息之间的协调因子，当前景和背景的深度信息相差明显时，α因子就接近于1，也就是说仅仅依靠深度信息就能够很好地分割出图像中的目标，当前景和背景的深度信息相差不大时，α接近于0时，就利用颜色和纹理信息来对图像进行分割。除了引入深度信息，对于分层的引入也能够加快图割算法的步骤，因为如文献[11]中所述图割只有在最后一次循环时才得到精确的分割结果，所以前几次的前景和背景的分层提取并不影响最终的分割结构。

下面详细阐述算法的总体流程，首先的第一步是用户用鼠标拖出一个矩形框，在矩形框中的像素为可能前景，但是在概率建模的时候先当这个矩形框内的为前景，至少它包含了前景的像素，在循环迭代的过程中，一次一次地以上一次的分割结果作为下一次的概率建模依据就能逐渐接近于用户想要的概率模型。在矩形框外的就是绝对背景用它作为背景概率建模的样本数据。以用户的矩形和图像作为本算法的输入，接下去就是执行本算法，算法的第一个基本初始化工作时建立三层金字塔，以2×2为提取像素的基本单位，在源图像的基础上以2×2为单位提取这当中的样本像素，扫描这4个像素找出其中的颜色绝对值最大的和最小的像素，并且同时扫描深度图像也找出深度的最大值和最小值，在去除这四个像素的基础上，用随机算法在剩下的像素中随机选择一个像素用作多尺度图像分割上层的概率建模样本，同理可以在提取一次建立三层的图像金字塔。当这些初始化工作做好之后，在最上层用EM算法对颜色进行混合高斯建模，并通过一遍扫描深度图建立深度信息直方图，即概率向量，再同时结合用户给定的矩形框，当然在金字塔上层时矩形框也要相应的缩小，建立前景概率模型和背景概率模型，用得到的概率模型结合表1建立起图割算法的图结构，建立图结构时是用原始图像来建立的，也就是说执行最大流算法时在原图上进行，在第二次迭代中通过第一次得到的分割结果，再通过2×2的样本抽取方法，在图像金字塔的中间层建立起概率模型，再在原始图像上通过重新建立起来的图结果执行最大流算法得到分割结果，最后就一直在原始的图像上建立概率模型和执行最大流算法分割。虽然只进行了3层的多尺度的结合，但是对于迭代图割算法的结合是非常到位的，因为通过大量实验得到在大部分的情况下，图割的执行基本上3～4次就能得到理想的分割效果，下面以更加简洁的语言及步骤来解释本文算法的流程：

（1）对于图像像素，用户通过框定矩形得到图像的可能前景和绝对背景。

（2）通过2×2的样本抽样建立起三层的图像金子塔，抽取方法如上所述，去掉极端值随机选择算法。

（3）在最上层图像上进行EM混合高斯和直方图概率建模得到前景和背景的概率模型，概率模型公式如下：

（4）建立图割图结构执行最大流改进算法。

（5）执行边界映射到第二层继续概率建模。

（6）建立图割图结构执行最大流改进算法。

（7）分割结构在原图上建立概率模型。

（8）执行步骤（6）直到分割满意为止。

以上就是本文提到的深度图像分层分割的全部算法流程，其优点在于利用直方图来对深度信息建模，并通过引入平衡因子α来对颜色纹理信息和深度信息之间进行自动的取舍，并用分层提取的方法避免噪声和有效地加快图割算法的执行时间。在前人研究的基础上可以说做了很大的改进，改进的方式在于引入了深度信息，可以利用更多的信息来进行图像分割后，怎样平衡这引入的信息和原来信息之间的重要性程度将是非常关键的，在以往的前人的研究中都只是单纯当做新的一维的信息而加入到混合高斯模型中去建立四维的混合高斯模型，这种不加区分的加入虽然也能取得一定的效果，通过引入平衡因子则更加有效。下面将给出本文方法的实验结果和对实验结果的分析。

4 实验结果与分析

利用本文算法来对图像进行分割，在时间和分割进度上来对标准的图割算法进行对比，在分割精度基本不变的情况下大大缩短了分割所需的时间，并且可以在颜色信息无法正确区分的情况下依然对图像进行正确的分割。

由于本算法实行的是深度图像的分割，而一些图割算法的标准图没有深度信息，所以本文采用随机生成灰度图的方法来自动生成深度信息来对标准图形进行分割，由于是随机生成的，所以前景和背景的深度信息直方图即概率向量基本相同，这导致平衡参数α非常小，所以本质上来说主要看的还是颜色纹理信息，并不影响分割精度，接下去就把这种用自动生成的深度图的方法应用于图割算法的标准图中来对耗时和分割结果进行对比，目标是在耗时下降的情况下，分割的精度上却没有下降。

有图可知，在图4（a）的原始图像输入和用户矩形输入的情况下，本文的算法可以建立起图像金字塔模型，每层图像都是前一次的分割结果的输入，第一次的输入是用户输入的矩形，由图4（b）可知图像的概率模型是在图像金字塔基础之上的，每次的分割结果都用黑线来表示，在黑线内部为用作前景概率建模的像素样本，在黑线以外的是用作背景概率建模的像素样本，由于深度信息采用的是随机生成的灰度图，实验得到的三次结果的α都很小，每一次α≤0.01基本不起什么作用，所以可以看出基本还是颜色的混合高斯模型在起作用，但是时间却大大缩短，下面给出三次迭代的时间消耗比。

图4 算法精度对比

由图5和表2可知算法在前面阶段上的耗时减少了将近一半，在总体上的算法执行时间也节约了30%，但是图像分割最后的精度却没有受到任何影响。

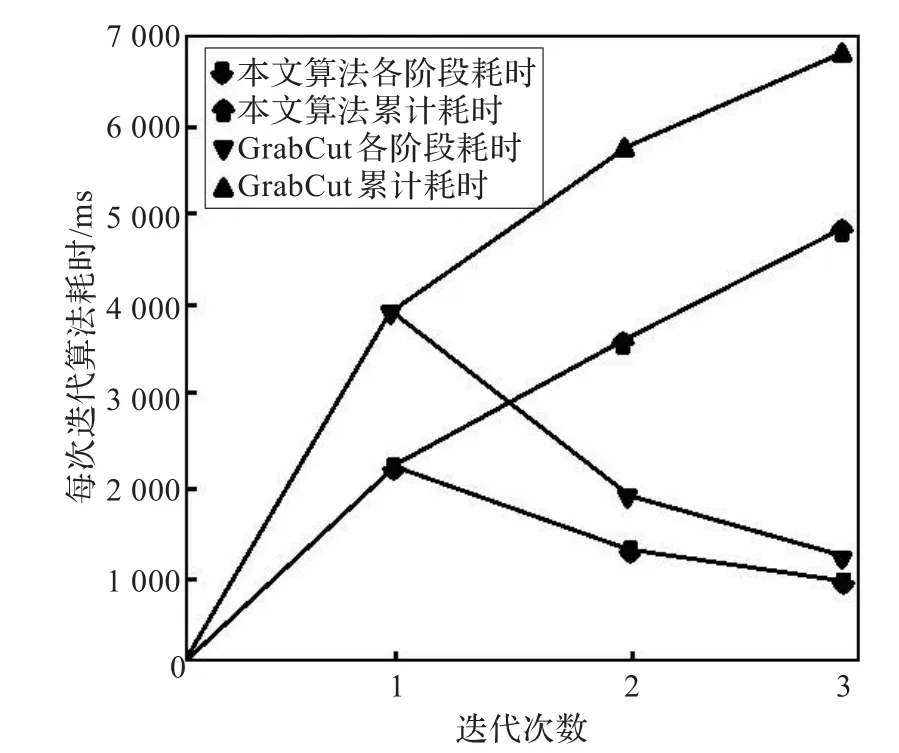
图5 算法时间对比

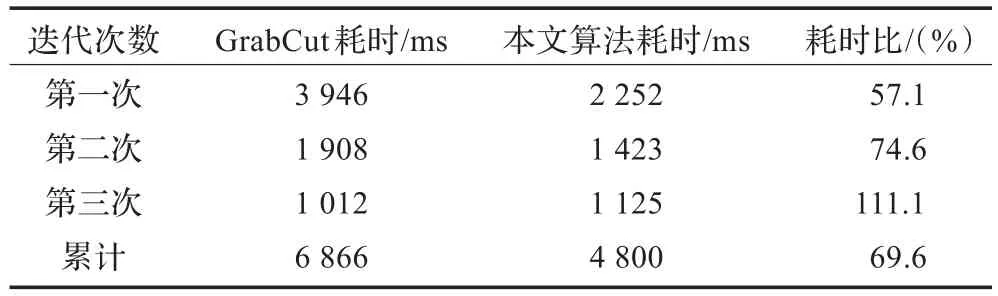
表2 算法耗时比

下面再用真正的深度图像来作为算法输入，比较两算法的性能。

图6 （a）RGB图像

图6 （b）深度图像

图7 深度图像分割结果比较

图7左边为迭代图割算法的分割结果（深度信息单纯作为第四维信息）右边为算法分割结果由实验结果发现此时的深度信息在实验过程中将起决定性作用，事实也是这样通过追踪α的值可知，在三次迭代中α的值都大于0.7由此可知完全可有深度信息作为图像分割的依据，由图7可知单纯把深度作为第四维信息加入到混合高斯建模中是行不通的，这样完全不知道深度信息的重要性。通过实验得知算法可以自动判断深度信息的重要程度，从而来对深度图像进行正确分割，在深度信息明显时利用深度信息，在深度信息不明显时则利用颜色信息来对图像进行分割。

5 结论

虽然本文改进了迭代图割算法的执行效率，对深度图像的深度信息进行了有效的利用，但是本文的方法也有很大的局限性，且并没有确切给出σ的计算公式，在迭代图割算法中利用了矩阵来求σ的值，本文也只是在其中加入深度信息，单纯地利用四维矩阵求出了σ的值，在以后的研究中，将对这里做改进，以期能更好地理解图割算法的意义和图割算法的性能。

[1]Reese L J.Intelligent paint：Region-based interactive image segmentation[D].Brigham Young University，1999.

[2]Najman L，Couprie M，Bertrand G.Watersheds，mosaics，and the emergence paradigm[J].Discrete Applied Mathematics，2005，147（2/3）：301-324.

[3]Mortensen E N，Barrett W A.Interactive segmentation with intelligent scissors[J].Graphical Models and Image Processing，1998，60：349-384.

[4]Lindeberg T，Li M X.Segmentation and classification of edges using minimum description length approximation andcomplementaryjunctioncues[J].ComputerVision and Image Understanding，1997，67（1）：88-98.

[5]Greig M D，Porteous B T，Seheult H A.Exact maximum a posteriori estimationfor binaryimages[J].Journal of the Royal Statistical Society，1989，51（2）：271-279.

[6]Shi J，Malik J.Normalized cuts and image segmentation[C]// CVPR，1997：731-737.

[7]Boykov Y，Jolly M.Interactive graph cuts for optimal boundary ®ion segmentation of objects in N-D images[C]//ICCV，2001.

[8]Boykov Y，Kolmogorov V.An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision[C]//EMMCVPR，2001.

[9]Delong A，Veksler O，Boykov Y.Recursive MDL via graph cuts：Application to segmentation[C]//ICCV，2011：890-897.

[10]Jegelka S，Bilmes J.Submodularity beyound submodular energies：Coupling edges in graph[C]//CVPR，2011：1897-1904.

[11]Rother C，Kolmogorov V，Black A.GrabCut：Interactive foreground extraction using iterated graph cuts[J].ACM Trans on Graphics，2004，23（3）：309-314.

[12]刘荣，彭艳敏.基于分水岭与图割的自动分割方法[J].北京航空航天大学学报，2012，38（5）.

[13]Couprie C，Grady L，Najman L，et al.Power watershed：a new image segmentation framework extending graph cuts，random walker and optimal spanning forest[C]//ICCV，2009.

[14]徐秋平，郭敏，王亚荣.基于多尺度分析与图割的快速图像分割算法[J].计算机应用研究，2009，26（10）.

[15]Li Y，SunJ，TangCK，etal.A multilevelbanded graphcutsmethodforfastimagesegmentation[C]// Proc of ICCV，2005：259-265.

[16]Vicente S，Kolmogorov V，Rother C.Graph cut based image segmentation with conectivity priors[C]//CVPR，2008.

[17]Vicente S，Kolmogorov V，Rother C.Joint optimization of segmentation and appearance models[C]//ICCV，2009.

[18]Rother C，Kolmogorov V，Boykov Y，et al.Interactive Foreground Extraction using graph cut[R].Microsoft Technical Report，2011.

YU Jiangming,ZHAO Jieyu,WANG Guofeng

1.Research Institute of Information Science and Technology,Ningbo University,Ningbo,Zhejiang 315211,China
2.Zhejiang Provincial Welfare Lottery Center,Hangzhou 310000,China

Based on the iterative graph cut method,this paper uses image pyramid to accelerate the speed of segmentation and introduces a balance factor to determine the significance between the color and depth information.This method can segment the depth image easily and precisely with the pyramid and the balance factor.The balance factor is the measure of the discrimination for the color and depth information.If the depth information is sufficient to distinguish the object from the background,then the depth information plays a more important role in the segmentation process,otherwise the color information takes more important role.By using the image pyramid our method can interact with the iterative graph cuts and greatly reduces the processing time without influencing the segmentation precision.

iterative graph cuts;balance factor;Gaussian mixture;depth histogram

以深度图像为分割对象，在迭代图割算法的基础上，通过引入分层机制加快图割执行速度，并通过引入平衡因子来平衡颜色纹理和深度之间的重要程度，从而有效地对深度图像进行分割。利用平衡因子可以在深度信息能够明显区分前背景的情况下，重点利用深度信息来分割图像，反之则重点利用颜色和纹理信息。而在迭代图割算法中，分层机制的引入能够在不降低分割精度的情况下有效地减少图割算法的执行时间。

迭代图割；平衡因子；混合高斯；深度直方图

A

TP393

10.3778/j.issn.1002-8331.1212-0363

YU Jiangming,ZHAO Jieyu,WANG Guofeng.Depth image segmentation using layered graph cuts.Computer Engineering and Applications,2014,50（22）：183-188.

国家自然科学基金（No.61175026）；浙江省自然科学基金重大项目（No.D1080807）；国家国际科技合作项目（No.S2013GR0113）。

俞江明（1987—），男，硕士研究生，主要研究领域为图形图像处理，模式识别；赵杰煜（1965—），男，博士，教授，主要研究领域为图形图像处理；汪国锋（1971—），男，工程师，主要研究领域为计算机网络和数据库。E-mail：yjm_luohua@sina.com

2012-12-30

2013-03-04

1002-8331（2014）22-0183-06

CNKI网络优先出版：2013-03-29,http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1540.002.html