基于扰动免疫粒子群和K均值的混合聚类算法

许竣玮，徐蔚鸿

长沙理工大学计算机与通信工程学院，长沙 410114

基于扰动免疫粒子群和K均值的混合聚类算法

许竣玮，徐蔚鸿

长沙理工大学计算机与通信工程学院，长沙 410114

1 引言

聚类是信息处理和数据挖掘领域的重要技术之一，人们对它的关注度已经越来越高。K均值聚类算法在数据识别方面有着重要的作用，该方法是选取距离来作为相似性度量，然后确定评价聚类结果质量的准则函数，最后采用迭代的方法找出使准则函数达到极值的最优聚类结果。该方法由于简单、高效而且需要设置和调整的参数少等优点被应用到了很多领域。但是该方法存在对初始化的依赖性较高、在多峰函数中容易过早收敛等问题，因此，算法有时候会出现陷入局部最优解的现象。

为解决这类问题，学者们对这一领域做了大量的研究，文献[1-3]将遗传算法等优化技术用来解决陷入局部极值的问题，但是实验表明，当聚类规模较大时，这些算法容易出现早熟收敛的现象。和遗传算法相比，粒子群算法（PSO）具有较强的全局搜索能力，通过调整参数，PSO的局部搜索能力也可以得到提高，适合编程处理。文献[4]提出的免疫接种粒子群的聚类算法在粒子的迭代过程中加入了免疫算子，但是该算法中的疫苗是全局最优解，因此疫苗的多样性不高，从而影响了整个种群的多样性。文献[5]提出的改进的粒子群和K均值混合算法中的随机变异操作导致粒子变异不具备优化特性，而且单个粒子变异搜索的空间非常有限，找到全局最优解的概率较小。文献[6]提出的基于粒子群的聚类算法采用基于K-中心点算法的改进策略，减少了迭代时间。但是该算法没有从根本上解决容易陷入局部最优解的问题。文献[7]提出的基于粒计算的K-medoids聚类算法对算法的初始化方式进行了改进，克服了传统K均值算法初始化的随机性和快速K-均值算法初始中心可能出现在同一类簇的缺陷，提高了聚类的收敛效率，但该算法中粒子的多样性较差，算法容易陷入局部最优解。文献[8]提出的一种新的粒子群优化聚类方法通过引入改进的交叉、变异算子在一定程度上提高了粒子的多样性。但算法通过变异跳出局部最优的能力较弱，且收敛精度不高。文献[9]提出的基于人工鱼群的优化K-means聚类算法提高了K均值聚类算法的初始化质量，算法中的“鱼”会逐渐向食物增多的方向移动，在处理较规则数据时，算法的聚类效果较好。但算法在处理不规则数据时，尤其对于在某个较大空间中有较大“食物浓度”的数据时，算法的聚群行为容易使其陷入该空间中，从而找不到最高的“食物浓度”，而且算法的聚群行为导致算法跳出局部最优解的能力较弱。文献[10]提出的一种有效的K-means聚类中心初始化方法在一定程度上提高了算法初始化质量，但是算法中的密度参数MinPts不易确定，过大会导致那些距离较远、密度较稀疏的粒子不能单独成为一类，从而导致聚类效果不佳，过小会导致算法的粒子中心点过多而失去算法原有的优势，不能达到预期的聚类效果。文献[11]提出的融合K-调和均值的混沌粒子群聚类算法利用变尺度混沌搜索提高了算法收敛效率、粒子的多样性和跳出局部极值的能力，但该方法仅对陷入局部极值的单个粒子进行了混沌变异，粒子搜索空间非常有限，因此，找到全局最优解的概率相对较小。

针对上述算法的优缺点，本文提出一种基于扰动免疫粒子群和K均值的混合聚类算法。该算法采用K均值将粒子聚类，选定具有最高平均适应度值的聚类域用于提取疫苗，因此，从该疫苗集中随机生成的免疫疫苗具有较强的多样性和较高的适应度值；当个体极值和全局极值的连续停滞更新代数超过所设置的阀值时，算法将扰动算子引入到粒子更新公式中，从而改变粒子群的运动方向，该运动具有很好的遍历性，因此该算法跳出局部极值的能力大大增强。最后，当粒子的扰动次数达到设置的阀值时，采用K均值算法进一步提高收敛精度。

2 粒子群优化算法

2.1 基本粒子群优化算法

1995年，PSO算法由美国的Kennedy博士和Eberhart博士提出[12]，它起源于对鸟群觅食行为的仿真。该算法简洁、易于实现，需要调整的参数不多，因此PSO算法引起了广泛的关注，并应用于目标优化、机器学习、数据挖掘、模式识别等领域。

PSO算法首先是随机生成一组初始化值，然后通过迭代搜寻最优值。在迭代过程中每个解都是解空间的一个粒子，粒子的搜寻速度决定了他们的飞行方向和飞行距离。最后，粒子们根据他们当前的飞行方向和飞行距离追随当前最优粒子在解空间中进行搜索，通过跟踪局部极值和全局极值及时更新自己，再通过自适应度函数判断新位置的自适应值，若不满足结束条件，则继续进行迭代，直到找到最优解。

粒子速度更新公式：

2.2 带扰动算子的粒子群优化算法

当PSO算法处于进化停滞时，粒子群中的粒子会出现聚集现象，文献[13]通过严格的数学推导得到式（3）：

由式（4）可知，粒子将聚集到由自身极值pu和全局极值pg决定的极值p*上，如果粒子在向p*靠近过程中没有找到比pg更优的位置，则进化将处于停滞状态，粒子会逐渐聚集到p*周围。因此PSO算法可以通过两种途径摆脱局部极值：（1）在飞向p*过程中发现比pg更优的位置，但是这个过程发现更优位置的概率较小，因为PSO已经陷入局部极值，pg周围已经过高密度的搜索。（2）调整个体极值和全局极值，使所有的粒子飞向新的位置p*'，经历新的搜索路径和领域，这样发现更优解的概率较大。本文采用第二种方法，将连续停滞代数t作为触发条件对个体极值和全局极值进行扰动，扰动算子为：

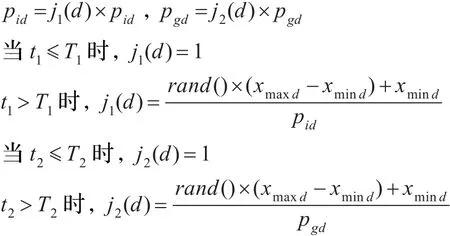
式中，t1是个体极值的连续停滞代数，t2是全局极值的连续停滞代数，T1是个体极值扰动所需的连续停滞代数，T2是全局极值扰动所需的连续停滞代数，j1、j2是K×D维向量，j1(d)表示向量j1的第d维分量，j2(d)表示向量j2的第d维分量。

引入扰动算子后的粒子i速度更新公式为：

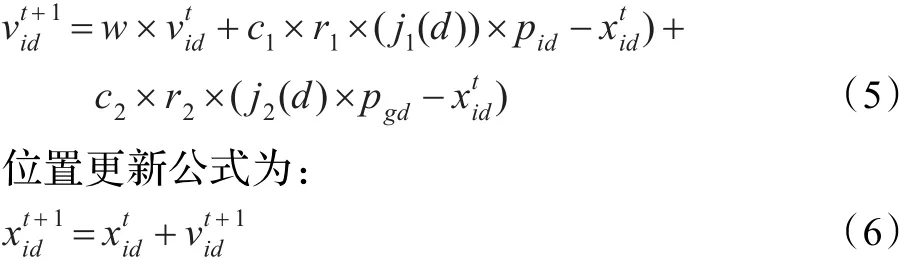
3 K均值聚类算法

MacQueen提出的K均值聚类算法主要用于数据对象的聚类，聚类产生的几组数据称为几个簇，聚类的过程就是使同簇中的对象的相似性尽可能达到最大，不同簇的对象间的数据差异性达到最大，进而分成不同的类。目前，聚类算法已应用于数据挖掘、模式识别和图像处理等许多领域，但同时K均值算法存在着以下缺点：（1）聚类结果好坏受到初始聚类中心的影响，不同的聚类中心可能产生不一样的聚类结果；（2）容易陷入局部最优，得到的聚类结果可能不是全局最优解。

算法的步骤：

（1）从S个数据对象中任意选择K个对象作为初始聚类中心。

（2）计算样本集中各个对象与这些聚类中心的距离，并根据最小距离进行划分，形成K个聚类域。

（3）计算各聚类域的中心点（每个聚类中所有对象的均值）。

（4）根据新的中心点对所有对象按照最小距离重新进行聚类划分。

（5）循环执行（3）到（4），直到每个聚类不再发生变化为止。

评价函数为：

式中，K是样本类数，xu是类m中数据样本的位置矢量，om是类m的中心点位置矢量，Um是类m中的数据样本。

4 基于扰动免疫粒子群和K均值的混合聚类算法

传统的基于粒子群的K均值聚类算法中，粒子的初始化方式是随机生成一组中心点，然后按照最近邻准则将数据进行聚类，再采用粒子群的寻优方式找到较优的粒子。该方法的缺点是随机生成的粒子中心点经常出现在数据的外围，导致运算效率降低。为提高粒子群算法的收敛效率，本文在初始读入数据集时，记录数据集各维的最大值和最小值，记第d维最大值xmaxd、最小值，然后在xmaxd和xmind之间随机生成数据中心点的第d维分量，粒子i编码结构记作：Xi(x11,x12,…,x1d,…,x1D,…,xm1,xm2,…,xmd,…,xmD,…,xK1,xK2,…,xKd,…,xKD),xmd∈[xmind,xmaxd]，其中xmd表示粒子i中数据的第m个聚类中心点的第d维分量，其中m∈1,2,…,K；d∈1,2,…,D；K为数据分类数，D为数据维度。

粒子群的聚类域编码结构记作：X(x11,x12,…,x1j,…,x1J;…;xl1,xl2,…,xlj,…,xlJ;…;xL1,xL2,…,xLj,…,xLJ),xlj∈[xminj,xmaxj]，其中，xl1,xl2,…,xlj,…,xlJ表示粒子群的第l个聚类域的中心点，xlj表示粒子群的第l个聚类域中心点的第j维分量，其中l∈1,2,…,L，j∈1,2,…,J；L为粒子聚类数，J为粒子编码结构的维度即J=K×D。

传统的粒子群算法中，惯性权重w的设置对算法的收敛结果有着很大的影响，w较大能够顺利地跳出局部最优解，w较小有利于算法收敛，本文采用的是基于适应度函数的自适应惯性调整方法[14]。

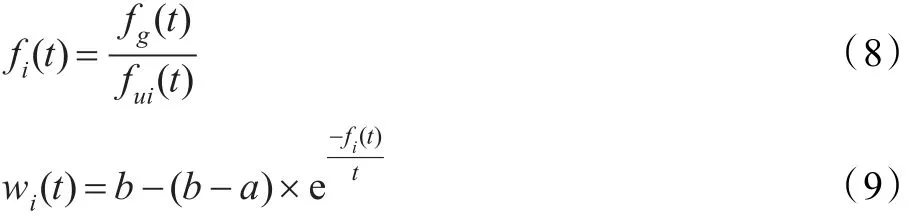
式中，t为当前迭代次数，a、b分别表示权值w的下限和上限，fg(t)为第t代粒子群的全局最优解的适应度值，fui(t)为第t代粒子i个体最优解的适应度值，fi(t)表示第t代粒子群的全局最优解与粒子i的个体最优解的适应度值比值。

随着迭代次数的增大，fui(t)逐渐趋近于fg(t)，因此fi(t)逐渐趋近于1，从而wi(t)逐渐趋近于a。

粒子趋同性是指所有的粒子在寻优过程中被全局最优粒子所吸引的特性，该特性导致群体的多样性大大降低，容易造成早熟收敛[13，15]。为此，学者们开始把免疫机制引入到粒子群算法中来，这在一定程度上提高了粒子摆脱局部极值的能力，但是这些算法提取的疫苗通常是以当前最优粒子的特征作为有效信息[16]，这仍然会导致大部分粒子向最好的粒子周围聚集，同样没有从根本上解决趋同性问题。为更好地解决该问题，本文算法中的免疫机制采用基于K均值的疫苗提取方法和基于个体浓度的免疫选择方法。在该算法中，一个粒子表示一组中心点，算法首先进行粒子群初始化和粒子寻优，再采用K均值算法对寻优后的粒子进行聚类，找到具有最高平均适应度值的聚类域，取该聚类域的聚类域中心及其最大半径作为疫苗的选择特征；然后根据该特征随机生成疫苗集，因此，该疫苗集具有较强的多样性；最后进行疫苗接种，并根据种群多样性保留机制对粒子进行免疫选择操作。

（1）疫苗的提取

步骤1根据数据各维的最大值和最小值随机生成一组中心点，每组中心点代表一个粒子，反复N次生成N个粒子。该粒子群经过迭代后生成N个较良个体群X，从X中选出较优的L个粒子作为初始聚类中心即：C1(0),C2(0),…,CL(0)。

步骤4采用K均值聚类算法更新各聚类域，设经过s次更新后，聚类域中心的变化幅度小于设置的阀值ε，此时的聚类中心记为：c1(s),c2(s),…,cL(s)。

步骤5选取具有最优平均适应度值的聚类域Ubest，使用该聚类域中心及其聚类域的最大半径构建疫苗。

该疫苗是K×D维向量，记作(q1,q2,…,qg,…,qK×D)，它的第g维分量qg是在[eg-hg,eg+hg]区间生成的一个随机数，g∈1,2,…,K×D。因此该疫苗集具有较优的适应度值和较好的多样性。

（2）疫苗的接种

算法先采用疫苗提取方法生成待用疫苗，然后判断是否满足粒子接种条件。若满足，则用该疫苗坐标取代原有的粒子坐标，反之则不进行接种。

粒子i的接种概率为：

式中，f(xi)为粒子i的适应度值。

首先针对每个粒子在（0，1）区间内各生成一个随机数，若接种概率大于该随机数，则进行接种，反之不接种。从数学角度分析可以看出，适应度值越大接种概率越大，但该方法并非绝对地对适应度值大的粒子进行接种，因此该方法在提高粒子群整体适应度的同时也保持了粒子群较好的多样性。然后对接受疫苗接种的个体进行免疫检测。即：若接种后的个体适应度值优于父代中所对应的个体，则接种成功，否则该个体被父代中所对应的个体取代。

（3）免疫选择

在该粒子群个体更新中，本文采用了以下种群的多样性保留机制，保证各个层次的适应值浓度都维持在一定的水平，防止适应值较优的粒子浓度过高，从而失去了适应值较差但有较好的进化趋势的粒子，导致粒子的多样性下降，使得算法容易陷入局部极值点。粒子i的免疫选择概率公式如下：

其中i=1,2,…,N，α、β为（0，1）的可调系数，用于调整粒子浓度和适应度值对免疫选择概率的影响程度。

算法的流程图如下：

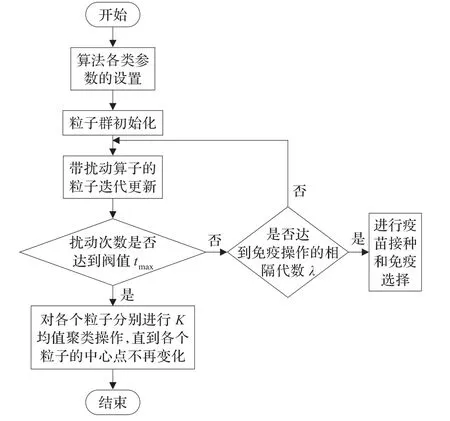
图1 基于扰动免疫粒子群和K均值的混合聚类算法流程图

算法各类参数的设置：记录聚类样本每一维的最大值和最小值：xmaxd和xmind，其中d=1,2,…,D。设置数据类别数K，粒子个数N、个体极值更新所需的连续停滞代数T1、免疫选择的可调系数α、β，全局极值更新所需的连续停滞代数T2、加权系数w的取值范围(a,b)、系数c1、c2，提取疫苗的相隔代数λ以及最大扰动次数阀值tmax。

粒子群初始化：根据样本每一维的最大值和最小值，在该范围内随机产生一组维数为D的初始数据即一个聚类中心，反复进行K次，生成K个初始聚类中心即一组中心点，将这组中心点作为一个粒子。然后根据这组中心点按最近邻准则将样本数据划分到K个聚类域中，用式（7）计算该粒子的适应值，同时作为该粒子的个体最优位置，初始化速度v，反复进行N次，共生成N个粒子。比较这些粒子的适应值和群体所经历的最好位置的适应值，并把全局最优粒子存入记忆库中。

带扰动算子的粒子迭代更新：粒子根据公式（5）、（6）采用自适应加权系数进行进化，更新各个粒子的各维分量，得到数据的新聚类中心，然后按照最近邻准则进行聚类划分，根据自适应度函数计算粒子的适应值，比较各粒子适应值，并及时更新全局最优值，并存入记忆库中。

5 实验结果及分析

实验环境：CPU i5 M460@2.53 GHz；内存2.0 GB；Windows 7操作系统；编译软件MATLAB 7.0。

本文采用常用于检验聚类算法效果的标准数据集：Iris、Wine、Breast cance、zoo、ionosphere。

数据集的详细信息如表1所示。

表1 原始数据信息

对于标准数据集，正确率是评价聚类算法好坏的重要指标，本文算法分别对数据集Iris、Wine、breastCancer、zoo、ionosphere进行20次测试，计算20次的平均正确率，并与K-means算法、PSO+K-means算法、K-medians[17]算法、K-medoids[7]、文献[6]算法进行比较。

本实验参数确定方法如下：

首先根据参考文献[18]选取权重系数区间为（0.1，0.9）即a、b分别为0.1和0.9；根据参考文献[19]的结论，选取学习因子c1、c2分别为2和2.5；根据学术经验选取粒子数为20、最大扰动次数为80、免疫选择的可调系数α、β均为0.5、个体极值和全局极值最大停滞步数均为5、疫苗提取相隔代数10；然后，在其他参数不变的情况下逐个改变根据学术经验选取的参数设置，直到取得相对较好、较稳定的实验效果，此时该参数确定为初步实验参数；最后采用初步实验参数进行测试，根据实验效果对各参数进行微调，以获得更优的聚类效果，此时的参数确定为最终试验参数。

经确定，实验参数权重w的范围a、b分别为0.1和0.9、c1、c2为2和2.5、最大扰动次数30，粒子数30，个体极值最大停滞步数和全局极值最大停滞步数均为3、提取疫苗的相隔代数8、免疫选择的可调系数α、β分别为0.3、0.7，实验结果如表2所示。

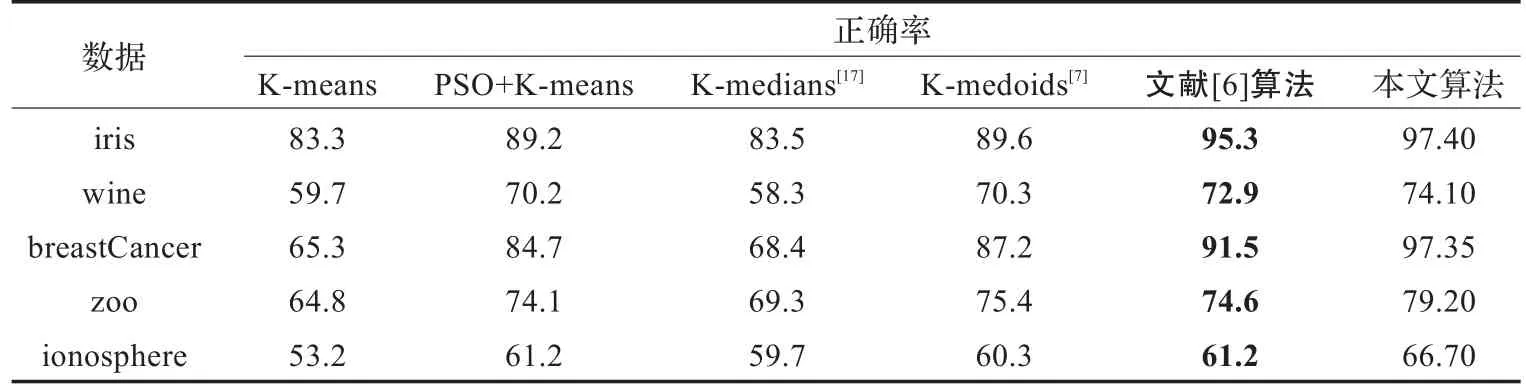
表2 各算法的聚类结果（%）

从表2可以看出，基于扰动免疫粒子群和K均值的混合聚类算法的聚类结果优于其他算法。

为检验该聚类算法的稳定性，采用以上算法对Iris和zoo数据集进行测试，连续运行50次，并记录最优解出现次数和迭代次数，计算出各算法收敛的平均迭代次数，记最好实验结果的正确率为最好正确率，最差实验结果的正确率为最差正确率，50次试验结果的平均值为平均正确率，采用方差公式计算该50次实验正确率的方差。各算法对Iris和zoo数据集的测试结果如表3、表4所示。

表3 各算法对Iris数据集的正确率比较

从表3、表4可以看出，和其他算法相比，本文算法的平均正确率较高，出现最优解的次数较多，正确率方差最小，且平均迭代次数较少。因此，该算法的聚类效果较好，收敛结果比较稳定。

该算法对zoo数据集的收敛曲线如图2所示，对iris数据集的收敛曲线如图3、图4、图5所示。

从表4可以看出本文算法对zoo数据集的收敛最稳定，50次实验找到的最优解相同，从图2可知，该收敛曲线比较平滑，经过多次扰动没有找到更优的收敛结果。

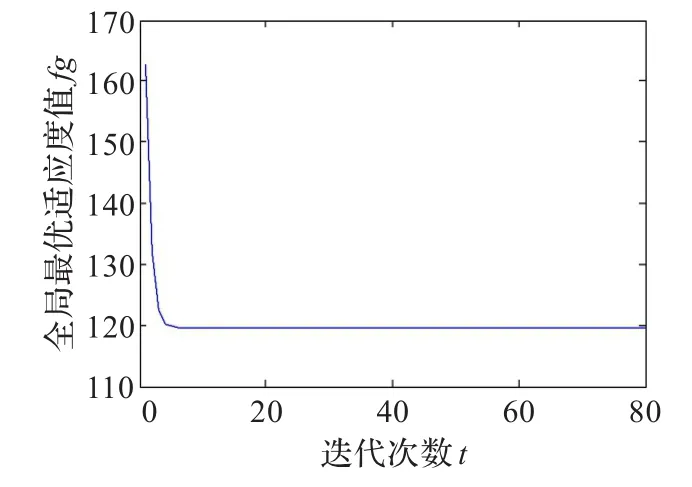
图2 zoo数据集收敛曲线图

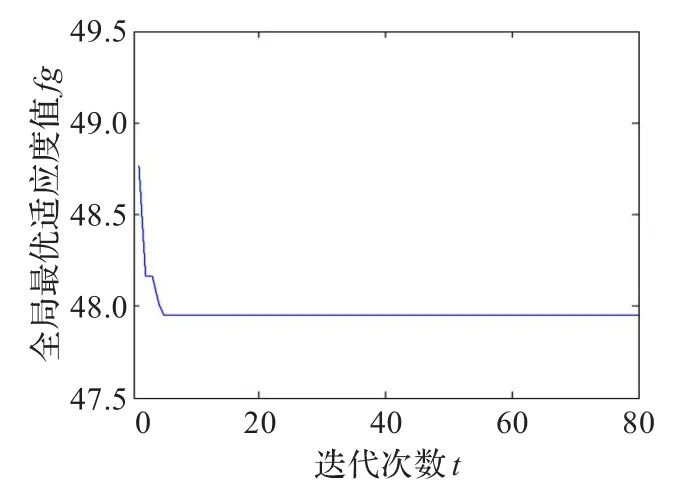
图4 iris数据集收敛曲线图

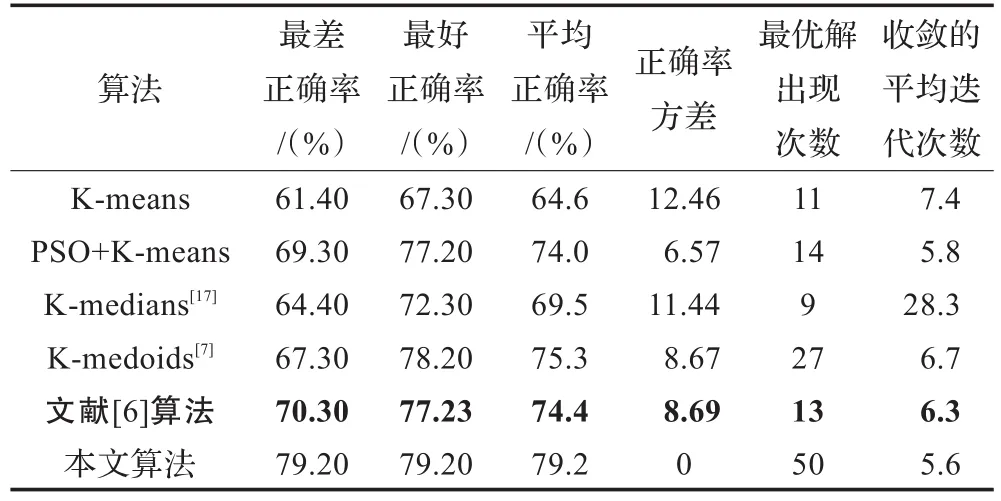
表4 各算法对zoo数据集的正确率比较

图3、图4、图5是该算法对iris数据集测试时出现的三种典型的收敛曲线图。从图3可知，该收敛曲线比较平滑，较容易找到了较优解，寻优过程最顺利。从图4可知，本次收敛的起始全局最优适应度值为48.77，迭代到第2次时，全局最优解的进化出现停滞，到第3次迭代时算法找到了适应度值为47.955的较优解。从图5可知，算法的起始全局最优适应度值为48.21，算法迭代到第3次时陷入局部最优，到第12次迭代时算法跳出局部最优，从迭代次数可知，本次收敛从陷入局部最优到跳出局部最优共经历了3次扰动，通过第3次扰动才找到适应度值为47.98的较优解，此时，算法再次陷入局部最优，通过4次扰动才找到适应度值为47.955的较优解。

6 结语

本文针对K均值聚类算法对初始聚类中心的高敏感性、算法容易陷入局部最优解等问题提出基于扰动免疫粒子群和K均值的混合聚类算法。该算法的疫苗集具有较强的多样性和较高的平均适应度值，并采用了基于浓度和适应度值的免疫选择策略，使该算法在一定程度上提高了粒子的多样性；同时，扰动算子的引入极大地提高了算法的遍历性和算法跳出局部最优解的能力。最后，对各个粒子进行K均值操作，提高收敛精度。实验证明，该算法聚类效果较好，且比较稳定。

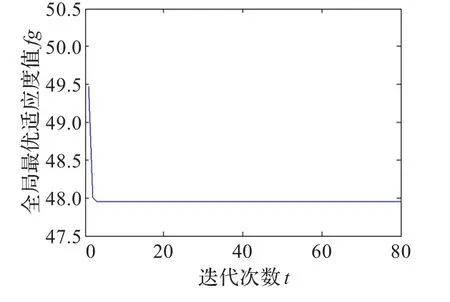
图3 iris数据集收敛曲线图

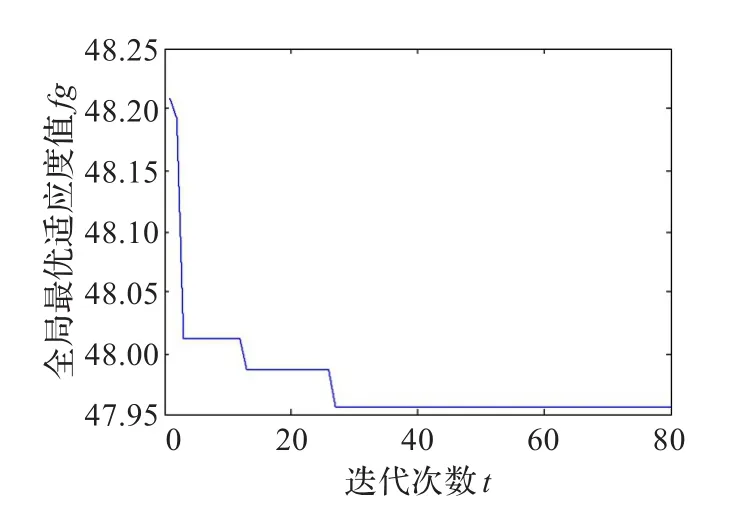
图5 iris数据集收敛曲线图

[1]Krishma K，Murty M N.Genetic Kmeans algorithm[J]. IEEETransactionsonSystem，ManandCybernetics，Part B，1999，29（3）：433-439.

[2]Maulik U，Bandyopadhay S.Genetic algorithm-based clusteringtechnique[J].PatternRecognition，2000，33（9）：1455-1465.

[3]孟伟，韩学东.蜜蜂进化型遗传算法[J].电子学报，2006，34（7）：1294-1300.

[4]郑晓鸣，吕士颖，王晓东.免疫接种粒子群的聚类算法[J].电子科技大学学报，2007，36（6）：1264-1267.

[5]陶新民，徐晶，杨立标，等.一种改进的粒子群和K均值混合聚类算法[J].电子与信息学报，2010，32（1）：92-97.

[6]姚丽娟，罗可，孟颖.一种基于粒子群的聚类算法[J].计算机工程与应用，2012，48（13）：150-153.

[7]马箐，谢娟英.基于粒计算的K-medoids聚类算法[J].计算机应用，2012，32（7）：1973-1977.

[8]盘俊良，石跃祥，李娉婷.一种新的粒子群优化聚类方法[J].计算机工程与应用，2012，48（8）：179-181.

[9]于海涛，贾美娟，王慧强，等.基于人工鱼群的优化K-means聚类算法[J].计算机科学，2012，39（12）：60-64.

[10]熊忠阳，陈若田，张玉芳.一种有效的K-means聚类中心初始化方法[J].计算机应用研究，2011，28（11）：4188-4190.

[11]沈明明，毛力.融合K-调和均值的混沌粒子群聚类算法[J].计算机应用研究，2011，47（27）：144-151.

[12]Kennedy J，Eberhart R C.Particle swarm optimization[C]// Proc of the IEEE International Conference on Neural Networks.Pisataway，NJ：IEEEServiceCenter，1995：1942-1948.

[13]Clerc M，Kennedy J.The particle swarm-explosion stability and convergence in amultidimensional complex space[J]. IEEE Transactions on Evolutionary Computation，2002，6（1）：58-73.

[14]廖子贞，罗可，周飞红，等.一种自适应惯性权重的并行粒子群聚类算法[J].计算机工程与应用，2007，43（28）：166-168.

[15]Senthil A M，Ramana M G，RaoM V C.A novel effective particle swarm optimization like algorithm via extrapolation technique[C]//2007 International Conference on Intelligent and Advanced Systems，2007.

[16]行小帅，霍冰鹏.基于免疫的并行单亲遗传算法研究[J].通信学报，2007，28（8）：99-104.

[17]Har-Peled S，Kushal A.Smaller coresets for k-median andk-meansclustering[J].DiscreteandComputational Geometry，2006，37（1）：3-19.

[18]吕振肃，侯志荣.自适应变异的粒子群优化算法[J].电子学报，2004，32（3）：416-420.

[19]Bezdek J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York：Plenum Press，1981.

XU Junwei,XU Weihong

School of Computer and Communication Engineering,Changsha University of Sciences and Technology,Changsha 410114,China

After analyzing the disadvantages of initialization sensitive and local extremum of the K-means algorithm,this paper proposes a hybrid clustering algorithm based on disturbance immune particle swarm optimization and K-means. The new clustering algorithm uses K-means to divide the particles into several categories and then chooses the optimal clustering domain to produce vaccine.After that,it adopts the vaccination and immune selection to improve the diversity of the particles.Meanwhile,in the algorithm,the disturbed arithmetic operators is introduced to break away from the local extremum by changing the movement of the particles when the times of the continuous stagnation exceed the threshold. The K-means clustering algorithm is employed to improve the convergence precision of the algorithm when the times of the disturbance meets the maximum.The experimental results show that the convergence accuracy and stability of the algorithm are good.

particle swarm optimization algorithm;K-means clustering algorithm;vaccination;immune selection

针对传统K均值聚类算法对初始化敏感和容易陷入局部最优的缺点，提出了一种基于扰动免疫粒子群和K均值的混合聚类算法。该算法采用K均值将粒子群进行分类，选择平均适应度值最高的聚类域用于产生疫苗，在粒子更新过程中采用疫苗接种机制和免疫选择机制提高粒子的多样性。当个体极值和全局极值连续停滞代数超过所设置的阀值时，算法使用扰动算子改变粒子群的运动方向，提高算法跳出局部极值的能力。当扰动次数达到设置的最大值时，对各个粒子进行K均值操作，提高收敛精度。实验结果表明，该算法具有较高的正确率和较好的稳定性。

粒子群算法；K均值聚类算法；疫苗接种；免疫选择

A

TP391.4

10.3778/j.issn.1002-8331.1401-0440

XU Junwei,XU Weihong.Hybrid clustering algorithm based on disturbance immune particle swarm optimization and K-means.Computer Engineering and Applications,2014,50（22）：163-169.

湖南省科技计划项目（No.FJ3005）。

许竣玮（1986—），男，硕士，研究领域为智能信息处理；徐蔚鸿（1963—），男，教授，博士生导师，主要研究领域为人工智能及应用、机器学习、图像处理与模式识别。E-mail：328214680@qq.com

2014-01-25

2014-03-17

1002-8331（2014）22-0163-07

CNKI网络优先出版：2014-06-04,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0440.html