结合SOM的关联规则挖掘研究

景波，刘莹，陈耿

南京审计学院信息科学学院，南京 210029

结合SOM的关联规则挖掘研究

景波，刘莹，陈耿

南京审计学院信息科学学院，南京 210029

1 引言

随着数据库应用技术的快速发展，许多企事业单位积累了海量的、以不同形式存储的数据资源，因此与之相应的审计活动对信息化水平的要求也在不断提高。目前，联网实时审计已成为审计信息化发展的重点，在联网审计的海量数据环境下，如何根据需要智能和自动地找出有用的信息并发现审计线索，是联网实时审计中迫切需要解决的问题[1]。审计署从2004年开始收集并整理审计专家经验库，经过近十年的建设，其内容涉及领域广泛、审计方法全面详实，通过对它进行多维分析和数据挖掘等技术手段，可以提取出大量有价值的规则。这些规则可以成为联网审计活动中进行自动化评价及预测的基础和依据。

笔者参加的“某集团工程联网审计”项目中，海量数据间的关系错综复杂，审计线索难以发现。笔者思索通过数据挖掘对被审单位数据和审计专家经验库进行关联规则快速提取；再利用自组织神经网络相似聚类方法对审计专家经验库抽取的规则划分出相似规则群；通过对被审单位关联规则集合和专家经验的相似规则群进行相对强弱、趋近率和价值率的比较最终得到审计线索集合，其流程如图1。

2 算法思想

关联规则挖掘用于发现大量数据间的相互关系，它和自组织神经网络都属于典型的无监督学习模式[2]。在经典的关联规则Apriori算法中，首先搜寻数据中所有符合最小支持度（Support）的最大项目集（Itemset），再利用此最大项目集产生相关规则[3-4]。算法缺点是对数据库I/O访问过频繁，产生过多的候选项目集。后期Park等提出的DHP算法由于哈希方式会产生碰撞，实际扫描次数与Apriori算法相近；Brin等提出DIC算法，算法中区段大小的划分成为执行效率的瓶颈；Savasere等提出Partition算法，其分块大小要配合主存储器的大小。本文提出以分解法为基础的快速匹配关联规则挖掘算法（FMA），算法目标不是寻找最大项目集，而是寻找最适当的项目集，即k＜n[5]。

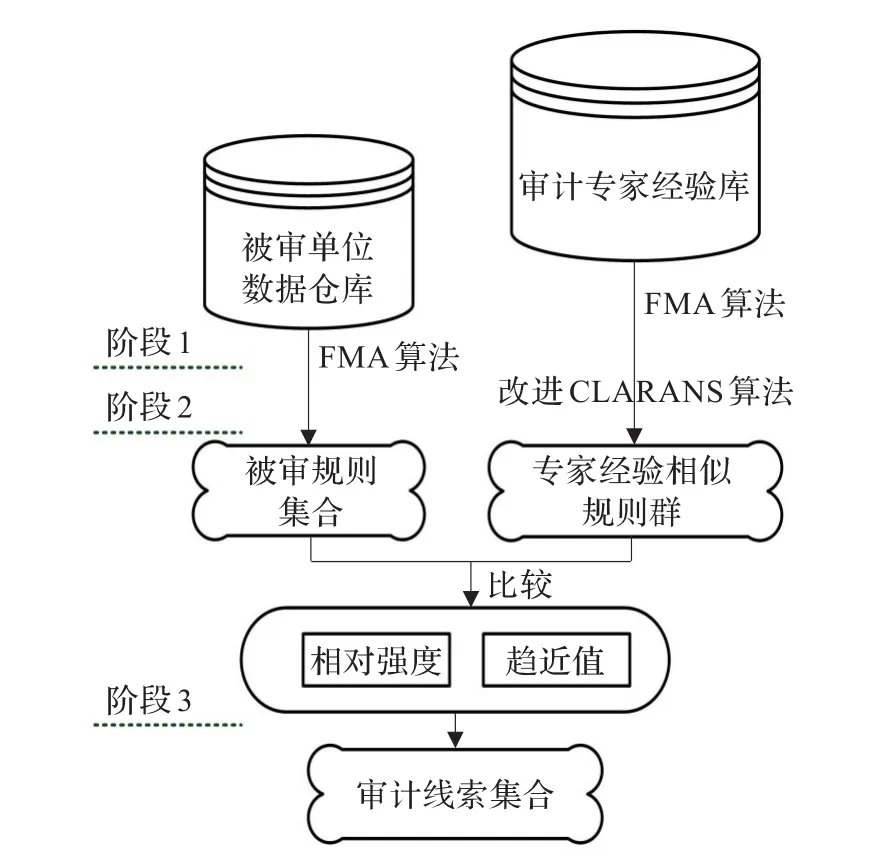
图1 审计线索智能发现流程图

专家经验相似规则群的获得采用SOM中的经典CLARANS算法[6]为原型的改进算法，CLARANS算法采用随机方式产生初始节点，然后不断为当前节点寻找总代价更小的邻近节点来改善聚类结果；随机产生初始节点对总搜索次数影响较大，差的初始节点将会增加搜索邻近节点过程中邻近节点替换和探索的总次数[7-8]。本文改进了CLARANS算法，为优化初始节点的选择，增加了初始节点预聚类的方法，具体流程为：

（1）扫描数据集合，计算在数据空间中数据对象各维的分布因子，并将结果按降序进行排列。

（2）选分布因子最大的m维，并生成相应m维的子数据空间S。

（3）将数据空间S划分成m维的网格，每个网格称为一个m维的网格对象。

（4）再次扫描数据集合，按m维的值将数据划分到相应的网格中；以网格中的数据对象个数作为网格对象权重，以数据对象的均值作为网格对象的值。

（5）在子数据空间S中，在所有网格对象上使用加权距离产生k个初始中心点。

（6）使用第5步中得到的k个中心点作为CLARANS算法中的初始节点。

3 算法实现

3.1 快速匹配关联规则挖掘算法思路

快速匹配关联规则挖掘算法（FMA），利用分解法将每笔交易数据分解成长度为k的项目集(k＜n)；在各长度相同的项目集里，取各项目集的项目集值（即支持度的乘积）最大值者，称为最大项目集(max_itemse)。在每笔交易中，找出不同长度的最大项目集，再比较其包含、相等的隶属关系，找出最大的集合；最后得到不同长度的项目集的集合。

3.2 计算相似规则群

利用自组织映射神经网络中的聚类分析的CLARANS算法的改良，来进行相似规则群的划分。CLARANS算法即根据数据分群的原则，将数据依相近似的程度予以分群，使各群内的数据相近似度最高，而群外的相近似度减至最低。其最主要的作用是在各群组内建立有意义的数据分群。同时，为优化初始节点的选择，增加了预处理的方法。

首先，C记为T的交易向量，矩阵V记作交易向量C的集合，定义如下：

利用CLARANS改良算法将数据按照相近似度分为数个群聚，每个相似性群聚，即代表着该群聚的属性聚集，其中的每个属性的先后顺序也代表该群聚内各属性的重要程度。算法描述：

至此，已经得到了由第一阶段FMA算法产生的关联规则集合和第二阶段相似规则群的集合，对两个集合进行相对强弱、趋近率和价值率的比较即可得到最终目标集合。具体合并算法由于篇幅所限，不在此展开讨论。

4 实验分析

为检验算法效率，在IBM（IBM，2003）的数据产生器生成的数据环境中进行与Apriori、FP_Tree算法的比较测试。实验主机为Pentum4-2.8 GHz，1 GB Mem，运行在Borland Jbuilder9平台上，使用JAVA语言编写算法。

实验数据为5 000、10 000、25 000、50 000、100 000及200 000六种，数据的交易长度平均为10，最小支持度选为0.005或0.007 5。在minsup不变，而交易量逐渐由5 000增加至200 000时，其FMA、Apriori与FP_Tree之执行时间的对比如图2。在交易量固定为5 000或200 000时，而minsup值从0.02逐渐减少至0.005时，其FMA、Apriori与FP_Tree之执行时间的对比如图3。

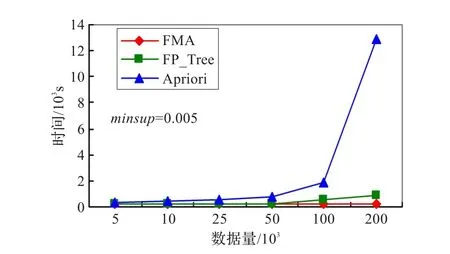
图2 minsup=0.005&交易量递增时执行时间对比

在此实验里，从整体来看，FMA与Apriori的比较里，最小的差距是数据为5 000，minsup为0.02时，FMA为Apriori的9.09%；最大的差距是数据为200 000，minsup为0.005时，执行时间FMA为Apriori的0.45%。在FMA与FP_Tree的执行时间里，最小的差距是数据为50 000，minsup为0.02时，执行时间FMA为FP_Tree的71.43%；最大的差距是数据为10 000，minsup为0.005时，执行时间FMA为Apriori的8.11%。

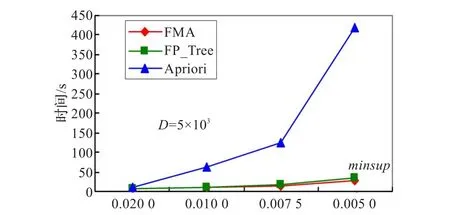
图3 D=5 000 minsup递减时执行时间对比

在不同数据集规模的情况下，设目标群个数为5，局部最优解个数为2，最大邻居数为100，CLARANS与改良算法的平均运行时间对比如图4，邻居节点替换总代价的平均次数对比如图5。

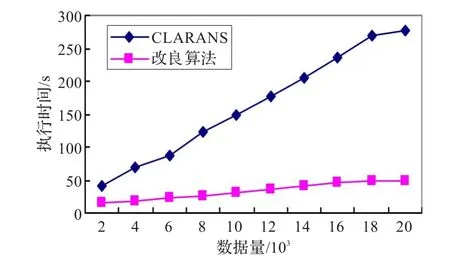
图4 不同数据量下执行时间对比

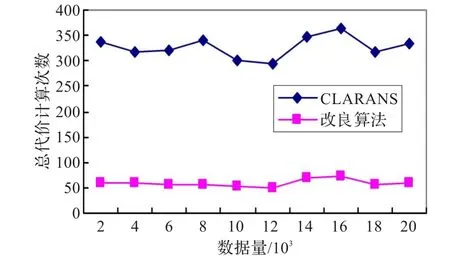
图5 不同数据量下替换总代价对比

从图中可以看出，在目标群数值固定的情况下，随着数据量增加，CLARANS和改良算法的运行时间都会随之增加，但改良算法的增长较缓慢，并且执行时间仅为CLARANS算法的1/5，邻居节点数随数据增加变化不大，改良算法的计算量也仅为原算法的1/5。

5 结束语

本文以FMA算法将被审单位的海量数据利用数据挖掘手段，找出适当长度的项目集；同时通过自组织特征映射神经网络的CLARANS算法产生项目集（专家经验相似群）；使用相对强弱、趋近率、价值率等集合操作手段，产生得出审计目标线索群。实验表明，算法能做到快速生成审计规则及形成审计线索群，符合预期设想。下一步将通过实际审计过程中的问题发现，做进一步的评估与验证。

[1]刘家义.加快审计信息化建设的思考[J].中国审计，2000（9）：4-8.

[2]国家863计划审计署课题组.计算机审计数据采集与处理技术研究报告[R].北京：清华大学出版社，2006.

[3]张怀亭，王忠民.提高关联规则完整性和有效性的算法[J].计算机工程与应用，2003，39（29）：208-210.

[4]马盈仓.挖掘关联规则中Apriori算法的改进[J].计算机应用与软件，2004，21（11）：82-84.

[5]景波，刘莹，黄兵.基于审计的时态关联规则研究[J].微计算机信息，2007（18）：176-178.

[6]田景文，高美娟.人工神经网络算法研究及应用[M].北京：北京理工大学出版社，2006.

[7]张书春，孙秀英.基于网格结构的CLARANS改进算法[J].计算机工程，2012（6）：56-59.

[8]Zhang Yaping，Sun Jizhou，et al.Parallel implementation of CLARANS using PVM[C]//Proceeding of the 3rd International Conference on Machine Learning and Cybernetics，2004：26-29.

[9]姜华，孟志青，周克江，等.一类时态近似周期关联规则的知识发现问题[J].计算机工程与应用，2010，46（20）：241-244.

[10]Meng Zhi-qing.Study of temporal type and time granularityinthetemporal datamining[J].Natural Science Journal of Xiangtan University，2000，22（3）：1-4.

[11]Meng Zhiqing.Knowledge discovery for a kind of neighbor temporalassociatedrules[J].PatternRecognitionand Artificial Intelligence，2001，14（4）：458-462.

[12]Jiang Hua，Meng Zhiqing.Study of data mining for a kind of temporal approximate periodicity[J].Computer Engineering，2006，32（22）：61-63.

[13]Li Y，Ning P，Wang X S，et al.Discovering calendar-based temporal association rules[J].Data and Knowledge Engineering，2003，44（2）：193-218.

[14]Yang Jiong，Wang Wei，Yu P S.Mining asynchronous periodic patterns in time series data[J].IEEE Transactions on Knowledge and Data Engineering，2003，15（3）：613-628.

[15]马春玲，李廉.基于等价关系的关联规则的挖掘[J].兰州大学学报：自然科学版，2002（4）：64-71.

JING Bo,LIU Ying,CHEN Geng

School of Information Science,Nanjing Audit University,Nanjing 210029,China

In order to achieve the audit trail of the massive data quickly found through data mining FMA algorithms to quickly extract trial data and audit expertise library association rules；re-use of self-organizing neural network improved CLARANS algorithm to extract audit expertise library divide a similar rule base rules；then by trial set of association rules and expert experience similar rules group relative strength,the approach value and the different rate of comparing the resulting set of audit trail.

association rule mining;Self-Organizing Map（SOM）;audit trail

为了实现在海量数据中的审计线索的快速发现，通过数据挖掘FMA算法对被审数据和审计专家经验库进行关联规则快速提取；再利用自组织神经网络改良CLARANS算法对审计专家经验库抽取的规则划分出相似规则群；然后通过对被审单位关联规则集合和专家经验的相似规则群进行相对强弱、趋近率和价值率的比较，最终得到审计线索集合。

关联规则挖掘；自组织神经网络；审计线索

A

TP311

10.3778/j.issn.1002-8331.1212-0298

JING Bo,LIU Ying,CHEN Geng.Research on association rule based on SOM.Computer Engineering and Applications,2014,50（22）：154-157.

江苏省公共工程审计重点实验室开放课题（No.20201201213）；江苏省审计信息工程重点实验室开放课题（No.AIE201205）；国家自然科学基金（No.70971067，No.71271117）。

景波（1975—），男，副教授，主要研究方向：IT审计，数据挖掘；刘莹（1977—），女，讲师，主要研究方向：数据挖掘，分布式计算技术；陈耿（1965—），男，教授，博士，主要研究方向：数据挖掘，审计信息化，知识工程等。E-mail：jbo@nau.edu.cn

2012-12-25

2013-02-25

1002-8331（2014）22-0154-04

CNKI网络优先出版：2013-03-13,http://www.cnki.net/kcms/detail/11.2127.TP.20130313.0955.024.html