基于稀疏预处理和循环观测的语音压缩感知
2014-08-03徐皓波于凤芹
徐皓波,于凤芹
江南大学 物联网工程学院,江苏 无锡 214122
基于稀疏预处理和循环观测的语音压缩感知
徐皓波,于凤芹
江南大学 物联网工程学院,江苏 无锡 214122
1 引言
Donoho提出的压缩感知理论突破了奈奎斯特采样定理的局限,只要要求信号在时域或变换域上具有稀疏性,通过一个观测矩阵将原始的高维信号投影到低维空间上,由低维的观测信号利用恢复算法就能以高概率重构出原始信号,实现一种采样与压缩同时进行的过程[1]。观测矩阵与信号稀疏基之间的非相关性越强,由观测精确重构原信号的几率就越大[2],因此在压缩感知中大部分采用具有高度非相关特性的高斯随机矩阵作为观测矩阵,但由于高斯随机矩阵的每个元素是独立的随机数,因而产生复杂、计算存储量大。Candes提出了一种部分傅里叶矩阵作为观测矩阵来代替高斯随机矩阵[3],但由于傅里叶基仅与时域或频域稀疏的信号不相关,其应用范围受到限制[4]。文献[5]从理论上分析了结构化的Toeplitz和循环矩阵恢复稀疏信号的效果证明其作为观测矩阵的可行性。文献[6]针对语音信号在DCT域能显示出近似的稀疏性提出语音信号DCT域压缩感知。文献[7]在语音信号DCT域压缩感知的基础上提出帧间和帧内两种自适应方法确定观测个数,在一定的重构误差下能保证更低的压缩率。文献[8]利用语音本身构造了一种自相关观测矩阵进行观测,同等重构性能下压缩率比高斯随机矩阵更低。
本文以语音信号为研究对象,就语音信号在DCT域近似稀疏的问题,提出在观测前做一个将信号的DCT域小系数在一定阈值下置零后反变换回时域的预处理工作,得到在DCT域真正稀疏的一个近似信号,把它作为新的对象进行观测。基于快速傅里叶变换原理使用傅里叶变换矩阵构造得到循环观测矩阵进行观测投影,并计算其与DCT基的互相关系数证明其非相关性能够替代高斯随机矩阵,且循环观测矩阵存储矩阵元素更少。最后利用OMP正交匹配追踪[9]方法对观测信号进行恢复。仿真实验对比了一帧语音信号在四种压缩率下循环观测矩阵同高斯随机矩阵的重构情况,并研究了不同压缩率下各帧信噪比情况。
2 基于稀疏预处理和循环观测的语音压缩感知
2.1 压缩感知基本原理
假设信号 x=[x(1),x(2),…,x(N)]T∈RN可以用 N 维的基向量的线性组合表示,由可以形成一个 N×N 的基矩阵 Ψ=[ψ1,ψ2,…,ψN],信号 x 就可以表示成:域的表示。如果Θ中只有K个是非零的,且K≪N,那么原信号就可以只由K个基向量的线性组合构成,说明信号x是K稀疏的。假设Φ为一个M×N维的观测矩阵(M<N),长度为N信号通过Φ的投影得到了M个观测值,记为 y=(y1,y2,…,yM),即 y=Φx=ΦΨΘ 。因为 M<N,由 y求出Θ是一个欠定问题,无确定解。但是如果Θ足够稀疏,且观测矩阵Φ同信号稀疏基Ψ不相关就能得到一个确定解,在观测数目M≥4K的前提下可以利用一系列优化算法求解出信号x的稀疏系数向量,然后进一步得到原信号。重构信号最直接的方法就是通过l0范数解决下式这个最优化问题:

得到稀疏系数向量的估计。求解最小l0范数是一个NP难问题,可以利用BP基追踪和OMP正交匹配追踪等方法进行求解。
2.2 DCT域稀疏性
在对语音信号进行压缩感知处理时,由观测信号恢复原信号极大地依赖信号变换后的稀疏性。信号在变换域越稀疏,恢复的精度越高。由于语音信号具有类似余弦信号的周期特性,因此可以用DCT离散余弦变换来表示语音信号如下:
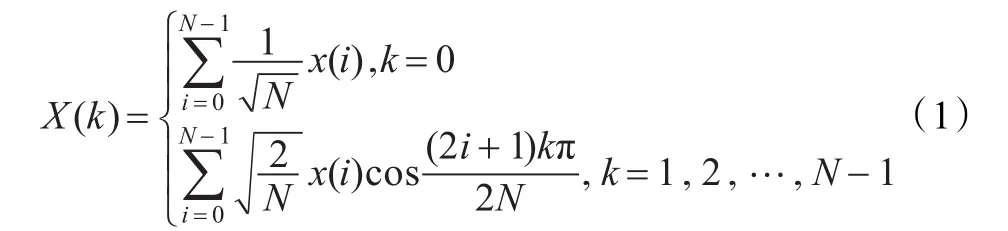
经过DCT变换后的稀疏系数为:
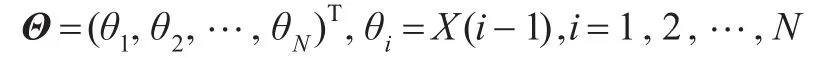
则语音信号可表示为 x=ΨΘ,Ψ为离散余弦基矩阵。语音信号在DCT域是近似稀疏的,系数向量中含有大量的非零小系数,为此本文提出将语音信号先在DCT域进行稀疏预处理的改进:将信号的DCT域小系数在一定阈值下置零后反变换回时域,以此改善变换域的稀疏性。
2.3 循环观测矩阵的构造
循环矩阵的基本形式具有如公式(2)的特征。由于循环矩阵的特殊结构,循环矩阵与信号的乘积y=Cx相当于计算循环矩阵首列向量与信号的离散循环卷积y=A⊗ x,A={a0,a1,…,aN-1},所以只需存储矩阵的一列元素就能获得矩阵全部的信息,计算观测值也只需计算一次循环卷积,大大节省了存储计算成本。构造一个N×N维的循环矩阵可以由傅里叶变换矩阵F如公式(3)和对角阵 Λ=diag(λ)通过C=F-1ΛF 得到[10]。
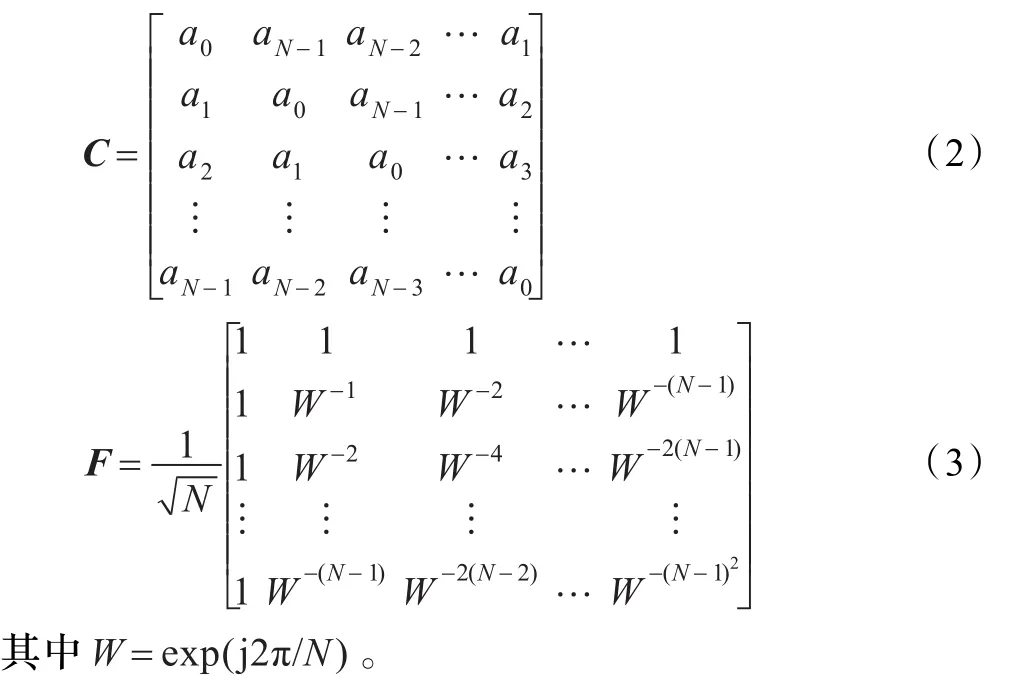
在压缩感知理论中,观测矩阵是M×N维的,所以必须从N×N维的循环矩阵中抽取M行组成观测矩阵。通过观察矩阵结构发现,循环矩阵与同样尺寸的高斯随机矩阵相比拥有少得多的可变参数,循环矩阵本身的随机性并不强。
为了说明循环观测矩阵同样可以应用于对语音信号的压缩感知,这里可以提出观测矩阵Φ与变换基矩阵 Ψ 之间的互相关系数 μ(D),D=ΦΨ=[d1,d2,…,dK]来衡量其非相关性能,定义如下:

μ(D)的值在(0,1)之间,其值越接近于0表明观测矩阵Φ与变换基矩阵Ψ之间就越不相关,观测矩阵的性能就越好,由观测恢复的信号也越精确。
2.4 OMP重构
OMP正交匹配追踪方法是MP算法的改进,本文利用它求解最小l0范数得到稀疏系数向量Θ的估计。MP算法的主要思想是从过完备的原子库中通过计算信号与原子的内积选择一个与内积最大的原子,该原子与待分解信号最为匹配,从而构建一个稀疏逼近,并求出信号残差,然后继续选择与信号残差最匹配的原子,反复迭代,若残差值在可以忽略的范围内原信号可以由这些原子来线性近似表示。OMP算法以MP为基础在分解的每一步对所选择的全部原子进行正交化处理,这使得在精度要求相同的情况下其收敛速度更快。在利用OMP方法进行压缩感知重构时,待分解信号就是观测信号 y,原子库为 D=ΦΨ,由估计得到稀疏系数向量Θ^还原的时域信号x^就是重构信号。

图1 实现总流程图
3 实现步骤
本文基于稀疏预处理和循环观测的汉语语音压缩感知实现如图1。
详细描述如下:
(1)首先将语音信号进行DCT域稀疏预处理,包括DCT变换、阈值置零和IDCT反变换,阈值可以设置为固定值,也可以根据变换域系数分布设置动态值。预处理使信号在DCT域绝对稀疏,同时也得到变换域上的非零个数K。
(2)由傅里叶变换矩阵F通过公式C=F-1ΛF得到一个N×N维循环矩阵,对角阵各元素呈随机分布。再从N×N维方阵中随机抽取M行构成M×N维的矩阵,该矩阵就是构造得到的循环观测矩阵。
(3)经过稀疏预处理后的信号 x′在循环观测矩阵Φ下进行观测投影得到观测值y。
(4)由观测信号 y进行OMP重构初始化阶段:信号残差r0=y,原子索引集合为空,过完备原子库为D=ΦΨ。
(5)计算残差与过完备原子库每列dj的内积,记录内积最大的那列所对应的列数
(6)更新原子索引 Λt=Λt-1∪{λt},存储挑选出来的重建原子集合Dt=[Dt-1,dφ],并在 D 中剔除该列。t
(9)判断是否跳出循环,若循环次数t>K则停止迭代,否则继续执行残差与过完备原子库内积计算。
(10)由得到的系数向量得到重构语音信号x^=ΨΘ^。
4 仿真实验与结果分析
4.1 DCT域稀疏性分析及阈值选取
仿真实验对象为男声发音为“大衣”采样率16 kHz的汉语语音信号,本节首先对一个语音帧(N=512)的DCT域系数分布进行分析,如图2所示。
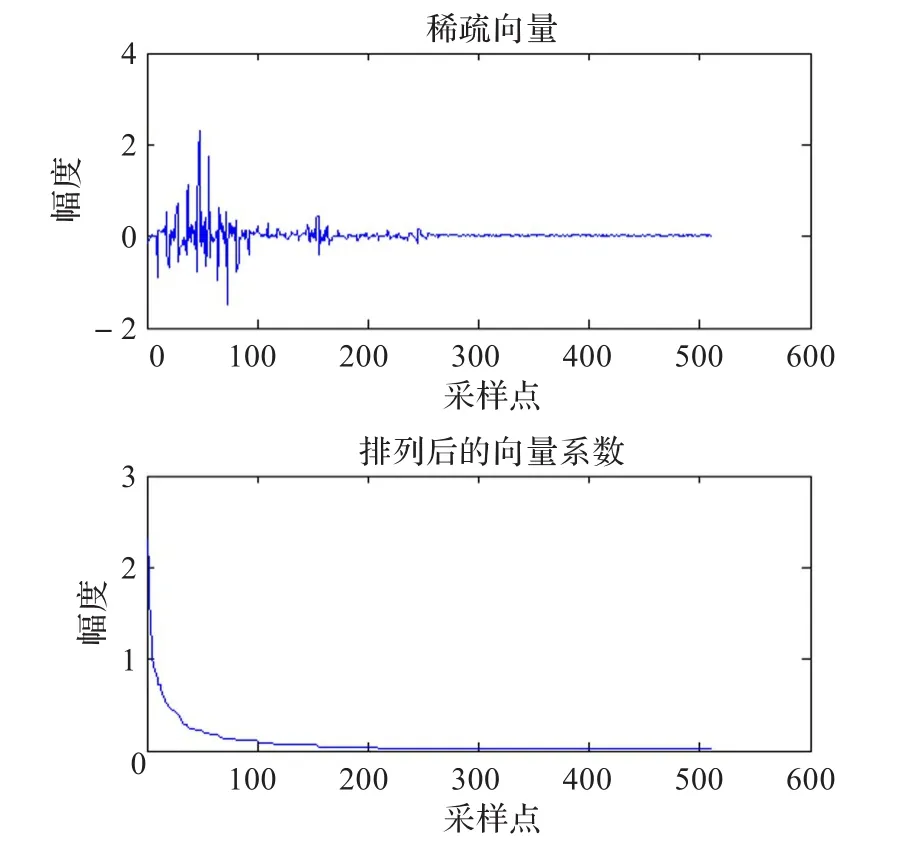
图2 DCT域系数分布及其降序排列
观察系数向量发现语音信号在DCT域并不是绝对稀疏而是近似稀疏,系数向量中含有大量的非零小系数,将那些趋近于零的系数置零,反变换得到一段在DCT域绝对稀疏的语音信号。由于各帧的能量分布不同,其DCT域系数向量能量亦有差别,所以并不能对每帧统一阈值。并且阈值设置过低信号非零元个数K不满足N>M≥4K稀疏性则达不到要求,设置过高重构精度则不理想。观察分布可以发现其大系数幅值集中于低频的前半帧,为此这里取前300个采样点的平均值作为DCT域置零阈值:

这样不同语音帧会根据自身变换域系数分布确定出一个动态阈值,同时也方便统计出系数中的非零个数。表1给出了阈值选取与稀疏性、信号精度的关系。
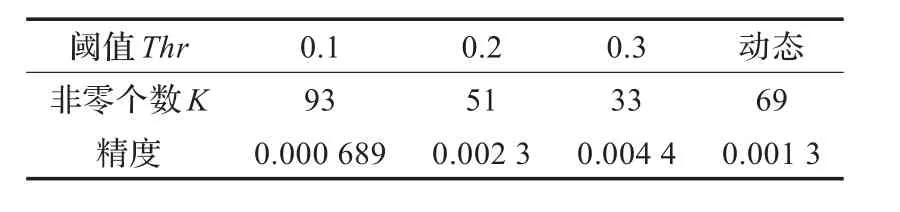
表1 阈值选取与稀疏性、信号精度的关系
4.2 循环观测矩阵非相关性分析
本节使用互相关系数来衡量循环观测矩阵对于DCT基的非相关性,并同高斯随机矩阵和傅里叶矩阵进行对比。循环矩阵I由随机产生的第一列循环得到;循环矩阵II是由傅里叶矩阵根据公式C=F-1ΛF得到,其特征值为±1的对称伯努利随机分布;循环矩阵III同II的构造类似,其特征值为复平面的单位球分布。然后再从N×N维的循环矩阵中随机抽取M行构成M×N维的观测矩阵。表2给出了三类循环矩阵与高斯随机矩阵及傅里叶矩阵在DCT基下的互相关系数。
虽然循环矩阵I的互相关系数比高斯随机矩阵要大,但循环矩阵II和III凭借傅里叶矩阵与变换基之间的极大的非相关性,互相关系数都接近于零。虽然傅里叶矩阵对于离散余弦变换矩阵呈现了相当显著的非相关性,但是傅里叶矩阵对于非时域或频域稀疏的信号重构效果不佳,应用范围有限不及高斯随机矩阵具有普适性。由傅里叶矩阵构造的循环矩阵是一种结构化的随机矩阵,有着傅里叶矩阵强非相关性性能,在实际存储和计算方面也比起高斯随机矩阵更佳。
4.3 单帧重构误差分析
本节对一帧语音信号在不同压缩率不同观测矩阵下,预处理前后的信号重构精度进行研究。定义压缩率为r=M/N,重构精度用均方误差来衡量。对于此帧信号,将DCT域中系数小于0.2的量都置为零,然后对反变换得到的语音信号再进行投影观测。
表3给出的是不同压缩率下三类观测矩阵在DCT域是否进行稀疏预处理的重构误差情况。
根据表3中数据可以得出压缩率越高重构精度越高,在容许的误差范围之内压缩率尽量取到最小来获得最佳的压缩效果。从表3中可以发现误差最小达到0.002 3且不能再小,原因是在DCT域进行稀疏预处理时,已将一部分幅值较小的系数置零,所以得到的新的语音信号较原语音信号本来存在着偏差,但是这一部分产生的误差却比预处理前要小,可见预处理达到了一定的效果。预处理后两类循环矩阵在压缩率为0.4时仍能保证良好的恢复精度,也从仿真角度证明了循环观测矩阵比起高斯随机矩阵的优越性。
4.4 各帧信噪比分析
本节对整段信号进行仿真实验,分析各帧信噪比情况。语音信号用汉明窗分帧,帧长512采样点,帧移为二分之一帧长,采用循环矩阵II进行观测。由于各帧的能量分布不同,对各帧设定动态阈值。定义重构信号第i帧信噪比为:

图3中给出了不同压缩率下各帧信噪比情况。
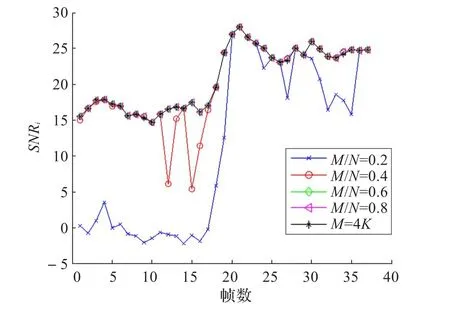
图3 各帧语音信噪比
仿真实验对每帧语音信号根据各帧稀疏系数不同分布,采取了一种简单的自适应观测数选择方法:每帧观测数目取每帧稀疏向量非零个数的四倍。采用自适应观测后每帧信噪比能与压缩率0.6以上的效果相当,但其压缩率到达0.38,平均信噪比达到20.897 9 dB,每帧信噪比与固定每帧压缩率为0.4的情况相比更稳定,没有出现个别语音帧信噪比急剧下降。此外,再使用主观语音质量评估(Perceptual Ealuation of Speech Quality,PESQ)[11]来衡量语音重构质量。PESQ得分在1.0和4.5之间,得分越高说明语音重构质量越好。对重构语音进行PESQ评分得分为3.211,播放重构语音人耳能清晰的听到男声“大衣”的发音。
5 结束语
本文根据语音信号在DCT域的近似稀疏性,将信号接近于零的变换域系数进行置零预处理,得到一个改善了变换域稀疏性的新信号,对其进行观测。针对传统压缩感知中高斯随机矩阵计算存储复杂,提出了使用循环观测矩阵对汉语语音信号进行观测投影。利用最后利用OMP正交匹配追踪方法对观测信号进行恢复,仿真实验表明改进方法不仅对单帧语音还是整段语音信号都能较精确重构,同时能保证比较低的压缩比,对重构语音进行主观评估也能得到不错效果。本文主要思想建立在牺牲小部分信号精确度来换取信号在变换域的稀疏性,通过循环观测矩阵进行观测投影,恢复得到信号精度因此也存在局限。为此,对于汉语语音信号,保证信号精度的前提下寻找稀疏性更好的表示方式,构造性能更佳的观测矩阵,仍是需要继续研究的方面。

表2 各观测矩阵互相关系数
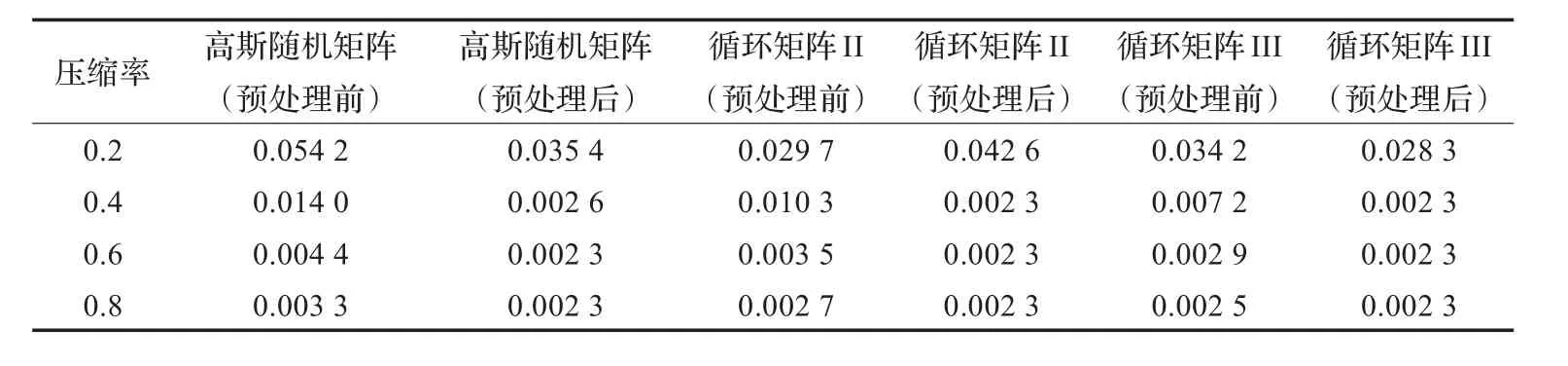
表3 不同压缩率下重构误差比较
[1]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2]Tsaig Y,Donoho D.Extensions of compressed sensing[J]. Signal Processing,2006,86(3):533-548.
[3]Candes E J,Romberg J.Sparsity and incoherence in compressive sampling[J].Inverse Problems,2007,23(3):969-985.
[4]Emmanuel C,Terence T.Near optimal signal recovery from random projections:universal encoding strategies[J]. IEEE Transactions on Information Theory,2006,52(12):5406-5425.
[5]Holger R.Circulant and Toeplitz matrices in compressed sensing[C]//SPARS’09,Saint Malo,2009.
[6]Moreno-Alvarado R G,Martinez-Garcia M.DCT-compressive sampling applied to speech signals[C]//21st International Conference on Electrical Communications and Computers,San Andres Cholula,Puebla,Mexico,2011:55-59.
[7]郭海燕,王天荆.DCT域的语音信号自适应压缩感知[J].仪器仪表学报,2010,31(6):1262-1267.
[8]季云云,杨震.基于自相关观测的语音信号压缩感知[J].信号处理,2011(2):207-214.
[9]Pati Y C,Rezaifar R K.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the 27th Annual Asilomar Conference in Signals,Systems and Computers,Pacific Grove,CA,USA,1993,1:40-44.
[10]Rao K R,Kim D N,Hwang J J.Fast Fourier transform:algorithms and applications[M].Arlington:Springer,2010:34-37.
[11]ITU-T.P.862-2001 Perceptual Evaluation of Speech Quality(PESQ):an objective method for end-to-end speech quality assessment of narrow-band telephone networks and speech codecs[S].2001.
XU Haobo,YU Fengqin
School of Internet of Things Engeneering,Jiangnan University,Wuxi,Jiangsu 214122,China
Based on the compressed sensing theory,it proposes a pre-treatment for the sparsity of transform-domain by zeroing the value below the threshold in the DCT domain.It builds the circulant measurement matrix in three ways instead of Gaussian random matrix,and proves the non-coherence between measurement matrix and DCT base.It uses the OMP method to recover the signal.Simulation experimental result demonstrates that after pre-treatment using circulant measurement matrix has lower restruction error in different compression rate.While analyzing the SNR of each frame,it guarantees a low compress rate and has a good score in PESQ.
speech compressed sensing;Discrete Cosine Transform(DCT)sparse pre-treatment;circulant measurement; Orthogonal Matching Pursuit(OMP)
基于压缩感知原理提出将语音信号DCT域上的小系数在一定阈值下置零预处理来改善变换域稀疏性;用三种方法构造循环观测矩阵作为观测矩阵来代替高斯随机矩阵,并证明了构造的观测矩阵与DCT基之间的非相关性;利用OMP正交匹配追踪方法对观测信号进行恢复。仿真实验结果表明,预处理后使用循环观测在不同压缩率下有更低的重构误差,同时分析各帧信噪比情况保证在比较低的压缩率下仍能得到良好的主观评估。
语音压缩感知;离散余弦变换(DCT)域稀疏预处理;循环观测;正交匹配追踪(OMP)
A
TN912.3
10.3778/j.issn.1002-8331.1304-0329
XU Haobo,YU Fengqin.Speech compressed sensing based on sparse pre-treatment and circulant measurement. Computer Engineering and Applications,2014,50(23):220-224.
国家自然科学基金(No.61075008)。
徐皓波(1988—),男,硕士研究生,主要研究领域:语音信号处理;于凤芹(1962—),女,教授,主要研究领域:语音信号处理、非平稳信号时频分析。E-mail:xhb316@qq.com
2013-04-23
2013-06-13
1002-8331(2014)23-0220-05
CNKI网络优先出版:2013-08-22,http://www.cnki.net/kcms/detail/11.2127.TP.20130822.1408.010.html
