基于多Agent Q学习的RoboCup局部配合策略
2014-08-03赵发君李龙澍
赵发君,李龙澍
安徽大学 计算机科学与技术学院,合肥 230601
基于多Agent Q学习的RoboCup局部配合策略
赵发君,李龙澍
安徽大学 计算机科学与技术学院,合肥 230601
1 引言
RoboCup是近年世界上规模最大的机器人足球大赛,包括仿真和实体两类比赛项目[1]。RoboCup仿真2D是RoboCup最早的项目,也是软件仿真项目的重要组成部分。是各个研究团体在人工智能和多Agent智能体协作方面研究的交流平台[2-4]。
RoboCup仿真2D的比赛平台是模仿人类足球赛的场地和规则制作出来的。整场比赛分为上下半场,各10 min。比赛中以100 ms为周期,每个球员为单独的程序,是由客户端开辟出来的一个独立的线程,仿真球员通过向服务器发送命令来完成自身所要进行的动作[5]。为了使球员在每个周期都能选择最优的动作,现在的很多队伍都采用Q-学习来实现[1,5-8],并且在一定程度上实现了Agent间的协作效果。但是现行的队伍很多采用的方法是:只有带球球员才进行Q-学习获得最优动作[5-8],即在马尔科夫决策环境中(MDP)[3-4,9]选择Q值最大的动作执行,并根据执行动作后的球场评估来更新该动作的Q值,不带球球员则使用事先规定好的策略选择动作,比如,跑位,铲球等[6],这样并不能很好地与带球球员互相协作,更不能对多变的球场状态做出很好的反应。本文采用改进的Q-学习算法使得不带球球员也可以用Q-学习算法得到最优动作来实现多Agent之间的协作,并且约束了算法的使用范围,从而减少了计算量,确保了比赛的实时性。
2 强化学习与Q学习
2.1 强化学习
强化学习[1]是一种无指导的学习,它的主要思想是“与环境交互(Interaction with Environment)”和“试错(trial-and-error)”。这也是自然界中人或动物学习的基本途径。强化学习模型如图1,在学习过程中,Agent不断尝试动作选择,并根据环境的反馈信号调整动作的评价值,最终使得Agent能够获得最大的回报值。

图1 强化学习模型
2.2 Q学习
Q-学习[6]是一种普遍采用的强化学习算法。Q学习的特点是不需要了解环境模型,直接通过学习从动作序列中得到最优的动作,因此Q学习常被用于解决不确定环境下的强化学习问题。
马尔可夫决策过程(Markov Decision Process,MDP)理论在强化学习中有着坚实的理论基础,但是它假定的是Agent所处的环境是固定并且不存在其他自适应Agent的,因此它不满足多Agent环境;Michael L.Littman提出随机对策[2](SG)来作为多Agent强化学习的框架,随机对策是将对策论应用到类MDP环境,是MDP的一般化,也是矩阵对策在多状态下的延伸。
随机对策可定义为五元组 < N,S,{A1,A2,…,An},T,{R1,R2,…,Rn}>,其中,N 为 n 个agent的集合,N= {1,2,…,n},S 是环境的离散状态有限集,Ai为 agenti的动作可选集,T:S×A×S→[0,1]为状态转移模型。T(si,a,si+1)表示从状态 si经过 agent的联合行动 a= {a1,a2,…,an}到达状态 si+1的概率;Ri:S×A×S→R 为agenti的回报函数。在随机对策的框架下,Q值可定义为:

其中,α(0<α<1)为控制收敛的学习率,Vi(st+1)是一个状态值函数:

Q值是通过上述公式的反复迭代而收敛的,上述公式的关键因素是学习策略,即行为a的选择方式和函数Vi(st+1)的定义[3,6]。不同的选择方式会产生不同的多Agent学习算法[1]。
3 Agent球员执行策略
传统的球员执行策略是根据决策树来进行动作选择的[9-10],决策树的执行过程如图2。
其中,只有当Agent控球时,才使用球场评估函数运算得到该Agent下周期的动作[6],如图3。

图2 agent球员执行的决策树

图3 带球球员动作执行框架
而当Agent不控球时,则根据阵型文件或者一定策略来执行相应的动作,因此这个方法严格来说属于单Agent的学习算法,球队的协作很少,进攻防守方式单一。下面一章将重点介绍改进的多Agent Q学习。
4 改进的配合策略
4.1 状态-动作对的确定
球场上情况复杂,需要考虑的因素太多。但是要达到局部的配合,首先要知道自己所处的位置SA和球的位置SB,这样才能确定球员本身是否出在配合的范围内;其次是否自己控球LA还有是否是我方控球LB,用来确定配合的策略是防守还是进攻。于是将<SA,SB,LA,LB>作为球场上局部范围内环境状态的描述。
为了减少因为SA,SB连续的坐标信息而增加的环境状态的数量,对球场上的位置进行了离散。本文中的位置都是在这个离散方式的基础上讨论的。具体的离散方法如下:将球场划分为60×10个小的区域,其中 X轴方向分为60等份,Y轴方向分为10等份,这样就可以用一对离散化的(i,j)来描述球场上的位置信息。LA,LB的取值为0或1,0表示不控球,1表示控球,当球处于自由状态时(即任何一方都不控球),LA,LB取0。
因 此 环 境 的 状 态 信 息 描 述 为 <SA,SB,LA,LB>=<(iA,jA),(iB,jB),{0,1},{0,1}> (0 ≤ i≤ 59,0 ≤ j≤ 9)。
根据状态信息来确定相应动作集:当Agent为控球球员,动作集为上述决策树中控球时的动作,即{shoot,pass,cross,dribble,selfpass};当 Agent不控球时,但是控球方为我方时,动作集为{gotopoint,turntoball};当Agent不控球时且对方控球时,动作集为{gotopoint,turntoball,tackle}。
4.2 reward值的确定
本文中的reward值的确定比较复杂,分为:Agent控球,Agent不控球但我方有控球权,对方控球三种情况,下面将分别讨论这三种情况下的reward值的确定。
4.2.1 Agent控球
(1)我方进球,r=1;
(2)球到达射门点,r=0.9;
(3)球出界,r=0;
(4)变为对方控球,r=-0.9;
(5)对方进球,r=-1;
(6)否则,r=区域基础回报+区域内部回报+f(x)。
上述的射门点是球队根据球队特点和禁区内的各种复杂情况事先计算出来的位置,在这些位置射门时进球的概率很高,因此到达这些点时回报值应仅次于进球时的回报值。
在情况(6)中,继续沿用以前的章惠龙等提出的算法[10],但是区域的划分不同,划分的具体情形如图4。

图4 球场划分策略
如图4,将球场划分为关于 X轴对称的9个区域,将这9个区分的基础回报分别设定为-0.4,-0.6,-0.5,-0.3,-0.3,0.3,0.3,0.5,0.7 。
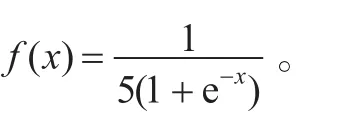
上面两个参数的设定不仅保证了区域之间的差异性,也保证了区域值得连续性,使得两个区域的交界处的回报值差距不至于太大。
区域内部回报是由球员之间的位置关系确定的,在球队中事先用一个函数确定在这个范围中的最适合配合球员P1和最危险的对方球员P2,因此区域内部回报:
当 d1>5.0,区域内部回报 =(XA+(d1-5.0)×2.0× XA-d3)/100;
当 3.0<d1≤5.0,区域内部回报 =(XA+(d1-d2)×2)/ 100;
当d1≤3.0,区域内部回报 =(XA-d3)/100-本区域基础回报。
公式中 XA为球的 X坐标,d1为P2与球之间的距离,d2为P1与球之间的距离,d3为球与对方球门之间的距离。公式中通过控制XA的倍数来控制带球速度;通过控制d3的大小来控制是否将球推向对方球门;通过控制d1的大小来在一定程度上控制是否摆脱P2;这里P1、P2是根据球员是否适合铲球,有没有球员盯住等许多复杂因素确定的,而不是单纯地使用最近的球员,确定方法不是本文重点,这里将不再讨论。
4.2.2 Agent不控球但我方有控球权
(1)如果自身是最佳配合球员,r=区域基础回报+ f(x)+(XB+d4-d5)/100。
(2)如果自身不是最佳配合球员,r=(XB+d4)/100。
其中区域基础回报和 f(x)就是前面讨论过的值,d4为自身与球之间的距离,d5为经过一定方法得到的对自己最有威胁的对方球员(一般情况下为离自己最近的对方球员,除非此队员有人盯防)与自己的距离,通过控制XB的倍数来控制跑动速度。这样确定的目的是因为,如果自身为最佳配合球员,控球球员可能将球传给自己,因此要跑向球,并且要保证周围没有对方球员盯防,如果自身不是最佳配合球员,则跑向对方球员进行阻挡对方跑位,此外,由于情况(1)加入了区域基础回报,则会考虑到区域之间的差异,尽量向对方球门方向带球。
4.2.3 对方控球
(1)如果得到球,r=1.0;
(2)如果自己是离球最近的球员,r=(XC-d6)/100;
(3)否则,r=(XC+d7×2+d6-d8)/100。
其中,d6为与球的距离,d7为自身与最近对方球员P3的距离,d8为 P3与球的距离,XC与目标的距离有关,用来控制球员的跑动速度。由此可见,当对方控球时,己方球员首先是争取获得控球权,如果不能取得控球权,则先主动上前去拦截,否则盯防距离自己最近的进攻球员,挡在球与该球员P3之间,防止控球球员传球。
4.3 更新状态-动作表中的Q值
本文实验的Q值是按照下面公式进行更新的:
Qt+1(s,a)=(1- α)Qt(s,a)+ α[rt+ βV(st+1)] (3)
其中,当在训练的时候α=0.35,当Q值趋于稳定的时候 α=0.1,β=0.8,

每个周期Agent都会从状态-动作表中找到对应状态中Q值最大的动作执行,执行过后再根据上述公式更新对应的Q值。更新时都会找到a中的所有动作,这时就要选择一个范围d,在这个范围内的所有球员都将考虑进去,用来更新Q值,根据球的最大速度和衰减率得出d=30。
5 实验及结果
将上述算法植入到校队代码中并在RoboCup仿真2D的平台上进行实验。通过大量的反复学习,使得Q值收敛于一个稳定的值,以进球和配合数作为统计数据,通过实验发现,配合数和进球数较采用传统Q学习的方法有明显上升。
如图5(a)所示,改进的多Agent方法进攻能力有所提升,图5(b)所示,改进的多Agent Q学习的配合数明显增多,另外还可以发现传统的多Agent Q学习的配合数一直不稳定,这说明传统多Agent Q学习不存在配合,即使有配合也只是偶然出现的巧合,因为它设计时没有考虑到Agent配合的情形。当Q值趋于稳定时,再进行200次防守实验,实验结果如表1。

图5 进球数和配合数的统计数据

表1 平均被进球数统计结果
从表1可以看出,多Agent Q学习的代码相对于传统多Agent Q学习代码,防守实力都大大增强,与实验的初始设计目标相符。
6 结束语
本文主要是将多Agent的Q学习应用到了RoboCup仿真2D中,使得球队在比赛中配合更多,进而使球队的进攻和防守能力得到一定的增强。实验结果表明,学习效果有明显的提高。因此,采用此方法解决RoboCup中的配合问题行之有效。采用此方法受到计算空间和时间的限制,只能采用局部配合才能保证比赛的实时性。
[1]Celiberto L A,Ribeiro C H C.Heuristic reinforcement learning applied to RoboCup simulation agents[C]// LNCS 5001,2008:220-227.
[2]Mota L,Lau N,Reis L P.Co-ordination in RoboCup’s 2D simulation league:setplaysasflexible,multi-robot plans[C]//RAM,2010:362-367.
[3]Bai Aijun,Wu Feng,Chen Xiaoping.Online planning for large MDPs with MAXQ decomposition[C]//Proceedings ofthe 11th InternationalConference on Autonomous Agents and Multiagent Systems,2012:1215-1216.
[4]Zhang Zhongzhang,Chen Xiaoping.A factored hybrid heuristic online planning algorithm for large POMDPs[C]// Proceedings of the 28th Conference on Uncertainty in Artificial Intelligence,2012:934-943.
[5]向中凡.Q学习角色值法在机器人足球比赛中的应用[J].电子科技大学学报,2007,36(4):809-812.
[6]孟祥萍,王欣欣,王圣镔.多Agent Q学习几点问题的研究及改进[J].计算机工程与设计,2009,30(9):2274-2276.
[7]刘亮,李龙澍.基于局部合作的RoboCup多智能体Q-学习[J].计算机工程,2009,35(9):11-16.
[8]柯文德,彭志平,蔡则苏,等.基于π演算的足球机器人协作Q学习方法[J].计算机应用,2011,31(3):654-656.
[9]Kalyanakrishnan S,Liu Y,Stone P.Half field offense in RoboCup soccer:a multiagentreinforcementlearning case study[J].Computer Science,2007,4434:72-85.
[10]章惠龙,李龙澍.Q学习在RoboCup前场进攻动作决策中的应用[J].计算机工程与应用,2013,49(7):240-242.
[11]顾晓锋,张代远.机器人足球比赛接球策略设计[J].计算机应用,2005,25(8):1858-1859.
[12]李实,陈江.清华机器人足球的结构设计与实现[J].清华大学学报,2001,41(7):94-97.
[13]张波,蔡庆生,陈小平,等.基于智能体团队的RoboCup仿真球队[C]//第三届全球智能控制与自动化大会论文集,2000.
[14]杨煜普,李晓萌,许晓鸣.多智能协作技术综述[J].信息与控制,2001,30(4):337-342.
[15]李实,徐旭明.国际机器人足球比赛及其相关技术[J].机器人,2000,22(5).
ZHAO Fajun,LI Longshu
School of Computer Science and Engineering,Anhui University,Hefei 230601,China
Because many multi-Agent cooperative problems can hardly be solved in RoboCup,this paper investigates a regional cooperative multi-Agent Q-learning method.Through subdividing the stadium area and rewards of agents,the agents’collaboration ability can be strengthened.As a result,the team’s offensive and defensive abilities are enhanced. At the same time,the agents can spend less time learning via restricting the using range of the algorithm.Consequently, the real-time of the game can be ensured.Finally,the experiment on the platform of the simulation 2D proves that the effect of this method is much better than that of the previous one,and it fully complies with the design of the original goal. Key words:stochastic game;Q-learning;real-time;regional cooperation;RoboCup simulation 2D;cooperative strategy
针对RoboCup(Robot World Cup)中,多Agent之间的配合策略问题,采用了一种局部合作的多Agent Q-学习方法:通过细分球场区域和Agent回报值的方法,加强了Agent之间的协作能力,从而增强了队伍的进攻和防守能力。同时通过约束此算法的使用范围,减少了学习所用的时间,确保了比赛的实时性。最后在仿真2D平台上进行的实验证明,该方法比以前的效果更好,完全符合初期的设计目标。
随机对策;Q-学习;实时性;局部合作;RoboCup仿真2D;配合策略
A
TP181
10.3778/j.issn.1002-8331.1301-0093
ZHAO Fajun,LI Longshu.RoboCup regional cooperative strategy based on multi-Agent Q-learning.Computer Engineering and Applications,2014,50(23):127-130.
安徽省自然科学基金(No.090412054);安徽高等学校省级自然科学基金(No.KJ2011Z020)。
赵发君(1988—),男,硕士研究生,主要研究方向为仿真机器人足球研究;李龙澍,教授,博士生导师,主要研究方向为软件设计技术、智能信息处理和Agent应用技术等。E-mail:zhaofajun216@126.com
2013-01-10
2013-02-22
1002-8331(2014)23-0127-04
CNKI网络优先出版:2013-04-08,http://www.cnki.net/kcms/detail/11.2127.TP.20130408.1648.013.html
