基于多目标粒子群的非线性系统PID控制器设计
2014-08-03伍思敏
伍思敏,陈 珺,刘 飞
江南大学 自动化研究所 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
基于多目标粒子群的非线性系统PID控制器设计
伍思敏,陈 珺,刘 飞
江南大学 自动化研究所 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
1 引言
PID控制器自产生以来,由于结构简单、鲁棒性强等优点,一直是工业生产过程中应用最广泛、最成熟的控制器。在实际的工程控制中,由于控制对象越来越复杂,对控制品质的要求越来越高,被控系统不仅普遍存在着非线性、时变性等不确定因素,往往还要同时综合考虑系统的准确性、稳定性、快速性等多个性能指标[1]。为了克服这一问题,近年来一些学者利用控制量与偏差信号之间的非线性关系设计出非线性PID控制器[1]以达到改善控制性能的目的。这类方法的优点是非线性构造能力强,能够逼近任意的非线性系统,但是参数调试较为复杂,不利于工程应用[2]。随着模糊控制、神经网络等智能控制理论和遗传算法、粒子群算法等优化算法理论的发展,形成了传统PID控制与智能控制相结合的智能PID控制策略。
粒子群优化算法(Particle Swarm Optimization,PSO)是由Kennedy和Eberhart于1995年提出的一种新的基于群智能的优化算法,已被证明能够有效地解决非线性、可微的、多目标优化等问题。文献[3]中作者将粒子群算法成功地应用于非线性有理滤波模型,在文献[4]中,作者将PSO用于自动电压调节器(AVR)的PID控制器优化设计。文献[5]将基于非支配策略的遗传算法П用于多目标湿稳定剂PID控制器整定中,粒子群算法由于参数设置少,且没有遗传算法的交叉变异操作,在解决多目标优化问题上非常有竞争力。
许多学者提出了多目标粒子群优化算法[6-7],近年来:文献[8]采用基于支配关系及适应度共享的策略保持解集的分布性,文献[9]提出了一种多种群的粒子群算法,每个子种群与每一个子问题联系起来;文献[10]提出一种ε占优的自适应多目标粒子群算法(εDMOPSO),针对算法易收敛到伪Pareto前沿和收敛速度慢的问题,利用ε占优更新非劣解等策略改善了算法。
本文考虑一种基于非劣最优排序的多目标粒子群算法,解决了针对一类非线性系统的PID控制器设计问题。
2 多目标粒子群优化算法
基本的粒子群算法更新公式如下:

其中 d=1,2,…,D 是目标搜索空间的维数,i=1,2,…,N是粒子个数,是粒子i在第t次迭代中第d维的速度,x是粒子i在第t次迭代中第d维的位置,是粒子i在第t次迭代中第d维的个体最优位置,g是粒子i在第t次迭代中第d维的全局最优位置,r1和r2为均匀分布于[0,1]之间的随机数,c1和c2为加速因子(acceleration constants),用来调节每次迭代的步长,ω为惯性因子(inertia weight)。
多目标优化问题通常由两个或者两个以上的目标组成,目标之间往往是相互制约的关系。多目标优化问题一般不存在惟一的全局最优值,但是可以存在这样的解:对一个或几个目标函数不可能进一步优化,对其他目标函数不至于劣化,这样的解组成了一个非劣最优解集(Pareto解集),通过优化算法希望求得足够多的解均匀分布在Pareto前沿上,然后寻求Pareto解集中的一个或多个满意解[11]。Pareto最优的概念如文献[12]所述。
本文基于Pareto快速非劣排序的多目标粒子群算法[13]和基于拥挤距离排序的算法[14],针对非线性系统粒子易陷入局部最优的情况,在粒子进行局部最优值更新时,若粒子的历史最优位置连续M代没有得到提升,很可能是粒子过早地收敛到了局部最优值,为了让粒子跳出局部最值,此时给粒子重新赋值,再进一步寻优,M可以根据经验取值。同时在算法后期对最优解集进行筛选,这样做的目的是去掉等级低的和受其他粒子支配的粒子,保留最优的外部解集,在实际应用中可以不用再进行筛选。改进后的算法搜索能力得到提升,算法外部解集分布均匀。
3 基于多目标粒子群的针对一类非线性系统的PID控制器设计
标准PID控制器的数学模型为:

其中,e(t)表示系统误差,u(t)表示控制器输出,Kp、Ki、Kd分别表示PID控制器的比例、积分和微分增益。
本文基于改进的多目标粒子群算法,设计了针对一类倒立摆非线性系统的PID控制器,使得控制系统的输出响应满足给定的控制性能要求。在改进的多目标粒子群算法中,Kp,Ki,Kd定义为算法的三个决策变量,即xi=(Kp,Ki,Kd)。考虑的一类非线性系统描述如下:

其中 f和g是非线性函数,u是控制器的控制作用,结合标准PID控制器数学模型构造,y是非线性系统的实际输出。设计的控制系统结构框图如图1所示,其中R是系统的给定输入。
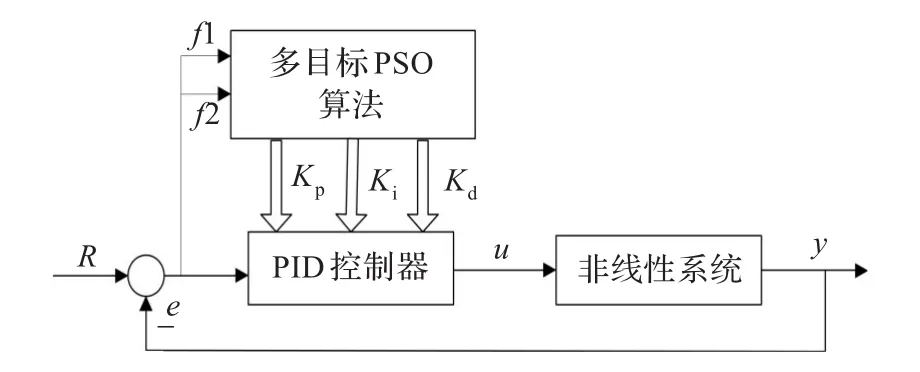
图1 基于多目标粒子群算法的PID控制器系统框图
多目标粒子群算法是根据非线性系统输出的若干性能指标来进行迭代寻优的,性能指标是设计控制器时希望被控非线性系统满足的控制性能,通过系统的实际输出获得,选取不同的性能指标决定了算法寻优的方向。因此性能指标应该被恰当地定义,才能使优化达到满意的效果。本文定义PID控制的超调量和调节时间为需要同时满足的两个优化指标,即在满足超调量最小的同时,使得调节时间也最短,分别用 f1和 f2表示,f1代表控制系统的调节时间tc,f2代表控制系统的超调量σ,那么多目标粒子群算法的两个目标是最小化 f1和f2。其中,调节时间tc是通过判断误差在[-0.05 0.05]范围之间的数值,并且留下这些数值的序号,那么序号里最后一个序号所对应的时间就是调节时间,判断输出最大时误差的绝对值就是超调σ,这是因为误差是指给定减去输出,输出最大时对应的误差最小(误差为负),此时的误差取绝对值,就是超调σ了。
该控制系统输出满足精确跟踪给定值的同时,同时满足超调量小、调节时间短的性能指标,得到一组控制器优化权值。那么设计基于改进多目标粒子群算法的,针对一类非线性系统的PID控制器的完整步骤如下:
(1)根据公式(3)调整被控非线性系统的形式,搭建PID非线性控制系统,并初始化系统运行时间T和其他参数;初始化多目标粒子群算法种群的大小N,最大迭代次数Gmax和粒子速度、位置范围,以及加速因子c1、c2,惯性权值ω和最大停滞代数M 。
(2)基于改进的多目标粒子群算法,依据最小化两个性能指标的目标,搜寻针对一类非线性系统的PID控制的一组最优增益 Kp、Ki、Kd,步骤如下:
步骤1根据给定范围随机初始化一组粒子值。
步骤2根据适应度函数评价每个粒子适应值,对粒子进行基于非劣最优和密度距离的快速排序。
步骤3根据锦标赛选择策略选取个体的局部最优值和全局最优值,第一次迭代时,直接将粒子值定义为局部最优值。
步骤4判断粒子是否除最高级外连续M代(根据经验,M可以取7)未提升顺序,若是则给该粒子重新赋值。
步骤5根据公式(1)、(2)更新每个粒子的速度和位置。
步骤6如果满足迭代条件(达到了迭代最大值),则算法结束,基于非劣最优和密度距离排序筛选出最优非劣解集,同时依据密度距离调整最优非劣集的个体,使Pareto前沿分布均匀分散,若未满足迭代条件,则返回步骤2。
(3)控制器最终会得到一组最优解集,决策者选择最优解集中的最优解进行PID控制。
由于多目标粒子群算法是基于迭代寻优的算法,因此将算法作为控制器的主体编写m文件,PID控制非线性系统为算法的子文件被调用。
4 倒立摆系统跟踪控制仿真
倒立摆系统是有一定复杂性的非线性系统,也是一类典型的非线性被控对象。本文考虑的一个非线性倒立摆系统的动态微分方程描述如下[15]:其中 y=x1是基于倒立轴的摆角的弧度,x2是摆点的角速度,g=9.8 m/s2是重力加速度,mc=1是小车的质量,m=0.1 kg是摆的质量,l=0.5 m是摆一半的长度,u是被控对象的控制输入,这里是PID控制的输出。
本文用matlab的m文件编程实现多目标粒子群算法,通过SIMULINK搭建PID控制系统,算法通过sim函数调用workspace里个体的适应度值进行仿真。仿真非线性系统的采样时间设置为0.01,针对该非线性系统,改进的多目标粒子群算法的其余参数设置详见表1。控制的目的是使得倒立摆的摆角的输出y跟踪给定输入 R=1(阶跃输入),初始值为 (x1(0),x2(0))=(0.1,0)。

表1 基于多目标粒子群的倒立摆系统PID控制器设计参数
为了验证改进的多目标粒子群算法的有效性,考虑以下仿真策略:
(1)在得到多目标优化最优解集中,随机挑选其中四个非劣最优解,进行针对式(4)的倒立摆非线性系统PID跟踪控制仿真,运行控制器得到的非劣最优解集见图2,仿真结果如图3。从图3中可以看出PID控制精确有效地跟踪给定值,超调量很小,不到2%,调节时间短,在1 s左右可以基本跟踪给定值。该策略验证了求得的最优解集中解的可行性高,效果好。

图2 多目标粒子群算法优化非线性系统PID控制参数的Pareto前沿
(2)为与同类方法比较,基于粒子群算法,同理设计PID控制器,针对式(4)的非线性控制系统仿真,得到一个PID控制增益,同样进行倒立摆角度的跟踪控制,仿真结果如图4虚线所示,与本文随机选取的一个控制效果对比,如图4实线所示。从图中可以看出本文给出的基于多目标粒子群的PID控制器控制结果超调量更小,调节时间更短,比基于粒子群的PID控制器有明显优势。
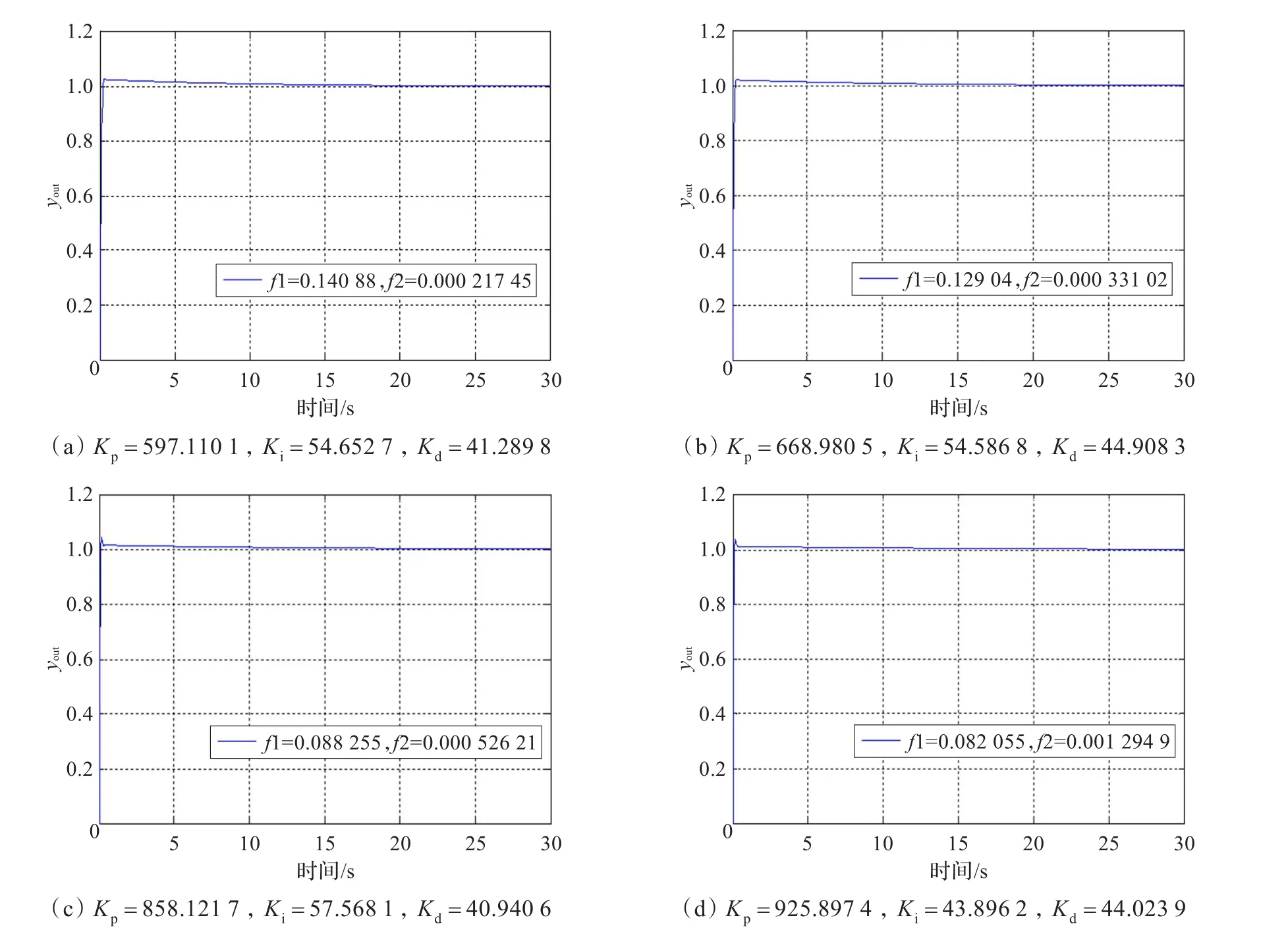
图3 优化得到的PID控制参数跟踪阶跃信号控制倒立摆角度

图4 控制效果对比图
(3)为了验证该控制器在满足精确跟踪给定的前提下,具有一定抗干扰能力,给系统设定一个大小为0.2的干扰,在PID控制系统运行20 s时加入。
从图2的最优解集中随机选取一个控制参数,进行针对式(4)的倒立摆非线性系统PID跟踪控制仿真,仿真结果如图5。从图中可以看出,在20 s时加入干扰,控制器输出能够在较短的时间内恢复到给定跟踪值,说明该控制器抗干扰性能好。

图5 加入干扰后的控制效果
5 结论
本文基于改进的多目标粒子群算法,给出了一个针对一类非线性系统的PID控制器设计方法。改进的基于Pareto最优排序的多目标粒子群算法能更好地跳出局部最优。将PID控制器的两个性能指标作为多目标粒子群算法的目标函数,稳定有效地求出一组最优控制增益。采用经典的非线性倒立摆系统作为PID控制被控对象进行仿真,控制效果稳定、快速、准确,并与基于粒子群算法的PID控制器的控制效果对比,调节时间更短,超调量更小,有明显优势。该控制器抗干扰能力强,并且可以得到一组优化参数,实际应用选择余地更大。该控制器还可以根据实际控制需要,灵活选择控制目标,达到更好的控制效果。
[1]孙轶民,郭雷.一种新型非线性PID控制器及其参数设计[J].控制理论与应用,2009,26(4):439-442.
[2]周颖,张磊,裘之亮,等.基于自适应遗传算法的非线性PID控制器[J].河北工业大学学报,2010,39(1):47-55.
[3]Lin Y L,Chang W D,Hsieh J G.A particle swarm optimization approach to nonlinear rational filter modeling[J]. Expert System with Applications,2008,34(1):1194-1199.
[4]Gaing Z L.A particle swarm optimization approach for optimum design of PID controller in AVR system[J]. IEEE Transactions on Energy Conversion,2004,19(2):384-391.
[5]Panda S.Multi-objective PID controller tunning for a FACTS-based damping stabilizerusing non-dominated sorting genetic algorithm-П[J].International Journal of Electrical Power and Energy Systems,2011,33(7):1296-1308.
[6]Deb K,Pratap A,Agarwal S,et alA fast and elitist multiobjective Genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[7]Tavakkoli-Moghaddam R,AzarkishM,Sadeghnejad-Barkousaraie A,et al.A new hybrid multi-objective Pareto archive PSO algorithm for a bi-objective job shop scheduling problem[J].Expert Systems with Application,2011,38(9):10812-10821.
[8]Janson S,Middendorf M.A hierarchical particle swarm optimizer and its adaptive variant[J].IEEE Systems,Man and Cybernetics-Part B,2005,3(6):1272-1282.
[9]Zhang Yong,Gong Dunwei,Ding Honghai.Handing multiobjective optimization problem with a multi-swarm cooperative particleswarm optimizer[J].Expert System with Application,2011,38:13933-13941.
[10]刘衍民,赵庆祯,牛奔,等.基于ε占优的自适应多目标粒子群算法[J].控制与决策,2011,26(1):89-95.
[11]徐鸣,沈希.一种多目标粒子群改进算法的研究[J].控制与决策,2009,24(11):1713-1728.
[12]Deb K,Pratap A,Agarwal S.A fast and elitist multiobjective genetic algorithm:NSGA-П[J].IEEE Transactions on Evolutionary Computation,2000,18(2):125-147.
[13]裴胜玉,周永权.基于Pareto最优解集的多目标粒子群优化算法[J].计算机工程与科学,2010,32(11):85-88.
[14]李中凯,谭建荣.基于拥挤距离排序的多目标粒子群优化算法及其应用[J].计算机集成制造系统,2008,14(7):1329-1336.
[15]Chang Weider,Shin Shunpeng.PID controller design of nonlinear systems using an improved particle swarm optimization approach[J].Communication in Nonlinear Scienceand NumericalSimulation,2010,15(11):3632-3639.
WU Simin,CHEN Jun,LIU Fei
Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education),Institute of Automation,Jiangnan University,Wuxi,Jiangsu 214122,China
Since production,the PID controller has been widely used in industrial production processes,with easy implementation and mature theoretical analysis.Along with the increasingly high demand for quality,this paper considers the accuracy,stability and rapid of the multiple system performance indicators at the same time and presents a PID optimization control system design for a class of nonlinear systems based on the Pareto optimal sequencing multi-objective particle swarm optimization.For simulation,a classic nonlinear inverted pendulum system is illustrated as objects of PID control. The overshoot and adjustment time are defined as the fitness functions of the multi-objective particle swarm optimization. The typical nonlinear inverted pendulum tracking control uses a set of Pareto optimal control parameters and the result testifies that the tracking control is accuracy and stability.
multi-objective Particle Swarm Optimization(PSO);Proportion-Integration-Differentiation(PID)control; nonlinear system;inverted pendulum control
PID控制器自产生以来,一直是工业生产过程中应用最广泛、最成熟的控制器。随着控制品质的要求越来越高,综合考虑系统的准确性、稳定性、快速性等多个性能指标,基于改进的Pareto最优排序多目标粒子群算法,给出一个适用于一类非线性系统的PID控制器设计方法。采用经典的非线性倒立摆系统作为PID被控对象进行仿真,将超调量和调节时间两个目标作为多目标粒子群算法的目标,求出一组Pareto最优控制参数,通过跟踪控制得到精确稳定的控制效果。
多目标粒子群算法;比例-积分-微分(PID)控制;非线性系统;倒立摆控制
A
TP273
10.3778/j.issn.1002-8331.1211-0165
WU Simin,CHEN Jun,LIU Fei.PID control of nonlinear systems based on multi-objective particle swarm optimization.Computer Engineering and Applications,2014,50(23):69-72.
国家自然科学基金(No.NSFC61134007);江苏省基础研究计划(自然科学基金)(No.BK2012111);中央高校基本科研业务费专项资金资助(No.JUSRP111A40);江苏高等学校优秀科技创新团队;江苏高校优势学科建设工程资助项目。
伍思敏(1987—),女,硕士研究生,研究方向为控制理论与控制工程。E-mail:wusimin1987@163.com
2012-11-14
2013-01-18
1002-8331(2014)23-0069-04
CNKI网络优先出版:2013-02-07,http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1420.018.html
