基于最优组合赋权的可变模糊模型在水质评价中的应用

鞠学亮，张 戈，2，高 跃，田 冲

(1.辽宁师范大学城市与环境学院，辽宁大连 116029;2.辽宁师范大学自然地理与空间信息科学辽宁省重点实验室，辽宁大连 116029)

随着水资源问题的日益突出，水质评价成为水环境保护和治理的一项基础性工作。为防止水质进一步恶化，加强水资源科学管理，对水质做出客观、合理的评价显得尤为重要［1-2］。目前水质评价的主要方法为B-P人工神经网络法、灰色关联分析法、单因子评价法、模糊综合评价法等。其中BP人工神经网络法对于神经元的权重和阈值的确定具有经验性，且计算复杂，需要编程来实现。灰色关联分析法通过关联度的概念衡量各因素之间关联程度，具有较好的可比性，但结果的均值化问题有待解决。单因子评价法只考虑超标严重的指标对水质的影响，弱化了其他指标的作用［3-7］。

由于水体本身具有流动性、多变性和复杂性，在进行水质综合评价时，评价标准的标准量化、指标和权重选取的模糊性，都会影响最终水质评价结果。可变模糊评价在模糊集合理论基础上将评价准则细分为吸引域和范围域，将事物渐变过程中的不分明性用数学形式进行表达，使得模糊数学中的可变模糊综合评价法成为处理这种外延边界“模糊不清”问题的较好方法［8-10］。在进行多指标评价过程中，各指标权重的确定是否合理，直接影响到决策结果的可靠性和有效性。目前，权重的确定大体可分为主观权重和客观权重。确定主观权重的主要方法有:层次分析法、有序二元对比法、专家调查法等，主观权重根据决策者的经验进行评价，主观因素影响明显，随意性较大。确定客观权重的主要方法有:熵值法、主成分分析法、改进AHP法、多目标规划法等。客观权重根据数据指标本身的特点进行分析，从而确定权重，特点是客观性较强［11-12］。

针对可变模糊评价中权重的选取具有一定的经验性问题，本文通过有序二元对比法确定主观权重，通过熵值法确定客观权重，结合基于离差平方和的最优组合模型进行优化组合［13］，确定最终权重，然后结合可变模糊集理论建立地表水水质评价数学模型。

1 基于最优组合赋权的可变模糊模型

1.1 可变模糊评价模型

依据可变模糊集理论［14］，建立水质综合评价模型，步骤如下:

步骤1 对地表水水质资料进行预处理，选取具有代表性的m个评价指标，得到样本资料的矩阵特征值。根据评判集样本选取c个级别进行评判，并规定1级最优，c级最差，分别确定可变模糊集合的吸引域Iab、范围域Icd和M值。

式中:X为样本标准值矩阵;a、b为指标i级别h吸引域区间的上、下限;c、d为指标i级别h范围域区间的上、下限;M为吸引域中相对差隶属度等于1的点值矩阵。

步骤2 确定样本对各级别指标的相对隶属度矩阵，将待评价指标xij与Mih值进行比较，选用相对隶属度计算公式求出xij对于各级别的相对隶属度，若xij位于Mih点的右侧，其相对隶属度模型为

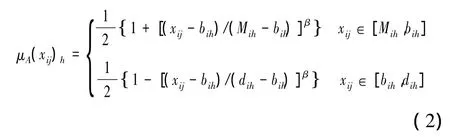
若xij位于Mih点的左侧，其相对隶属度模型为

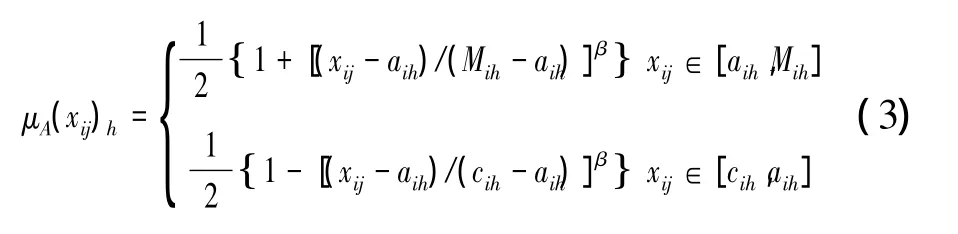
式中:μA(xij)h为评价指标xij对h级的相对隶属。

分别计算样本对h级别的相对隶属度矩阵:

步骤3 运用模糊可变识别模型计算样本对级别的综合相对隶属度:

式中:a为优化准则参数;p为距离参数;u'hj为非归一化的综合相对隶属度;wi为指标权重。

根据参数的4种组合得到相应的归一化综合隶属度矩阵:

应用级别特征值公式

由此可得到该地区地表水水质评价结果。

1.2 基于最优组合赋权法确定权重

1.2.1 主观权重

二元对比分析法在系统分解和综合的基础上，利用人的知识和经验对一系列系统单元非结构性的模糊优选问题进行求解［14］。将各指标进行定性排序，并求出满足一致性条件下的定性排序的二元比较矩阵g=(gij)(gij为指标i对j的重要性模糊标度)，并结合模糊概念语气因子和定量标度关系(表1)查得相应的相对隶属度［8］。根据矩阵g，构造矩阵β:

通过式(8)确定归一化的权重:

表1 语气算子与定量标度、相对隶属度关系

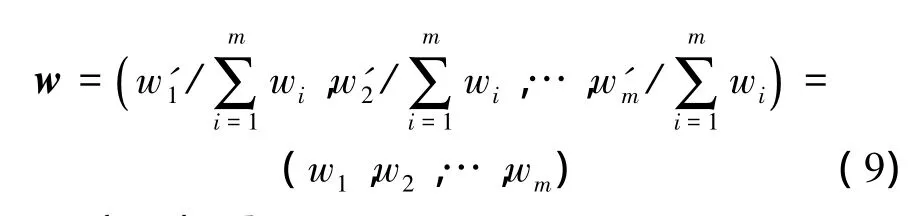
1.2.2 客观权重

熵值法通过各项监测指标的差异度确定各指标的权重［15］，主要步骤有以下2个:

步骤1 对原始数据矩阵进行标准化。设有m个指标，通过对n个评价对象规范化处理，确定各个指标的属性值为rij，其中rij为第j个评价对象在第i个指标上的标准值，rij∈［0，1］。

步骤2 定义熵及熵权。定义第i个指标的熵为

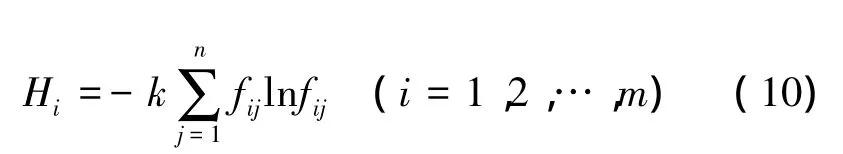
当fij=0时，令fijlnfij=0。

某个指标的信息价值取决于指标的信息熵和1的差值，于是根据式(10)确定的熵值，可计算得第i个指标的权重为

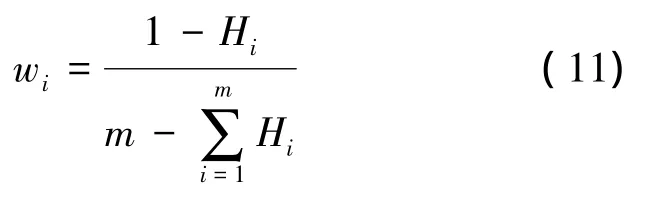
1.2.3 最优组合模型确定权重

假设在多属性决策问题中有n个样本，m个评价指标。最优组合赋权法是在多个决策者组成的群决策方案下，将几种单一模型的权重进行协调取优的一种方法［16］。结合主客观权重的特点，通过求解数学规划模型，确定主客观权重在多属性决策问题中各自的比重，使得最终确定的权重能够同时反映主观性和客观性。设最优组合权系数向量:w=(w1，w2，…，wm)T，令:

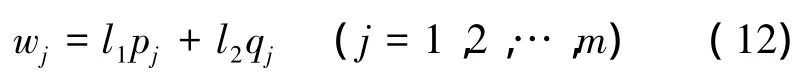
式中:wj为第j个指标的权重;l1，l2为组合权系数向量的线性系数，且满足约束条件l1≥0，l2≥0,1;pj和qj分别为第i个指标的主观权重和客观权重。

从式(12)可看出，线性系数的改变会影响最优组合权系数，因而最优组合赋权法的关键问题是确定l1，l2。根据简单线性加权法，可建立有关wj的多目标综合评价值。

式中:Qi为第i个样本m个评价指标的综合评价值之和;bij为第i个样本第j个指标原始数据规范化后的数值。

一般来说Qi越大表示评价越优，但在多属性决策中，如果权系数选取不当，会导致各决策方案属性评价值之间差别很小，不利于决策方案的排序，所以确定的赋权系数应适当使各方案的离散程度最大。故只需在约束条件下使离差平方和最大［17］。

故等价于求解以下优化问题:

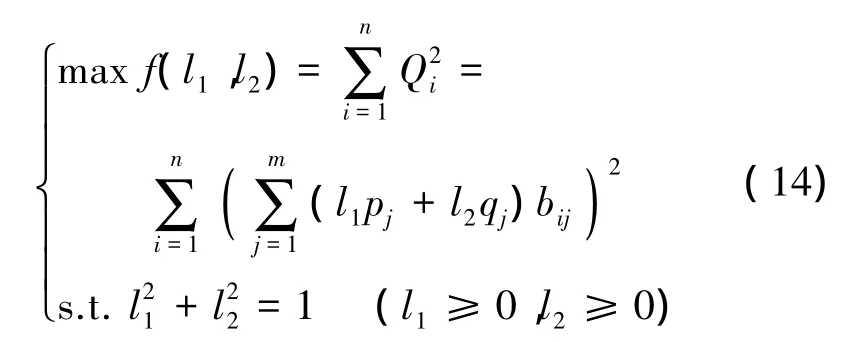
用Matlab软件求解该优化模型，将求得的最优解l*1，l*2进行归一化处理，得到l1，l2。由此，可得每个评价指标的权重:

进行归一化处理得到最终权重。

2 实证应用——以鞍山市城区地表水水质评价为例

2.1 研究区域概况

鞍山市城区位于辽宁省鞍山市中部地区，西靠海城市，东临辽阳市太子河区，北部为辽阳市辽阳县，鞍山市城区总面积为624km2。鞍山市气候类型为暖温带半湿润季风性大陆气候，其特点是雨热同步，降水充沛。鞍山市市区多年平均降雨量为704.3mm，其补给来源主要为大气降水。

2.2 评价因子和评价集

本文选取2010年鞍山市城区南沙河、运粮河和杨柳河上6个监测断面的监测数据。为反映该地区当年水质整体水平，取该年的4月(枯水期)、8月(丰水期)和10月(平水期)的平均值进行水质评价。该地区地表水主要污染物来自城区的生活污水和工业废水，根据数据资料分析选取具有代表性的污染评价因子，分别为 COD、BOD5、NH3-N、TP、DO和石油类(表2)。根据GB3838—2002《地表水环境质量标准》将水质分成5个等级(表3)，采用最优化赋权可变模糊模型进行水质评价。

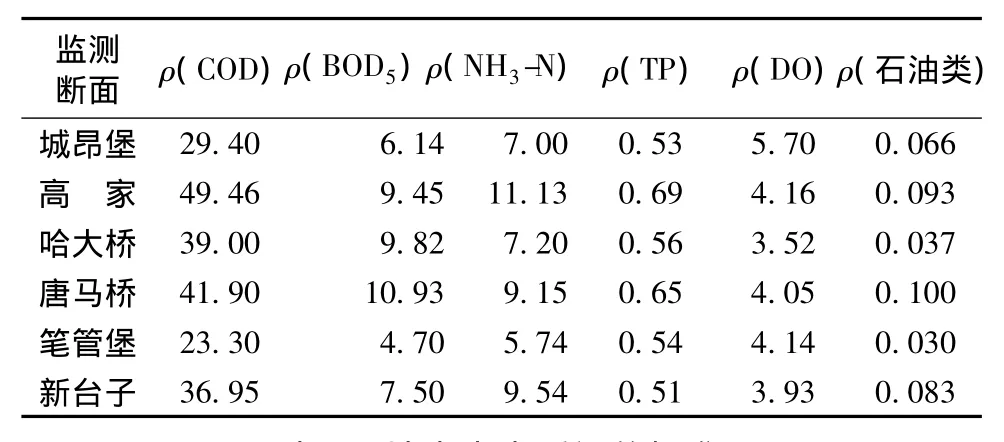
表2 2010年鞍山市城区6个监测断面水质指标监测值mg/L

表3 地表水水质评价标准 mg/L

2.3 评价过程及评价结果

2.3.1 权重计算

鞍山市为著名的老工业基地，地表水污染源主要为工业废水。根据2002—2008年鞍山市水资源公报，鞍山市主要污染物为COD、BOD5和NH3-N，其中NH3-N指标有增长的趋势。根据经验和当地的实际情况，按照二元对比矩阵一致性规则，并对其重要性进行排序，得:

根据各项指标的重要性排序并结合表1的语气算子，计算排序为1的NH3-N指标与其他各指标的模糊标度和相对隶属度，其中与COD和BOD5比较，它们之间的重要性分别为“稍微”与“略微”之间、“略微”与“较为”之间，则它们之间的相对隶属度可分别取0.74、0.6。与排序为5的DO和石油类比较，它们的重要性均在“明显”和“显著”之间，其相对隶属度可均取为0.381。同理与TP比较，重要性为“较为”和“明显”之间，相对隶属度为0.484。则所得的权向量为(0.74，0.6，1，0.484，0.381，0.381)，将其归一化，求得主观权重:

p=(0.207，0.168，0.279，0.135，0.106，0.106)

将规范后的原始数据按式(11)计算，根据熵权法求得客观权重:

q=(0.139，0.18，0.137，0.133，0.204，0.207)

根据式(14)求解最优组合权系数规划模型，用Matlab软件编写程序，利用遗传算法求得最优解为:l*1=0.828，l*2=0.561，将其归一化处理，求得主客观线性系数分别为0.6和0.4，根据式(15)得出最优组合系数下的权重向量:

w=(0.179，0.173，0.222，0.134，0.145，0.146)

则 COD、BOD5、NH3-N、TP、DO、石油类的权重分别为:0.179，0.173，0.222，0.134，0.145，0.146。

2.3.2 评价过程及评价结果

根据实测资料和评价标准可确定可变模糊集的吸引域和范围域及M点值矩阵:

评判xij在M的左侧还是右侧，选取式(2)或式(3)来计算指标i对级别h的相对隶属度矩度。

现以哈大桥断面为例，对于级别h=4计算水质评价指标的相对隶属度。哈大桥断面的指标特征值为:(39，9.82，7.2，0.56，3.52，0.04)，则其相对应的吸引域、范围域和M4点值向量分别为

［a4，b4］=(［20，30］［4，6］［1，1.5］［0.2，0.3］［3，2］［0.05，0.5］)T

［c4，d4］=(［15，40］［3，10］［0.5，2］［0.1，0.4］［5，0］［0.05，1］)T

M4=(27.5， 5.5， 1.375， 0.275， 2.25，0.388)T

当 x31=39，由此判断在 M34点的右侧，a34=20，b34=30，c34=15，d34=40，选用式(2)计算得 μA(x31)4=0.05，同理可计算其他监测点对级别4的相对隶属度矩阵:

类似可得到水质指标对其他级别的相对隶属度矩阵，根据式(5)在a和p的4种不同组合条件下得到归一化综合相对隶属度矩阵，用式(7)计算该地区水质评价结果(表4)。

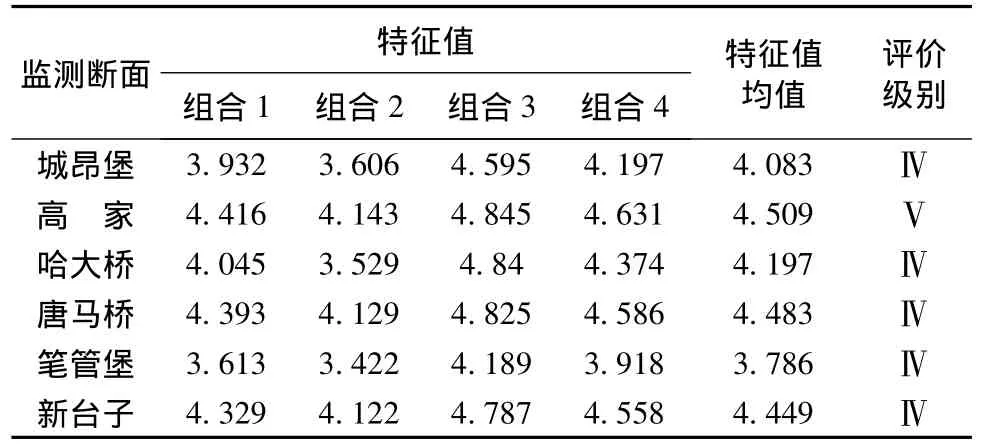
表4 2010年鞍山市城区6个监测断面最优组合赋权可变模糊模型水质评价结果

3 分析和讨论

最优组合赋权可变模糊模型评价结果显示，鞍山市城区6个监测断面地表水水质属于Ⅳ和Ⅴ类的百分比分别为83%和17%，整体水质位于Ⅳ类和Ⅴ类之间，偏向于Ⅳ类水。从实测指标值隶属于评价级别的程度来看，BOD5和COD两个指标位于Ⅳ和Ⅴ类之间，偏向于Ⅴ类;NH3-N和TP为Ⅴ类;DO和石油类位于Ⅱ和Ⅲ类之间，偏向于Ⅲ类(表5)。

表5 各评价指标隶属评价类别百分比 %

根据最优组合赋权确定的权重，NH3-N的权重最大为0.222，其次是 COD和 BOD5，权重分别为0.179和0.173，剩余3项指标TP、DO和石油类权重较为接近，分别为0.134、0.145和0.146。最优组合赋权确定的权重将决策者主观偏好和经验与决策矩阵提供的客观信息有机地结合起来，其权重结果更为科学合理。从最优组合赋权可变模糊模型的评价结果来看，鞍山市城区整体水质偏向于Ⅳ类，与该地区实际情况相符，为进一步验证该模型评价结果的合理性，将评价结果与模糊综合评价法和灰色关联分析法进行比较(表6)。

从所得的评价结果来看，最优组合赋权可变模糊模型的评价结果与模糊综合评判法极为接近，与灰色关联分析法的结果较为接近。模糊综合评价法通过简单的加权法来确定各指标的权重，并根据最大隶属的原则来确定水质级别;灰色关联分析法通过最大关联度确定水质级别;最优组合赋权可变模糊模型将事物之间的模糊程度以量化概念进行表示，并结合离差平方和的最优组合赋权，从而使得评价结果更加客观合理地反映水污染情况。

表6 2010年鞍山市城区地表水水质各评价方法评价结果统计

4 结语

a.本文综合主观权重和客观权重的特点，在标准化数据的基础上，建立基于离差平方和的最优组合模型，确定的最优组合权重有效减少了人为因素对评价结果的影响，使评价结果更为科学、合理。

b.针对水质评价的不确定性，结合可变模糊集理论将最优赋权法应用到可变模糊模型中，与实测值进行分析，结果符合该地区的实际情况;与其他方法进行比较，结果表明评价结果比较接近，从而验证模型的可行性，具有一定的推广意义。

c.本文确定的组合赋权系数在一定程度上克服了主观随意性对权重结果的影响，且根据实际情况需要，可以适当调整主客观权重的向量数量，从而使确定的权重有了合理的依据，提高了最终评价结果的准确度。

［1］邹志红，孙靖南，任广平.模糊评价因子的熵权法赋权及其在水质评价中的应用［J］.环境科学学报，2005，25(4):552-556.(ZOUZhihong，SUNJingnan，REN Guangping.Study and application on the entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment［J］.Acta Scientiae Circumstantiae，2005，25(4):552-556.(in Chinese))

［2］余文忠，唐德善，陆廷春.熵权属性识别法在地下水水质评价中的应用［J］.水电能源科学，2013，31(7):41-43.(YU Wenzhong，TANG Deshan，LU Tingchun.Application of attribute recognition method combined with entropy theory to evaluation of groundwater quality［J］.Water Resources and Power，2013，31(7):41-43.(in Chinese))

［3］杨志英.BP神经网络在水质评价中的应用［J］.中国农村水 利 水 电，2001(9):27-29.(YANGZhiying.Application ofBP neuralnetwork in waterquality evaluation［J］.China Rural Water and Hydropower，2001(9):27-29.(in Chinese))

［4］张海涛，雷晓东，张芳，等.灰色关联度法在盘锦市曙光地区地下水水质评价中的应用［J］.世界地质，2005(24):69-71.(ZHANG Haitao，LEI Xiaodong，ZHANG Fang，et al.Application of degree of grey incidence analysis on groundwater quality evaluation in Shuaguang area of Panjin City ［J］.Global Geology，2005(24):69-71.(in Chinese))

［5］钱会，希文娟.基于AHP权重的模糊评价法在水质评价中的应用［J］.华北水利水电学院学报，2012，33(3):100-103.(QIAN Hui，XI Wenjuan.Application of fuzzy evaluation method based on AHP to waterquality evaluation［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2012，33(3):100-103.(in Chinese))

［6］曾永，樊引琴，王丽伟，等.水质模糊评价法与单因子指数评价法比较［J］.人民黄河，2007.29(2):64-65.(ZENG Yong，FAN Yinqin，WANG Liwei，et al.Fuzzy evaluation method and single index evaluation method［J］.Yellow River，2007，29(2):64-65.(in Chinese))

［7］李国峰，刘宪斌，郭伟华，等.基于主成分分析和水质标识指数的天津地区主要河流水质评价［J］.生态与农村环境 学 报，2011，27(4):27-31.(LI Guofeng，LIU Xianbin，GUO Weihua，et al.Water quality assessment of main rivers in Tianjin based on principal component analysis and water quality identification index［J］.Journal of Ecology and Rural Environment，2011，27(4):27-31.(in Chinese))

［8］穆征，王方勇，李静，等.基于模糊综合评价模型的河流水质综合评价［J］.水利发电，2009，35(4):12-13.(MU Zheng，WANG Fangyong，LI Jing，et al.Comprehensive evaluation of river water quality based on fuzzy comprehensive evaluation model［J］.Hydroelectric Power，2009，35(4):12-13.(in Chinese))

［9］王文川，徐冬梅，陈守煜，等.可变模糊集理论研究进展在水科学中的应用［J］.水利水电科技进展，2012，32(5):89-94.(WANG Weichuan，XU Dongmei，CHEN Shouyu，et al.Research advances and applications in water science of variable fuzzy set theory［J］.Advances in Science and Technology of Water Resources，2012，32(5):89-94.(in Chinese))

［10］陈守煜，胡吉敏.地下水资源承载力评价模糊可变模型与方法［J］.水资源保护，2006，22(6):1-5.(CHEN Shouyu，HU Jimin.Variable fuzzy Cvaluation model and method forcomprehensive evaluation ofgroundwater resources carrying capacity［J］.Water Resources Protection，2006，22(6):1-5.(in Chinese))

［11］金菊良，黄慧梅，魏一鸣.基于组合权重的水质评价模型［J］.水力发电学报，2004，23(3):13-19.(JIN Juliang，HUANG Huimei，WEI Yiming.Comprehensive evaluation model for water quality based on combined weights［J］.Journal of Hydroel Ectric Engineering，2004，23(3):13-19.(in Chinese))

［12］陈伟，夏建华.综合主、客观权重信息的最优组合赋权方法［J］.数学的实践与认识，2007，37(1):17-21.(CHEN Wei， XIA Jianhua.An optimalweights combination method considering both subjective and objective weight information［J］.Mathematics in Practice and Theory，2007，37(1):17-21.(in Chinese))

［13］蒋慧峰，朱文杰.一种最优组合赋权算法［J］.湖北工业大学学报，2007，22(5):78-80.(JIANG Huifeng，ZHU Wenjie.A class of algorithm of optimal combination determining weights［J］.Journal of Hubei University of Technology，2007，22(5):78-80.(in Chinese))

［14］陈守煜.可变模糊集理论与模型及其应用［M］.大连:大连理工大学出版社，2009:56-60.

［15］刘燕，吴文玲，胡安焱.基于熵权的属性识别水质评价模型［J］.人民黄河，2005，27(7):18-20.(LIU Yan，WU Wenling，HU Anyan.Attributerecognition based on entropy weight in evaluation of water evaluation［J］.Yellow River，2005，27(7):18-20.(in Chinese))

［16］WEI Q L，YAN H.A method of transferring polyhedrom between the intersection:form and the sumform ［J］.Computers and Mathematicswith Applications，2001(41):1327-1342.

［17］王应明.离差平方和的多指标决策方法及应用［J］.中国软科学，2000(3):111-113.(WANG Yingming.Mutiindices decision method based on the sum of squares of deviation and application［J］.China Soft Science，2000(3):111-113.(in Chinese))