基于半马尔可夫决策过程的风机变速箱最优维修策略研究

方 冰

(合肥工业大学电气与自动化工程学院，合肥 230009)

发电机、变速箱、叶片与液压元件是风力发电机的核心部分，据相关统计发现，由叶片、变速箱失效导致风力发电机故障的概率达到了79%[1]，风力发电机变速箱在工作中处于高速旋转状态，在压力与磨损共同作用下[2]，其性能和工作效率逐渐劣化，甚至引起整个变速箱故障。

劣化系统的状态维修决策问题是目前设备维护领域的热点问题之一，相关学者对这方面的研究也取得了一定的成果。Byon E和Ding Y把风力发电机系统看作有多种故障模式的多状态退化系统，考虑了自然条件因素，基于马尔可夫决策过程讨论了劣化系统的维修策略优化[3]；Tai A H和Chan L Y研究了考虑维修时间分布的基于预防维修阀值的连续状态维修优化模型[4]；刘华鹏研究了风电机组的变速箱的状态维修，以单位时间费用最低为目标，建立了单部件最优更换时间模型[5]；程志君研究了连续劣化系统的状态维修模型，用Levy过程描述其状态变化，利用更新过程理论解决了此类优化问题[6]。

笔者以风机变速箱为研究对象，将系统连续的劣化过程划分为有限劣化状态，把变速箱随着时间逐渐劣化的过程看成一个Gamma过程，以风机长期运行的单位时间费用为最小为目标，建立基于半马尔可夫决策过程的状态维修[7]优化模型。

1 变速箱随机劣化过程模型①

将风力发电机变速箱系统的劣化过程离散成n个状态，风力发电机组通常采用三级行星齿轮箱(由行星齿轮和三级齿轮组成)，高速运转的齿轮经常会由于磨损、振动、温度过高而发生故障，从而影响整个变速箱的运行状态。把变速箱的劣化过程看成是齿轮磨损程度逐渐累积的结果，设其一段时间内的随机磨损增量服从参数为(γtint,β)的Gamma分布：

(1)

考虑变速箱的状态还受环境的随机冲击影响，假定冲击是在决策时刻点之前瞬间发生的，若冲击前系统状态处于i，冲击可能使状态发生瞬时转移，且转移到j的概率为qij，则[qij]为冲击转移概率矩阵。变速箱系统也可能由于受到环境冲击或者人为失误操作导致其他零部件的性能降低，这样就会增加一项额外费用，并设如果冲击使状态从i转移到j产生的损失费用为cij，则变速箱的劣化过程如图1所示。

图1 变速箱劣化过程示意图

半马尔可夫决策过程一般由六元组组成，具体为{S,A,P(i,j,v(i)),Q(i,j,v(i))，r(i,v(i)),V},其中i,j∈S、a∈A。

状态空间S={1,2,…，i,…,j，…，n}，其中1为叶片完好状态，n为叶片劣化故障状态。

决策A={m,tint}，决策者在离散时刻点T(0),T(1),…,T(n)对叶片和变速箱同时进行检测观察，得到变速箱的状态信息，再根据这一信息采取适当的措施。其中，维修方式记为m={1,2,3,4}={不修，小修，大修，更换}，tint为下一次检测时间间隔。

令发生随机冲击的概率均为μ，设系统经过维修后的状态为k，发生冲击时系统处于状态k′，设X(n)表示决策时刻点T(n)时系统所处的状态，X(n+1)表示决策时刻点T(n+1)时系统所处的状态。令v∈Ωs，Ωs是全体平稳策略的集合，v(i)表示在决策时刻点T(n)时采取的决策，运行如图2所示。

图2 变速箱运行过程示意图

则变速箱的状态转移概率矩阵可表示成：

P(i,j,v(i))={X(n)=i,X(n+1)=j,v(i)=(m,tint)}

(2)

其中[pik]表示系统经过维修后的转移概率，[pkj]表示系统自然运行时的转移概率矩阵，称为自然转移概率，其表达式为：

(3)

(4)

且两个决策时刻间隔时间分布函数为：

(5)

代价函数表示当前决策时刻系统状态处于i，采取策略v(i)，直到下一个决策时刻系统产生的总成本。由每次检测变速箱的费用cins、维修费用cm、冲击损失费用cij、系统单位时间的停机损失费用c和系统处于劣化状态k的单位时间损失费用c(k)组成。变速箱系统的代价函数在叶片维修决策模型的基础上增加了一个冲击损失费用。

若未发生随机冲击，代价函数表示为：

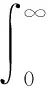
λj-1c(j)tint/(λk-1+…+λj-1)

(6)

若发生了随机冲击，代价函数表示为：

λk′-1c(k′)tint/(λk-1+…+λk′-1)+ck′j

(7)

准则函数：设α为折扣因子且0<α<1，r(X(n),v(X(n))表示Tn→Tn+1时间内的单位时间期望代价，则无限阶段的系统平均代价准则可表示为：

(8)

2 Q学习算法

Q学习算法是一种基于随机动态过程的强化学习常见方法[8，9]，适用于模型信息不完全可知的马尔可夫系统和半马尔可夫系统的决策问题，其基本思想是通过样本轨道学习并更新所有可能的状态行动对的函数值Qα(Xn,v(Xn))。

根据性能势的特点可以得到系统在折扣和平均准则下统一的计算公式，即Q因子的即时差分公式可表示为：

(9)

w(n)=T(n+1)-T(n)

(10)

(11)

ηn=(1-γn)ηn-1+γnf(Xn,v(Xn))

(12)

其中，γn为学习步长，则Q因子的迭代公式为：

Qα(Xn,v(Xn))=Qα(Xn,v(Xn))+γndn

(13)

经典的Q学习算法通常采取贪心策略的思想进行探索利用，前面介绍的半马尔可夫决策过程的状态维修优化模型为该算法在维修决策问题中的运用提供了可靠的理论基础。

3 仿真实例

以FL-2500风力发电机作为研究对象，将变速箱的劣化过程离散成为5个状态，即S={1，2，3，4，5}，假设变速箱系统的各非故障状态的逗留时间均服从参数λ=0.002的指数分布，设齿轮单位时间磨损增量服从参数为β=0.0001的指数分布，每次的检测费用为cins=50，小修、大修、更换的维修费用分别为3 000、7 500、150 000元，即cm={0，3 000，7 500，150 000}，小修、大修、更换的维修时间分别服从参数μm为0.5、0.2、0.1的指数分布，5个状态单位时间损失的费用依次为0、50、100、150、200，即c(k)={0，50，100，150}，且故障状态损失的单位时间费用也就是停机损失的单位时间费用设为c=200。设变速箱各状态下发生环境冲击的概率均为μ=0.001，并将冲击使得发生状态转移的概率和产生的单位时间损失的费用分别为：

(14)

(15)

根据前面介绍的策略迭代算法和Q学习算法，并利用Matlab7.1进行编程求解得到平均准则下的仿真结果(图3、4)。

图3 变速箱模型的策略迭代优化曲线

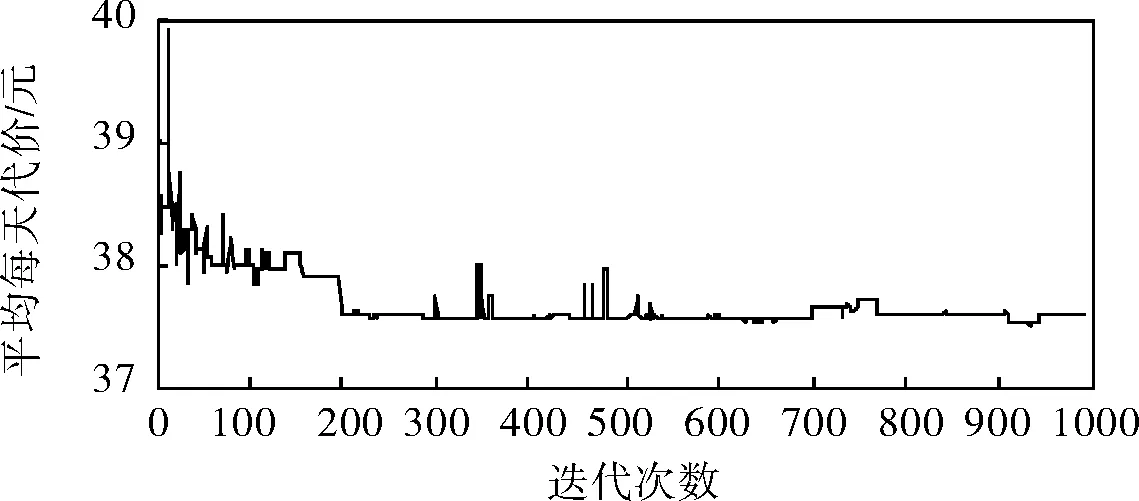
图4 变速箱模型的Q学习优化曲线

通过策略迭代算法和Q学习算法得到的变速箱系统的最优单位时间(每天)费用为37.61元，最优维修策略为：v*={(1,281),(2,217),(2,60),(3,205),(4,281)}。将几个不同检测时间间隔值进行若干次仿真数据后整理得到检测时间间隔与费用率的关系图(图5)。可以从最优维修策略中看出当变速箱系统处于中间状态3时，其检测时间间隔比其他劣化状态下的检测时间间隔小很多，这是因为在状态3时进行小修可以使系统恢复到状态2，而状态2的检测时间间隔较

图5 检测时间间隔与费用率的关系

长，劣化单位时间费用较低，且回到完好状态也只需小修，若在状态3采取大修或者更换，其昂贵的维修费用可能导致得不偿失。

4 结束语

针对离散状态的半马尔可夫决策过程的状态维修模型，建立风力发电机变速箱的Gamma过程劣化模型，并且通过理论仿真和学习仿真对模型进行求解分析，证明了模型的经济性和有效性。对于连续状态的情况，仍需要进一步的研究与讨论。