基于EMD与GA-BP网络的离心泵汽蚀故障诊断
2014-08-03周云龙
周云龙 吴 昱
(东北电力大学自动化工程学院,吉林 吉林 132012)
汽蚀是离心泵经常发生的故障之一,汽蚀的发生会给离心泵的正常运转带来损害,如改变泵的正常工况、降低其运行效率,此外,长时间的汽蚀会造成叶轮等过流部件的损坏[1]。离心泵进、出口压力信号的改变能反映汽蚀的发展程度,可作为诊断汽蚀的诊断依据。通过理论研究和实际采集情况得知该信号不是线性、平稳信号。传统的傅里叶变换和基于傅里叶变换的一些信号处理手段,如短时傅里叶变换、魏格纳分布及小波变换等,因其研究前提是假设信号为平稳或分段平稳,且受到不确定原理的限制,较为适合分析线性、平稳信号。经验模态分解(EMD)是基于信号的局部特征时间尺度,将信号分解为若干本征模态函数(IMF)和的形式。每一个IMF都能体现各自不同频率和时间尺度下的特性,更能突显原始信号的局部特征[2]。因此EMD分析方法非常适合分析离心泵的入口压力脉动信号。
为了使汽蚀实验精确、全面,在实验过程中采用变频器调节流量,将得到的特征向量作为样本输入到BP网络中学习,提高故障诊断的准确率。
1 方法和原理①
1.1 EMD
1.1.1EMD原理
EMD方法是将信号分解成若干本征模态函数和的形式,是建立在一定的假设基础之上的[2~6],其中任意一个基本模式分量都满足以下条件:
a. 全部信号段中,信号必须满足信号段内极值点的数量等于交叉点的数量,或者信号中极值点、交叉点数量保持一致;
b. 时间轴上的任意一点所对应的上、下两条包络曲线代数均值为零,也可以理解为两包络曲线关于时间轴是对称的。
EMD分解是把不平稳信号转化成平稳信号。分解得到的若干本征模态函数可以看作是按照原始信号频率从高到低“裁剪”得到的。
1.1.2特征提取算法
在不同的有效汽蚀余量下运转的离心泵,其对应的入口压力脉动信号的能量也会相应改变。为了更具体地把握其变化情况,这里采用IMF能量比来表示。现作以下定义:
(1)
(2)
(3)
式中ai(t)——各IMF的幅值函数;
N——每个IMF的数据点。
1.2 GA-BP神经网络
1.2.1原理
BP网络在故障诊断分类中的广泛应用得益于其具有寻优精确性高的特点,但在使用BP神经网络的过程中也发现了这种学习算法的缺陷,如训练速度慢和存在局部最优化的问题。遗传算法是基于生物进化理论的一种自适应优化方法,具有极好的鲁棒性,也具有更好的寻找到最优解的能力[7,8]。笔者介绍的GA-BP是遗传算法和神经网络的优化算法[3]。通过GA对BP网络的权值和阈值进行优化,把优化后的网络应用到汽蚀故障诊断中去,利用了BP网络预测等功能的同时避免了其局部最优化等问题,在处理这一类问题中有着一定的优势。
1.2.2特征提取算法
BP神经网络由输入层、输出层和隐含层构成,可以看成一个规模宏大的并行处理器。BP神经网络具有较强的对环境的适应性和学习能力。笔者所使用的三层BP网络的结构如图1所示。

图1 BP网络结构
图1中x1,x2,…,xn为输入层;xi与隐含层yj的连接权记作V;W是输出层节点和yj的连接权值。用GA算法优化BP神经网络,过程如下:
a. 初始化。采用实数编码,避免了编码和解码过程,便于大空间意义上的搜索,提高计算精度。确定群体规模、突变概率,确定交叉规模和交叉概率、最大迭代次数和终止进化条件。

c. 除去样本外增加的个体是由Gi与Gi+1交叉获得的。不进行此操作的个体在自我复制后进行下一步操作,其中交叉操作的概率为PC。
d. 变异。在较小的突变概率Pm下突变产生新个体Gj,要求变异概率随着最优个体不变指数的上升而增加。初始值变异概率为0.001。
e. 将交叉操作和突变原因产生的新个体重插入到种群P中,这种替代方法称为重插入,并计算新个体的评价函数。
f. 计算个体适配度,当满足优化条件E(i)≤εGA时,则将结果的最优个体作为优化网络的系数。如果不满足条件,重新执行交叉和变异操作直到得到满足条件的值。
2 实验装置和步骤
2.1 实验装置
实验装置如图2所示,采用的是气蚀闭式实验台。采用卧式单级离心泵,型号为ISW40-100;泵轴与电机相连成为一体;叶轮为闭式,直径1m;离心泵的出、入口直径均为4cm;离心泵在额定工况下流量Q为5.6m3/s,扬程为10m,额定转速2 900r/min;和离心泵入口直接相连的透明管长0.5m,用以对汽蚀状态进行实时观测;真空泵和水箱直接相连,用来改变密闭水箱内的压力。实验台所采用的JC2WY-40涡轮流量计准确度约0.3%,能够满足实验要求。压力变送器为JYHR-101系列压力变送器。

图2 实验装置简图
2.2 汽蚀信号的采集
信号采集时,先通过变频器将离心泵调至某一流量,待流体流动稳定后,采集入口压力脉动信号,记录流量等参考数据,该数据为离心泵在正常运行状态下的参考值。完成上述步骤后,启动真空泵,通过对水箱内部压力进行调节来改变离心泵的工况。泵有效汽蚀余量会随着泵体内部压力的降低而逐渐降低,使得离心泵分别工作在汽蚀初生、轻微汽蚀和严重汽蚀3种状态下,并按上述方法采集离心泵的入口压力信号。采集完成后将流量变化及有效汽蚀余量等数据记录作为一组。然后重复以上操作记录不同流量下的汽蚀状况。实验共采集6个流量下的入口压力信号。
2.3 汽蚀工况判据
汽蚀工况的判据如下:
a. 正常运行。观察段内为全液相流体,流体流动过程中并无气泡产生。
b. 初生汽蚀。透明管观察段内液体流动中出现少量细小的气泡且气泡有向低压区扩散的趋势。
c. 轻微汽蚀。透明观察管段内液体气泡增多,出现连续、小体积、比较均匀分布的气泡。
d. 严重汽蚀。透明段气泡体积急剧增加形成的汽液两相流充满整个管道;泵体振动剧烈,噪声进一步增强。
3 实验结果及分析
以额定流量下正常运行、初生汽蚀为例,对信号进行EMD分解,结果如图3所示。表1是额定流量下各IMF的能量比。从表1和图3中看出,正常运行时能量主要集中在第2、7两层,而初生汽蚀和以后状态的能量主要集中在第2、6、8层。

图3 额定流量下正常运行、初生汽蚀EMD分解比较

IMF12345678正常0.6837.882.989.9910.102.9935.850.70初生0.034.990.030.010.025.010.0290.02轻微0.015.020.010.020.014.980.0190.04严重0.015.010.010.030.034.920.0289.99
观察表1可知,第5、7层能量比在发生汽蚀时明显降低,第6层在不同状态的变化不是很明显,第8层能量比有明显升高趋势,表明低频能量比在不同状态时有明显的不同。文献[2]指出:离心泵发生汽蚀时,在不同的汽蚀状态,低频能量的变化具有参考价值。笔者从低频能量比来分析离心泵的汽蚀特征。表2为不同流量下IMF能量比的比较。

表2 不同流量下各IMF的能量比比较
由表2纵向比较得知:由正常运行到初生汽蚀,第8层能量比增至原来的40倍左右,第6、7层能量比降至原来的40%左右;由初生汽蚀到轻微汽蚀,第8层能量比增至原来的1.5倍左右,第7层降至原来的50%左右;由轻微汽蚀到严重汽蚀,第5、7两层降低十分明显。横向比较得知:在不同流量下,IMF5~8层的能量比变化不大。这说明IMF5~8层的能量比与离心泵的汽蚀状态有关,可以作为特征值进行网络训练。
GA-BP网络的建模过程如下:
a. 获得输入样本。将IMF5~8层的能量比形成4维能量分布向量,选取4种状态各50组特征向量输入到GA-BP网络中进行训练。
b. 确定输出模式。4个输出神经元的状态分别为正常运行、汽蚀初生、轻微汽蚀和严重汽蚀且输出值为1时表示属于此类故障,输出值为0时表示不属于此类故障。数值大小在0和1之间,数值的大小也反映了属于此类故障可能性的大小,即正常运行输出为[1 0 0 0]T,汽蚀初生为[0 1 0 0]T,轻微汽蚀为[0 0 1 0]T,严重汽蚀为[0 0 0 1]T。
c. 选取激活函数。综合笔者的研究内容,输入层和输出层的数值大小在0和1之间,满足对数S形函数的输出情况,由此选择对数S形函数作为激活函数,也利于学习算法的收敛。
d. 训练精度设置为0.000 1。训练完成时,随机选取20组各种工况下的实验数据用以检测网络。得到的网络训练误差如图4所示,汽蚀情况的识别结果见表3。
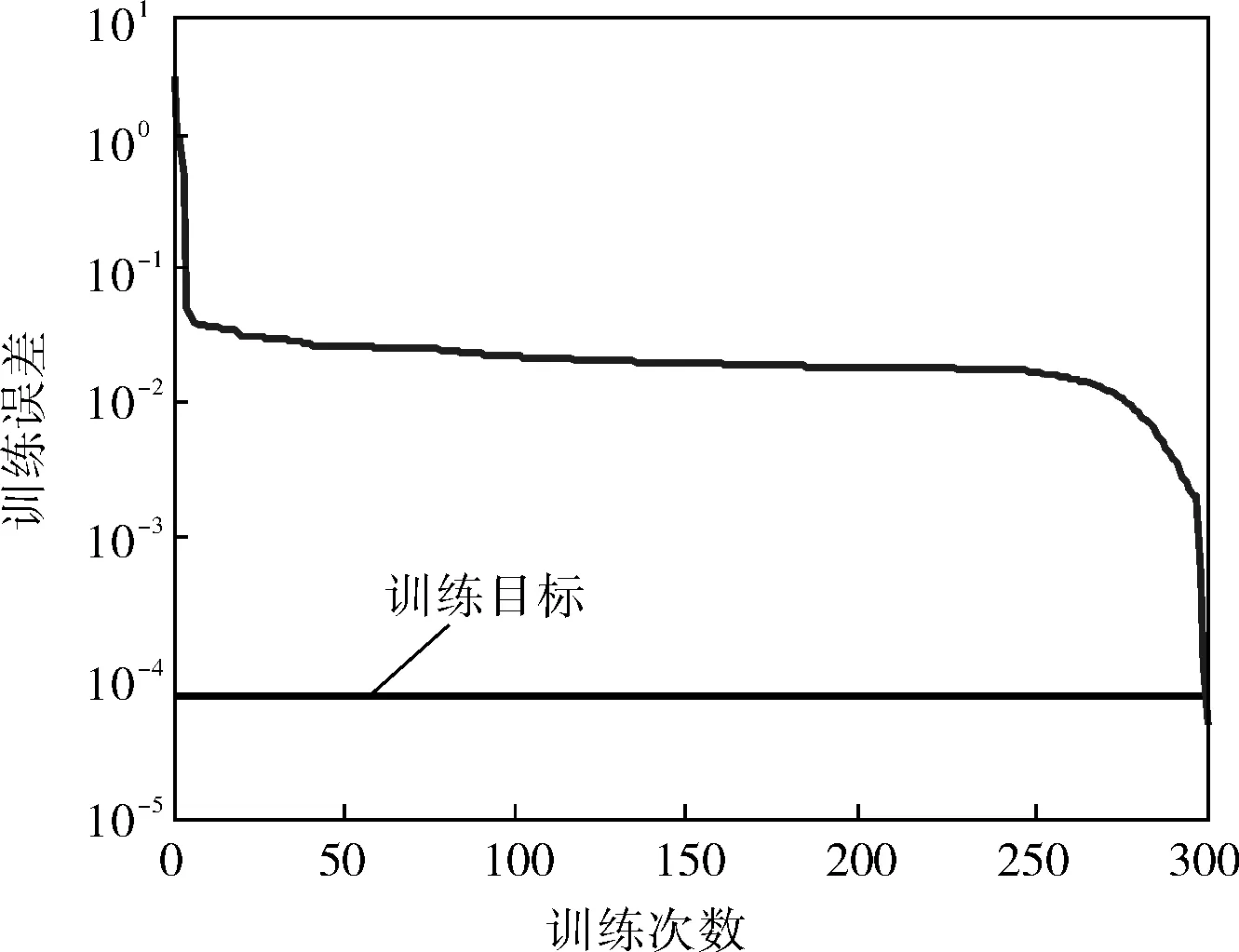
图4 GA-BP网络训练误差

IMF5678期望输出正常0.9970.000 20.000 00.000 11000初生0.0010.988 20.000 20.000 10100轻微0.0000.000 00.999 40.000 00010严重0.0000.000 20.000 00.986 30001
从表3可以看出,利用EMD与GA-BP神经网络对离心泵汽蚀状态进行诊断识别,取得了很好的效果,实验结果也表明,所选取的特征向量能很好地描述汽蚀信号的信息。
4 结束语
经验模态分解是一种有效的压力波动信号特征提取方法。离心泵汽蚀故障信号经经验模态分解后的低频能量比与汽蚀状态有关,从而可以构成汽蚀故障诊断的特征向量。经验模态和GA-BP神经网络相结合,对离心泵汽蚀状态有很高的识别精度。
