基于二进小波变换的多尺度边缘细化检测

刘继承 张 琳 董青松 石祥华

(1.东北石油大学，黑龙江 大庆 163318；2.大庆油田天然气分公司，黑龙江 大庆 163000)

边缘检测技术在图像分析与识别领域至关重要，寻找一种最优边缘检测算法是近年来此领域的热门课题之一。边缘检测是通过检测图像区域间的变化实现的，这些变化有灰度、颜色及纹理特征等。通常是将彩色图像转换为灰度图像，再利用传统的边缘检测算子(如一阶微分算子——Prewitt算子、Roberts算子和Sobel算子，及二阶微分算子——Laplace算子等)，计算梯度的幅值和方向。这些算子易于实现，而且实时性好，但是在抗噪和单像素边缘定位方面效果不太好，尤其是对噪声的干扰非常敏感。上述算法中，基于多尺度小波分析的图像边缘检测算法在抑制噪声和提取边缘定位方面表现良好，受到了国内外学者的广泛重视[1]。1983年有学者提出尺度空间思想，对边缘检测中的多尺度和多分辨进行了深入研究。1992年又有学者提出小波变换多尺度边缘检测方法，同时将小波边缘检测方法与LOG算子和Canny最优检测算子在小波意义下统一，更明确地表达了多尺度思想在边缘检测中的重要意义[1]。

多尺度小波变换图像边缘检测算法存在的问题是大尺度下图像边缘细节信息会有丢失，导致检测到边缘点定位不准确而偏离实际边缘；小尺度下图像边缘点又易受噪声影响导致检测到伪边缘[2]。选取合适的尺度并采用合理的边缘细化算法是平衡多尺度下边缘检测优/缺点的主要思路。笔者在多尺度小波变换得到的边缘灰度图像中选择最优尺度灰度图像，再选择合适的灰度门限，将图像转换为二值图像后，用边缘细化算法将边缘准确定位到单像素宽度，以期较传统边缘检测算子在噪声容限和单像素边缘定位方面有所提高。

1 多尺度边缘检测①

对于一幅普通图像而言，边缘就是图像颜色或灰度发生突变之处，边缘检测的目的就是检测出图像中突变发生的位置。传统的边缘检测算子对图像进行边缘检测的基本原理就是求微分运算，找到图像中的突变点作为图像边缘，原理简单、操作容易，但是存在的最大问题就是对噪声敏感。

较好地解决噪声敏感问题的方法之一是对图像进行多尺度边缘检测，这需要首先对图像进行多尺度表达。对图像进行小波变换是获得图像多尺度表达的一种方法，小波变换能够把图像分解成多种尺度成分，并对大小不同的尺度成分采用相应的时域或空域取样步长，从而不断地聚焦到图像的任意微小细节、间断点、奇异点和边缘[3]。小波变换所独有的这种多尺度特性恰好可以用于多尺度下图像的边缘检测[4]。人在观察目标时，随着分辨率的增加，越走近目标观察获得的信息就越丰富；反之，获得的信息越少[5]。在噪声抑制与图像细节表现之间寻求平衡是多尺度分析的主要任务。由于小波变换在各尺度上都提供了图像的边缘信息，所以称为多尺度边缘，小波变换是提取多尺度边缘的基础。

2 图像小波变换

小波变换是将一个函数表示为一个尺度成分和这个尺度下的一个小的波动成分的一种运算。

2.1 连续小波变换

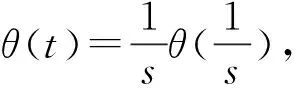
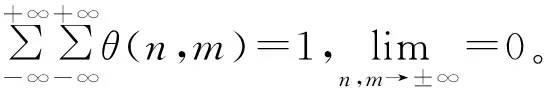
对每个像素点(n,m)计算相角Af(2j,n,m)的正切值：

2.2 求边界点

确定阈值T>0，对于Mf(2j,n,m)，如果Mf(2j,n,m)≥T，Mf(2j,n,m)取得局部最大值，即此时的(n,m)为模极大值点。因为梯度的局部极大值对应着图像f(n,m)的锐变处，而且图像的边缘也处于图像的锐变处，所以图像f(n,m)的梯度局部极大值点就对应着图像的边缘点[7]。

局部梯度幅值最大就是图像的局部高频信息，图像的噪声也是局部高频信息，经过小波变换后也可能产生边缘，这种边缘为伪边缘。图像进行小波变换后无论在哪个尺度上，尖锐边缘都有很大的信号值；相反，噪声点的信号值会随着尺度的增大而衰减[8]。

从图1所示的实验结果可以看出：随着尺度的增大，图像的细节逐渐减少消失，边缘逐渐平滑。这正是多尺度小波变换对高频信息进行平滑滤波的体现。但同时也存在图像细节丢失的缺陷，直观感觉就是图像变模糊。

图1 实验结果

3 边缘细化

经小波边缘提取得到的图像边缘比较粗，难以达到单像素的精度，需要对图像的边缘进行细化。图像边缘细化是图像处理中的基本技术，它要求完整地保存图像的拓扑结构，以便于代替原始图像进行识别和处理。将一个图像的主要边缘清晰、完整地提取出来，得到细化的、完整的边缘，将为图像检索、目标分割及识别等后续处理带来极大的便利[9]。

此处的边缘细化算法采用改进的Zhang-suen算法，其基本思想是在细化过程中不断移动3×3的模板，使它与图像中的各点重合。在扫描图像的过程中，定义待删除的像素为P1，P1周围的近邻像素位置关系如图2所示。

定义n(P1)和s(P1)两个参数，其中n(P1)是与P1相邻的非零像素个数，s(P1)是沿着P2→P3→P4→P5→P6→P7→P8→P9→P2的顺序由0过渡到1的总次数。对于考察点P1=1，如果同时满足2≤n(P1)≤6、s(P1)=1、P2P4P8=0且P2P6P8=0这4个条件，则可将P1删除。细化过程是将满足条件的像素点予以删除。反复迭代直到再也没有像素点满足上述条件为止，此时完成检验，得到了细化后的图像边缘。这样，所有检测到的边缘可以定位到单像素宽度，完整地保留了图像的边缘信息[10]。

4 实验结果比较分析

图3给出了不存在噪声时，传统边缘检测算子检测的结果。

图3 无噪声图像传统边缘检测结果

由图3可以看出，传统的边缘检测算子在没有噪声的情况下可以得到较好的边缘检测效果。实际的数字图像总是存在一定功率的噪声，如椒盐噪声及高斯噪声等，其中椒盐噪声可以通过中值滤波较好地去除，高斯噪声是图像噪声容限方面要考虑的主要噪声。图4给出了存在高斯噪声(μ=0,σ=0.01)时传统的边缘检测算子的检测的结果。

图4 传统方法检测的含高斯噪声图像结果

可以看出，在有高斯噪声存在的情况下，传统的边缘检测方法检测的图像边缘出现缺失，伪边缘被检测出大范围出现，对边缘检测结果造成了极大破坏。采用基于二进小波变换的多尺度边缘细化检测方法检测得到的边缘如图5所示。

从视觉直观感受来看，加入高斯噪声的传统边缘检测方法的检测结果受噪声干扰很大；而采用笔者提出的方法后，图像边缘的连续性和准确性都比传统方法的检测结果有较大改善。

图5 检测结果

在此，定量地来探讨图像边缘检测结果的比较。边缘检测过程会产生3个主要类型的误差，即边缘点丢失、边缘点定位偏离以及将噪声波动误认为是边缘点。以Canny最优边缘检测准则为参考依据，Canny最佳边缘检测三准则具体如下：

a. 最优检测。对于真实存在的边缘不漏检，当然也不会把非边缘点检出，使得输出信噪比最大。

b. 最优检测精度。所得边缘点的位置与实际边缘点的位置最近。

c. 检测点与边缘点一一对应。每个实际存在的边缘点与检测到的边缘点一一对应。

信噪比SNR越大，能够准确检测到的真实边角和较少含有伪边界的可能性也就越大。检测精度L为检测到的边界与真实边界之间倒数的数学期望，检测精度越高，测量误差越小。伪边界平均距离M为随机噪声与检测函数卷积之后伪边界出现的平均距离，伪边界平均距离越长测量结果中出现伪边界的个数就越少[12]。

以主要性能指标信噪比SNR作为边缘检测评价标准，将没有噪声存在时的Canny边缘检测算子检测的边缘作为实际边缘，与存在(μ=0,σ=0.01)高斯噪声时传统的最优边缘检测算法Canny边缘检测和笔者所提方法进行比较，Canny边缘检测的SNR=1.005 0，小波多尺度边缘检测的SNR=1.534 8。

5 结束语

笔者研究了基于二进小波变换的图像多尺度边缘检测及其边缘细化算法，在与传统边缘检测方法进行比较的基础上，对传统方法在无噪声和有噪声存在时边缘检测的结果进行比较，并就笔者所提方法与传统边缘检测方法的标信噪比进行了定量分析。实验结果表明：基于二进小波变换的图像边缘提取细化算法较传统边缘检测方法在噪声容限和边缘细化到单像素宽度方面有明显改善。与传统边缘算法相比，小波变换边缘检测细化算法具有定位精确和计算量小的优点，对噪声的敏感程度也远低于传统边缘算法。