通过“染色问题”，培养中学生化归思维*

赵 广 乐，闫 春

(1.包头市第一中学，内蒙古 包头 014040；2.大连民族学院 国际商学院，辽宁 大连 116650)

对于大多数的高中学生而言，排列组合部分的染色问题很是繁难！众所周知，染色问题大多需要分类讨论！可是以什么为标准进行分类讨论？又要分为多少类？并无统一的解决方式，这也正是染色问题的繁难所在！

事实上，我们完全可以通过递归方法，求出一类基础染色问题的通项公式，然后将其他的染色问题化归(转化、归结)为该染色问题即可！

例1:(扇形结构染色问题)如图1所示，用m种颜色给n块扇形染色，要求相邻不同色，求证：染色方法总数为(m-1)n+(-1)n(m-1)。

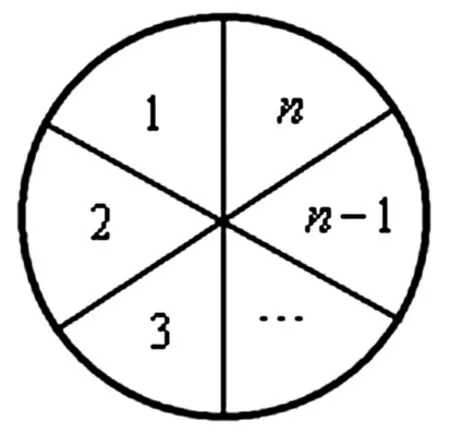
图1

证明：设用m种颜色给n块扇形染色，相邻不同色，染色方法总数为an。

由分步计数原理可知染色方法总数(若不考虑第一块与第n块是否同色)共有m(m-1)n-1。

第一块与第n块可能同色可能异色，若同色，则相当于按题目要求染了n-1块扇形区域；若不同色，则按题目要求染了n块，由分类加法计数原理可知an+an-1=m(m-1)n-1⟺an=m(m-1)n-1-an-1。

两边同时减去(m-1)n

⟹an-(m-1)n=-[an-1-(m-1)n-1],

令bn=an-(m-1)n，有bn=-bn-1,b2=m-1

⟹bn=b2(-1)n-2=(-1)n-2(m-1)

=an-(m-1)n

⟹an=(m-1)n+(-1)n-2(m-1)

=(m-1)n+(-1)n(m-1)

为了方便起见，我们可以简记为：

an=(色-1)块+(-1)块(色-1)块。

至此，我们求出了排列组合扇形染色问题的一般解，从而避免了分类讨论的繁杂！

至于其他类型的染色问题，大多数可以化归为扇型结构染色问题。

例2:用4种颜色给如图2的5块区域染色，则不同的染色方法有______种？

然后将区域1挖走，即将题目化归为了用3种颜色给图3的4块区域染色，由扇型结构染色公式：(色-1)块+(-1)块(色-1)

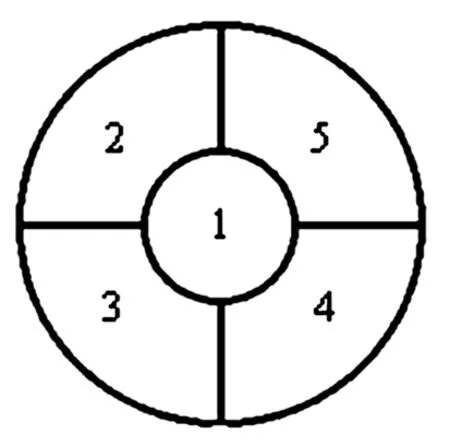
图2

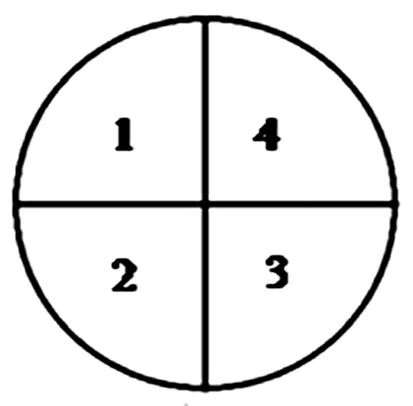
图3

可知染色方法共有：

(3-1)4+(-1)4(3-1)=16+2=18

综上，由分步计数原理可知，染色方法总数为4×18=72种。

例3:一个地区分为五个行政区域，现用四种颜色给地图着色，要求相邻区域不同色，则同的染色方法有______种？

解析：将地图进行拓扑变形见图4，以实现化归。

即将题目转化为例2，用4种颜色给5块区域染色，则不同的染色方法数为72种。

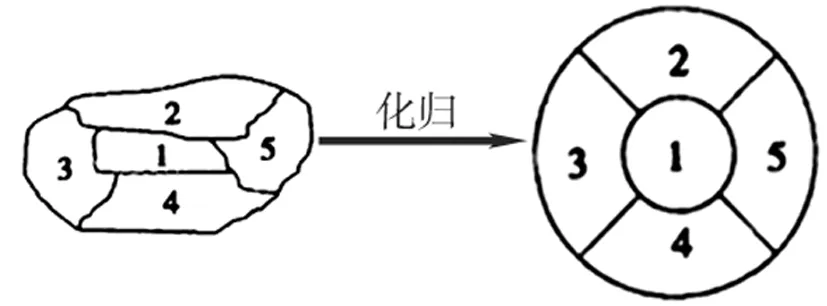
图4

例4:用5种颜色给四棱锥的5个顶点染色，要求同一棱的两端异色，则不同的染色方法有____种？

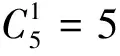
图5

由上述几例可以看出，一般的染色问题要化归为扇形染色问题，重要的不是颜色的种数，不是区域的编号，而是区域的相邻关系(位置)。换言之，只要相邻关系相类似，即可通过变形实现彼此化归。这也正突出了现代数学的本质：研究结构、范畴、模式的科学。

事实上，人类解决任何问题，都是一个化归的过程。面对一个陌生的问题P，人们总是在脑海(书籍、网络)中搜索相类似的、简单的、易于解决的或解决过的问题Q，一旦找到，即可将这个陌生的问题P化归为较易解决的问题Q。即便不能直接实现化归，人们也能通过问题Q的解决，来类似地解决问题P。

例5:

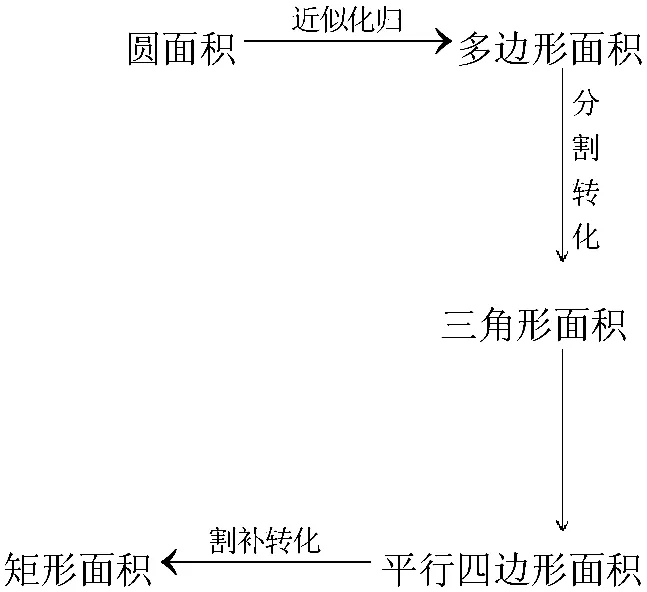
(原始命题)

例6:

例7:一元二次方程ax2+bx+c=0(a≠0)的求根公式：

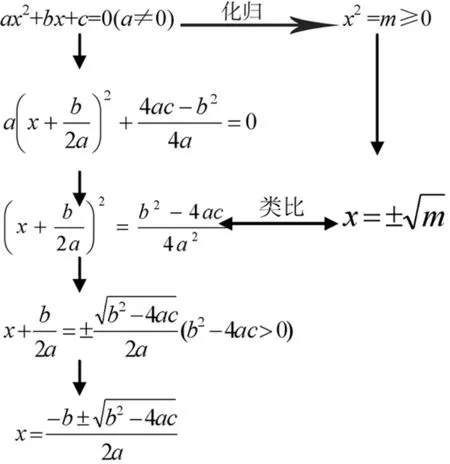
正如匈牙利著名数学家Rozsa.Peter用以下比喻十分生动地说明了化归思维的实质。“假设在你面前有煤气灶、水龙头，水壶和火柴，你想烧些开水，应该怎么去做？”正确的回答是：“在水壶中放上水，点燃煤气，再把水壶放到煤气灶上。”现在又有一个问题：“如果其他的条件都没有变化，只是水壶中已经有了足够的水，这时你又应该如何去做？”这时，人们往往会回答：“点燃煤气，再把水壶放到煤气灶上去。”但数学家不会这样去做，数学家只需要倒掉水壶中的水，并声称已经把这个问题化归成了前面已解决的问题了。 “把水倒掉——简洁而有效的回答。”Rozsa.Peter同时还指出“化归思维，正是数学家与其他科学家的最大区别之所在”。

例8:法国著名数学家、解析几何之父笛卡尔(Rene.Descartes)曾提出一个“万能方法”，即将一切问题化归为数学问题，将一切数学问题化归为代数问题，将一切代数问题化归为方程求解问题。虽然用这一方法解决所有问题是不可能的，但笛卡尔

依然用这一思想方法创立的解析几何。解析几何的创立是数学发展史上的丰碑，开创了用代数方法研究几何问题的新纪元。恩格斯对此曾经作过评价“数学中的转折点是笛卡尔变数，有了变数，运动进入了数学；有了变数，辩证法进入了数学；有了变数，微分和积分也就立刻成为必要的了，……”。

↓ ↓

让我们再回到染色问题。

例9:用5种颜色给四棱锥的5个面染色，要求有公共棱的两个面异色，则不同的染色方法有____种？

解析：将四棱锥沿AB,AC,AD,AE展开成平面图形，见图6。

图6

即将题目转化为例4，用5种颜色给5块区域染色，则不同的染色方法数为420种。

例10：用6种颜色给正方体的6个面染色，要求有公共棱的面不同色，则不同的染色方法有____种？

解析：将正方体从顶面A处扒开(扒橘子皮),见图7。

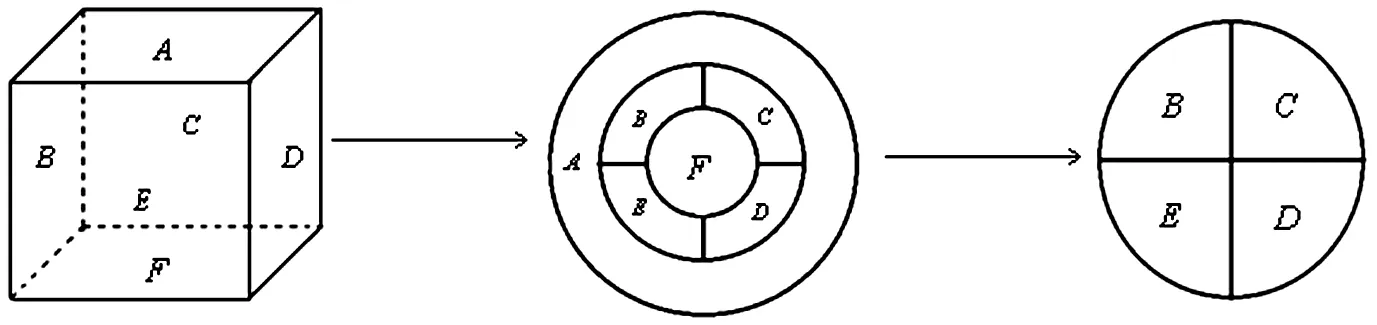
图7

若A,F同色，则染色方法数为

若A,F异色，则染色方法数为

综上，染色方法总数为:1560+2520=4080。

例11：用6种颜色给四面体的6条棱染色，要求有公共顶点不同色，则不同的染色方法有______种？

解析：仔细分析四面体6条棱的相邻关系，其每条棱与另外5条棱中的4条相邻，其相邻关系类似于例10(每个面与其余5个面中的4个面相邻),见图8。

即将题目化归为例10，知其染色方法数为4080。

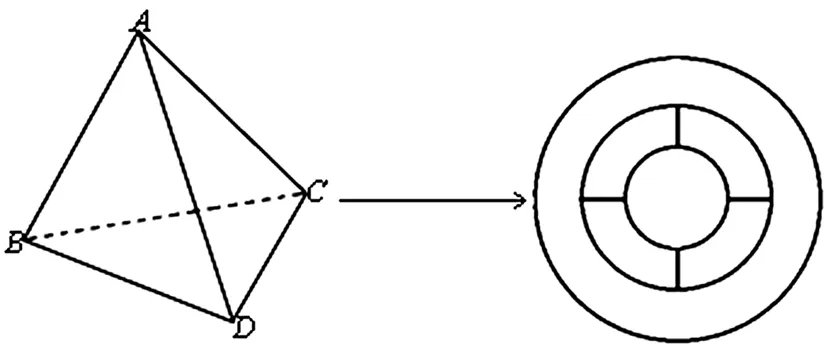
图8

通过上述几例我们可以看到：化归思想的实质就是通过事物内部的联系和矛盾运动，在转化中实现问题的规范化、模式化，即将复杂转化为简单，将困难转化为容易，也就是“打不赢就跑，跑到打得赢的地方再打”。

当然，并非所有染色问题都可以化归为扇型结构染色问题，如下面几例。

例12:恰用5种颜色给图9的5块区域染色，要求相邻的区域不同色，则不同的染色方法有______种？

解析：本例虽然结构可以转化为扇型结构染色，但题目要求恰用5种颜色染色，而非扇型结构染色问题的可用小于等于5种染色颜色。因此，本例无需转化为扇型结构染色问题，直接排列即可解决。

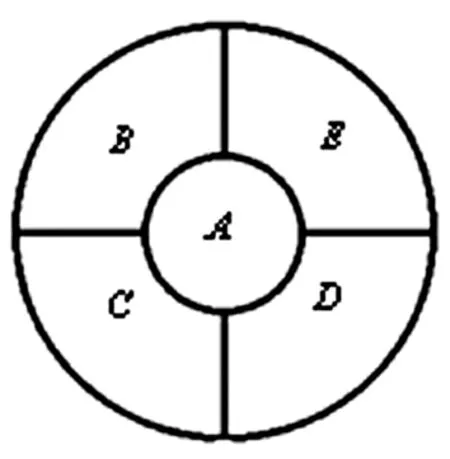
图9

例13:用4种颜色给图10中A,B,C,D,E,F6个点染色，每条线段的两个端点不同色，则不同的染色方法总数有______种？

解析：本例的染色结构，无法化归为扇形结构，故只能分类讨论，各个击破。

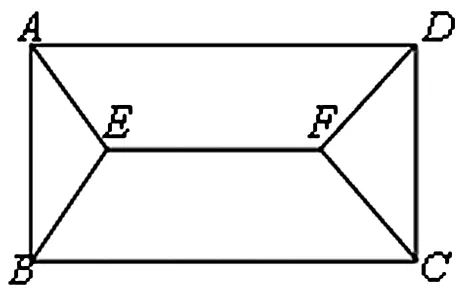
图10

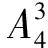
综上，共计有48+216=264种不同的染色方法。

由上述两例我们可以看到，化归方法也并非万能方法。事实上，万能方法是不存在的！尽管如此，化归方法作为人类解决问题最重要的思维模式，应该受到广大师生的重视！正如日本数学教育家米山国藏所说“学生们在初、高中所学的数学知识因毕业后几乎没有什么机会应用，通常在走出校门后不到一两年很快就忘记了。然而不论他们从事什么工作，深深铭刻于头脑中的数学精神、数学思维方法、研究方法、推理方法和着眼点却随时随地发生作用，使他们终身受益。”化归思维就是学生们在将具体数学知识忘记之后，应该铭刻于其头脑之中，使之受益终生的思维模式。

〔参考文献〕

[1]赵小云,叶立军．数学化归思维论[M] ．北京：科学出版社，2006.

[2]杨世明．转化与化归[M] ．哈尔滨：哈尔滨工业大学出版社，2012.

[3]史久一、朱梧槚．化归与归纳、类比、联想[M] ．大连：大连理工大学出版社，2008.

[4]寇玉贵．排列组合中的染色问题[J] ．青海教育，2008,45(4).

[5]翟国华．几种常见涂色问题的一般解法[J] ．考试．高考数学，2007,31(05,06).