通过数学建模活动培养大学生综合能力的思考*
2014-08-03田兵
田 兵
(包头师范学院 《阴山学刊》编辑部,内蒙古 包头 014030)
数学是研究自然界数量关系和空间形式的科学,是其他学科发展的基础。它能够揭示在繁杂现象中所蕴含的客观规律,能够让我们更好的掌握这些客观规律来改善生活,能够让我们用严谨的逻辑和理性的思维来理解这个世界。
在当今社会,伴随着计算机日新月异的发展,数学从来没有像今天这样以前所未有的深度和广度在深刻地影响着各个学科、社会的各个领域以及生活的方方面面。其他学科的发展与成熟越来越依赖于数学的发展与应用。社会的各个领域和生活的方方面面在逐渐地被数学渗透和影响着。
在现实生活中我们所遇到的任何实际问题,最后都可以转化为相应的数学问题和数学模型,很多新设备、新技术的研制与开发都是在一定的数学模型指引下实现的。可以说人类是在通过不断的将实际问题抽象成相关的数学模型,又将数学模型应用到实际生活中的过程中向前发展。
1 数学建模的概念
对数学建模方法, 人们也有了比较统一的观点。将数学方法应用到任何一个实际问题中去, 首先是把这个问题的内在规律用数学、图表或公式、符号表示出来, 然后经过数学处理得到定量的结果, 以供人们作分析、预报、决策或建立控制, 这个过程就是通常所说的建立数学模型, 简称数学建模。
数学建模就是把现实世界的一个实际问题, 为了一个特定目的, 根据特有的内在规律, 做出一些必要的简化假设, 用适当的数学方法归结为数学问题, 建立起描述各相关量之间关系的数学式, 然后运用计算技术、计算机和相应软件在内的计算工具, 快速准确地计算出符合实际问题的解答。
数学建模的基本步骤包括模型准备、模型假设、构造模型、模型求解、模型分析、模型检验和模型应用。如图1所示
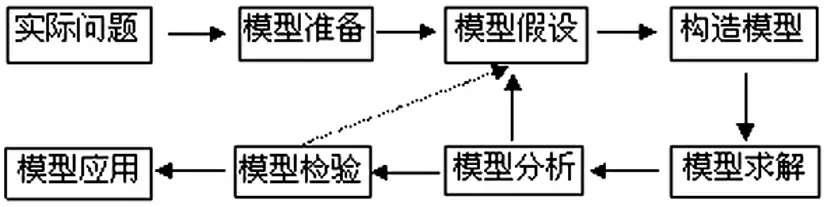
图1:数学建模的基本步骤
2 通过数学建模活动可以培养学生的综合能力
数学建模是对现实世界中所遇到的客观事物进行具体构造数学模型的过程。数学建模主要是通过对实际问题的抽象、简化、确定变量和参数, 并建立起变量和参数间的确定的数学问题,求解该数学问题。通过数学建模活动可以培养大学生的综合能力,有利于培养学生的自学能力、逻辑思维能力、创造能力、沟通能力和团队协作能力。
2.1 通过数学建模活动可以培养大学生的自学能力
在进行数学建模之前需要学生有丰富的知识储备,自学其他学科的内容。数学建模所要解决的问题大都来自工农业生产、经济、环境、生态、医疗、金融和保险等领域中的实际问题。这些问题有很强的实际背景,往往涉及多学科的知识。要解决这些问题学生们首先要对这些问题所涉及的某些学科有一定的了解。而在现有的教学体制下,学生的知识结构比较单一,他们往往只对自己所学的专业比较了解。而通过数学建模活动来解决这些实际问题,有助于激发学生们的学习兴趣,唤起他们的求知欲望,发挥他们的主观能动性积极地自学与所要研究的问题相关的其他学科的内容。
在进行数学建模之前需要学生自学计算机编程语言。计算机技术在二十世纪末得到了空前的发展。特别是在近几十年其计算的精度和智能程度上有了很大的提高。在此基础上开发的数学软件具备了强大的计算功能。现在的许多计算机软件不仅可以准确的计算线性方程和非线性方程的解,而且还可以求解非常复杂的数学模型,甚至可以完成对模型的检验和评价以及根据检验和评价结果对模型进行进一步的修正,最终得到问题的优化解。可以说计算机软件,是我们通过数学建模解决实际问题非常有效的工具。对于许多高校大学生来说,大都学习了C语言,但是对于数学建模来说,仅仅掌握C语言是远远不够的。如果想通过数学建模更快的解决实际问题,得到更加优良的解决方案,要求学生自学许多更加实用、运算速度更加快和针对性更强的计算机编程语言比如Matlab、Mathmatica、Maple等软件。
2.2 通过数学建模活动可以培养大学生的逻辑思维能力和创新能力
数学建模所解决的是一些非常实际的问题。这些实际问题里面隐藏着影响问题解决的因素和这些因素之间的联系。学生经过对这些复杂实际问题的认真分析后,首先从中找出影响问题解决的所有因素;结合实际问题的具体情况对所有因素进行判别,舍去次要的因素,保留最重要的因素;之后把这些最重要的因素抽象成变量,并且结合实际情况确定变量的变化区间;然后找出各个变量之间的关系,建立它们之间的函数关系,这个函数关系就是数学模型;最后通过计算机编程对所得到的数学模型进行模拟,对得到的数学模型进行评价、修正,找到最适合实际要求的数学模型。
数学建模的过程是一个创造性思维的过程。它要求学生认真审视所研究的问题,透过事物繁杂的现象找到影响事物发展最重要的因素之间的关系,并且用最简单的数学语言表现出这种关系。通过数学建模把一个非常复杂的实际问题抽象成简单的只包含一些变量的数学公式。
在整个数学建模的过程中学生经过观察、比较、分析、综合、抽象、概括、判断、推理,采用科学的逻辑方法,准确而有条理的表达自己的思维。在整个过程中学生都在积极的思考问题、解决问题,通过创新地应用自己已有的知识和所掌握的方法去解决未知的问题。在整个建模过程中学生发挥自己的想象力、洞察力、逻辑思维能力、创造力来解决实际问题。因此通过数学建模活动可以很好的培养学生的逻辑思维能力和创新能力
2.3 通过数学建模活动可以培养大学生的沟通能力和团队协作能力
需要解决的实际问题越来越复杂,单凭一个的力量是很难完成对实际问题的数学建模,这就需要多个人组成一个团队,互相影响,互相协调,互相帮助,发挥团队的力量、协同作战,最后共同完成建模任务。这样在整个建模过程中,需要每个队员有良好的人际沟通能力和团队协作能力。
参加数学建模活动有利于培养学生良好的人际沟通能力。沟通能力是学生顺利完成数学建模的必备能力。在建模过程中,首先要以积极地态度、用恰当的方式、准确的语言把自己对问题的看法和见解向自己的队友表达清楚,这样有助于队友更加全面而深入地了解自己的想法。其次,要善于认真的倾听队友的观点。这样一来是一方面给了队友表达自己意见的机会。另一方面使自己可以了解到别人的想法。每个人的想法都会有它可借鉴之处。“兼听则明,偏信则暗”。多听听其他人的见解可以使自己的想法更加成熟和完善。最后,要善于处理矛盾。一方面要善于处理自己与队友的矛盾和分歧。在向队友表达自己观点的时候,态度一定要诚恳,言语中不能带有高人一等和重伤、贬低他人的言辞。遇到自己的观点与队友的有分歧的时候,如果自己的想法是正确的一定要坚持己见,但是一定要耐心有理有据的向对方阐述清楚;如果别人的意见是正确的,一定要虚心接受,及时改正。另外一方面要善于处理队友与队友之间的分歧和矛盾。处理这样的矛盾,第一要摆正自己的心态,第二尽量倾听双方的意见,全面的了解双方的看法,第三做出正确的判断,以积极的态度与双方沟通,从而化解分歧,找到最好的解决方案。
参加数学建模活动有利于培养学生良好的团队协作能力。在建模之前,第一要了解每个队员的实际情况包括个人能力、性格特点和兴趣爱好;第二整理每个队员对整个建模的意见和看法,经过大家充分的讨论,最后形成切实可行的建模方案,第三明确每个队员在团队中的作用,根据每个人的实际情况,将整个建模工作合理的分派给每个队员;第四鼓励队员进行沟通,检查各自所承担的工作进展是否与整体计划协调,鼓励队员相互及时反馈,帮助解决合作中遇到的分歧和困难。
由于数学建模是一个艰苦的过程,其间面临着许多挑战, 因此通过参加数学建模活动, 有利于锻炼学生的毅力、意志;增强学生克服困难的信心、决心和勇气,同时培养学生团结合作精神和交流、表达的能力,提高组织协调能力。
3 结论
参加数学建模活动能促使学生涉猎更广泛的领域, 唤起学生求知的欲望,激发学生学习的热情和兴趣,促使学生不断地获取新知识、使用新方法和新技术,有利于培养学生的自学能力。通过参加数学建模活动既让学生体味到解决问题的快乐, 明白数学在现实世界中的作用, 又实现了数学教育的目的。
参加数学建模活动能可以促使学生面对复杂事物发挥想象力、洞察力、创造力和独立进行研究的能力, 培养学生的的逻辑思维能力和创新能力。
参加数学建模活动有助于提高大学生相互协作能力。在数学建模学习过程中,有大量的数学模型不是单靠数学知识就能解决的,它需要跨学科、跨专业的知识综合在一起才能解决,这就需要具有不同知识结构的人经常在一起相互讨论,从中受到启发。同学们在建模过程中彼此磋商、团结合作、互相交流思想、共同解决问题,使得知识结构互为补充,取长补短,从而提高了他们的沟通能力和团队协调能力。
〔参考文献〕
[1]杨启帆,边馥萍.数学模型[M].杭州:浙江大学出版社,1990.
[2]雷功炎.数学模型讲义[M].北京:北京大学出版社,1999.
[3]姜启源.数学建模[M].北京:高等教育出版社, 2005.
[4]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社,2005.
[5]孙宏安.数学模型法的三个来源[J].大连教育学院学报,1997.
[6]孙月蓬.关于数学建模的几点思考[J].北京邮电大学学报(社会科学版), 2001, 3(1).
[7]陈燕龙.开展数学建模推进素质教育的思考和设想[J].广州航海高等专科学校学报, 2001, 17(2).
[8]李医民,等.数学素质教育改革的系统工程[J].大学数学,2003,19(4):34- 37.
[9]刘二根.论数学建模[J].华东交通大学学报, 2004, 21(3).
[10]王茂芝,徐文皙,郭科.数学建模培训课程体系设计探讨[J].数学教育学报,2005, 14(1).
[11]李曦,肖文明,张蕾.以数学建模为载体的大学生素质教育的探究[J].教育学术,2009.
[12]王茂芝, 郭 科,徐文皙,周 游.数学建模中的创新意识培养[J].大学数学, 2009, 25(1).
