基于两次二维Daubechies小波变换的纸病在线辨识方法研究
2014-08-03杨雁南
周 强 张 慧 杨雁南
(陕西科技大学电气与信息工程学院,陕西西安,710021)
外观纸病是影响纸张外观、降低纸张质量的重要因素之一。因此,准确及时地在线检测纸病,并追溯严重纸病的病源(如机械故障带来的周期性纸病),对于优化生产过程、改善纸产品质量十分重要。
当前纸病的检测方法主要基于图像灰度特征实现,即利用高速摄像机拍摄纸张图像,然后用图像处理技术提取其灰度特征值进而辨识纸病,并用加标记、报警等方式来指导生产过程的实际操作。在这个过程中,照射纸面光源的不均匀对纸张图像的灰度特征提取影响很大,甚至改变纸病辨识结果。
常见的外观纸病包括黑斑、亮斑、空洞、油污、褶皱,考察的灰度特征值包括灰度均值、标准差和熵等。根据纸病灰度均值偏离正常纸张灰度分布的百分比来区分高对比度的纸病(如黑斑、亮斑)[1];利用灰度标准差可以辨别目标区域内灰度波动大的纸病(如孔洞、油污)。对于灰度分布特征不明显的纸病如褶皱,难以根据灰度特征来辨识[2]。有学者提出,利用Hough变换等方法来辨识褶皱,但是该方法仅适合于测量线形褶皱,且运算过程复杂,不易在线实现。也有研究提出,利用纸病图像的几何特征,即形态学方法,通过分析目标区域图像的周长、面积、矩形度、圆形度、分形维数等几何特征量辨识纸病[3],但由于褶皱纸病的边界十分模糊,加之背景及高频噪声的影响,导致这种纸病的几何特征难以提取,因此,这种方法的辨识效果不理想。
为克服外部光源的不均匀,本研究探讨了纸面图像背景补偿方法,同时在纸张褶皱灰度分布规律基础上,通过使用两次二维小波变换来实现在线辨识褶皱纸病。
1 纸病检测的硬件系统
本研究所用纸病在线检测系统如图1所示。由于纸面较宽(约2000 mm),在线形光源的照射下,使用2台DALSA公司Spyder 2高速数字摄像机对纸面进行线扫描,每台摄像机每行的扫描点数为2048点。纸张由里向外高速运动(最高速度4.5 m/s),纸速由光电编码器测量,并以编码器输出的速度脉冲作为高速摄像机的采样驱动信号,高速摄像机以0.5 mm的分辨率拍摄纸张图像。根据纸张灰度不同,由FPGA
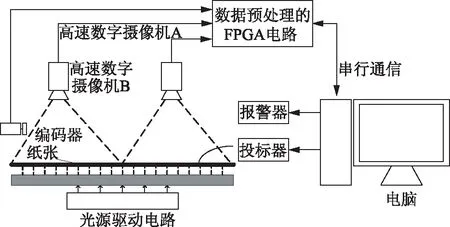
图1 纸病检测硬件系统框图
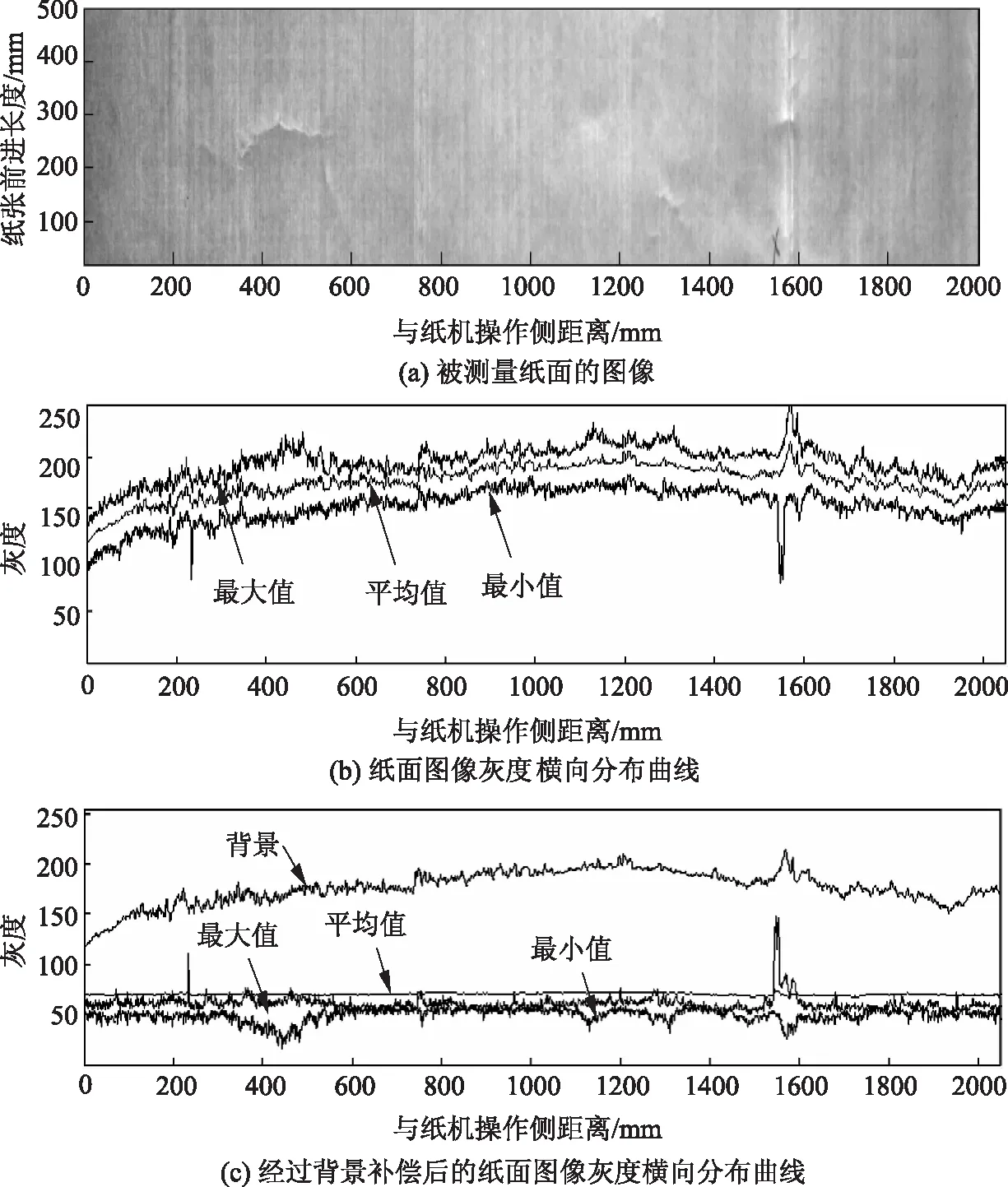
图2 光源分布的不均匀性问题及图像灰度动态补偿
的数据采集和预处理电路初步判断出纸面上纸病区域,确定区域位置和大小并保留该区域的灰度,将这些数据以串行通信上传至计算机。该电路的使用分担了计算机的部分任务,从而缓解了纸病检测数据量大的瓶颈问题,计算机处理上传数据,实现对纸病区域的纸病辨识。根据辨识结果控制投标器对纸病处加标记,如果出现重大纸病(如周期性纸病),报警提醒操作人员,以便及时补救。
2 纸面背景灰度动态补偿问题的研究
由于高速摄像机扫描为线形区域,照射光源选用线形LED光源,从而避免了光线衍射和光源频闪等问题,但线形光源存在光强度不均匀问题,如高速摄像机拍摄的纸面图像(见图2(a))。图2(b)为纸面图像灰度的横向分布。由此可以看到,灰度一方面存在着随机波动,即噪声信号;另一方面,表现出明显的两端灰度小、中间灰度大的灰度分布不均匀现象,这是由于线形光源光强度不均匀造成的。这个问题给纸病检测带来困难,如纸面两端的灰度已经接近纸面坐标(220,360)和(1550,450)处的灰度。纸病引起的横向灰度最小值曲线的灰度谷值使得纸病灰度阈值的选择范围变得很小。
为此,需要对纸面图像进行补偿。实时记录纸病背景图像的灰度并计算其横向分布平均值,进而获得图2(c)中的背景补偿后纸面图像灰度横向分布曲线。由于没有纸病,其灰度较高,又因为用于平均的数据(行数)较少,其波动较大,以行矩阵的形式将背景曲线记为background(是一个1×2048矩阵),background分别减去灰度分布最大值矩阵Max0、最小值矩阵Min0和均值矩阵Mean0:
Max=background-Min0
(1)
Min=background-Max0
(2)
Mean=background-Mean0
(3)
获得新的Max、Min和Mean(见图2(c))。背景补偿后,Max、Min和Mean变得平直,弥补外界光源所造成的背景图像灰度分布不均匀问题。由此可见,纸面中纸病对应的灰度峰值、谷值显得很突出,给下一步的特征提取和模式识别带来了方便。实际中使用的补偿公式为:
a(u,v)=B(u,v)-f(u,v)
(4)
式中,u、v分别为纸病图像平面坐标横向、纵向的离散化变量(1≤u≤2048,1≤v≤480),f(u,v)是摄像机每次扫描纸张表面的一行所得到的灰度矩阵(一个1×2048矩阵)。考虑到背景曲线经滤波后还有一些噪声成分,同时外界环境(包括光强度、纸面亮度和平滑度等)的变化会引起背景曲线发生变化。为此,在实际补偿中,需要根据背景灰度建立补偿曲线的趋势项矩阵B(u,v)的函数b(u,v)。
b(u,v)=bN(v)uN+bN-1(v)uN-1+…+b0=
(5)
检测过程中,实时辨识背景图像的灰度变化调整模型参数{bn,n=0,1, … ,N},以实现对光照强度和环境变化的动态补偿。连续的480个行矩阵a(u,v)构成了一幅纸面的图像A(u,v)(480×2048的灰度矩阵),进行纸病检测。
模型参数{bn,n=0,1, … ,N}的实时辨识方法为:当高速摄像机扫描到纸张表面的第m(v=m)行时,在该行的2048个像素点上,等间距选取N个点,这些点的灰度分别为b(u1,m)、b(u2,m)、…、b(uN,m),代入公式(5),则有:
(6)
进而得到:
(7)
由上述公式可计算出每列的模型参数{bn,n=0,1, … ,N}。由于{bn,n=0,1, … ,N}的变化是随外界环境光线而变化的,其变化速度较慢,因此,每隔10 min左右自动辨识1次即可。
3 纸病检测方法
3.1 纸病灰度的数值特征
生产过程中,常见的纸病有黑斑、亮斑、褶皱(或划痕)、孔洞、边缘裂缝等。实验分析表明,黑斑、亮斑和孔洞的灰度和背景灰度有较大差别,黑斑灰度低于背景灰度,亮斑灰度高于背景灰度,孔洞灰度根据使用光源的不同与背景灰度有明显差异。在使用前光源和背光源的情况下,孔洞纸病部分的灰度分别低于和高于背景灰度[4]。
图3(a)中的图像含有黑线、黑斑、孔洞等纸病;图3(b)是该图像灰度的横向分布曲线;图3(c)是经过背景动态补偿后的图像灰度横向分布曲线。由此可见,这些纸病的灰度与背景灰度有明显差异,使用适合的阈值能够很容易地辨识这些纸病。目前,很多检测方法都可以准确地检测出这些纸病。
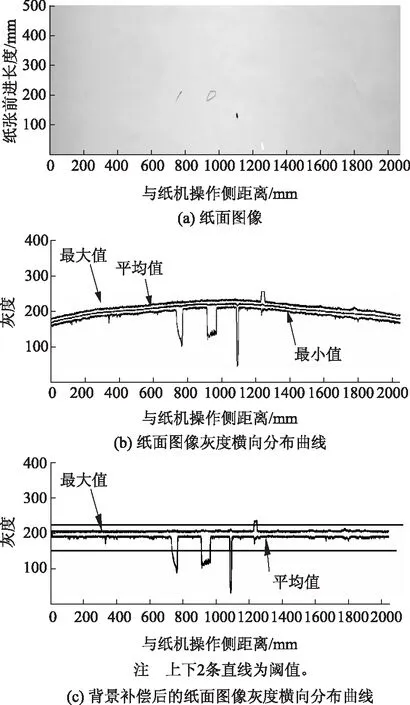
图3 主要纸病灰度的数字特征
褶皱纸病是由于纸张在运行过程受到的张力不均匀和本身收缩不一致造成的。这种纸病的灰度与背景灰度大体相当,因而难以辨别。图4给出了褶皱纸病及其灰度水平和垂直方向的图像分布曲线。由图4可知,图像灰度含有较强的噪声,同时,因背景不均匀带来的水平方向灰度曲线趋于单调下降。此外,在空间域内难以发现其他明显特征。因此,本研究尝试在空-频域使用二维小波变换寻找其灰度特征规律。
3.2 基于二维小波变换的褶皱辨识
二维小波变换是一维小波变换在二维空间的拓展, 连续二维小波变换形式为[5- 6]:

(8)
式中,ax、ay、bx、by分别是x、y方向的尺度和位移变量。A(x,y)是被分析的连续二维变量,由于待分析的图像A(u,v)是以整数矩阵形式表示,则A(u,v)的二维小波分析工具是离散的,表达式为[7]:
(9)
根据一般褶皱纸病灰度的频谱宽度及奇异程度,使用离散二维小波分解图像矩阵A(u,v)到二层,其算式为:
(10)
式(10)中的小波函数可以展开为:
φ(u,v,j)=Φj(u)Φj(v)+Φj(u)ψj(v)+
ψj(u)Φj(v)+ψj(u)ψj(v)
(11)
式中,Φj(·)和ψj(·)分别是二维尺度函数和小波函数,它们是通过对一维小波尺度函数和小波函数的张量积变换得到的。纸面图像经过二维小波分析,获得一系列不同尺度的子图像;大尺度图像分辨率低,但可以获得纸面的轮廓信息[8];小尺度图像分辨率高,能够提取纸面的细节或吸收图像中的噪声成分。j层的小波分解将分析对象A(u,v)分解为4个部分。
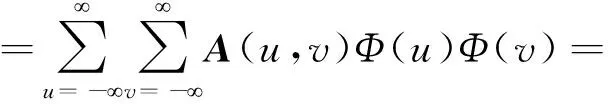
(12)
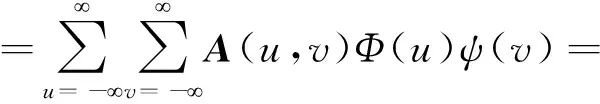
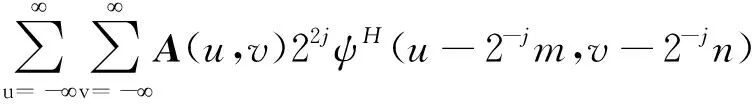
(13)
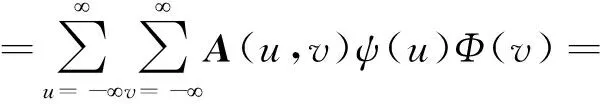

(14)
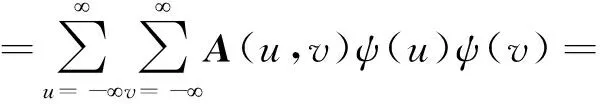

(15)
式中,DAj(m,n)、CHj(m,n)、CVj(m,n)、CDj(m,n)分别为纵横向均为低频(2j尺度)、纵向低频(2j尺度)横向高频(2j+1尺度)、纵向高频(2j+1尺度)横向低频(2j尺度)以及纵横向均为高频(2j尺度或2j+1尺度)的小波变换。
《语林》云:“陆士衡为河北都督,已被间构,内怀忧懑,闻众军警角,谓其司马孙掾曰:‘我今闻此,不如华亭鹤鸣也。’”[注] (唐)虞世南辑录《北堂书钞》卷一百二十一《武功部九·角二十九》,北京:学苑出版社,2015年,下册,第269页上栏。标点为本文所加,下同。

图4 褶皱纸病及其灰度分布图
本研究根据褶皱的灰度分布规律,采用两次二维小波变换:第一次小波变换分离图像背景噪声、提取小波轮廓,第二次小波变换增强、提取轮廓的特征信息。
(1)第一次使用二维小波变换处理纸面图像
褶皱纸病的图像虽然在灰度上很难找到特别突出的全局最大值和最小值(峰值和谷值),但是在折线两侧(以折线为分界线)往往一面暗一面亮形成2个灰度区域,形成1个灰度的阶梯,这个规律在图3中有时可以看到。图3(a)中在纸面坐标(1790,250)处有一个较小的褶皱,其对应的图3(b)中横坐标1790上方的最大值曲线的小块突起是由于纸张褶皱处“亮面”造成的;同样,最小值曲线的小块凹陷是由于纸张褶皱处“暗面”引起的。图3的纸面比较干净,灰度分布曲线较为平滑,因此,这个规律较为突出。图4中的纸面褶皱更大,而且,从图4的(b)和(c)的灰度分布曲线看不出上述规律。这是由于图4的纸面粗糙,灰度噪声信号幅度较大,淹没了褶皱所引起的灰度“阶梯”。为了消除噪声影响,提取褶皱带来的灰度轮廓,本研究第一次使用二维Daubechies小波(尺度系数为4的Daubechies小波,记为DB4)来处理纸面。

图5 纸面图像灰度的Daubechies二维小波变换
由于在已有的小波基中, Daubechies小波是一组正交小波, 具有良好的检测突变信号的能力,常被用于检测边缘和图像增强。本研究利用它来完成消除灰度噪声、增强褶皱轮廓的作用。由于主要使用低频信息,小波分解到二层。图5的(a)和(b)分别是纸面图像的二维低频DB4小波DA2(m,n)和横向高频DB4小波CH2(m,n)的图像。
显然,二维DB4小波的高频部分吸收了大量噪声成分,使得低频部分出现明显的阶梯状,这正是褶皱纸病引起的。为了进一步突出纸病特征,对DB4的低频小波DA2(m,n)进行一次二维小波变换。
(2)第二次使用Haar二维小波处理DB4的低频部分
第二次使用小波的目的是为了增强褶皱纸病灰度的分布特征,便于特征提取。由于Haar小波(尺度系数为1的Daubechies小波)在某一点处呈阶跃状,与被分析对象有一定相似性,因此,使用Haar小波来实现二维分析。Haar小波的小波函数为:
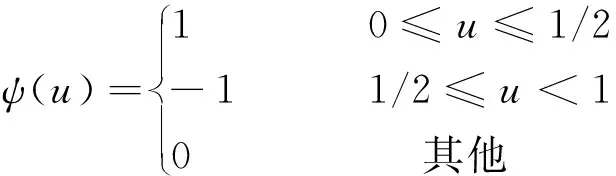
(16)

(17)
纸面灰度二次低频小波DA2(m,n)的二维Haar小波的低频部分和高频横向分别是:
(18)
(19)
DAk(p,q)和CHk(p,q)的三维图如图6所示。
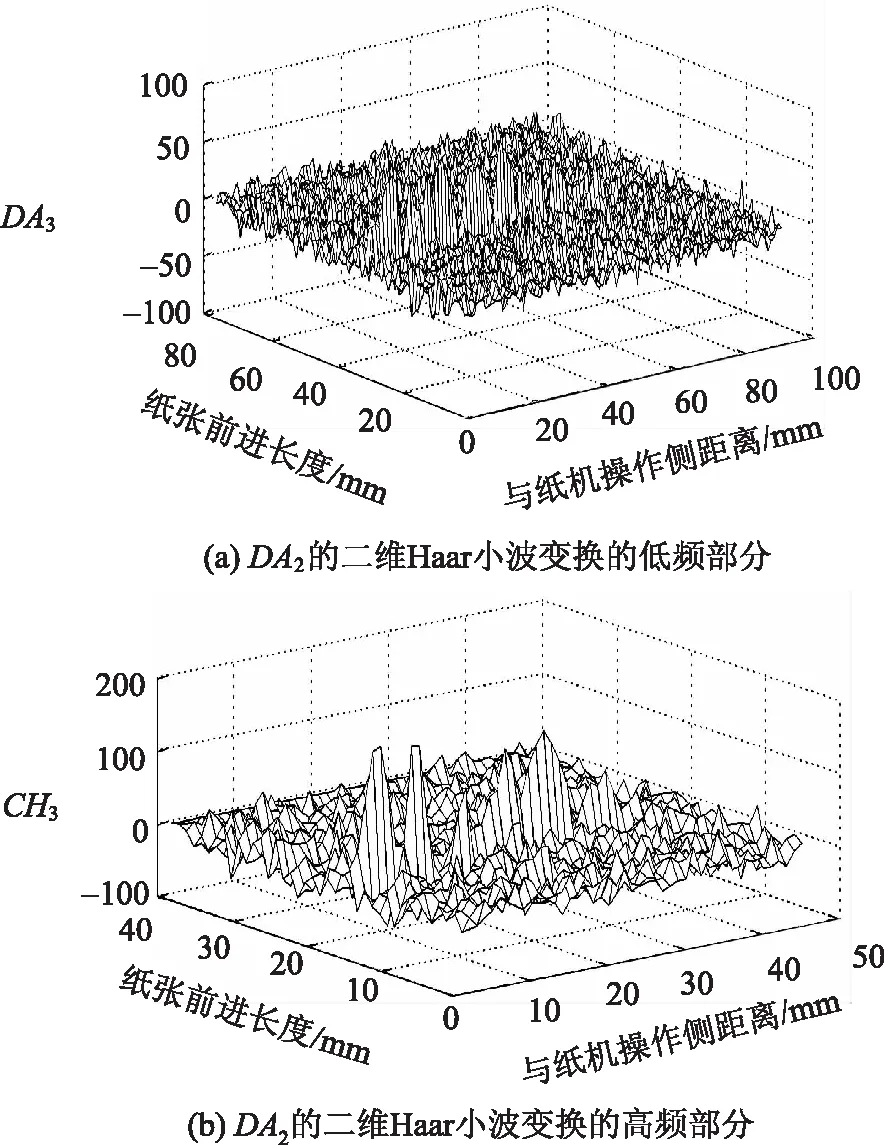
图6 纸面灰度的DB4小波低频部分的二维Haar小波变换
通过对纸面灰度DB4小波低频部分的Haar二维小波变换,获得其低频和高频部分。由图6可见,在纸面褶皱处出现了显著的峰值,其中,高频部分的峰值更为突出。因此,对DHk(p,q)进行二值化处理,图像灰度阈值设为80(或其他,因为图中峰值突出,阈值可取值范围很宽):
(20)

图7 二值化处理后的褶皱特征提取
图7是二值化后Sgn(p,q)的平面图形。图7中呈现一条明显的锋线,根据阈值锋线的连续情况不同,只要有超过阈值的二次小波系数DHk(p,q)出现,就能够判断有褶皱纸病出现,而锋线的长度可以用于定量描述褶皱纸病的大小。
(21)
公式(21)中的2k是用于补偿由于尺度减小带来的距离误差。
3.3 纸病处理流程
完整的图像纸病检测流程为:首先收集一行图像数据,然后根据纸病背景图像的数学模型对光源造成的不均匀性进行动态补偿,使480行数据构成一幅图像,对此图像矩阵进行第一次小波变换,去除高频部分,即噪声部分,保留低频部分,即有效信息部分,然后对纸病区域进行第二次小波变换,保留特征更加明显的高频部分,判断出各种纸病(包括难点纸病,如褶皱)的类型。具体的纸病检测流程如图8所示。
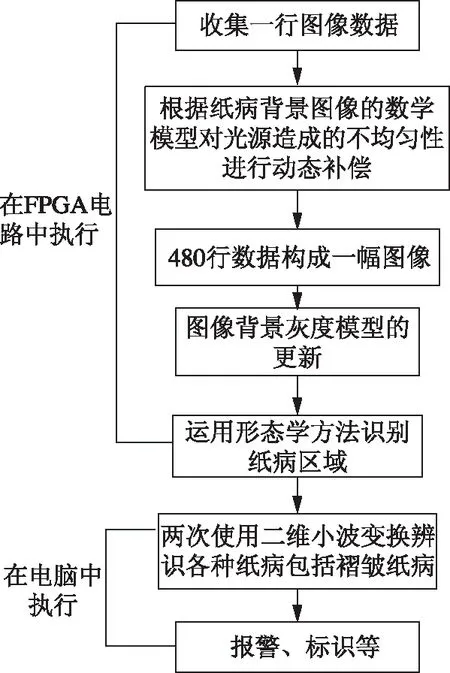
图8 纸病检测流程图
3.4 其他纸病辨识对于褶皱纸病辨识的影响
在造纸生产中,常常发生多种纸病同时出现在一幅纸张图像的情况。当黑线、黑斑、孔洞在小波变换中属于突变信号与褶皱纸病同在一幅图像上,本研究探讨了检测褶皱纸病是否会受到影响。研究表明,由于小波变换对空-频域奇异、非线性信号具有多分辨分析能力,因此,本研究提出的方法对其他纸病的检测同样有效,而检测过程中不会发生多种纸病间的相互影响。
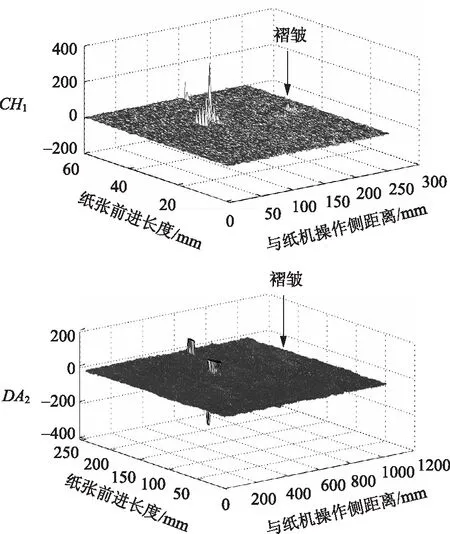
图9 图3(a)的两次二维小波变换
以图3(a)为例,该图的右侧存在一个不明显褶皱(该褶皱算不上一个纸病),对该图的两次二维小波变换结果如图9所示。由图9可见,虽然这个褶皱不明显,在两次小波的不同频段对其都有反应,经过第一次小波变换,取高频,基本能够辨识出纸病,为了突出不同纸病的特点,进行第二次小波变换,取低频。这表明该方法能够测量褶皱以外的其他纸病。
4 结 语
本研究探讨了在线纸病检测系统光源不均匀的问题和褶皱纸病的辨识方法。通过建立纸面图像背景灰度的数学模型,利用模型实施光源不均匀性的动态补偿。经过两次二维小波变换能够有效在线辨识包含难点纸病(褶皱)在内的各种纸病类型,分辨率可以达到0.5 mm。
参 考 文 献
[1] MONICA Benito, DANIEL Pena. Detecting defects with image data[J]. Computational Statistics & Data Analysis, 2007, 51: 6395.
[2] ANZAR Alam, JAN Thim, MATTIAS O′Nils, et al. Online surface characterization of paper and paperboards in a wide-rang of the spatial wavelength spectrum[J]. Applied Surface Science, 2012, 136(4): 7928.
[3] Shanmugavadivu P, Sivakumar V. Fractal dimension based texture analysis of digital images[C]//Procedia Engineering, 2012, 38: 2981.
[4] 杨 波, 周 强, 张刚强. 基于几何及灰度特征的纸病检测算法研究[J]. 中国造纸, 2011, 30(9): 52.
[5] Huang Yi, Meyer D , Nemat-Nasser S. Damage detection with spatially distributed 2D Continuous Wavelet Transform[J]. Mechanics of Materials, 2009, 41 : 1096.
[6] Niu H, Quan C, Tay C J. Phase retrieval of speckle fringe pattern with carriers using 2D wavelet transform[J]. Optics and Lasers in Engineering, 2009, 47: 13349.
[7] Zahouani H, Mezghani S, Vargiolu R, et al. Identification of manufacturing signature by 2D wavelet decomposition[J]. Wear, 2008, 264: 480.
[8] Thulasiraman Parimala, Khokhar Ashfaq A, Heber Gerd, et al. A fine-grain load-adaptive algorithm of the 2D discrete wavelet transform for multithreaded architectures[J]. Journal of Parallel and Distributed Computing, 2004, 64 (1): 68.
