基于形态滤波和HHT的滚动轴承故障特征提取
2014-08-02刘继承聂品磊杨宏宇宋剑白杨文涛
刘继承 聂品磊 杨宏宇 宋剑白 杨文涛
(东北石油大学电气信息工程学院,黑龙江 大庆 163318)
旋转机械广泛应用于许多重要工程领域,如电力、化工、冶金及机械制造等。而在此类领域中旋转机械设备往往是关键设备,其运行状态的好坏直接或间接地影响着国民经济生产。滚动轴承是旋转机械中极为重要的部件,如果能够对其工作时产生的振动信号加以处理,并从中提取出其故障参数、发现其潜在故障,必将降低此类机械的检修率、提高其运行效率、保证其工作稳定性,进而为国民经济生产做出贡献。而能否准确地从复杂的振动信号中提取出故障参数就成了至关重要的问题。实际上,当滚动轴承有故障发生时,其振动信号各频带的能量将发生变化,因为丰富的故障信息必将蕴含在各频带信号的能量中[1]。
目前,提取振动信号故障特征的主要技术方法有:小波变换(WT)、现代谱分析、主元分析(PCA)、独立分量分析(ICA)、高阶统计量分析和被引入旋转机械故障诊断领域的混沌与分形动力系统理论[2]。1998年,Huang N E等提出了HHT方法,在该方法中,首先对信号进行经验模态分解(EMD),之后对内模函数(IMF)做Hilbert变换,以获得信号的瞬时频率等信号特征[3]。对于非平稳、非线性信号,使用HHT方法提取其故障特征具有很大的优势,但如果信号中混有大量噪声,在EMD分解时会产生模态裂解现象,使信号频谱中出现较多虚假频率。对此笔者使用形态滤波对故障信号进行降噪处理,以减小EMD的模态裂解现象,提高故障特征提取的准确度。首先阐述了用于信号预处理的形态滤波算法、HHT算法的基本原理和滚动轴承故障频率的计算方法;之后采用美国凯斯西储大学(Case Western Reserve University,CWRU)滚动轴承数据中心提供的振动信号进行实验以验证本算法,并与故障信号的FFT谱进行对比。
1 算法简介①
1.1 形态滤波
用EMD方法分解混有噪声的信号时之所以产生模态裂解现象,其中一个很重要的原因是噪声严重干扰了极值点,以至于极值点在整个采样时间内分布不均匀。如果能够采用合理的降噪方法对信号进行降噪,必将有效地减小EMD分解时的模态裂解现象,提高故障特征提取的准确度。使用数学形态学方法对信号波形进行的研究完全在时域中进行,在处理过程中只有信号的局部特征起作用,波形在处理后不存在相移及幅值衰减等问题;而且数学形态学只包含加、减法和取极值运算,不涉及乘、除法。与传统的降噪处理方法相比,数学形态学具有诸如计算简单、实用性好及时延较小等优点。在振动信号降噪处理方面,它是一种新的、高效的降噪方法。
数学形态学由4种基本运算组成:腐蚀、膨胀、开运算和闭运算[4]。
假设输入序列f(n)为定义在Df=(0,1,2,…,N-1)上的离散函数,序列结构元素g(n)为定义在Dg=(0,1,2,…,M-1)上的离散函数,且N≥M,则f(n)关于g(n)的膨胀和腐蚀为:
(f⊕g)(n)=max[f(n-m)+g(m)]m∈0,1,2,…,M-1
(fΘg)(n)=min[f(n+m)-g(m)]m∈0,1,2,…,M-1
(1)
其中,⊕为膨胀运算;Θ为腐蚀运算。(n-m)∈Df且m∈Dg;(n+m)∈Df且m∈Dg。
在数学形态学中,膨胀和腐蚀两种基本运算经过组合可以得到具有滤波性质的另外两种基本运算:开运算和闭运算。一些结构比较复杂的形态滤波器通常由开运算和闭运算构成。f(n)关于g(n)的开运算和闭运算分别为:
(f∘g)(n)=(fΘg⊕g)(n)
(f·g)(n)=(f⊕gΘg)(n)
(2)
通过对形态学开、闭运算进行级联,Maragos构造了一种新的滤波器,其可以同时去除信号中的正、负脉冲两种噪声,即形态开-闭FOC和闭-开FCO滤波器,分别定义为[5]:
FOC(f(f))=(f∘g·g)(n)
FCO(f(n))=(f·g∘g)(n)
(3)
笔者所使用的组合滤波器是将上述形态学开-闭滤波器和闭-开滤波器进行组合形成的一种平均组合形式的滤波器,能够对信号中的各种噪声成分进行有效抑制,其输出信号y(n)为[6]:
y(n)=[FOC(f(n))+FCO(f(n))]/2
(4)
影响形态滤波器性能的主要原因是形态学运算中的结构元素。形态学滤波效果的好坏很大程度上取决于结构元素的形状和尺寸,在选取结构元素时,要尽量使结构元素的形状和尺寸与所处理信号相匹配,这样可以提高信号的滤波效果。常见的结构元素有直线型、三角型、正弦型及椭圆型等。
笔者采用结构元素为三角型的组合形态滤波器。原振动信号与去噪后的振动信号如图1所示。由图1可看出,通过形态组合滤波,信号中的噪声明显减少。上述结果说明形态组合滤波能有效地减小噪声干扰,通过形态组合滤波对信号进行降噪处理是可行的。
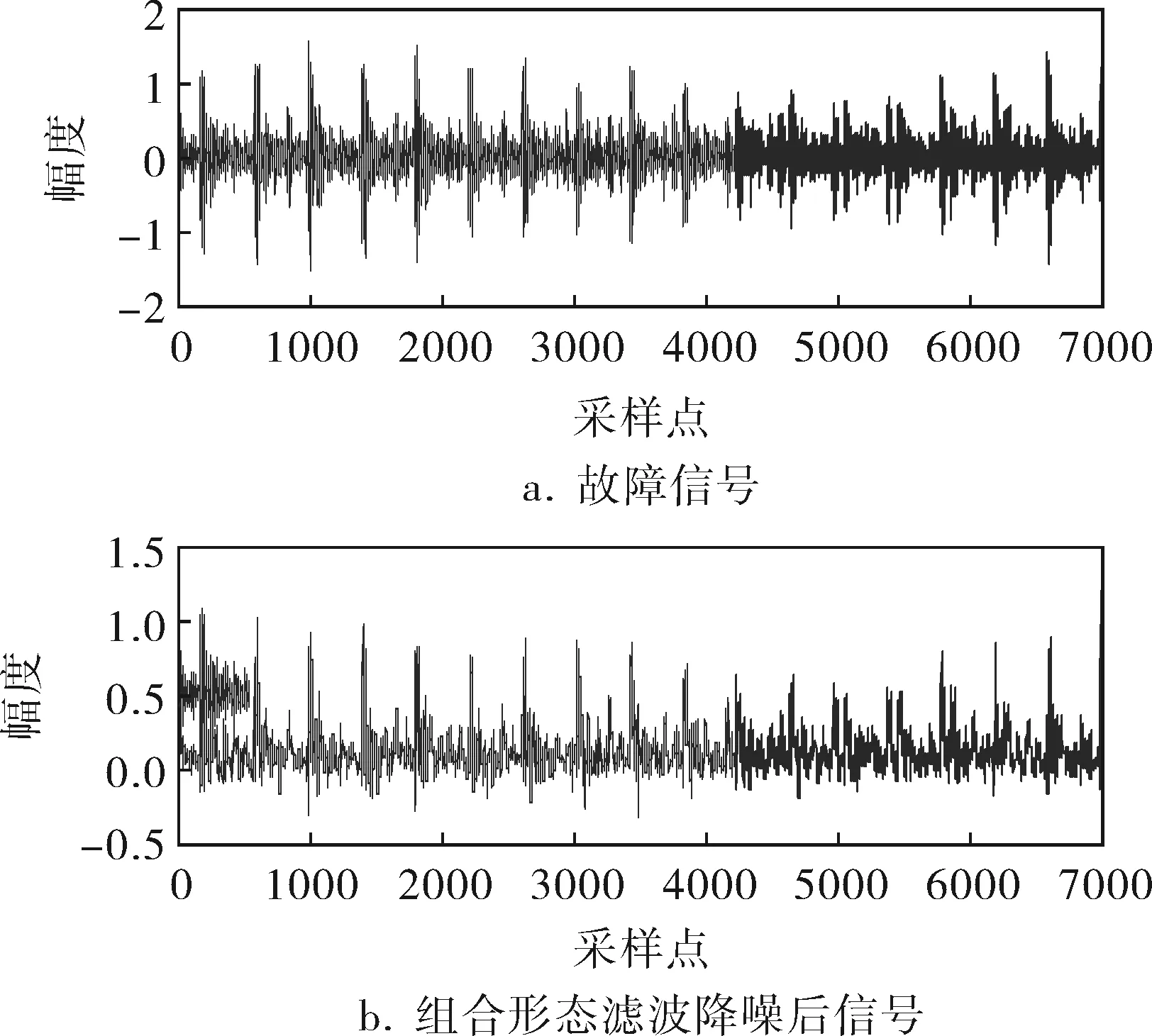
图1 故障信号与形态滤波后的信号
1.2 基于形态滤波和HHT的信号特征频率提取
在瞬时频率概念的基础上,Huang N E 等于1998年提出了基于EMD的时频分析方法。经验模态分解方法的本质是通过对信号进行平稳化处理,逐级分解出一系列具有不同特征尺度的数据序列,这将有利于对信号进行进一步处理[7]。
经验模态分解的基本思路可以概括为:第一步,采用三次样条插值函数循序连接待分析数据序列x(t)的所有极大值点,得到x(t)的上包络线,同理可得到其下包络线;之后计算上、下包络线的均值,记为Mx(t);原始数据序列中减去包络均值Mx(t)可得到一个新的数据序列h1(t),即h1(t)=x(t)-Mx(t)。但此时h1(t)一般无法满足平稳数据序列的要求,需对h1(t)重复上述过程。记h1(t)的包络平均为Mh1(t),数据序列h2(t)为去除该包络平均Mh1(t)所代表的低频成分后的数据序列,即h2(t)=h1(t)-Mh1(t),如此重复上述过程i次后,若Mhi(t)→0,这时得到的波形已经是严格局部对称的波形,hi(t)即为第一个内模函数(IMF)分量,记为c1(t),其也是信号数据序列中频率最高的成分。第二步,从x(t)中减去c1(t),得到一个新数据序列r1(t),此时r1(t)已被去掉一个高频成分。使用第一步中的方法,对r1(t)再进行分解,可计算出第二个内模函数分量c2(t)。同理,重复上述过程,直到数据序列rn(t)不能够被再一次分解,此时rn(t)不是内模函数,而是代表数据序列x(t)的趋势或均值。
在EMD算法中,一阶导数为零的点即为极值点,通过上述过程,最终信号可表示为:
(5)
为验证EMD方法的合理性和有效性,分析仿真信号:
y=cos(2πf1t)+10cos(2πf2t)
(6)
其中f1=10Hz,f2=50Hz。用EMD方法对仿真信号进行分解,结果如图2所示。

图2 仿真信号及其各IMF分量
图2中,第一个IMF分量对应着频率为50Hz的余弦信号,第二个IMF分量对应着频率为10Hz的余弦信号,残余量res表现为单调函数。通过对仿真信号的处理不难看出,EMD方法确实合理、有效,但同时也存在不足,从图2中可以看出,EMD分解的结果中出现了imf3这一并不存在的频率分量;此外,由于EMD采用了3次样条插值函数,imf1、imf2并不是原始信号的真实波形,所以才会出现代表信号波动趋势的残余分量res。
在EMD分解后,分别对得到的每个IMF做Hilbert变换,可得Hilbert谱,记作:
(7)
由此可以定义Hilbert边际谱为:
(8)
则Hilbert边际能量谱可定义为:
(9)
对式(6)中的模拟信号相应IMF边际谱求和,得到模拟信号的希尔伯特能量谱(图3),从图3中可以看出本算法能够准确提取出模拟信号中包含的两个频率分量,即50、10Hz。

图3 模拟仿真信号的希尔伯特能量谱
2 滚动轴承振动信号故障特征提取
根据滚动轴承的运动分析,Balderston于1969年得出滚动轴承的故障频率计算公式。轴承在对应转速下的故障特征频率为故障频率乘以相应的转速频率。
式中d——滚动体直径;
D——轴承节径;
f0——转轴旋转频率;
n——滚动体数目;
θ——接触角(推力轴承接触角θ=90°)。
笔者所用的实验数据来源于美国凯斯西储大学滚动轴承数据中心。文中所用数据为植入内环故障的滚动轴承振动加速度信号,电机转速为1 797r/min,采样频率为12kHz,轴承型号为6205-2RS JEM SKF型深沟轴承。轴承尺寸数据如下:
内径 25mm
外径 51mm
厚度 15mm
滚动体直径 8mm
节圆直径 39mm
由此计算出实验中使用的滚动轴承内圈故障频率约为162Hz。实验中使用的故障信号如图4所示,其EMD分解结果如图5所示。通过笔者所用的方法计算出的希尔伯特能量谱如图6所示,其中160.3Hz为振动信号的故障特征频率,这一结果与信号的故障特征频率理论计算值非常接近;同时能量谱中还存在滚动轴承的转动频率28.1Hz及其高次谐波188.6Hz,其值也非常接近滚动轴承的转动频率29.9Hz。通过与图7中的FFT谱相对比可以明显看出,根据笔者所采用的方法得到的故障频率准确率较高。

图4 原故障信号

图5 振动信号EMD分解结果

图6 故障信号希尔伯特能量谱

图7 故障信号的FFT谱
3 结束语
笔者提出形态滤波与HHT相结合的方法提取滚动轴承的故障频率,实验结果说明该方法切实有效。采用形态滤波方法对信号去噪能减小EMD分解时的模态裂解现象,提高故障特征提取的准确度;HHT方法的使用,使故障频率提取方法更适合于非线性、非平稳的滚动轴承振动信号。采用其他方法进一步减小EMD中的模态裂解现象,提高故障频率提取的精度是后续的研究方向。
