基于三级多源信息融合结构的SINS性能测试综合评估算法

李军伟，程咏梅，陈克喆

（1.西北工业大学 自动化学院，西安 710072；2.河南大学 计算机与信息工程学院，开封 475004）

基于三级多源信息融合结构的SINS性能测试综合评估算法

李军伟1,2，程咏梅1，陈克喆1

（1.西北工业大学 自动化学院，西安 710072；2.河南大学 计算机与信息工程学院，开封 475004）

针对 SINS性能测试存在指标多、不确定性等问题，提出了一种基于三级多源信息融合结构的SINS性能测试综合评估算法。给出了包括精度测试、稳定性测试和可靠性测试等三大性能测试指标和16个性能测试底层子指标构成的SINS性能测试指标体系，并构建SINS测试评估结构框架。利用多个专家对底层性能测试子指标进行评估给出相应性能子指标的模糊评价，并构造基本置信指派组成多个证据；利用基于局部冲突分配的组合规则进行三级证据融合，得到性能测试指标的综合评价结果。仿真实验结果表明：与传统的证据理论融合方法相比，该算法可以较为全面地很好地评估SINS性能，而且结果更为合理。

捷联惯性导航系统；性能评估；专家系统；模糊评判；信息融合

捷联惯性导航系统(Strap-down Inertial Navigation System，SINS)从研究、设计、制造、存储到实用的各个阶段，都需要对SINS进行一系列的性能测试[1-5]，包括仿真实验和物理试验，以确保它们在工作中具有的性能和品质，从而积累大量的测试数据信息，如何充分利用这些获得的信息对SINS性能进行综合评估，是SINS性能测试工作中的一个关键问题。

在SINS性能测试中，由于SINS受到仪器精度和环境干扰等因素的影响，单一性能测试评价指标对SINS性能进行测试评估是不可靠的，因此，使用多个SINS性能测试指标可以对SINS性能进行更全面、更为准确的评估。而证据理论(Dempster-Shafer Theory,DST)作为一种处理不确定性的推理方法[6]，可以处理存在不确定因素的评估。

本文首先建立了 SINS性能测试指标体系，该体系由 SINS的精度测试、稳定性测试和可靠性测试等三大性能测试指标和16个SINS性能测试底层子指标构成，提出了一种基于三级多源信息融合结构的SINS性能测试综合评估算法。由多个专家根据每个 SINS性能测试底层子指标对 SINS性能测试子指标给出性能测试评估的模糊评判，然后利用基于焦元距离的局部冲突分配DST(Local Conflict Distribution Based on the Focal Element Distance，LCD-DST)组合规则[7]对多个专家意见进行融合，再将多个性能测试子指标的专家融合意见进行逐级融合得到 SINS性能测试评估结果，最后，通过算例对提出的算法性能进行了验证。

1 SINS性能测试指标体系

在SINS性能测试评估中，如何合理选择评估指标和相应的评估方法，是系统性能测试评估总体设计时首要考虑的问题。本章建立由精度测试、稳定性测试和可靠性测试等构成SINS性能测试分析的一个呈树状的SINS性能测试指标体系，SINS性能测试指标体系如图1所示。

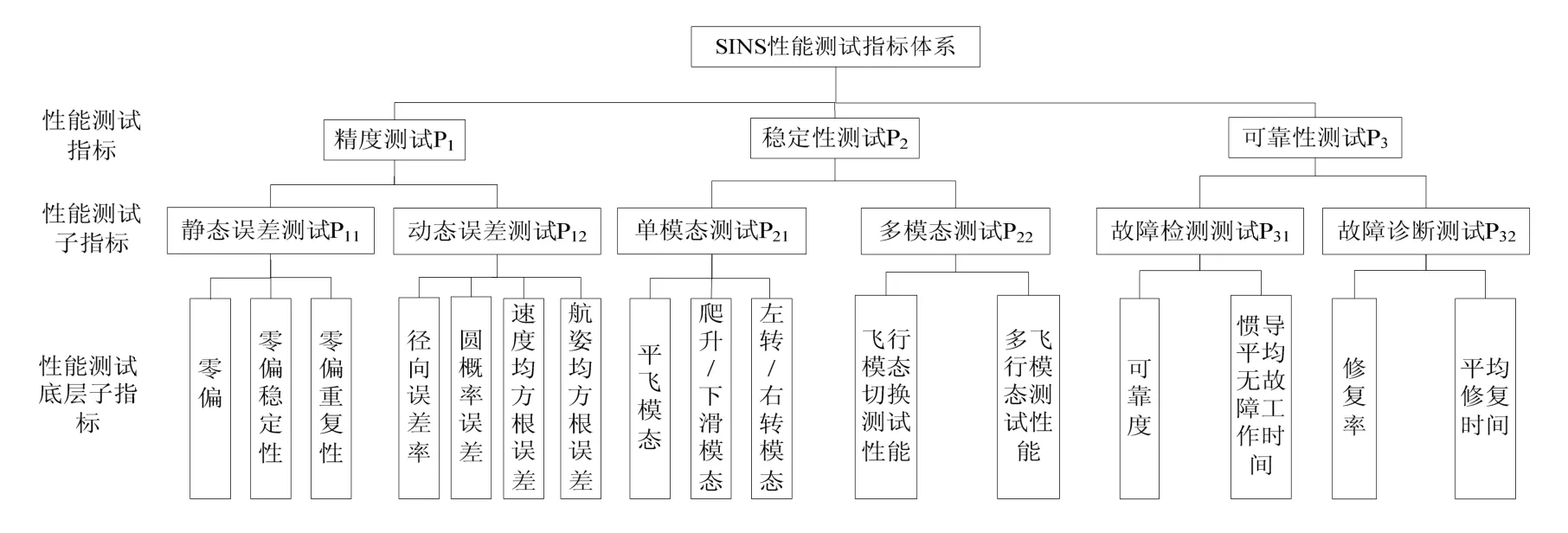
图1 SINS性能测试指标体系Fig.1 The index system of the SINS performance test

SINS性能测试评估指标体系中的精度测试包括静态误差测试和动态误差测试，稳定性和可靠性的测试主要包括飞行模态测试和故障检测测试和诊断测试，以此反映对SINS的检测能力和容错能力。

1.1 精度测试

SINS精度测试分为静态误差测试和动态误差测试。SINS静态误差测试性能测试指标主要包括零偏(Bias,B0)、零偏稳定性(Bias stability,Bs)和零偏重复性(Bias repeatability,Br)等[4]。

1）零偏

零偏指陀螺仪在输入角速率为零时的陀螺仪输出量：

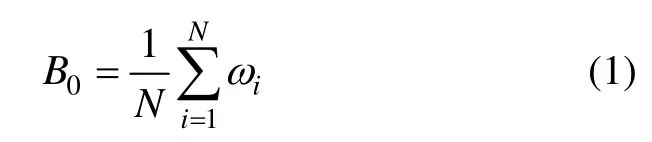
式中，N为采样次数；B0为零偏，单位为(°)/s；iω为陀螺仪的输出量，单位为(°)/s。

2）零偏稳定性

零偏稳定性以陀螺仪一定时间内的输出量的标准偏差相应的等效输入角速率表示：

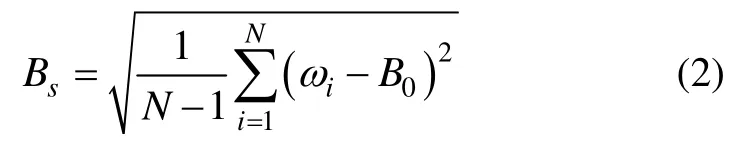
式中，Bs为零偏稳定性，单位为(°)/s。

3）零偏重复性

零偏重复性在相同的条件及规定的时间间隔内进行重复测量时输出陀螺仪零偏之间的一致程度，以各次测量所得零偏的标准差表示：

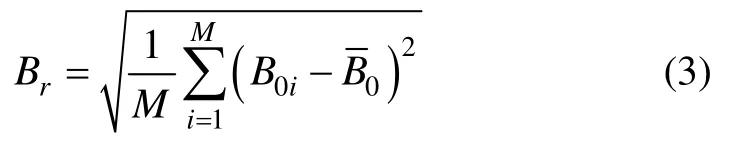
式中，M为重复测量的次数；Br为零偏重复性，单位为(°)/s；B0i为第i次测试的零偏；为M次测量所得到的零偏均值。

加速度计零偏、零偏稳定性及零偏重复性测试与陀螺仪相似，与式(1)～(3)类似来计算。

位置精度测试采用径向误差率(Radial Error Rate,RER)及其圆概率误差(Circular Error Probability,CEP)的指标来衡量，速度和航姿信息精度测试采用均方根(Root Mean Square,RMS)误差来衡量[5]。

4）径向误差率及圆概率误差

假设某次SINS性能测试评估实验中共进行了M次采样，第i次采样时SINS输出的纬度值为Li，经度值为λi，计算得到的基准纬度值为L0i，基准经度值为λ0i。则第i次采样时的纬度误差为ΔLi=Li-L0i，经度误差为Δλi=λi-λ0i。则计算第i次采样时的位置径向误差率为：

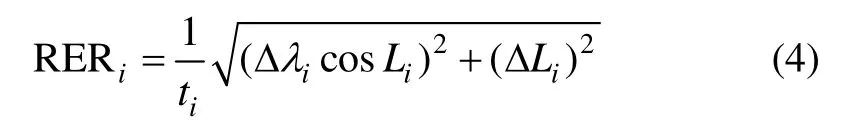
式中，ti为SINS进入导航状态时刻到第i次采样时所经过的时间，单位为h。

在实验次数较多的情况下，圆概率误差可以用公式统计为：

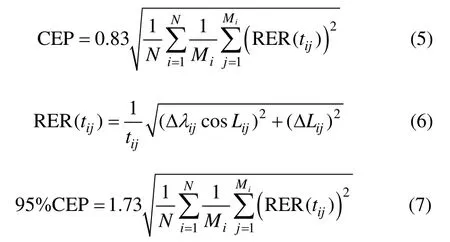
式中，N为有效实验次数，Mi为第i次实验采样点数，为第i次实验第j个采样时刻的径向误差率。tij、Δijλ、ΔLij、Lij分别为第i次实验第j个采样时刻的导航时间、经度误差、纬度误差和纬度真值。

5）速度均方根误差

速度精度采用速度误差的均方差来衡量，也称为均方根值，记为RMSv，计算公式为：

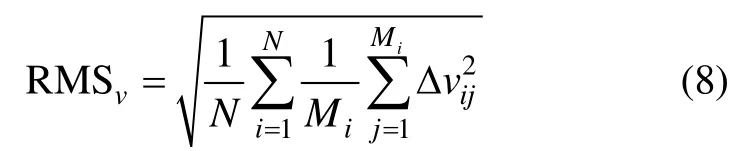
式中，RMSv为速度的平均均方根值，Δvij为第i次实验第j个采样时刻的速度误差，单位为m/s。

6）航姿信息均方根误差

航姿信息精度采用其误差的均方差来衡量，也称为均方根值，记为RMSθ，计算公式为：

式中，RMSθ为俯仰角(或滚转角或偏航角)的平均均方根值，Δijθ为第i次实验第j个采样时刻的航姿信息的误差，单位为角分。

1.2 稳定性测试

SINS稳定性测试主要包括单个飞行模态测试和多个飞行模态测试。单个飞行模态测试包括单一平飞模态、爬升/下滑模态和左转/右转飞行模态等测试，多个飞行模态指飞行模态切换阶段的测试和多个飞行模态的测试。通过多位专家对各测试进行定性描述来评估SINS的性能优劣。

1.3 可靠性测试

可靠性测试主要包括对 SINS故障检测能力和容错能力[8]。SINS故障检测测试主要包括可靠度和SINS平均无故障工作时间；SINS故障诊断测试主要指SINS故障的可修复能力，包括修复率和平均修复时间。

1）可靠度

可靠度是对系统或产品在规定的条件下和规定的时间内，完成规定功能能力的概率度量，通常用R来表示：

式中，t为规定的时间，T表示系统或产品的寿命。

2）平均无故障工作时间

平均无故障工作时间（Mean Time Between Failure,MTBF）指系统或产品相邻两次故障间的平均工作时间。

式中，n为测试的产品总数，ni为第i个测试产品的故障数，tij为第i个产品的第j-1次故障到第j次故障的工作时间，N为测试产品的所有故障数。

3）修复率

修复率指修理时间已达到某一时刻但尚未修复的产品在该时刻后的单位时间内完成修理的概率，可以用μ(t)来表示：

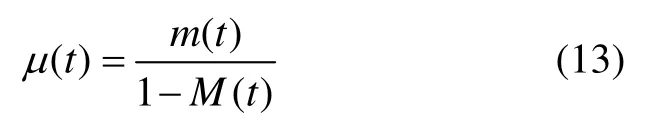
式中，m(t)为维修时间t的概率密度函数，M(t)为规定的条件下使用的产品发生故障后在规定的时间(0,t)内完成修复的概率。

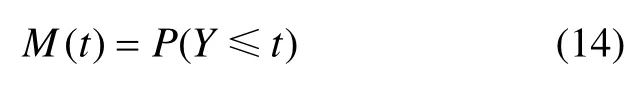
式中，Y为故障诊断、维修准备及维修实施时间之和。

4）平均修复时间

平均修复时间(Mean Time To Repair,MTTR)是指可修复产品的平均修理时间，其估计值为修复时间总和和修复次数之比。

式中，t为维修时间，M(t)为规定的条件下使用的产品发生故障后在规定的时间(0,t)内完成修复的概率。

2 SINS性能测试综合评估算法

2.1 三级多源信息融合结构

基于三级多源信息融合结构的SINS性能测试综合评估算法框架如图2所示。一级融合是多个专家对SINS性能测试子指标采取模糊评判的方法获得融合时所需的基本置信指派，消除性能测试测试子指标模糊评价带来的影响；二级融合将一级融合得到的多个专家对同一测试指标下的各测试子指标的评估意见进行融合，得到对测试指标的融合结果；三级融合是将各测试指标的融合结果进行再融合，得到对SINS性能测试评估的结果。

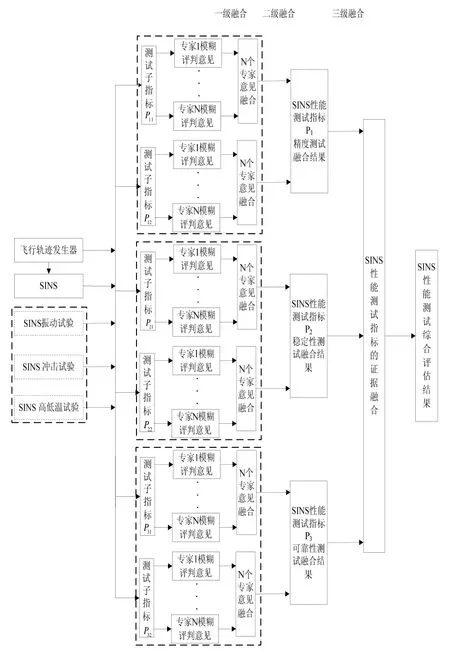
图2 SINS性能测试综合评估算法框架Fig.2 Framework of SINS performance testing and evaluation algorithm

基本思想是利用飞行轨迹发生器为测试评估提供基准轨迹数据，由测试基准轨迹数据求解出SINS的激励信号比力和角速率，以此激励SINS解算得到SINS输出轨迹数据，并通过多个领域专家根据SINS性能变化规律的知识对构建的性能测试底层子指标进行分析，给出对应的性能测试子指标模糊评判，由于对底层子指标的评价中包含一定的不可靠和不完全信息，需要运用模糊理论的知识，对专家的模糊评判意见进行量化描述，再者不同专家由于具有不同的工作经验和知识水平等因素，由多个性能子指标对SINS进行性能测试评估，也存在着一定的不确定性和冲突性。采用LCD-DST组合规则对专家给出的评估意见进行逐级融合，准确、实时给出科学的评估结论。由于框架采用模块化设计结构，便于模块的修改和扩展，还可将SINS振动试验、冲击试验、高低温试验等作为SINS性能测试评估的一部分。

2.2 不确定信息的专家评估

考虑N个专家或者智能体 {x1,x2,…,xN}构成的专家群体对某SINS性能测试的优劣进行综合评定，SINS性能评价结果等级分为{A1：优,A2：良,A3：中,A4：差}。通常专家对比较抽象的难以量化的定性指标，对此评判多依赖于自身的知识水平、工作经验等因素，因此常采用“大致”、“可能”等模糊词语表述更符合客观实际和人的表达方式。

假设模糊评语集定义为U={肯定、很可能、大致可能、可能、大致不可能、不可能、绝对不可能}，再构造与评语集对应的数量7元组V=｛v1,v2,…,v7｝可以充分灵活的定量表达专家的模糊评语，其中vi为第i个评语元素在[0,1]之间的实数表示，则设定的各模糊评语采用数量7元组表达如表1所示。

表1 模糊评语的表示Tab.1 The representation of fuzzy comment

再构造与评语集对应的性能测试评价集，来充分定量表达各模糊评语，将划分的 SINS性能等级进行量化表达。性能测试评价集的表示如表2所示。

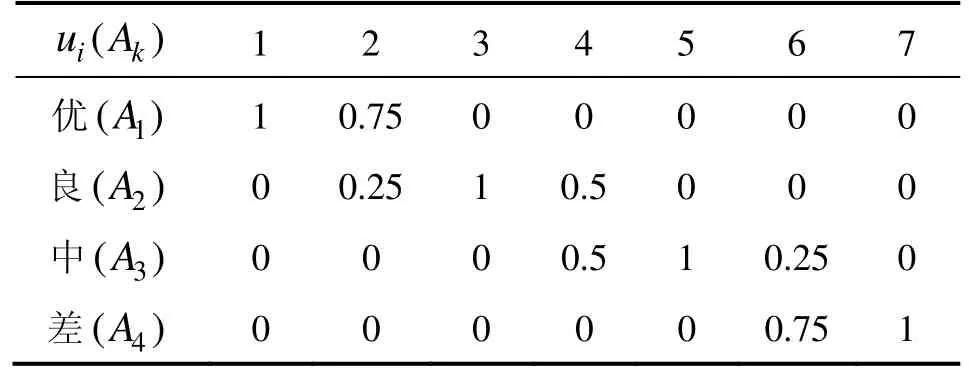
表2 性能测试评价集的表示Tab.2 Representation of performance test evaluation set

根据模糊数学知识，可以得到专家j对性能测试子指标Prt的模糊评语到性能等级中每个等级元素的隶属度函数为：

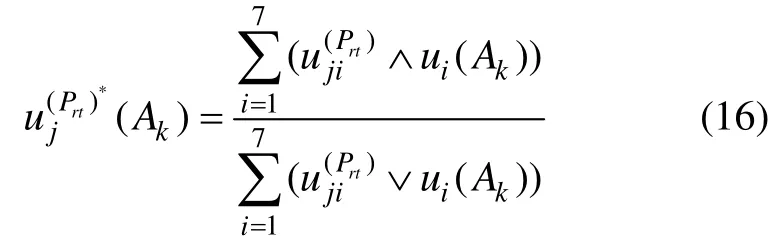
式中，k= 1,2,3,4；j= 1,2,…,N；r= 1,2,…,M；t= 1,2,…,Z；∧表示min运算；∨ 表示max运算。式(16)中，它表示专家对性能测试子指标的模糊评语与等级中每个等级的匹配程度，由于表1中的各模糊评语的定义难以完全独立，可能所有匹配值的和不为1，需要进行归一化处理：

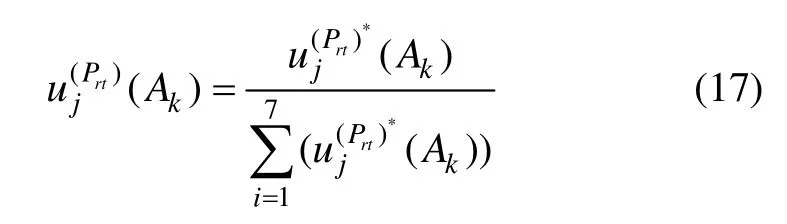
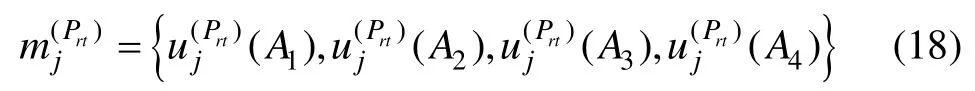
2.3 基本置信指派的构造

证据理论通过定义在辨识框架上的焦元及其基本置信指派来表示信息，因此基本置信指派的获取是采用证据理论进行多源信息融合的前提条件。基本置信指派的构造一直是DST证据理论中的关键问题和难题，由于其应用背景的复杂性和多样性，因此，无法给出一般形式，根据研究内容和对象的不同，所采用的方法也有所不同。

由于各个专家在理论知识、工作经验以及学历层次上有所不同，因此，对任一性能测试子指标Prt(1≤r≤M;1≤t≤Z)的评判意见不一定可靠，需要根据学术能力、工作经验水平与学历层次上的评价通过打分进行重要性评定，可得专家j(j=1,2,…,N)评判意见的权重因子：

专家群体中权重越高的专家其评判意见的可靠性越高，不仅要考虑自身的经验和主观偏好系数，而且还要考虑与权重最高的专家评判意见的差异。则专家j(j=1,2,…,N)对性能测试子指标Prt评判的可靠度系数[9]为：

式中，Prt表示第r测试指标下的第t个测试子指标，往往在一区间[0.9,1]内，其值可根据蒙特卡洛法从[0.9,1]中模拟得到。

DST基本概念：设Θ为一非空有限集合，R为辨识框架幂集2Θ中的一个类，在R上定义基本置信指派函数(mass函数)，m:R→ [0,1]，满足：

由DST证据理论可知，上述具有不确定信息的专家意见表示形式需要满足mass函数的性质，将性能参照等级集作为识别空间，按照mass函数的定义，专家j(j=1,2,…,N)对系统性能测试子指标Prt评判意见的基本置信指派为：

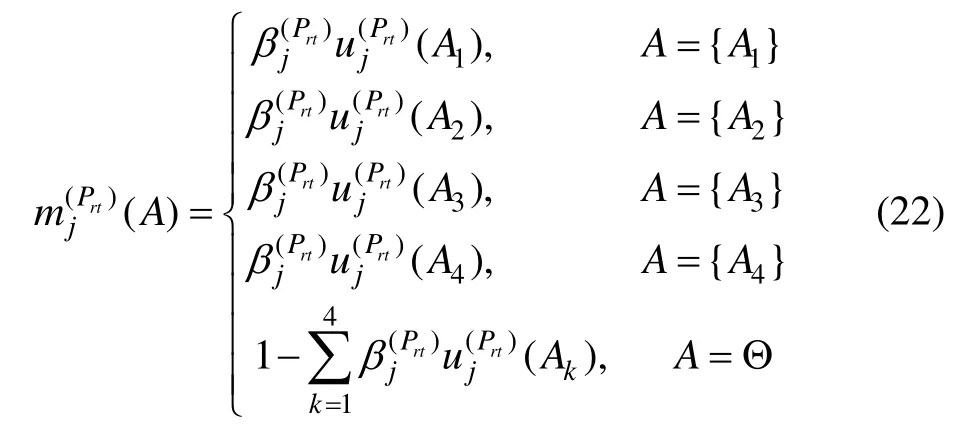
对多个专家的不确定性评判意见进行融合时，往往会遇到专家之间意见不一致或相悖的情况，需要选择改进的DST组合规则进行融合，获得更为可靠的性能测试评价结果。

2.4 局部冲突分配的DST组合规则

假设辨识框架Θ下条件独立的两个证据，其焦元分别为bi和cj(i=1,2,…,n;j= 1,2,…,m)，其基本置信指派函数分别为m1和m2，则DST组合规则可表示为：

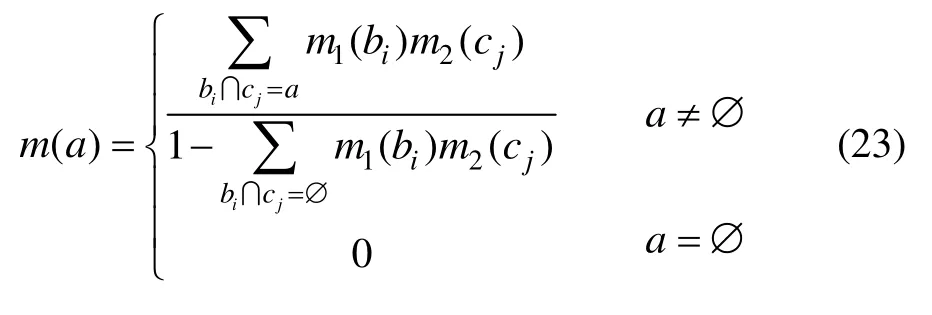
DST组合规则由于归一化计算导致冲突信息的不合理分配，通过利用焦元距离获取证据源的权重因子，并分析局部冲突产生的原因，将冲突焦元提供的信息进行局部分配[7]。假设有n个相互独立的证据，m个不同的焦元，对于证据中的某一个焦元来说：

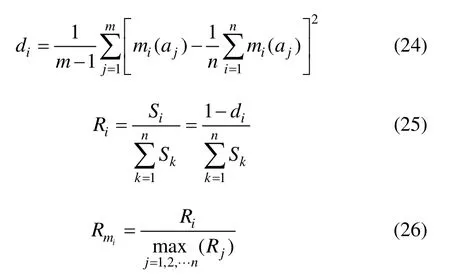
式中，di为证据mi的焦元距离，Si为证据mi的相似度，Ri为证据mi的相对可信度，Rmi为证据mi的信任度。

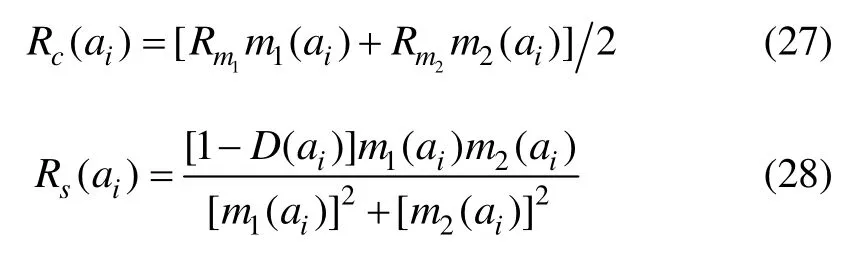
式中，Rc(ai)为焦元ai的信任度，Rs(ai)为焦元ai的相似度，如果Rs(ai)不为零，则需要进行归一化处理为相对相似度Rrs(ai)，表示如下：

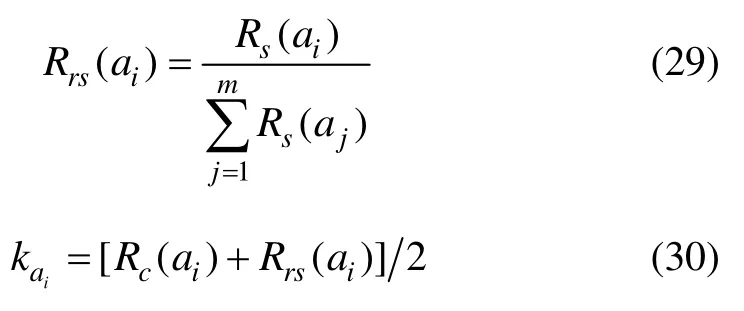
式中，kai为焦元ai的冲突权重因子。

则LCD-DST组合规则可表示为：

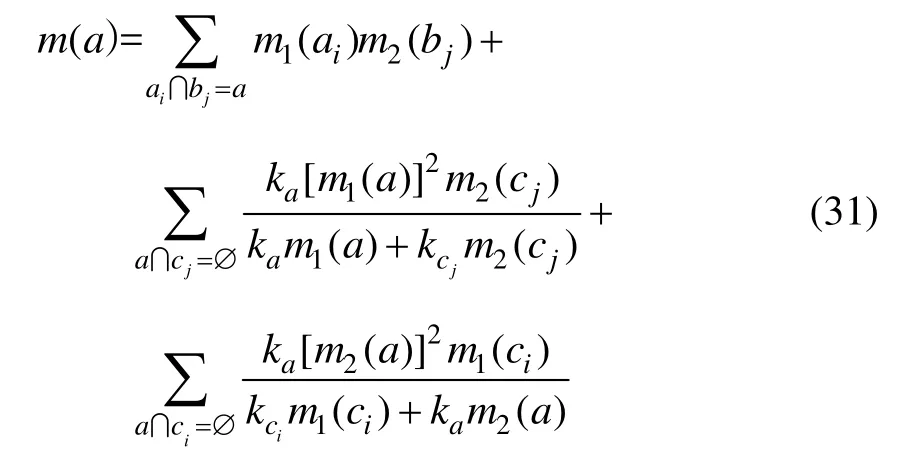
2.5 算法计算步骤

基于三级多源信息融合结构的SINS性能测试综合评估算法的计算步骤如下：

Step1：首先根据SINS性能测试底层子指标通过比较计算获得性能测试子指标所需的实验数据。

Step2：选择N个专家组成的评估专家群体，通过专家对构建的SINS测试评价体系中的性能测试子指标进行评价，得到模糊评判意见。

Step3：根据N个专家的评判意见和评判指标的模糊评语以及性能等级中每个元素的隶属度函数，计算得到专家的评判意见属于SINS性能参照等级的优、良、中、差的程度。

Step4： 采用层次分析法(Analytic Hierarchy Process,AHP)[10]或打分法求取各个专家的权重因子，假设随机取得主观偏好系数计算得到各个专家的相对可靠度。

Step5：建立N个专家关于每个性能测试子指标的可信度mass函数，然后再对得到的各个子指标的综合性能等级进行向上综合，进而得到顶层性能测试评估的综合性能等级的表达。

Step6：利用LCD-DST组合规则对专家的性能子指标评价进行逐级融合获得更为可靠的性能优劣评估结果。

3 仿真结果分析

为了验证本文提出的基于三级多源信息融合结构的SINS性能测试综合评估算法的性能，利用专家系统对评价子指标进行性能优劣等级测评，将基于LCD-DST组合规则结合SINS测试评估体系，对SINS性能测试进行综合评估。

选择N=5位专家组成的评估群体，从构建的性能测试子指标进行评判SINS的性能优劣，5位专家根据自己的专业知识和工作经验等，综合分析实验数据和系统性能测试底层子指标，对性能测试子指标采用模糊词语集U={肯定、很可能、大致可能、可能、大致不可能、不可能、绝对不可能}来表示SINS的性能等级优劣。其对各性能测试子指标的相关评判意见如表3所示。

表3 专家对各性能测试子指标的相关评判意见Tab.3 Performance testing subindex opinion of experts

根据式(16)计算专家j(1≤j≤5)对 SINS性能测试子指标Prt的模糊评语为“很可能”到性能等级中等级元素为1A的隶属度函数为：

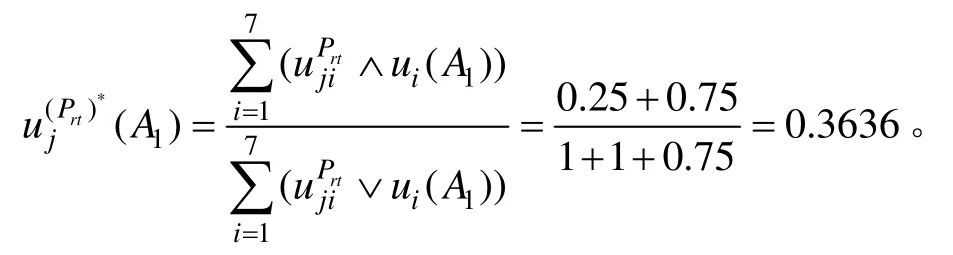
由于模糊评语为“很可能”到性能等级中等级的所有隶属度函数之和不为1，需要进行归一化，可得：

同理可得到专家对SINS性能测试子指标为“肯定”、“很可能”、“大致可能”、“可能”、“大致不可能”、“不可能”、“绝对不可能”的评判意见相对性能等级是优、良、中、差程度的归一化表示如表4所示。

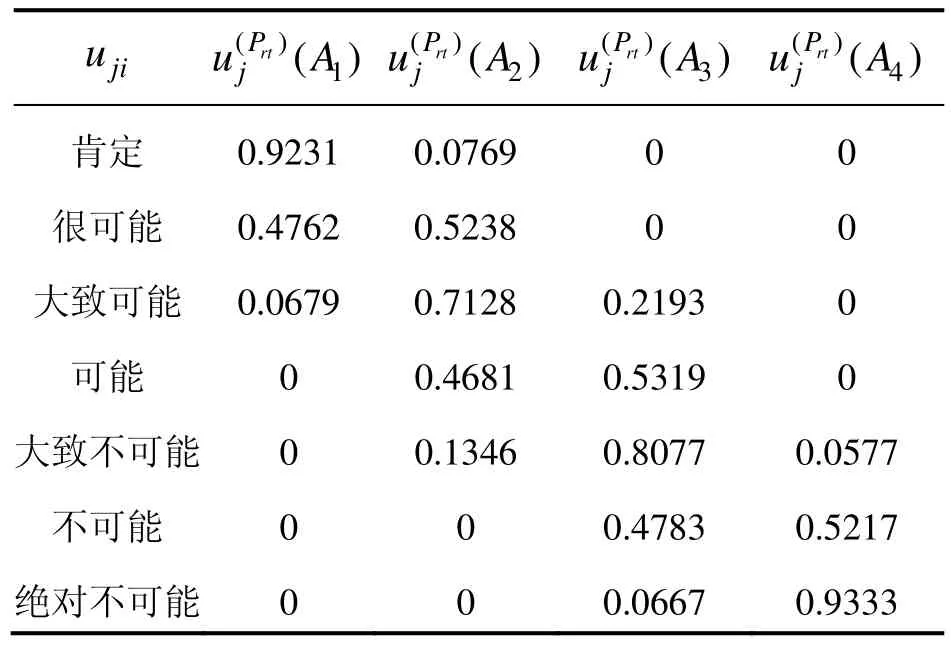
表4 各性能测试子指标测试评价集的归一化表示Tab.4 Normalization representation of performance testing subindex test evaluation sets

采用打分法求取 5位专家的权重因子{0.25,0.16,0.19,0.18,0.22}，假设随机取得系数为0.92，则由式(20)可求得各专家的相对可靠度为：。然后建立5位专家关于每个性能测试子指标的评估优劣的mass函数，构成五个相互独立的证据，分别记为m1,m2,m3,m4,m5。通过 5位专家对P11给出的测试评价集构成各专家对性能测试子指标P11评估的证据源，计算得5个证据的相对可信度分别为 0.1969、0.2038、0.2041、0.2022、0.1930。综合分析各专家对性能测试子指标P11测试给出的五个证据信息可以看出，专家5可能由于自身知识或经验不足等因素，导致与其他专家的评价意见相冲突。利用DST组合规则和LCD-DST组合规则进行融合分别得到专家对性能测试子指标P11的融合结果如表5所示。

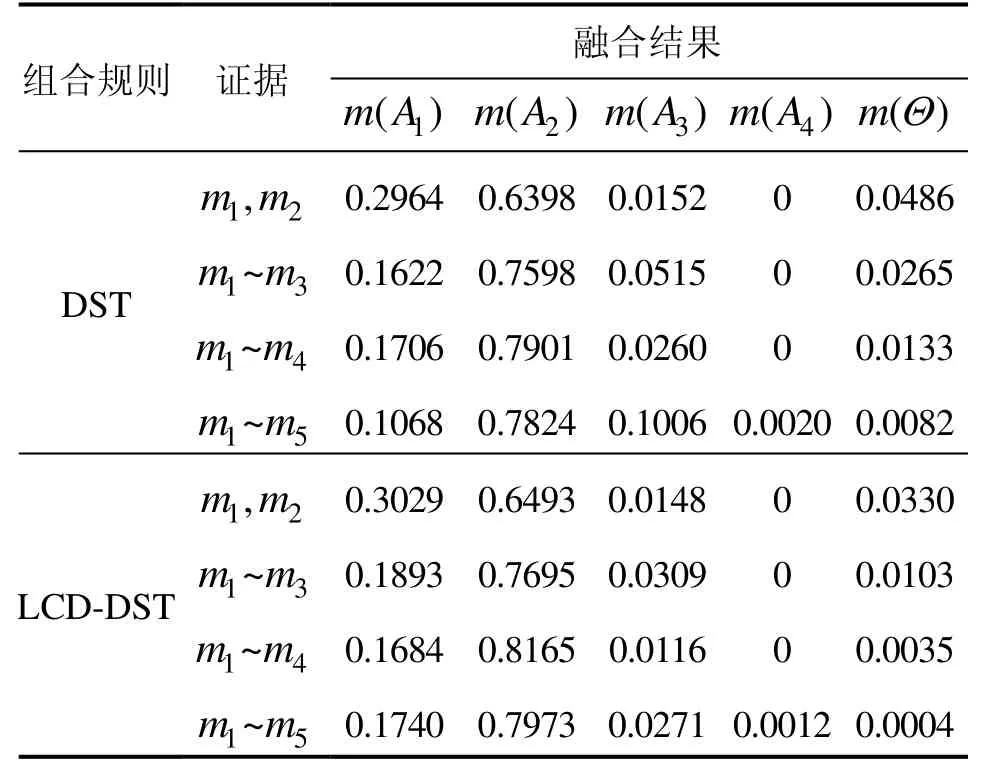
表5 专家对性能测试子指标P11的融合结果Tab.5 Combination results of performance test subindexP11

同理，通过上述方法分别采用DST组合规则和LCD-DST组合规则对SINS性能测试的各性能子指标的多个专家评价意见分别进行融合，获得专家对各性能子指标的融合结果如表6所示。

表6 专家对性能测试子指标的融合结果Tab.6 Combination results of performance test subindex

利用AHP法求得P11、P12性能测试子指标的相对权重为(0.4,0.6)，假定模拟取得的系数均为0.93，再对P11、P12的指标函数进行融合，可以得到上一级指标的mass函数。同理分别求取其余两个性能测试指标P2、P3的mass函数，再求出指标的相对重要度如(0.33,0.36,0.31)以及系数0.93，并进一步对三个性能测试指标的mass函数进行融合，得到整个SINS性能测试评估的优劣等级。通过根据表6中的各个指标的融合结果进行上一级的融合获得对SINS性能测试评估的结果。

利用DST组合规则和LCD-DST组合规则进行信息融合分别得到专家对各性能测试指标的融合结果如表7所示。

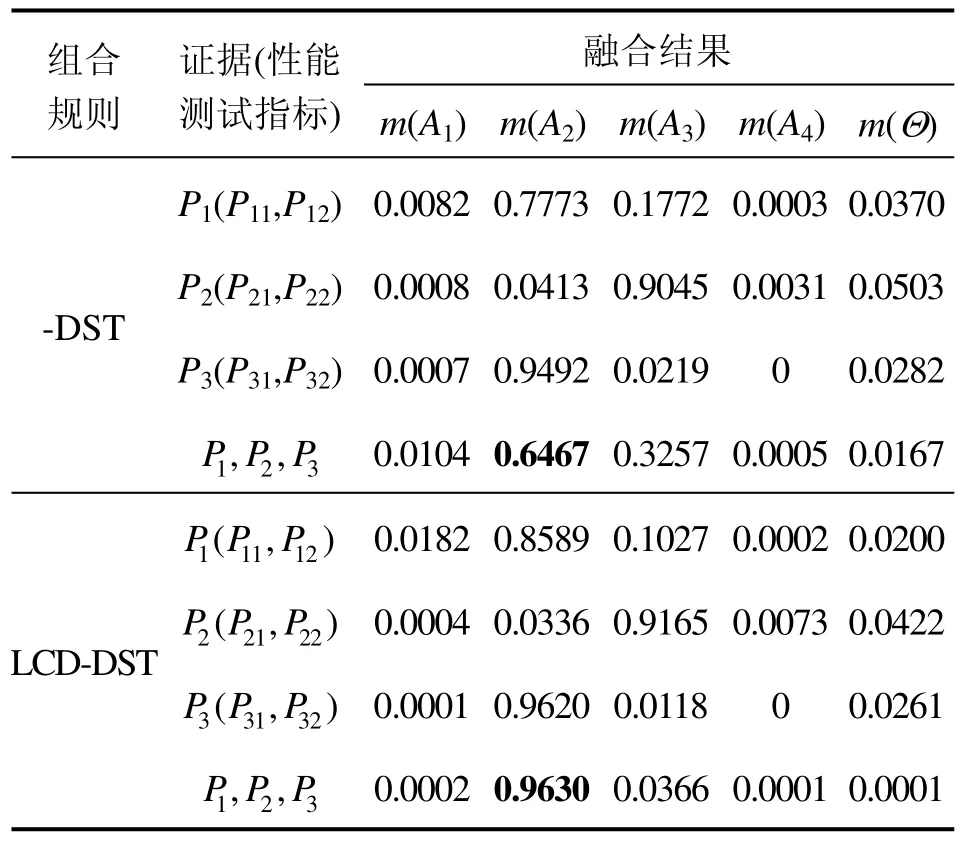
表7 专家对各性能测试指标的融合结果Tab.7 Combination results of performance test index

综合表7中的单一SINS性能指标的融合结果数据可知，性能测试指标P2的mass函数与性能测试指标1P、3P的mass函数存在冲突现象，其SINS性能评估融合结果应该是属于等级良的可能性最大，相对于采用DST组合规则得到良的基本置信指派值为0.6467，采用LCD-DST组合规则得到良的基本置信指派值为0.9630，则LCD-DST组合规则融合效果明显优于DST组合规则。

4 结 论

针对 SINS性能测试综合评估中存在指标多、不确定性等问题，本文建立了 SINS性能测试的评估指标体系，并将LCD-DST组合规则引入SINS性能测试评估中，提出了一种基于三级多源信息融合结构的SINS性能测试综合评估算法。根据多个专家对性能测试子指标的模糊评语和性能测试评价集，得到各专家对每个性能测试子指标的意见属于性能参照等级的优、良、中、差程度，由专家的学术能力、工作经验水平等不同来确定各专家的评判意见的权重因子和对性能测试子指标评判的可靠度系数，由此构造对性能测试子指标评判的置信指派。然后，对多个专家给出的各性能测试子指标通过LCD-DST组合规则进行逐级融合，最后，得到 SINS性能测试评估结果。通过仿真实验验证了该算法能够更好的获取 SINS性能测试评估的结果。

（References）：

[1]Ali J,Mirza M R U B.Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution[J].Nonlinear Dynamics,2010,61(3): 491-502.

[2]Sun W,Xu A G,Che L N,et al.Accuracy improvement of SINS based on IMU rotational motion[J].IEEE Aerospace and Electronic Systems Magazine,2012,27(8): 4-10.

[3]李军伟，程咏梅，陈克喆，等.基于飞行仿真的捷联惯导算法测试平台[J].中国惯性技术学报，2012，20(5)：530-535.LI Jun-wei,CHENG Yong-mei,CHEN Ke-zhe,et al.Test platform for SINS algorithm based on flight simulation [J].Journal of Chinese Inertial Technology,2012,20(5): 530-535.

[4]Gyro and Accelerometer Panel of IEEE.IEEE standard specification format guide and test procedure for single axis laser gyros[S].New York: IEEE Aerospace and Electronic Systems Society,2006: 1-83.

[5]万世春.惯性导航系统的精度测试方法[J].导航，2006，42(3)：83-87.WAN Shi-chun.Accuracy measurement method for INS[J].Navigation,2006,42(3): 83-87.

[6]Li X D,Dezert J,Smarandache F,et al.Evidence supporting measure of similarity for reducing the complexity in information fusion[J].Information Sciences,2011,181(10): 1818-1835.

[7]李军伟，程咏梅，潘泉，等.基于焦元距离的冲突证据组合规则[J].系统工程与电子技术，2010，32(11)：2360-2362.LI Jun-wei,CHENG Yong-mei,PAN Quan,et al.Combination rule of conflicting evidence based on focal element distance[J].Systems Engineering and Electronics,2010,32(11): 2360-2362.

[8]Peiravi A.Redundancy for reliability growth of electronic systems under various operating conditions[J].Journal of Applied Sciences,2009,9(16): 2941-2947.

[9]黄炎焱，杨峰，王维平，等.仿真数据综合可信度的测度与校验方法研究[J].系统工程学报，2008，23(4)：479-487.HUANG Yan-yan,YANG Feng,WANG Wei-ping,et al.Research on method of measurement and verification on comprehensive credibility of simulation data[J].Journal of Systems Engineering,2008,23(4): 479-487.

[10]蔡体菁，陈鑫巍.基于层次分析法的重力匹配区域选择准则[J].中国惯性技术学报，2013，21(1)：93-96.CAI Ti-jing,CHEN Xin-wei.Selection criterion based on analytic hierarchy process for matching region in gravity aided INS[J].Journal of Chinese Inertial Technology,2013,21(1): 93-96.

Comprehensive evaluation algorithm of SINS performance testing based on three-level multi-source information fusion structure

LI Jun-wei1,2,CHENG Yong-mei1,CHEN Ke-zhe1
(1.School of Automation,Northwestern Polytechnical University,Xi’an 710072,China; 2.School of Computer and Information Engineering,HeNan University,Kaifeng 475004,China)

In view of the problems in SINS performance test,such as uncertainty and too many indices etc.,a comprehensive evaluation algorithm of the SINS performance test is proposed based on three-level multi-source information fusion structure.The proposed index system of the SINS performance test includes accuracy,stability and reliability performance testing index and 16 performance testing bottom subindices.Many experts are invited to evaluate the credibility of the bottom subindex data in order to obtain the fuzzy assessment corresponding to subindex and construct the mass function of each expert’s evidence.The structural framework of the SINS performance testing and evaluation is built.The improved combination rule based on local conflict distribution can be used to obtain the results of SINS performance comprehensive testing and evaluation by three-level evidence fusion.The simulation results show that,compared with the traditional Dempster-Shafer theory(DST) method,the proposed algorithm can not only evaluate the SINS performance,but also enhance the reliability of the evidence combination results.

SINS; performance evaluation; expert system; fuzzy evaluation; information fusion

U666.1

：A

1005-6734(2014)02-0177-08

10.13695/j.cnki.12-1222/o3.2014.02.007

2013-11-25；

：2014-03-04

航空科学基金项目（20100853010）

李军伟（1981—），男，博士研究生，从事惯性导航与制导、飞行仿真等研究。E-mail：lijunwei@mail.nwpu.edu.cn

联 系 人：程咏梅（1960—），女，教授、博士生导师。E-mail：chengym@nwpu.edu.cn