蒙古国及其周边地区地震分形维度及b值研究①

徐伟进，高孟潭

（中国地震局地球物理研究所，北京 100081）

0 引言

地震活动性参数是指采用地震的时空强等信息，根据统计模型回归得到的参数值，其与地质构造、岩石力学性质、地下介质物性以及震源机制等有密切的关系。其中相关性维度D值、震级—频度关系式中b值、大森定律中的p值是地震学研究中三个重要的参数。研究这些参数的时空变化对于了解研究区的构造环境、应力环境、介质物性变化以及震源特性等有重要的科学意义。

地震活动性的分形特性指的是地震在时间和空间分布的随机自相似结构，其可以使用分形维度D值来表示，根据D值的大小可确定地震在空间是随机分布还是聚集分布的［1－2］。分形维度也可能用来定量描述某一断层系统地震活动的差异程度，这时D值主要受应力场分布、地质、力学及构造差异等因素的控制。分形维度值为判断一个地区是否处于稳定状态提供了十分重要的信息。分形维度值的任何变化都意味着地区系统状态的改变。

地震学中另一个基本参数为震级—频度关系式中的b值，从数学上讲，b值表示的是某一地区全体地震中不同震级档地震的比例关系。从物理上讲，b值与众多地质构造特征相关。Mogi［3］研究表明b值与地下介质的各向异性程度及演示裂缝密度有关。然而Scholz［4］的研究却认为应力状态与b值的大小密切相关。此外还有研究表明随着深度的增加b值有逐渐减小的趋势［5］。这可能是由于随着深度的增加应力也在增大的原因。由此可见深入研究地震活动参数对于了解研究区的地震危险性具有重要的作用。

目前关于蒙古国地区的b值及分形维度D值的研究还比较少见，本文采用蒙古国及其周边地区的地震目录，较为系统的研究了蒙古国地区地震b值和D值的空间分布特征及随深度变化的规律。并初步分析了二者之间的关系。

1 数据及研究区

文中采用的地震目录数据是中蒙两国地震工作者共同收集整理的地震目录数据。根据徐伟进等［6］对蒙古国及周边地区地震目录的分析结果，我们选取了完整可靠的地震目录来计算地震活动性参数。选取地震目录的起始记录时间为1977年，最小完整起始震级为Mc＝3.5。

为了揭示地震活动性参数的空间差异性，我们根据蒙古国及其周边的地质构造，并结合地震活动性分布情况划分了10个研究区域（图1）。用编号表示研究区域的名称，如An表示第n个研究区域。其中A0表示整个研究区域。分别计算了每个研究区域内的b值和D值。

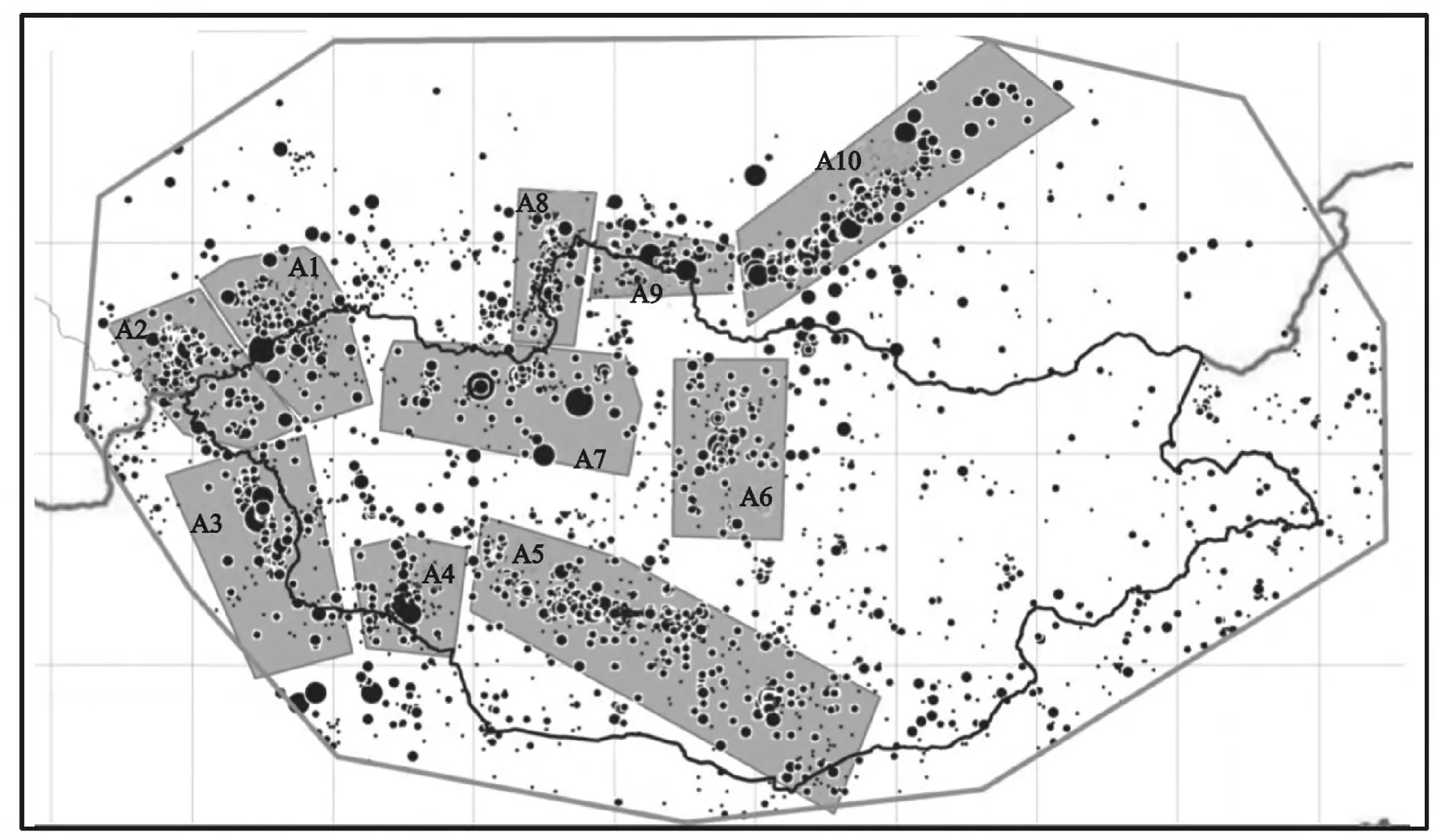
图1 蒙古国地震空间分布及研究区示意图Fig.1 Spatial distribution of earthquakes（M≥3.5）reported in the Mongolia’s seismic catalog and the study areas（gray areas）

2 地震活动性参数估计

2.1 分形维度计算

分形维度是通过相关维度来进行估计的。相关维度是一种用来定量描述空间自相似特征的工具［7］。相关维度的数学定义为：

其中C（r）为相关函数，可写为

其中H为阶跃函数，当x≤0时H（x）＝0，当x＞0时H（x）＝1。为两点之间的欧拉距离。本文中只考虑了二维空间两点之间的距离。给定大量的数据点和一个小的相关距离r，则相关函数C（r）和相关距离r呈现幂律关系：

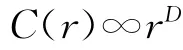
其中D即为文中所描述的分形维度。通过计算lgC（r）与lgr关系式的斜率即可得到分形维度值D。本文中我们计算的是二维空间地震空间分布的相关维度值D，相关维度值的取值区间为1.0～2.0。

2.2 b值估计

一般来说，小震的发生频度要比大震高的多，大小地震的比例关系可用Gutenberg and Richter［8］提出的关系式来表征：

上式即为 Gutenberg－Richter Frequency－Magnitude（简称G－R关系），其中N（m）为震级大于等于m的地震频数，a、b为参数，可用实际地震目录回归得到。关于b值估计，常用的主要有最大似然和最小二乘法两种方法。Hirata［2］认为最大似然法优于最小二乘法，在样本较小的情况下最大似然法得到的结果更稳定。故本文中我们采用最大似然法进行b值估计。Utsu［9］给出的最大似然法计算b值的公式为：

3 结果分析

采用上述的计算方法我们分别估计了10个研究区及整个蒙古国地区删除余震之前和删除余震之后地震目录的b值及相关维度D值（表1）。整个蒙古国地区删除余震后地震的空间相关维度约为1.56，这表明蒙古国地区地震空间分布不是完全随机的，具有一定的丛集度，只是丛集度相对较低。未删除余震的地震目录空间相关维度值为1.11，比起删除余震后空间相关维度有较大幅度减小，说明地震的空间丛集度增大，这是由于余震丛集造成的。观察10个研究区的相关维度值（表1第2、3列）我们发现各个研究区的相关维度值具有一定的差异。相对较大的D 值出现在A1、A2、A3、A4、A5、A7研究区内，这些区域位于蒙古国的西部和南部地区，正是蒙古国活动断裂发育的地区。D值较大说明这些区域地质结构的各向异性更为突出［10］。

一般认为，在一个活动构造区b值趋于1.0，变化范围在0.5～1.5之间［5，11］。Ulziibat等［12］采用蒙古国1902—2002年M≥3.0以上地震计算得到的蒙古国地区b值为0.8。我们的研究中蒙古国地区的b值约为0.962（删除余震后），非常趋于1.0。造成这一差别的主要原因在于Ulziibat采用的地震目录小震有缺失。根据徐伟进等［6］的研究表明蒙古国及其周围地区1977年以后M≥3.5的地震目录才基本完整。因此Ulziibat采用的1902年以后的M≥3.0地震目录是不完整的，目录中小震大量缺失从而导致b值变小。本文中采用未删除余震的地震目录计算得到的b值约为0.943，和删除余震后计算得到的b值基本相同，这说明蒙古国地区目前处于应力稳定的状态，或者说蒙古国地区目前主要受同一区域应力场的控制。通过比较各研究区的b值（表1第4、5列），我们发现各个研究的区的b值也具有一定的差异，这说明了各个研究区应力状态的不同。最大的b值出现在A1区，采用删除余震后的目录计算得到的b值为1.148，未删除余震计算得到的b值为1.248，b值较大说明了A1区各向异性较为突出，且目前处于较低的应力积累状态，小震活动频繁，地震活动强度较弱。最小的b值出现在A2区，为0.816（删除余震后），未删除余震的b值为0.622，这说明了A2研究区强余震活动较为活跃，A2区应变积累水平较高，地震活动强度大。A2研究区的b值与整个蒙古国及周边地区的b值差异较大，也说明了A2研究区目前主要受局部应力场的控制，并且应力场分布差异较大。此外b值较低的研究区还有A10区，A10区为贝加尔湖断裂地区，该区应力水平相对较高，应力场分布也较为复杂。

表1 各研究区D值及b值分布Table 1 The fractal correlation dimension（D）and seismic b－value at different study areas

进一步地，我们计算了蒙古国地区0～10km、10～20km、20～30km三个深度的相关维度D值和b值（表2）。通过表2第3列可以看出在10～20km深度相关维度D最大，这说明蒙古国及周边地区在这一深度地壳介质结构各向异性最为突出。20～30 km深度处的D值较20km以上有较大幅度的减小，说明这一深度的地壳介质结构相对较为均匀，地震分布更集中。本文计算的b值在0～10km深度处的值最大，10km以下b值相对较小。Mori等［13］和 Wiemerand Wyss［5］研究认为随着深度增加，压力也增加从而导致b值减小。Gerstenberger等［7］的研究表明，b值随深度增大而减小的物理原因主要有应力变化和介质的各向异性。本文计算结果表明在蒙古国地区地壳的最上层b值最大，这意味着地壳最上层结构各向异性最突出，也可能暗示组成地壳最上层的岩石强度较低［15－16］。Wyss等［17］的研究表明在某些地区b值与深度没有系统的对应关系，即b值不随深度的增加持续的增大或减小。本文中b值在10km以下也不是随深度增加而减小的，而是在10～20km深度处b值最小，这说明蒙古国地区地壳在这一深度处应力水平最高，应力分布不均匀［10］。

本文还初步研究了蒙古国地区地震b值和D的相关性。关于G－R关系中的b值和分形维度D值的关系近几十年来得到了广泛的研究（Aki 1981；Hirata 1989；Oncel et al.1996；Legrand 2002；Wyss et al.2004）。Aki（1981）首先提出了一种简单的b值和D 值的统计关系式D＝3b／c（c＝1.5）。目前的研究中b值和D值的关系主要有正相关［19，21］和负相关性［2，18］。本文根据上文计算得到的22个b值和D值样本初步分析了二者之间的关系。从图2中的数据点可以看出随着b值的增大，D值也有变大的趋势，支持二者呈正相关的结论。只是本文中得到的二者关系式并不支持Aki（1981）的关系式。这是由于Aki（1981）计算的是三维分形维度值，而本文中计算的是二维分形维度值，两个维度值的取值范围不同，因此两个关系式的斜率自然不同。另外本文中样本点只有22个，样本量较小，回归的关系式误差较大，不能代表一般情况，但是支持正相关的结论。

表2 不同深度处的D值和b值Table 2 The Fractal correlation dimension（D）and seismic b－value at different depths

图2 b值和D值的相关性（蓝线为Aki（1981）的关系曲线，红线为本文结果）Fig.2 Relationship between the b－value of the Gutenberg－Richter relation and the fractal dimension D（blue line indicates Aki’s relation，red line indicates our result）

4 结论

本文根据蒙古国及其周边地区的地震目录，计算了G－R关系中的b值和分形维度值D。结果表明蒙古国地区的b值为0.962（删除余震后），非常接近于1，说明蒙古国地区是一个典型的构造活动区［5，11－12］。计算得到的蒙古国地区地震的分形维度值D为1.56（删除余震后），该值小于2，说明蒙古国地区地震空间分布具有一定的丛集性，只是丛集程度不高。通过比较10个研究区的b值和D值，发现二者在空间上都具有差异性，说明蒙古国地区应力分布和地壳介质结构具有空间差异性。

文中计算了0～10km、10～20km和20～30 km三个深度处的b值和D值。结果表明20～30 km深度处的D值较20km以上有较大幅度的减小，说明这一深度的地壳介质结构相对较为均匀，地震分布更集中。计算得到的蒙古国地区地壳最上层b值最大，这意味着地壳最上层结构各向异性最突出，也可能暗示组成地壳最上层的岩石强度较低［15－16］。b值在10km以下不符合Wiemerand Wyss［5］的研究结果随深度增加而减小，而是在10～20km深度处b值最小，这说明蒙古国地区地壳在这一深度处应力水平最高，应力分布不均匀［10］。

此外文中还初步分析了b值和D值二者的关系，结果表明二者呈现正相关性。

（References）

［1］OgatamY.Statistical Models for Earthquake Occurrences［J］.J Am Stat Assoc，1988，83：9－27.

［2］Hirata T.A Correlation Between the B－value and the Fractal Dimension of Earthquakes［J］.J Geophys Res，1989，94：7507－7514.

［3］Mogi K.Earthquakes and Fractures［J］.Tectonophysics，5：35－55.

［4］Scholz C H.The Frequency－Magnitude Relation of Micro Fracturing in Rock and its Relation to Earthquakes［J］.Bull Seismol Soc Am，1968，58：399－415.

［5］Wiemer S，M Wyss.Mapping the Frequency－magnitude Distribution in Asperities：An Improved Technique to Calculate Recurrence Times［J］.J Geophys Res，1997，102：15，115－15，128.

［6］徐伟进，高孟潭，李宗超.蒙古国及其周边地区地震目录初步分析［J］.震灾防御技术，2014，（待刊）.XU Wei－jin，GAO Meng－tan，LI Zong－chao.A Preliminary A－nalysis of the Seismic Catalogs Reported in Mongolia and Surrounding Area［J］.Technology for Earthquake Disaster Prevention，2014，（accepted and in press）.（in Chinese）

［7］Grassberger P，I Procaccia.Measuring the Strangeness of Strange Attractors［J］.Phys D，1983，9：189－208.

［8］Gutenberg B，C F Richter.Frequency of Earthquakes in California［J］.Bull Seismol Soc Am，1944，34：185－188.

［9］Utsu T.A method for Determining the Value of bin a Formula logN ＝a－bMShowing the Magnitude Frequency for Earthquakes［J］.Geophys Bull Hokkaido Univ，1965，13：99－103.

［10］Chandrani Singh，Arun Singh，R K Chadha.Fractal and b－Value Mapping in Eastern Himalaya and Southern Tibet［J］.Bull Seismol Soc Am，2009，99（6）：3529－3533.

［11］Pacheco J F，C H Scholz，L R Sykes.Changes in Frequencysize Relationship From small to Large Earthquakes［J］.Na－ture.1992，355：71－73.

［12］Ulziibat M A Munkhsaikhan，D Mungunsuren.Seismicity and Seismotectonic of Mongolia［J］.2007，Presentation.

［13］Mori J，R E Abercrombie.Depth Dependence of Earthquake Frequency－magnitude Distributions in California：Implications for the Rupture Initiation［J］.J Geophys Res，1997，102：15，081－15，090.

［14］Gerstenberger M，S Wiemer，D Giardini.A Systematic Test of the Hypothesis that the b Value Varies with Depth in California［J］.Geophys Res Lett，2001，28：57－60.

［15］Lowrie W.Fundamentals of Geophysics［M］.Cambridge：Cambridge U Press，1997：354.

［16］Khan P K.Mapping of b－value Beneath the Shillong Plateau［J］.Gondwana Res，2005，8：271－276.

［17］Wyss M，D Schorlemmer，S Wiemer.Mapping Asperities by Minima of local Recurrence Time：San Jacinto－Elsinore Fault Zones［J］.J.Geophy Res，2000，105（B4）：7829－7844.

［18］Oncel A O，Main I，Alptekin O，Cowie P.Temporal Variations in the Fractal Properties of Seismicity in the North Anatolian Fault Zone Between 31°E and 41°E，Pure Appl［J］.Geophys，1996，147：147－159.

［19］Legrand D.Fractal Dimensions of Small，Intermediate，and Large Earthquakes［J］.Bull Seism Soc Am，2002，92：3318－3320.

［20］Wyss M，Sammis C G，Nadeau R M，et al.Fractal Dimension and B－value on Creeping and Locked Patches of the San－Andreas Fault Near Parkfield，California［J］.Bull Seism Soc Am，2004，94：410－421.

［21］Guo Z，Ogata Y.Correlation between Characteristic Parameters of Aftershock Distributions in Time Space，and Magnitude［J］.Geophys Res Lett，1995，22：993－996.