广义二次函数方程在模糊赋范空间上的Hyers-Ulam稳定性
2014-08-01崔哲男王彪赵顺实李林松
崔哲男,王彪,赵顺实,李林松*
(1.延吉市第二高级中学,吉林 延吉 133000; 2.延边大学理学院 数学系,吉林 延吉 133002)
0 引言
自从1940年Ulam[1]提出函数方程稳定性问题以来,许多学者对该问题进行了研究并取得丰硕的研究成果[2-4].近年来A.K.Mirmostafaee,J.M.Rassias,M.Mursaleen等在模糊赋范空间上研究了函数方程的稳定性,并取得了有意义的结果[5-8].2010年Mohammad[9]讨论了广义二次函数方程在一般赋范空间上的Hyers-Ulam稳定性,在此基础上本文进一步讨论了广义二次函数方程在模糊赋范空间上的Hyers-Ulam稳定性.
首先给出模糊范数空间上的一些基本概念[10].
定义1设X是实线性空间,若函数N∶X×R→[0,1]满足条件∀x,x′∈X,∀t,t′∈R,有:
(N1)∀t≤0,N(x,t)=0;
(N2)∀t>0,x=0 ⟺N(x,t)=1;

(N4)N(x+x′,t+t′)≥min {N(x,t),N(x′,t′)};
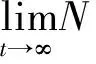
则称函数N为X上的模糊范数,(X,N)称为模糊赋范线性空间.

定义3设(X,N)是模糊赋范线性空间,{xn}⊂X.若∀ε>0,∀t>0,∃N∈N,使得∀n≥N,∀p>0,有N(xn+p-xn,t)>1-ε,则称{xn}为(X,N)中的Cauchy列.
显然,模糊赋范空间上的所有的收敛列都是Cauchy列.若模糊赋范空间上的每个Cauchy列都是收敛的,则称这个模糊赋范空间是完备的,完备的模糊赋范空间称为模糊Banach空间.
设X,Y是向量空间,函数f∶X→Y,k≥3.定义
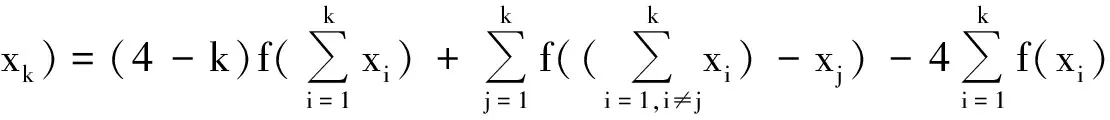
其中xi∈X,i=1,…,k.显然f(x)=x2满足
Df(x1,…,xk)=0,
(1)
所以称函数方程(1)为广义二次函数方程,满足广义二次函数方程的函数称为广义二次函数.
定理1[9]广义二次函数方程(1)等价于f(x+y)+f(x-y)=2f(x)+2f(y).
下面分两个部分给出广义二次函数方程的非一致广义模糊Hyers-Ulam稳定性定理及一致广义模糊Hyers-Ulam稳定性定理.
1 非一致广义模糊Hyers-Ulam定理


(2)
则存在唯一的二次映射Q∶X→Y满足方程(1)且
N(Q(x)-f(x),t)≥N′(φ(x,x,0,…,0),2(4-α)t),1<α<4,
(3)
N(Q(x)-f(x),t)≥N′(φ(x,x,0,…,0),2(α-4)t),α>4.
(4)
证明情况(1): 当1<α<4时.对∀n∈N,φ(2nx1,…,2nxk)=αnφ(x1,…,xk)成立,取xi=0,1≤i≤k,得φ(0,0,…,0)=αiφ(0,0,…,0)=αnφ(0,0,…,0),所以
φ(0,0,…,0)=0.
(5)
在(2)式中取xi=0,1≤i≤k,再由(5)式得N(4(1-k)f(0),t)≥N′(0,t),所以由(N2)得
f(0)=0.
(6)
在(2)式中取x1=x,x2=x,xi=0,3≤i≤k,再由(6)式得N(2f(2x)-8f(x),t)≥N′(φ(x,x,0,…,0),t),所以由(N3)得

(7)
将(7)式中x换成2ix,再由(N3)得

(8)
在(8)式中将t换成αit,再由(N4)得

(9)
在(9)式中将x换成2mx,再由(N3)得

(10)

(11)

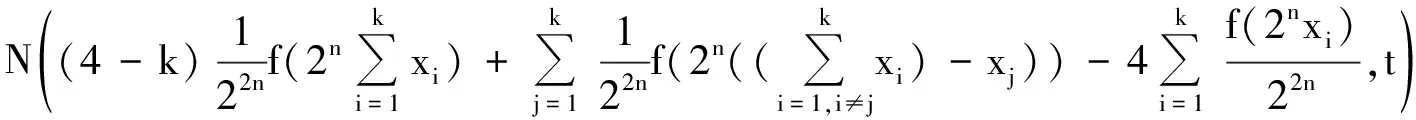

(12)
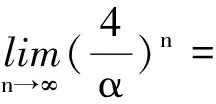
下证唯一性.假设存在另一个二次映射Q′∶X→Y且满足(3)式,则∀n∈N,有Q(2nx)=22nQ(x),Q′(2nx)=22nQ′(x).因此有

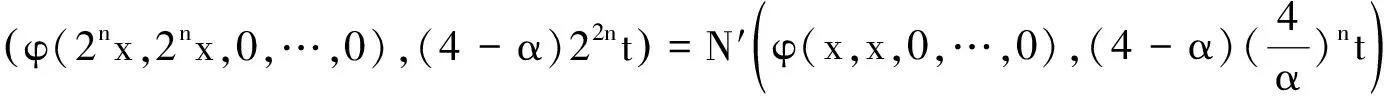
令n→∞,则∀t>0,可得N(Q(x)-Q′(x),t)=1,因此Q(x)=Q′(x).
情况(2): 当α>4时,在(7)式中用2-nx代替x,则有

同情况(1)的方法类似可得
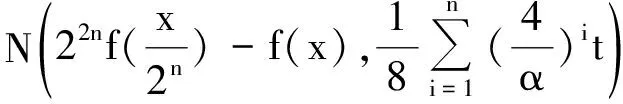
(13)
2 一致广义模糊Hyers-Ulam定理
定理3设X是线性空间,(Y,N)是模糊Banach空间,函数φ∶Xk→[0,+∞)对所有的x1,x2,…,xk∈X,满足

(14)
若函数f∶X→Y是关于函数φ模糊范数一致逼近广义二次函数,即
(15)


(16)
证明由(15)式,∀ε>0,∃T>0,∀t≥T,对所有的xi∈X,1≤i≤k,有
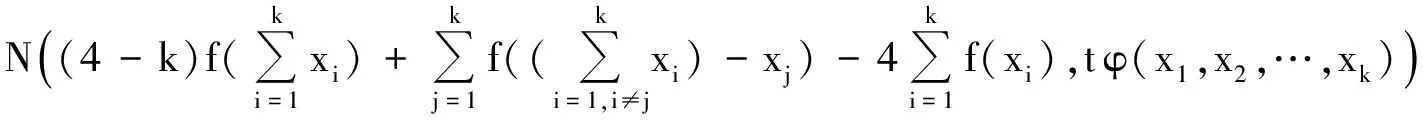
(17)
在(17)式中取xi=0,1≤i≤k,得
N(4(1-k)f(0),t φ(0,…,0))≥1-ε.
(18)
在(17)式中取x1=x2=x,xi=0,3≤i≤k,得
N(2f(2x)-8f(x)-2(2k-5)f(0),t φ(x,x,0,…,0))≥1-ε.
(19)
由(18)式和(19)式,再结合(N4)得

(20)
在(20)式中将x换成2nx,再结合(N4)得
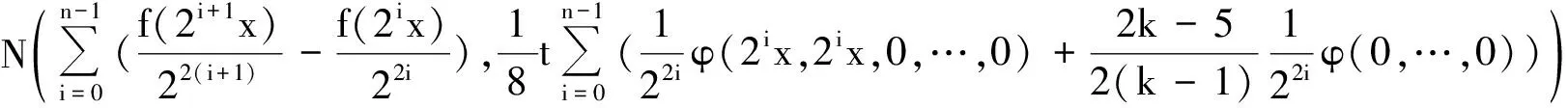
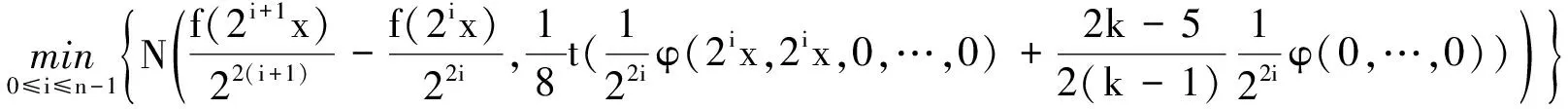
(21)
在(21)式中取t=T,n=p,将x换成2nx,则对所有的整数n≥0,p>0,有

(22)


(23)
因此有
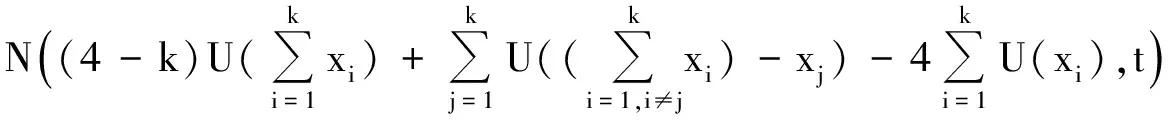
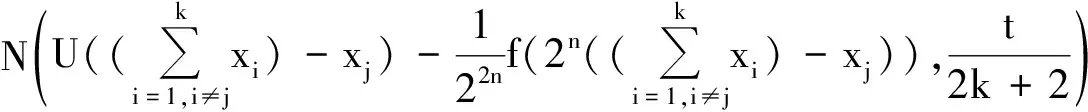

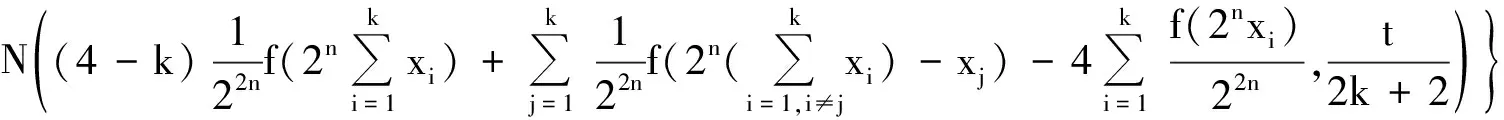


(24)
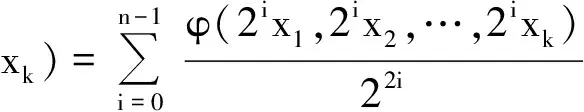


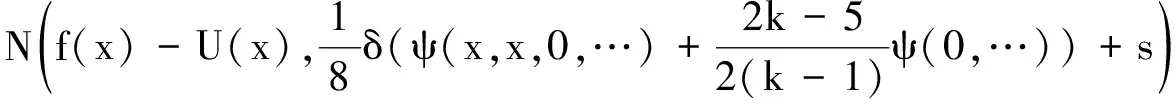
再令s→0即得

参考文献:
[1]Ulam S M. Problems in Modern Mathematics[M]. New York:Interscience Pubisher,1960.

[3]Rassias Th M. On the stability of the linear mapping in Banach spaces[J]. Proc Amer Math Soc,1978,72:297-300.
[4]Jung S M. Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis[M]. Florida: Hadronic Press,2001.
[5]Xu T Z,Rassias J M,Xu W X. A fixed point approach to the stability of a general mixed additive-cubic functional equation in quasi fuzzy normed spaces[J]. International Journal of Physical Sciences,2011,6:313-324.
[6]Javadi S,Rassias J M. Stability of general cubic mapping in fuzzy normed spaces[J]. An St Univ Ovidius,Constanta,2012,20(1):129-150.
[7]Mirmostafaee A K. A fixed point approach to almost quadratic mapping in quasi fuzzy normed spaces[J]. Fuzzy Set Syst,2009,160:1653-1662.
[8]Mursaleen M,Khursheed J A. Stability results in intuitionistic fuzzy normed spaces of a cubic functional equation[J]. Appl Math Inf Sci,2013,7(5):1677-1684.
[9]Mohammad J,Rahele Sh. On solution and Hyeres-Ulam-Rassias stability of a generalized quadratic equation[J]. International Journal of Nonlinear Science,2010,10(2):231-237.
[10]Bag T,Samanta S K. Finite dimensional fuzzy normed linear spaces[J]. The Journal of Fuzzy Mathematics,2003,11(3):687-705.
[11]Ulom S M. Problems in Modern Mathematics[M]. New York: Wiley,1964.
