冶金企业内部铁路网络区域划分研究

陈建强，张 昱，李春明

（1. 中铁第四勘察设计院集团有限公司 通号处， 武汉 430063；2. 铁道第三勘察设计院集团有限公司，天津 300142；3. 中铁第五勘察设计院集团有限公司，北京 102600）

冶金企业内部铁路网络区域划分研究

陈建强1，张 昱2，李春明3

（1. 中铁第四勘察设计院集团有限公司 通号处， 武汉 430063；2. 铁道第三勘察设计院集团有限公司，天津 300142；3. 中铁第五勘察设计院集团有限公司，北京 102600）

针对冶金企业内部的铁路线路呈网状分布的特点，提出一种基于共邻点矩阵与复合度函数、综合考虑划分子区域所需列车控制防护能力的线路网区域划分方法，并应用该划分方法对某钢厂企业的铁路线路网进行了区域划分，该划分结果有效地指导了区域控制系统控制范围的设计与规划。

冶金企业；内部铁路线路网；区域划分；共邻点矩阵；复合度函数；区域控制能力

铁路运输是冶金企业生产的动脉，列车运行控制系统是铁路运输的神经中枢，区域安全控制系统（RSCS ，Regional Security Control System）作为列控系统的核心部分，是实现列车安全高效运行最终执行者。在冶金企业内部，为了满足企业内部物料运输准时性要求，列车的接发车作业和机车的取送作业等交叉同时进行，整体铁路运输十分繁忙[1]，若整个厂区铁路运输只设置单个RSCS，则其所要控制的列车数将以百计，同时需要处理的数据量十分庞大，逻辑关系极为复杂，考虑到被自动控制的列车的登录或注销需尽快被响应，从而及时获得行车凭证以确认其安全的运行，最终完成相应的运输任务，因此单个系统难以做到。另外，一旦单个系统发生故障，将导致整个铁路运输系统降级进入人工控制模式，极大地降低运输效率，所以应对冶金企业内部的整个铁路网络进行划分，由多个系统分别控制。而合理的重叠划分还可对重叠区域实现冗余控制，当重叠区的某个控制子系统发生故障时，可以由该重叠区上的其他子系统控制，进而提高了重叠区安全防护的可靠性。综上所述，合理安排每个RSCS的控制范围，以实现其控制能力的最大化并获得最佳的控制效果，对于实现冶金企业内部铁路运输的自动化控制具有十分重要的意义[2]。

由于冶金企业内部的铁路线具有网状分布的特点，若以冶金企业内部各个生产车间内的各个停车点、炼铁高炉区各个高炉停车位、各个厂内功能编组站和联合编组站为顶点，各个顶点之间的铁路线为连线边构建网络模型[3]，由于各个顶点之间可能同时存在多条铁路线相连线路，线路网各个顶点之间的单条连线就具有了权重，且可双向行车，因此线路网是一个无向有权的网络。所以，合理安排每个RSCS的控制范围问题就成了如何对此线路网进行区域划分的问题。

对于复杂网络区域划分的相关研究大体包含计算科学中的图形分割[4～5]和社会科学中的层次聚类[6～8]，以及由Donetti和Newman等人提出结合二者优缺点，引入一种衡量顶点间的相似性标准模块度的结合谱分析和凝聚算法特点的算法[10～12]，并推广到加权网络中。文献[13]、[14]受模块度思想的启发，以顶点与顶点之间所拥有的共邻点数作为区域划分的衡量标准，由此将基于共邻点矩阵和复合度函数的算法推广到加权网络中，结果明显优于Newman等人基于模块度的多区域划分算法和其他的区域划分算法。因此，参考文献[14]，本文定义一个共邻点矩阵和一个复合度函数，综合考虑划分子区域所需列车控制防护能力，提出一种针对企业内部的铁路网络进行区域划分方法，最后利用这种划分方法对某大型钢厂铁路网进行区域划分，分析划分结果的有效性并据此划分结果设计RSCS的控制区域范围，控制结果表明所述划分方法有效可行。

1 基于共邻点矩阵与复合度函数的线路网区域划分算法

区域划分问题可描述为一个并行计算的问题：假设有n个来自各个顶点的运输任务需由x个RSCS完成，每个任务不一定和其他任务有直接关联。所有的运输任务之间的关联模式由整个厂内的铁路网来表示，如图1所示，网络中每一个顶点对应一个运输任务，而每条边就连接了一对需要直接联络的关系。区域划分的问题就是如何分配这n个顶点（包含运输任务）到这x个RSCS上，使得每个RSCS处理的运输任务数近似相等，且各个RSCS之间连接的边数最少，从而使各个RSCS之间的通信量最小（也就是发生区域交接的次数最少，因为区域交接会在某种程度上影响运输效率）。

当企业内部的铁路网络的规模很大时，找到一个使各个区域安全控制系统之间连接的边数最少，从而使各个区域安全控制系统之间的通信量最小的区域划分问题的精确解是一个NP难问题，因此本文采用试探性算法以期求得满意解。

1.1 带有权重的联结矩阵及其共邻点矩阵

为便于描述，将上述线路网G抽象为一个由顶点集V(G)={1, 2,…, i,}和边E(G)={(i1, j1), (i2, j2), …}组成的图，若(i, j)=(j, i)，则G为无向图，否则为有向图[15]。若定义：

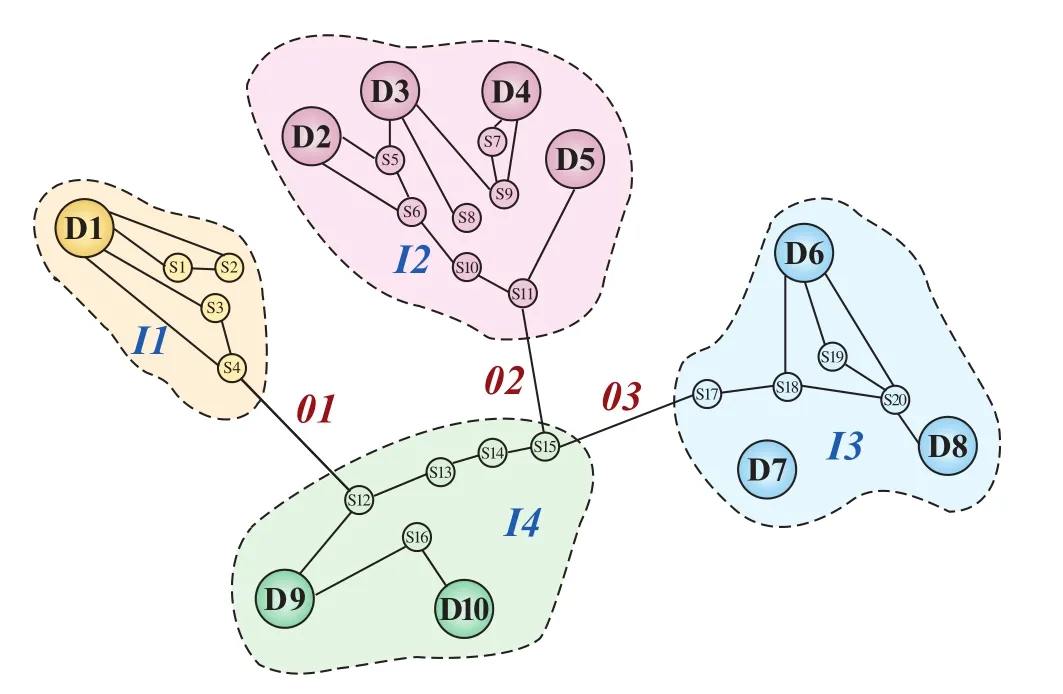
图1 具有区域结构的企业内部铁路线路网络示意图

则联结矩阵A={aij}表示图G中顶点之间的连接关系，由于上节所构建的线路网是一个无向有权的网络，因此 是一个非零元素代表边的权重的对称的0-1矩阵[13～14]，也就是把顶点之间有n条边相连看作是权重为 的1条边联结着2个顶点，如图2（b）所示为某简易加权线路网的示意。若定义共邻点矩阵 H，则其各个元素可表示为[14]：

由于只有当第i个顶点和第j个顶点有边相连时，aikakj=1，因此Hij表示顶点i和顶点j共有相同邻点的数目。如图2（a）中，顶点IV就是顶点I与顶点II的一个共邻点，其共邻点矩阵H的计算如图2（b）所示。

图2 简易区域内网络及其共邻点矩阵

而图2（c）中，由于顶点I通过顶点IV到达顶点II的路径有6条，因此可以认为顶点I与顶点II拥有共邻点（即顶点IV）的数量为6，其共邻点矩阵H的计算如图2（d）所示，其中非零元素代表边的权重。

1.2 复合度函数

由于基于共邻点矩阵区域划分的算法是通过使区域内部的顶点对之间拥有尽可能多的共邻点，因此需要定义一个复合度函数，以度量共邻点的多少，继而通过寻找一种区域划分使复合度函数最大，获得算法搜索的终止条件。结合公式（1）和公式（2），参照文献[11～12]中对随机相连的网络中两个顶点有边相连的概率表示，以di和dj分别表示顶点i和j的度，didj/n表示当网络随机相连接时顶点对之间拥有的共邻点的数目，复合度函数的定义如下：

其中∏ij表示顶点i和j的区域认定函数，且

可见，Ψ体现了区域内部顶点对之间拥有的共邻点的数目与在随机网络相连的情况下的数目的差，也就是当Ψ＜0时，网络中将不存在区域结构。

1.3 基于共邻点矩阵和复合度函数的线路网的区域划分算法

首先定义一个标示向量Θ，其各个元素为：

则有：

因此，复合度函数为：

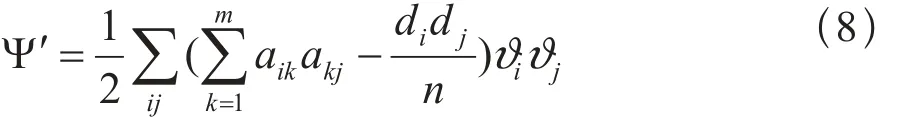
若定义对称矩阵X为复合度矩阵：

则可将式（8）写成：

由于X为实对称矩阵，当n个特征值互异时，利用其标准正交基η1, η2,…,ηn表示向量X，有写成δi=ηT

iX代入式（10），可得到：

其中：ζi指X对应的特征向量ηi的特征值。

若假设ζ1≥ζ2≥…≥ζn，通过选择适当的δi使式（11）中的最大特征值的那一项在最大化Ψ'时发挥主要作用。在一般的谱分析中，若标示向量ϑ的选取无约束，则可选其正比于矩阵X的主特征向量η1（表示最大特征值对应的特征向量），而式（5）中对ϑ具有限定，因此ϑ不能平行于η1，故只能选择ϑ尽可能平行于η1，获得较好的次优解，也就是令：

其中，ηi1表示主特征向量η1中的第i个元素。

上述过程可以总结为：首先求得复合度函数最大特征值的主特征向量，然后根据主特征向量中的元素符号把网络划分为两个区域。若复合度函数的最大特增方程为m重根，需要对其对应的m 个特征向量Schmidt正交化，然后根据m个正交化后的特征向量中的元素符号把网络划分为两个区域，共有m种不同的结果。

至此，上述方法可将线路网划分为两个区域，然而这往往是不够的。为了继续进行划分，可以先假设其中一个区域为ξ，且该区域包含nξ个顶点，将上述划分方法继续用在区域ξ，继续将其划分为更小的区域。但是当一个网络被划分为两个区域之时，由于已删去了连接这两个区域的边，导致区域内部顶点的度发生了变化。为此，这里给出继续划分子区域ξ的过程中产生的复合度函数ψ的增量∆Ψ计算公式：

其中：

重新定义针对区域 中顶点的复合度矩阵：

从而式（15）可以写成：

由于式（16）与式（10）的形式相同，因而可与上述划分两个区域时使Ψ最大化的方法使∆Ψ最大化来划分区域ξ。文献[13]根据复合度函数Ψ是否继续增加作为是否终止划分的条件，即当∆Ψ≤0（说明整个网络经过划分后各个子区域已经不再存在区域结构特征）时，终止划分。但对于本文，如果只是参考上述终止条件将使划分的区域范围过小，造成RSCS控制能力的浪费，进而抬高了造价与成本。同时由于重根的存在，上述划分方法可能得出多种划分方案，本质上，这些划分结果只是考虑了区域之间交接最少的目标，而未考虑RSCS控制能力的利用。因此，下文将参考系统设计的相关知识，结合实际，给出另一个综合考虑RSCS控制能力区域划分的终止条件。

1.4 各个控制系统的控制能力的计算及其能力边界

在冶金企业内部的线路网的相关运输中，各个顶点之间因为运输需求的存在而联结在一起，这些运输关系包括接发车和取送车作业，前者主要对应于铁路局列车的运输作业，后者则主要是厂内的生产运输。由于企业内部的连续不间断生产的特点，在一定的周期内，各个生产车间对所需物资的运输需求相对稳定，因此其铁路线路网上各个顶点之间所运输的物资种类和运量相对比较固定，这使得对各个顶点的运输需求的确定提供给了可能，因而可以确定出各个顶点之间运输的繁忙程度，进一步确定子区域所需的RSCS控制能力。考虑到所设计的RSCS的控制能力一般考虑单个系统同时能处理的可能同时存在：

（1）已设置的路径数R；（2）已激活的TSLA（临时限速服务区域）个数TSLA；（3）已激活的紧急区域个数EB；（4）控制的道岔组的范围l道岔；（5）需要装或卸的装卸区个数FH；（6）登录的列车数量V。

计算所划分的子区域所包含的上述R、TSLA、EB、l道岔、FH和V的值，由于在特殊情况下，如果发生区间列车堵塞现象，这时列车运行速度已经下降，当RSCS控制的列车数量超过RSCS容量时，新列车将无法呼叫RSCS以取得行车凭证正常运行，因此，对于上述各个数目的值应设定一定的冗余量∂，各个冗余值∂FH和∂V根据各个区域的线路特点和生产设备商所提供的RSCS设备性能进一步确定，本文分别取表1中的值。

表1 各个参量的冗余值

故所划分的子区域需满足式（17）成立：

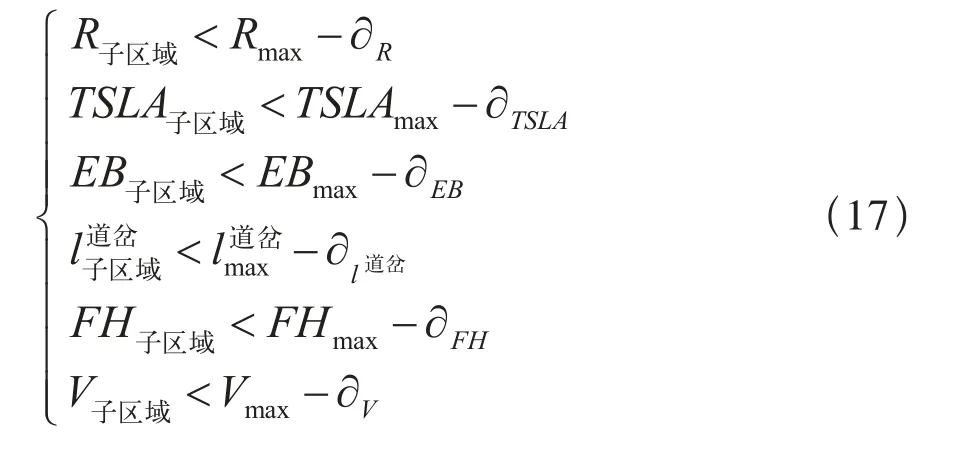
其中：下标为“子区域”分别表示划分所得的子区域所包含的R、TSLA、EB、l道岔、FH和V的值，下标为“max”表示单个RSCS所能监控的 R、TSLA、EB、l道岔、FH和V的最大值，该值由设备生产商提供。式（17）即为RSCS的控制能力边界。R、TSLA、EB、l道岔、FH和V值的计算方法如下：

（1）对于R，由于取消了轨道电路，不存在严格的路径概念，因此计算路径R的数量以所划分的子区域内所可能完成的运输任务所需要安排的路径的最大值，这个值可通过机车车辆控制中心获得，其根据调度任务综合计算求得；

（2）对于TSLA，根据整个企业生产厂区的全局地图上的铁路线路数据，当子区域划分出来后，只需在相应的范围内搜索即可获得；

（3）对于EB和FH的计算方法同（2）；

（4）对于l道岔，根据整个企业生产厂区的全局地图上的铁路线路数据，确认所划分的子区域最大范围不超过设定范围；

（5）对于V，包括区间列车数量V区间、站内停车数量V站内以及RSCS控制分界口列车数量V分界口，即：

其各部分求解方法如下。

a.区间列车数量V区间

由于冶金企业内部的铁路运输基本都是货物运输，且运送不同货物的列车具有不同的等级，在同一区间上采用的运行速度也不尽相同，因此其运行图呈现非平行的特点，参考文献[16]，将冶金企业内部各种类型的列车定义成3个不同等级，并定义其相应的扣除系数（即在运行图上铺画列车时需要从平行运行图上扣除的列车对数或列数），某钢厂采用的扣除系数如表2所示[17]：

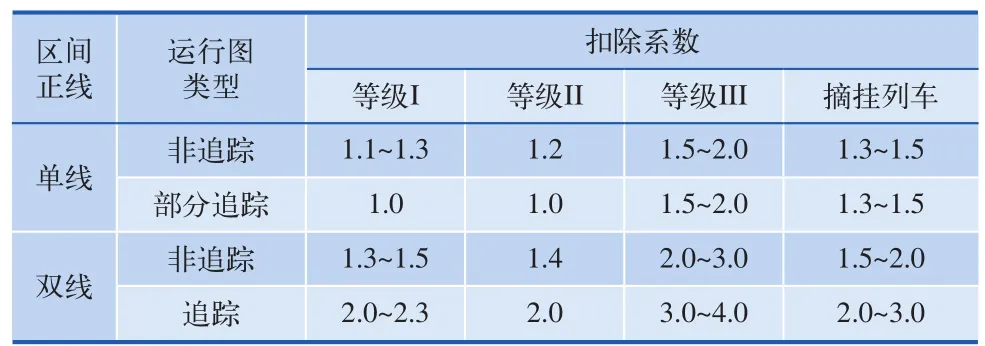
表2 扣除系数表

非平行运行图的通过能力η非的计算公式为[16]：

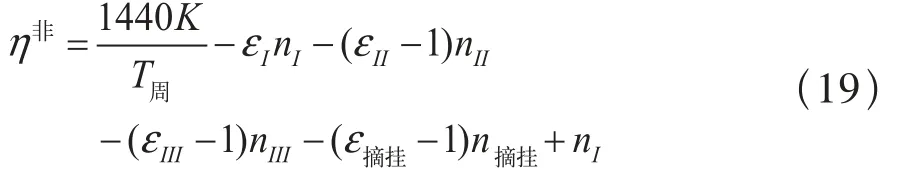
其中：K指一个T周中所包含的列车对数或列数，T周指平行运行图上任何一个区段的列车运行线以同样的铺画方式所排列的一组列车占用区间的时间，详见参考文献[16]，这里不再赘述；εI～εIII分别指等级为I～III的列车扣除系数；ε摘挂指摘挂列车扣除系数； nI～nIII分别代表铺画在非平行运行图上的等级为I～III的列车对数或列数； n摘挂代表铺画在非平行运行图上的摘挂列车对数或列数。

根据式（19）和表2的扣除系数，结合企业内部已有的铁路运输运行图，可求得区间列车数量：

b.车站停车数量V站内

在计算区间列车数量V区间时，实际已经考虑了车站正线股道上的列车，因此在计算车站停车数量V站内时，只需要计算到发线的停车数，即待发列车数和调度列车数，这两个数可分别由到发线股道数（每股到发线为1列）和车站的编组能力（一般每3条调车线有1辆摘挂机车作业）取其总和的最大值求得。

c.分界口列车数量V分界口

冶金企业内RSCS的区间管辖范围内与外部一般有多处分界口，若n个接口处为双线则取2列，m个接口处为单线取1列，共有车数2n+m列。

1.5 区域划分算法

综上，对于冶金企业内部铁路线路网区域划分的最终算法如下：

步骤1：对冶金企业内部的铁路线路网G中的顶点进行相应的编号，求解G的复合度矩阵ΨG；

步骤2：求解复合度矩阵ΨG的最大特征值，若最大特征值不存在重根，转步骤4；

步骤3：若最大特征值存在m重根，依次取其中一个重根，转步骤4，并存储每一种划分结果；

步骤4：根据Lanczos方法求解最大特征值所对应的主特征向量，根据主特征向量的元素符号把铁路线路网划分为两个区域；

步骤5：根据上述方法及公式计算所有划分结果中每个子区域的R、TSLA、EB、l道岔、FH和V的值，判定式（17）是否满足，若满足，则终止划分，比较各个划分结果，选取各个R、TSLA、EB、l道岔、FH和V的值最为接近的一组为最终解，否则继续下一步；

步骤6：对于每一个子区域，用式（16）来代替式（10），重复步骤2；

步骤7：断定Ψ是否继续增加，即若∆Ψ≤0成立，则终止划分，否则转到步骤2。

由于线路网具有较明显的区域特征，对于顶点数为n，边数为m的网络，步骤2中线路网的复合度矩阵是一个稀疏矩阵，其主特征值λ2能很快从其他特征值中分离出来，因此步骤4中用Lanczos方法计算其主特征向量的时间复杂度约为m/(λ3–λ2)；而步骤5计算过程的时间复杂度为m+n，因此整体算法时间复杂度约为O(n(n+m))。

2 应用示例

本文根据上述划分方法，对某钢厂企业内部的铁路线路网进行区域划分，并将自主研制的针对企业内部铁路运输区域控制系统软件在自主构建的冶金企业仿真环境中布置安排，通过其运行结果来验证本文所提划分方法的有效性。图3为某实际钢厂的铁路运输情况。

图3 某钢厂的铁路运输状况

其内部共有原料站1个，中心库1个，机务段2个，热电站2个，连铸连轧厂3个，线材厂2个，中板厂2个，炼钢厂4个，炼铁厂3个，轧钢厂4个，工厂站4个，综合料场2个，渣池3个，综合利用加工厂1个，酸洗镀锌厂1个，锅炉房2个，高炉5个，原料房2个，焦化站1个，焦化厂3个，烧结厂3个，其相应的路径数R为513条，TSR（临时限速服务器）个数为126个，紧急区域个数EB为234，道岔组的范围l道岔为21 km以内，装卸区个数FH为147个，车数量V为287列。上述铁路线路网的区域划分结果如图4所示。

图4 某钢厂的铁路线路网区域划分结果

图4 中，3次划分把整个线路网划分为4个区域：

区域1中：R=123条；TSR =34个；EB =67个；l道岔＜12 km；FH=36个；V=94列。

区域2中：R=166条；TSR =46个；EB =76个；l道岔＜14 km；FH=56个；V=57列。

区域3中：R=94条；TSR=19个；EB=43个；l道岔＜9 km；FH=23个；FH=63列。

区域4中：R=130条；TSR=27个；EB =48个；l道岔＜16 km；FH=32个；V=73列。

根据该划分结果设计布置区域控制系统的控制范围，应用结果不仅实现了交接区域路径最少，交界区的切换次数最少（相邻区域监控系统之间的交换数据量最少），简化区域交接过程的复杂性，提高了安全可靠度，同时满足每个RSCS的控制范围在其能力之内，且不至于太小（当小于其控制范围内的列车在舒适运行状态下的常用制动距离时，将导致相邻两个区域监控系统跨区呼唤而引起控制权的竞争，最终导致诸如“幽灵列车”出现等故障的发生，引发危险事故），各个RSCS的控制能力合理分布。

3 结束语

本文针对冶金企业内部的铁路线路呈网状分布的特点，构建线路网络模型，参考复杂网络划分的相关理论，提出一种基于共邻点矩阵与复合度函数、综合考虑划分子区域所需列车控制防护能力的线路网区域划分方法，并应用该划分方法对某钢厂企业的铁路线路网进行了区域划分，根据该划分结果设计布置区域控制系统的控制范围。应用结果表明，本文所提出的划分方法能有效地指导区域控制系统对列车控制范围的设计与规划，对于有效防护列车的安全运行，实现铁路运输的自动化具有实际指导意义。

[1] 李鹏云，牛清梅，崔新金，等．浅谈冶金企业铁路运输的发展[J]．安阳师范学院学报，2003（2）：87-89.

[2] 苑志斌，安海轩，魏启宁.2013-2017年中国冶金工业投资分析及前景预测报告[J] .中投顾问，2013（8）：1-7.

[3] 何 诚.中国铁路网的复杂网络性质研究[D].广州：中山大学，2007：38-60.

[4] Garey M R, Johnson D S. Computers and Intractability:A Guide to the Theory of NP-Completeness[M]. San Francisco: Freeman Publishers, 1979.

[5] Kernighan B W, Lin S. An efficient heuristic procedure for portioning graphs[J]. Bell System Technical Journal, 1970（49）：291-307.

[6] Scott J. Social Network Analysis: A Handbook[M]. Sage Publications, London, 2000.

[7] Fiedler M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal, 1973, 23 (98): 298-305.

[8] Pothen A, Simon H, Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J].SIAM Journal on Matrix Analysis and Applications. 1990, 11(3): 430-452.

[9] Girvan M, Newman M E J. Community structure in social and biological networks[J]. PNAS, 2001, 99(12): 7821-7826.

[10] Donetti L,Munoz M A. Detecting network communities: A new systematic and efficient algorithm[J]. Stat. Mech. Thior. Exp, 2004(10): P10012.

[11] Newman M E J. Analysis of weighted networks[J]. Phys. Rev. E, 2004, 70(5): 056131.

[12] Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review. E, 2006, 74(3): 036104.

[13] 郭崇慧，张 娜.基于共邻矩阵的复杂网络社区结构划分方法[J].系统工程理论与实践，2010，30（6）： 1077-1084.

[14] 张 娜.复杂网络社区结构划分算法研究[D]. 大连：大连理工大学，2009：13-24.

[15] 汪小帆，李 翔，陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社，2006：17-25，46-54.

[16] 高继祥.铁路信号运行基础[M]. 北京：中国铁道出版社，2008：80-84.

[17] 贾忠孝.厂矿铁路运输组织[M]. 北京：冶金工业出版社，1994：107-112.

责任编辑 方 圆

Regional division of railway network for metallurgical enterprises

CHEN Jianqiang1, ZHANG Yu2, LI Chunming3
( 1. Communication & Signal Design & Research Dept., China Railway Siyuan Survey and Design Group Co., LTD., Wuhan 430063, China; 2. The Third Railway Survey and Design Institute Group Corporation, Tianjin 300142, China; 3. China Railway Fifth Survey and Design Institute Group Co., LTD., Beijing 102600, China )

metallurgical enterprises; railway network; regional division; common adjacency matrix; combined degree function; regional control capability

This paper focused on the railway net areal distribution in metallurgical enterprise, proposed a network partition method which was based on common adjacency matrix and combined degree function, considerated the required train control protection ability of each sub-area. The applications of this division method in a metallurgical enterprise showed effective feedback, guided the design and planning of the range of regional control systems.

2014-05-16

陈建强，助理工程师；张昱，助理工程师。

F530.32∶TP39

A

1005-8451（2014）11-0009-07