冷却塔对带钢抖动的有限元分析*
2014-07-31杨安东庞宇江
王 彪, 柏 兵, 杨安东,庞宇江
(安徽工业大学 机械工程学院, 安徽 马鞍山 243032)
冷却塔对带钢抖动的有限元分析*
王 彪, 柏 兵, 杨安东,庞宇江
(安徽工业大学 机械工程学院, 安徽 马鞍山 243032)
基于冷却塔对连续热镀锌带钢抖动影响的研究,通过采用有限元分析软件I-DEAS 对冷却塔整体进行了建模和固有模态计算,并利用现场已有的测试数据进行对比分析来验证计算结果的准确性。在此基础上,研究了塔顶的局部,对塔顶两层单独建立了有限元模型,并对其进行了有限元计算,结果表明塔顶两层在第七阶模态时出现了弯曲振型,此振型对塔顶辊影响最大。最后,针对塔顶两层提出了两种改进方案,通过对模态和动态响应的计算分析比较得出方案的可行性。
冷却塔;有限元;模态;动态响应
1 前 言
冷却塔主体结构较简单,属于大尺度空间桁架结构,各层楼板框架和楼梯是由无数纵横交错、规格形状不同的型钢焊接或栓结而成的复杂小尺度平面桁架。冷却塔的塔顶辊是带钢上行段的一个支撑段,由于塔顶辊安装在冷却塔顶层,冷却塔塔顶局部的动力学特性会影响到塔顶辊进而影响到带钢的抖动,因此冷却塔对带钢抖动的影响至关重要。笔者通过对塔上设备和构件的简化,在有限元软件I-DEAS[1]上建立了冷却塔的有限元模型,在此基础上,进一步分析塔顶局部对带钢抖动的影响,为合理设计塔的修正方案提供依据。
2 冷却塔整体有限元模型的建立和论证
冷却塔属于空间桁架结构,宜采用梁单元[2]建立有限元模型,经过对塔上设备和构件的简化,可以得到冷却塔的有限元模型,如图1所示。
冷却塔整体固有模态分析的计算结果如图2~7所示。

图1 冷却塔的有限元模型
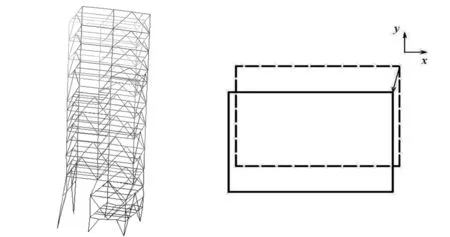
图2 冷却塔一阶阵型 图3 一阶振型时的冷却塔顶层振动示意图

图4 冷却塔二阶阵型 图5 二阶振型时的冷却塔顶层振动示意图

图6 冷却塔三阶阵型 图7 三阶振型时的冷却塔顶层振动示意图
计算结果分析如下:
(1) 第一阶振型:冷却塔作类似悬臂梁的一阶弯曲摆动,在x向和y向都有分量,但y向分量比x向大得多,x向弯曲振动时的冷却塔顶层振动如图3所示。
(2) 第二阶振型:冷却塔作类似悬臂梁的一阶弯曲摆动,在x向和y向都有分量,这与第一阶模态类似,但x向分量比y向大得多,y向弯曲振动时的冷却塔顶层振动如图5所示。
(3) 第三阶振型:冷却塔绕z轴扭摆振动,扭转振动时的冷却塔顶层振动示意图如图7所示。
冷却塔的整体固有频率如表1所列。
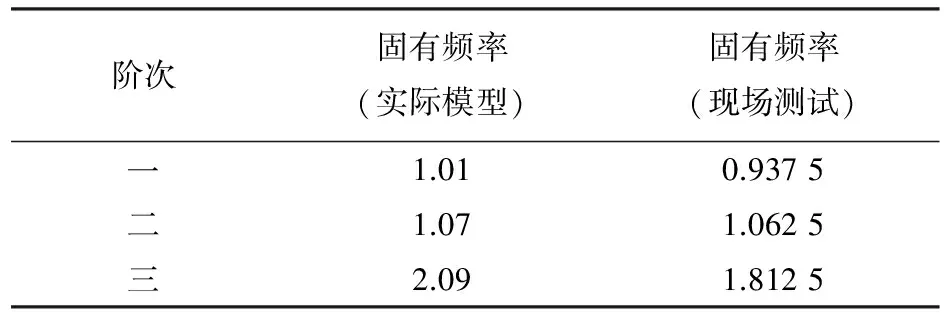
表1 冷却塔固有频率 /Hz
从表1中可以看出,实际模型的有限元计算结果与现场测试的数据完全吻合,可以认为已经论证了之前所建立的有限元模型的准确性。
3 塔顶局部分析
带钢离开锌锅垂直向上至冷却塔塔顶第一转向辊,其行程高达60多米。其间不但没有棍子托扶,而且还要经受气刀、冷却风箱等强大气流的喷吹,所以带钢在这段运行时一般抖动都相对比较严重。带钢不仅受横向载荷,而且还在纵向(轴向)受张力作用,故带钢抖动理论上属于“轴向运动薄板的纵横弯曲振动”问题。引起带钢抖动的因素可分为强迫振动[3](气刀处气流脉动、风箱气流脉动、两棍子垂直于带钢表面的支撑运动)和参数激励振动[4](带速变化、张力波动等)。
为了更详细更全面地研究塔顶辊及其支撑系统,在冷却塔塔有限元模型的基础上为冷却塔塔顶两层单独建立了有限元模型,对塔顶两层的局部动力学特性进行了有限元计算,计算结果表明:冷却塔在第七阶模态时图8出现了弯曲阵型,其相应的固有频率为5.437 614 4 Hz。在现场测试中,所求得得塔顶辊及其支撑子系统的固有频率就是该振型所对应着的固有频率。

图8 冷却塔第七阶阵型
4 修正方案的提出
为了改善塔顶局部动特性对带钢抖动的影响,提出两套塔顶两层局部设计的改进方案(如图9、10所示,图中圆圈为标记的改造新增结构,分别建立了有限元模型,并将其计算结果与“实际模型”进行了比较,期望从中能筛选出一个令人满意的方案。

图9 第一种方案实体图 图10 第二种方案实体图
4.1 局部修正方案的模态分析
第一种方案的局部模态,如图11、12所示,第二种方案的局部模态如图13、14所示。
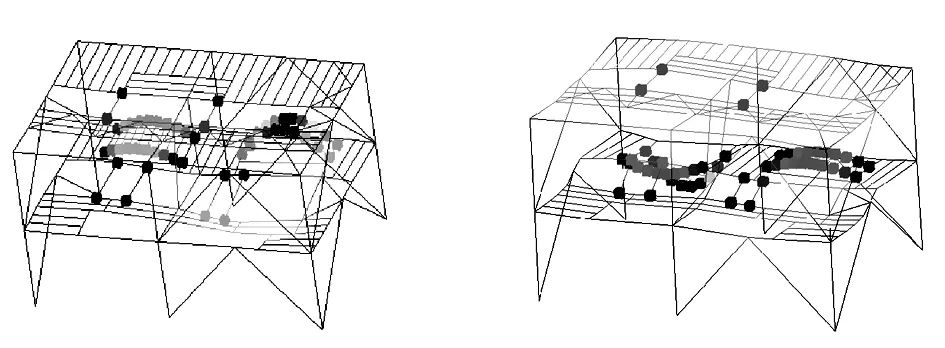
图11 第七阶振型频率6.381 419 Hz 图12 第八阶振型频率6.617 864 Hz

图13 第七阶振型 频率5.0153 26 Hz 图14 第八阶振型 频率6.172 766 Hz
从上述有限元计算结果可以看出,方案一和方案二第七阶和第八阶阵型均没有明显的顶层弯曲阵型,因此有改进的意义。
4.2 局部修正方案的动态响应分析
考虑到带钢的张力波动对冷却塔的影响,可以把张力波动作为外部激励,以此来计算冷却塔顶两层的动态响应。设张力为38 000 N,波动范围为10%,波动频率为4 Hz。实际模型的动态响应如图15、16所示。最大位移数值如表2所列。第一种方案的动态响应如图17、18所示,第二种方案的动态响应如图19、20所示。

图15 t=3.5 s时的峰值响应 图16 t=10.5 s时的谷值响应

表2 冷却塔顶两层的位移响应 /mm
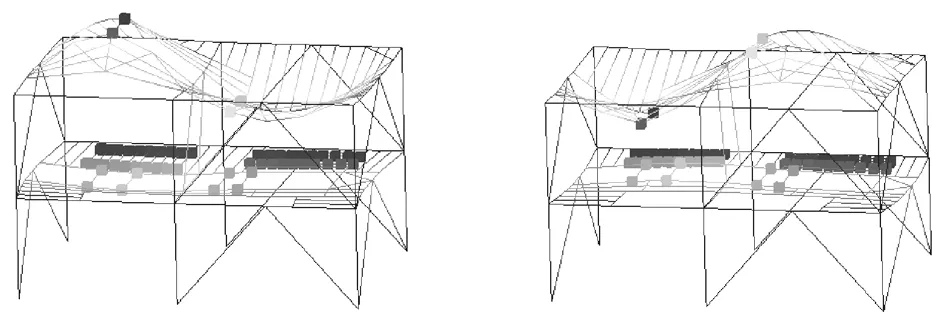
图17 t=3.5 s时的峰值响应 图18 t=10.5 s时的谷值响应

图19 t=3.5 s时的峰值响应 图20 t=10.5 s时的谷值响应
5 结 论
(1) 通过对塔顶两层的局部模态计算可知,对于修正前模型,其第七阶振型出现了顶层弯曲振型,该振型对塔顶辊的影响最大。现场测试的频率实际上就是该振型所对应的频率,测试结果与该振型所对应频率相接近,进一步验证了有限元的计算结果。因此有必要对塔顶层的结构进行改进。
(2) 有限元的计算结果还显示出,对于塔顶加强方案无论是方案一还是方案二,第八阶振型中均没有明显的顶层弯曲振型。因此有改进的意义。另外,从动态响应的最大位移值来考量,方案二的最大响应位移比方案一的大30%,似乎方案一从位移响应来判断更有效。
[1] 廖 东.I-DEAS实例教程——有限元分析[M].北京:北京理工大学出版社,2003.
[2] 杨建新,魏海燕.I-DEAS入门与提高[M].北京:清华大学出版社,2002.
[3] 程耀东,李培玉.机械振动学[M].杭州:浙江大学出版社,2005.
[4] 顾致平.非线性振动[M].北京:中国电力出版社,2012.
Finite Element Analysis of Strip Steel Jitter For Cooling Tower
WANG Biao, BAI Bing, YANG An-dong, PANG Yu-jiang
(SchoolofMechanicalEngineering,AnhuiUniversityofTechnology,MaanshanAnhui243032,China)
Based on the effects research of the cooling tower of continuous hot dip galvanized strip jitter, in this paper, by means of finite element analysis with software I-DEAS for cooling tower, the modeling and calculation of intrinsic mode has carried on and taking advantage of the existing test data, the accuracy of the calculation results were analyzed to verify. On this basis, the two layers of the tower are studied and finite element model is established, and the finite element calculation is done. The results show that the top two layers in the seventh order modal appears bending vibration and has also big impact. Finally, the improved scheme is given , the feasibility scheme of the modal and dynamic response is given by the calculation analysis and comparing.
cooling tower; finite element; modal; dynamic response
2013-11-10
王 彪(1962-),男,安徽马鞍山人,副教授,硕士, 主要从事工程力学和有限元等方面的研究工作。
TH14
A
1007-4414(2014)01-0030-03
