Texture Image Classif i cation Based on Gabor Wavelet

DENG Wei-bing,LI Hai-fei,SHI Ya-li,YANG Xiao-hui

(1.Institute ofAppliedMathematics,CollegeofMathematicsandInformationSciences,HenanUniversity,Kaifeng 475004,China;2.TheSeventhHighSchoolinZhengzhou,Zhengzhou 451200,China)

Texture Image Classif i cation Based on Gabor Wavelet

DENG Wei-bing1,LI Hai-fei1,SHI Ya-li2,YANG Xiao-hui1

(1.Institute ofAppliedMathematics,CollegeofMathematicsandInformationSciences,HenanUniversity,Kaifeng 475004,China;2.TheSeventhHighSchoolinZhengzhou,Zhengzhou 451200,China)

For a texture image,by recognizining the class of every pixel of the image,it can be partitioned into disjoint regions of uniform texture.This paper proposed a texture image classif i cation algorithm based on Gabor wavelet.In this algorithm,characteristic of every image is obtained through every pixel and its neighborhood of this image.And this algorithm can achieve the information transform between dif f erent sizes of neighborhood. Experiments on standard Brodatz texture image dataset show that our proposed algorithm can achieve good classif i cation rates.

texture image;Gabor wavelet;image classif i cation

§1.Introduction

Texture plays an important role in many applications such as surface inspection,sense classif i cation,and surface orientation.The objective of texture classif i cation is to assign an unknown sample image to one of a set of known texture classes.A successful classif i cation or segmentation requires an efficient description of image texture.A wide variety of texture feature extraction methods have been proposed in the computer vision and image processing literature in order to characterize dif f erent texture patterns[13].And also more novel techniques for extracting texture feature have been presented in recent years[47].

Texture classif i cation[89]process involves two phases:the learning phase and the recognition phase.In the learning phase,the aim is to build a model for the texture content of each textureclass present in the training data,which generally comprises of images with known class labels. The content of the training images are captured with the chosen texture analysis method,which yields a set of textural features for each image.In the recognition phase,pixel-based texture classif i cation[3]is a combination of the two promising techniques,and serves to determine the class to which every pixel of an input image belongs.Obviously,this method leads to segmentation of images.

This paper is based on the technique proposed by J Melendez et al[10].Previous work in[10] provided a technique that multi-sized evaluation windows are utilized by following a top-down approach for the classif i cation.Then a K-nearest neighbors(KNN)classif i er was used to assign a label to every pixel within the classif i ed image by fusing the information from multi-sized evaluation windows.Since Gabor f i lters optimally capture both local orientation and frequency information from an image,they are suitable for extracting texture information from images and applied in our paper.Prototypes selection is necessary because of the nature of the pixel-based texture classif i cation,which could save the computation time and memory usage.The current paper presents an improved version of pixel-based classif i cation scheme.The main dif f erences are(a)the prototypes are selected by applying weighted kernel k-means clustering algorithm[11]to yield a lower number of training sets;(b)in the process of top-down approach,we apply a new method of marking the unknown pixels;(c)pixel-level classif i cation is performed by SVM(Support Vector Machine)classif i er[12],which leads to better classif i cation results.

In remainder of this paper,we address Gabor feature extraction techniques in Section 2;then we discuss prototype selection methods in Section;Section 4 presents our proposed pixel-based texture classif i cation algorithm;Section 5 gives the experimental results;f i nally in Section 6, we draw our conclusions of our investigations in this paper.

§2.Gabor Feature Extraction

2.1Gabor Transform

The visual perception of human is the objective that the computers are visual studing and tracting.Two 2-D Gabor function is def i ned as

Recent studies have shown that when 2-D Gabor f i lter is extracting low level visual feature, that is similar with the respond of image signal,this open up a new research direction for image recognition.

In L2domain,a function f(t)can be used to describe an analog signal with limited energy, and its Fourier transform is def i ned as

One of the weaknesses of Fourier transform lies in that it can not handle the signal in both time and frequency domains simultaneously.Nevertheless,for most practical problems,it isoften desired to know the local characteristic or the mutation of the signal.For example,the position of gray mutation is essential in identifying boundaries of objects in an image.

In order to study the characteristics of local signal frequency,D Gabor presented windowed Fourier transform,which is also called Gabor transform[13].Gabor transform plays a signif i cant role in unstable signal analysis,and it is widely used in image processing,pattern recognition, as well as computer vision.As we know,Fourier transform takes the unstable signal as a superposition of a series of short-time stable signal,where the concept short-time is referred to windowed time dimension.The whole time dimension is converted with the translation of parameter τ.That means,the transform makes use of the product of window function g(t−τ) and signal f(t)to implement windowing and translation.Then,Fourier transform is further applied.Formally,for any f(t)∈L2(ℝ),the transform is def i ned as

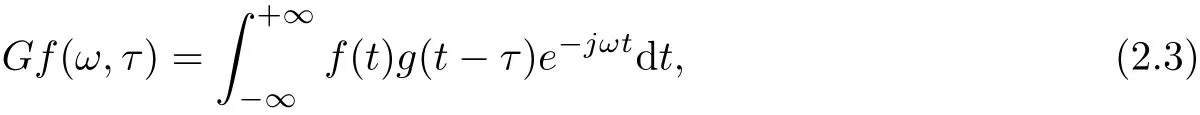
where g(t−τ)e−jωtis the integral kernel and|g(t)|2dt=1.The window function in Gabor transform is Gaussian function def i ned as

where parameter a is used to determine the width of the window function.

2.2Gabor Filter

As an important information carrier,texture gives frequency and direction information.The texture of a local area contains direction and frequency of narrow band,which can be extracted by using some appropriate f i lter.In this way,texture information is obtained as the output of the f i lter.Many of the f i lters can be used to extract texture feature,however,most of them can not produce ideal results in both time and frequency domains.

Gabor proposed one-dimensional elementary function family,which is also called Gabor function family[13].In order to apply it to the f i eld of biological visual neural receptive,Daugman extended such one-dimensional f i lter into two-dimensional Gabor f i lter[1415].In his solution,a f i lter bank composed of various f i lters with dif f erent parameters is proposed,which can signif i cantly extract rich characteristics of a local space,such as modulation characteristic, frequency selective characteristic,direction selectable characteristic.So it can produce desired result while simulating biological visual neural receptive.Daugman pointed that,although the primary functions of Gabor f i lter can not constitute a complete orthogonal set,but it can be regarded as a kind of wavelet f i lter to solve practical problems in image processing.Therefore, it is clear to understand that two-dimensional Gabor f i lter is extremely suitable for the texture which is rich in direction and resolution.

In the space domain,a two-dimensional Gabor function is a complex modulated sinusoidal grating using a two-dimensional Gaussian function,which is def i ned as

Correspondingly,the two-dimensional Gabor function is

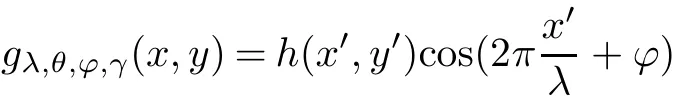
where x′=xcos θ+y sin θ,y′=−xsin θ+y cos θ,γ=σx/σy,σx=σ.

In Eq(2.6),parameter γ is called aspect ratio,ranges for 0.23＜γ＜0.92[16];coefficient λ is the wavelength of cosine function,which determines the frequency;the ratio σ/λ controls the frequency bandwidth of the f i lter of the basis function g(x,y).In fact,De Valois et al[17]have proved that

It shows that

Further in Eq(2.6),parameter θ(θ∈[0,π))gives the rotating direction of the coordinates, which also determines the direction of the f i lter.Parameterb is the bandwidth,and parameter ϕ(ϕ∈(−π,π])is the bias of cosine function.When ϕ=0 and ϕ=π,the function is centrosymmetric;when ϕ=π/2 and ϕ=−π/2,the function is antisymmetric around the center.As shown in Figure 1 we can get dif f erent shape of Gabor f i lter by setting dif f erent parameters of ϕ=0,ϕ=π/2,ϕ=π,ϕ=−π/2.Therefore,Gabor f i lter bank,which is composed of dif f erent f i lters with dif f erent parameters,provides f l exible tools to handle dif f erent practical problems.

Figure 1Gabor Filters in Dif f erent Parameter ϕ

2.3Gabor Feature Extraction

To extract the Gabor feature of an image,the f i rst step is to apply Gabor f i ltering to the image.This process is actually to perform convolution between the image and Gabor f i lter. Given an image f(x,y),after applying Gabor f i lter to the given image f(x,y),we get the f i ltered image as,

As shown in Figure 2,we take Barbara with size 512×512 as an example.The f i rst subf i gure is a presents the original image,and the else four subf i gures are f i ltered results respectively at direction 0,π/4,π/2 and 3π/4.

Figure 2Filtered Barbara under Dif f erent Directions

With the f i ltered image,texture features which describe every pixel and its surrounding neighborhood are extracted as the mean and standard deviation.According to the parameter setted in[10],four scales and six directions are taken into account in the Gabor f i lter bank. Therefore,features can be represented as vectors with totally 6×4×2=48 dimensions,and values in each dimension are normalized between 0 and 1.In order to fully make use of the advantages of the results from the Gabor f i lter bank,texture features are computed with W dif f erent evaluation window sizes.In this paper,we set W=5,which is corresponding to windows 3×3,5×5,9×9,17×17 and 33×33.As is known to all,the large window could ref l ect the regional consistency better,but go against the localization pixels in the edge of image;and inversly small window is more suitable to precisely def i ne the boundaries,but would inf l uence consistency inside regions of homogeneous texture.So our objective is to ensure regional uniformity,and can accurately position the edge pixels of image simultaneously.The detail description about the specif i c algorithm will be showed in Section 4.

§3.Prototype Selection

Traditional image segmentation algorithms,which are based on pixel classif i cation techniques,often make use of all pixels of training images.Given the fact that a pixel is represented as a 48-dimensional vector after feature extraction,the volume of data to be processed is huge. While this is a requirement for a test image,in which every individual pixel has to be classif i ed, it is not necessary or desirable for modeling the texture patterns of interest as the classif i cation cost highly depends on the number of prototypes.Thus,it is necessary to reduce this number, which is a suitable task for a clustering algorithm.

In[10]n-cut clustering algorithm was used for the prototype selection.But we know that n-cut clustering algorithm causes a high degree of computational complexity and it also shows that based only on local information,the normalized cut functional is not a suitable measure for the quality of clustering.Further,even with a suitable similarity measure,the f i rst few eigenvectors of such adjacency matrices cannot successfully cluster data sets that contain structures at dif f erent scales of size and density[18].In this paper,we choose weighted kernel k-means clustering algorithm[11]for the prototype selection because of its ef f ectiveness and lower time complexity.

§4.Texture Image Classif i cation Algorithm Based on Gabor Wavelet

After extracting feature and selecting the prototype,then there is the classi fi cation phase. The strategy for classifying a test image using multiple evaluation window sizes should apply large windows inside regions of homogeneous texture in order to avoid noisy classi fi ed pixels, and small windows near the boundaries between those regions in order to precisely de fi ne them. Previous work[10]has proposed a thought of as a top-down approach,which is a great idea to realize the strategy.

In this paper,we propose a new method for marking the pixels as unknown.As is discussed above,texture features are computed with di ff erent evaluation window sizes.De fi ne the evaluation window as W.The main idea of this paper is that,if the edges of the image are not contained in W,apply larger windows for the classi fi cation;and if the edges are contained in W,narrow the window until there is no edges in it.This idea could be realized by searching the character of initial classi fi cation result,that is if the pixel and its neighborhood belongs to the same class,we consider there is no edge in this window and label the pixel;if not,we don’t label it.Here the region unlabeled is considered as containing the edge of the image,and apply smaller window on it for further classi fi cation.

Let S be a feature set,s be the feature of the center pixel in the current window,{bs}is the classi fi cation result,where s∈S,bs∈N,N is the number of class.as∈A,A={1,0}is the label set.Set up as=1 which represents that there is no edge under the current window, otherwise as=0.(

where Q represents the 8 neighbors of each pixel,bsis the classif i ed result.Def i ne B= Bs(bs,as)|s∈S,bs∈N,as∈A,where Bsis a random variable based on S.When Eq(3.2) established,the feature satisf i es the Markov nature.That means the characteristic of the pixel under the current window only depends on its neighbors.

J Melendez et al[10]has not focused on the technique of marking the unknown pixels,in which only the edge pixels after post-processing and corresponding neighbors were simply labeled.We could summarize its thought as follow.

In every level,the classif i ed result has been post-processed f i rstly,def i ne the post-processed result as b′.And then detect its boundary pixels.The method of marking the unknown pixels is that,for every boundary pixelwhere Q′is the W×W neighborhood of boundary pixel.This method only marked the neighbors of the boundaries,which obviously couldn’t contain as much wrong-classif i ed pixels as our marking technique did.We also could tell from Figure 3.The f i rst subf i gure is a threetexture image,and through the classif i cation in the f i rst level we get the second subf i gure.The third subf i gure is the marking results using method in[16]and the fourth subf i gure is obtained via our marking technique.We could see that marking technique proposed in this paper ensure more wrong-labeled pixel being marked for the classif i cation in next level,which is conductive to obtain more accurate classif i cation results.

Figure 3Contrast of the Marking Methods

Afterwards pixel classi fi cation is performed by SVM classi fi er.In every level,after necessary pixels being marked as unknown,we only need to classify the unknown pixels.SVM has strong regularization properties.Regularization refers to the generalization of the model to new data. As is known that KNN classi fi er needs all available datas for the similarity calculation.This may lead to considerable overhead,if the training data set is large.So in view of the excellent classi fi cation performance of SVM,we choose this competent tool instead of KNN classi fi er. And experiment also has proved the correctness of the chosen.

Based on the above discussion,the algorithm of pixel-based texture classi fi cation through multi-level Gabor characteristic transfer is as follow.

Step 1Design the Gabor fi lter bank with 4 scales and 6 directions.

Step 2Pursue the Gabor fi ltering to the training image and test image,and obtain 24 fi ltered images.

Step 3Characterize every pixel of training image and test image by computing the mean and standard deviation of neighborhood of 33×33.

Step 4Use the weighted kernel k-means clustering algorithm to select the prototypes of every training image.

Step 5According to the training sets,classify all of the pixels of the test image by using SVM classi fi er.The initial classi fi ed image is obtained.

Step 6Search initial classi fi cation results to fi nd out whether every pixel and its 8 neighbor pixels are belonging to the same class,if it is not,label the pixel and its 33×33 neighbor pixels as unknown,that is as=0.

Step 7Characterize every pixel by computing the mean and standard deviation of the neighborhood of 17×17.Classify the test image pixels labeled as unknown.

Step 8Repeat Step 4 to Step 7 until the smallest available window is utilized.

Step 9Post-process the f i nal classif i ed image.

§5.Experimentation and Analysis

The proposed technique has been evaluated on composite images of well-known Brodatz[19]. Figure 4 shows the test image and its associated training images used in this paper,where the fi rst sub fi gure is the test image,the else two sub fi gures are the associated training images.

Figure 4Test Image and Its Associated Training Images

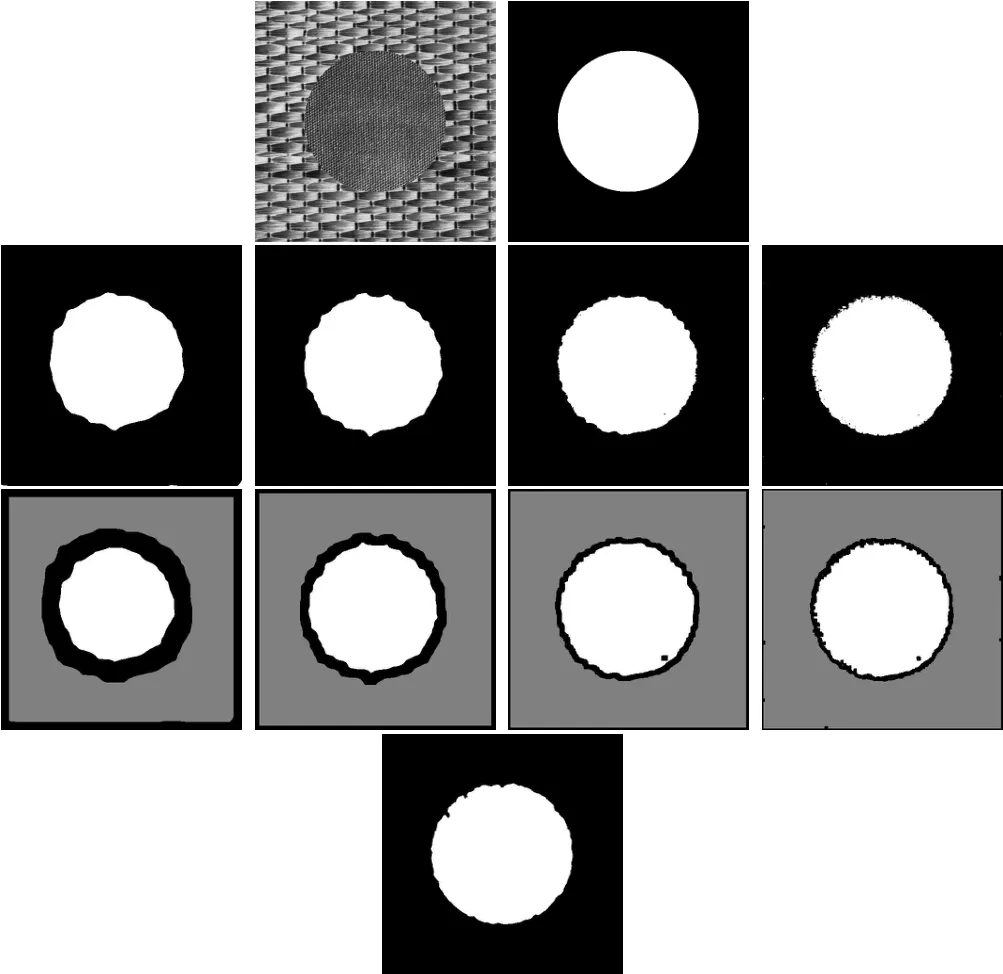
Figure 5The Classif i cation Process of Two-Texture Image and Corresponding Results

Figure 5 shows the realization process of the algorithm,taking two-texture image as anexample.The f i rst subf i gure is the original image and the second subf i gure is the corresponding perfect classif i cation.the third subf i gure is the initial classif i ed result.Execute step 6 to obtain the seventh subf i gure.The rest can be done in the same manner.The last subf i gure is the f i nal classif i ed result.

They prove that our algorithm has considered more wrong-labeled pixels and the classif i cation of boundary pixels gradually accurate trend is obvious.

§6.Conclusions

This paper presents a texture classi fi er based on Gabor wavelet that achieves good classifi cation rates.Accuracy near boundaries between regions of di ff erent textures is improved by utihzing multiple evaluation window sizes,according to a top-down approach that also contributes to speeding up the classi fi cation process,since only a reduced number of image pixels are classi fi ed by all available window sizes.The innovation is concentrated on how to mark the boundary pixels as unknown in each level during the transfer process.The proposed technique has ensured more wrong-classi fi ed pixels being labeled as unknown for the next step,which has yielded better results in terms of average classi fi cation rate.There naturally remain many interesting questions to be investigated.For instance,we could adapt the proposed methodology to unsupervised pixel-based texture segmentation.The goal in this case is to automatically determine sets of prototypes that characterize the di ff erent regions of homogeneous texture within a given image.

[References]

[1]HARALICK R M,SHANMUGAM K,DISTEIN I.Textural features for image classi fi cation[J].IEEE Trans Syst Man Cybern,1973,6:610-622.

[2]LIU L,FIGUTH P.Texture classi fi cation from random features[J].IEEE Trans Pattern Anal Mach Intell, 2012,34(3):574-586.

[3]RANDEN T,HUSOY J H.Filtering for texture classi fi cation:a comparative study[J].IEEE Trans Pattern Anal Mach Intell,1999,21(4):291-310.

[4]MELENDEZ J,PUIG D,GARCIA M A.Comparative evaluation of classical methods,optimized gabor fi lters and LBP for texture feature selection and classi fi cation[C].Austria:Springer Berlin Heidelberg,2007, 912-920.

[5]TSIAPARAS N,GOLEMATI S,ANDREADIS I.Comparison of multiresolution features for texture classiif cation of carotid atherosclerosis from B-mode ultrasound[J].IEEE Trans Infor Tech,2011,15(1):130-137.

[6]LATEGAHN H,GROSS S,STEHLE T.Texture classi fi cation by Modeling Joint distributions of local patterns with gaussian mixtures[J].IEEE Trans Image Process,2010,19(6):31-39.

[7]KHELLAH F M.Texture classi fi cation using dominant neighborhood structure[J].IEEE Trans Image Process,2011,20(11):3270-3279.

[8]OJALA T,PIETIKAINEN M.Multiresolution gray-scale and rotation invariant texture classi fi cation with local binary patterns[J].IEEE Trans Pattern Anal Mach Intell,2002,24(7):971-987.

[9]MANJUNATH B S,MA W Y.Texture features for browsing and image retrieval of image data[J].IEEE Trans Pattern Anal Mach Intell,1996,18(8):837–842.

[10]MELENDEZ J,PUIG D,GARCIA M A.Multi-level pixel-based texture classi fi cation through efficient prototype selection via normalized cut[J].Pattern Recognit,2010,43(12):4113-4123.

[11]DHILLON I S,GUAN Y Q,KULIS B.Kernel kmeans,Spectral Clustering and Normalized Cuts[C].New York:ACM,2004,551-556.

[12]CORTES C,VAPNIK V.Support vector networks[J].Mach Learn,1995,20:273-297.

[13]GABOR.Theory of communication[J].J IEEE,1946,93:429-457.

[14]DAUGMAN J.Complete discrete 2-D Gabor transforms by neutral of image analysis and compression[J]. IEEE Trans Acoust Speech,1988,36(7):1169-1179.

[15]DAUGMAN J.Uncertainty relation for resolution in space,spatial frequency and orientation optimized by two-dimensional visual cortical fi lters[J].J Opt Soc Am A,1985,2(7):1160-1169.

[16]JOENS J P,PALMAR A.An evaluation of the two-dimensional Gabor fi lter model of simple receptive fi elds in cat striate cortex[J].J Neurophysiol,1995,58(30):1233-1258.

[17]DEVALOIS R L,ALBRECHT D G,THORELL L G.Spatial frequency selectivity of cells in macaque visual cortex[J].Vision Res,1982,22(5):545-559.

[18]NADLER B,GALUN M.Fundamental limitations of spectral clustering[J].In Advanced in Neural Info Process Syst,2007,19:1017-1024.

[19]BRODATZ P.Textures:a Photographic Album for Artists and Designers[M].New York:Dover Publications, 1966.

tion:94A08

CLC number:O174.22Document code:A

1002–0462(2014)02–0307–10

date:2013-10-30

Supported by the National Natural Science Foundation of China(61071189);Supported by the Key Project of Science and Technology of the Education Department of Henan Province(14A120009); Supported by the Program of Young Scholar of the Peoples Republic of Henan Province China(2013GGJS-027)

Biography:DENG Wei-bing(1978-),male,native of Pingdingshan,Henan,a lecturer of Henan University, engages in applied mathematics.