基于Delaunay三角剖分的PCB检孔机多重孔位校正方法
2014-07-31蔡宇王静
蔡 宇 王 静
(广东正业科技股份有限公司,广东 东莞 523808)
1 前言
1.1 背景介绍
PCB检孔机就是一种高度智能化的PCB钻孔自动检测设备[1],用来对PCB制作过程中钻孔检测,快速地检测出孔的数量,并且对出现孔大、孔小、孔多、孔少、孔内异物以及孔的重心偏移这几种错误类型进行判定。
在PCB光电检孔机检测过程中,标准档与测试档对应孔位的配准作为关键步骤,显得尤为重要,其配准效果直接影响判定结果。由于目前PCB板整体制作工艺的提升,孔径越来越小、孔间距越来越近[2]。对PCB检孔机测试过程的孔位配准技术也提出了更高的要求, 因此本文提出了一次粗配准加两次细配准的多重孔位校正技术,可以快速可靠地实现测试档数据与标准档数据的的匹配,大大降低孔位配准错误的概率。
1.2 相关概念
1.2.1 三角剖分[3]
假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
(1)除了端点,平面图中的边不包含点集中的任何点;
(2)没有相交边;
(3)平面图中所有的面都是三角面,且所有三角面的合集是散点集V的凸包。
1.2.2 Delaunay三角剖分
在定义Delaunay三角剖分之前,需要给出Delaunay边的定义:假设E中的一条边e(其端点为a、b),若e满足条件:存在一个圆经过a、b两点,圆内不含点集中任何其他的点,这一特性又称空圆特性,则称之为Delaunay边[4]。
利用Delaunay边,Delaunay三角剖分定义为:如果点集的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。它具有如下特征:
(1)空圆特性;
(2)最大化最小角特性。
2 由粗到细的孔位校正算法思想
为了实现标准档与测试档的孔径信息比对,必须在空间坐标上实现配准,故快速而准确地实现大规模散乱点云数据的配准是PCB检孔机孔径检测的关键环节。
理论上,测试档数据与标准档数据是一一对应的,但是实际中由于同一块PCB板不同位置加工的精度不同[5](如PCB的边缘以及不需要插入电子元件的孔的位置,其加工精度比需要插入电子元件的钻孔精度要差)、扫描过程中平台振动导致的横向误差、以及运动过程中速度不一致和不同位置摩擦系数不一致导致的纵向误差、板子翘曲导致的局部形变等,都会造成实际得到的测试档孔位会偏离标准位置, 并且这种偏差是无法避免的。考虑到目前PCB板整体制作工艺的提升,孔径越来越小、孔间距越来越近。对PCB检孔机测试过程的孔位配准技术也提出了更高的要求,因此本文提出了一次粗配准和两次细配准的多重孔位校正技术,可以快速可靠地实现测试档数据与标准档数据的的一一匹配。
多重孔位校正方法分为三个步骤。 如图1所示,第一步是利用PCB板四个角点处的定位孔圆心信息对标准档和测试档孔位进行仿射配准,得到初始的空间对应关系,该步骤称之为粗校正。第二步将测试档中“较大”孔径的孔提取出来作为Delaunay三角剖分点集[6],并计算其与标准档对应孔之间的位移偏差。 第三步计算测试档中“较小”孔径的孔落在了三角剖分中的位置,然后利用其对应的三角形三个顶点信息对其进行校正。 上述两个步骤称之为细校正。
3 算法流程
为了描述方便,文中引入如下标记,假设表示标准档所有孔中心坐标集合,表示测试档中所有孔中心坐标集合,A、B、C、D为标准档的四个定位孔圆心,A’、B’、C’、D’为测试档的四个定位孔圆心,D1表示最小孔径,D2表示最小孔边距,E表示系统整体的最大误差。
3.1 全局粗校正
考虑到PCB定位孔一般位于四个角处、孔径较大、特征明显且比较容易和普通钻孔区分开来,以下内容假定定位孔信息是已知的。
如图2所示,根据标准档S和测试档T的定位孔之间的对应关系,可以利用最小二乘拟合出其仿射变换矩阵M1。 令T1=M1T, 那么T1便是通过定位孔信息校正后的测试档中心集合。
3.2 全局细校正
在实际应用中发现,如果最小孔间距D1,最小孔径D2和系统最大误差E满足如下条件:
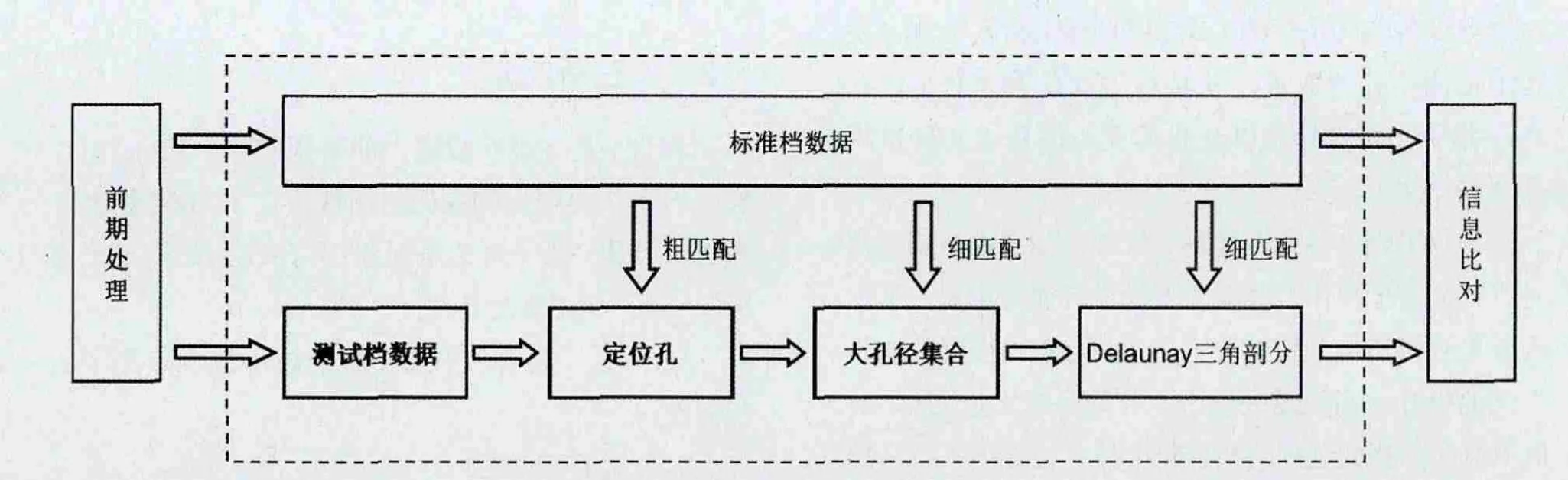
图1 PCB信息配准定位流程图
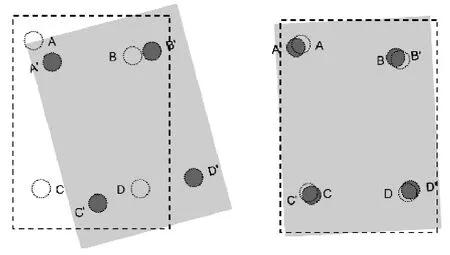
图2 标准档与测试档之间对应的定位孔
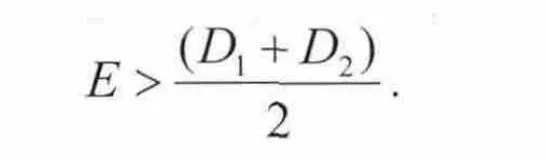
那么就会出现误匹配。考虑到目前PCB制造向小孔径、高密度的方向发展,在系统误差无法避免的情况下,误匹配现象发生的概率会越来越大。反之,如果D2足够大,比如D2>2×E,那么理论上,对于任意孔间距,都不会发现误匹配现象。
文中的数据的全局细校正方法基于上述事实,首先从标准档S中提取子集S_large,并满足如下条件:
对于任意s∈S_large,其孔径大于2×E。
S_large 中元素分布比较均匀。
S_large 中元素个数适中。
由于S_large中的元素满足条件(1),故S_large中的元素可以直接计算出其在T1中的对应点。 已知对应点后,可以计算出S_large=(s1,s2.......)和T1_large=(t1,t2.....)之间的偏移量集合, 记为Offset=(o1,o2......)满足下式:

又由于S_large是从标准档S中提取的,且由于PCB板钻孔工艺可能出现的瑕疵,S_large中的每个元素在测试档T中不一定都存在对应元素。这时候标准档与测试档的子集对应的Delaunay三角剖分不一致。避免该问题最简单的方法是对S_large进行初始筛选, 将在T不存在对应元素的点剔除掉,这样就保证了Delaunay三角剖分的一致性。
下面以筛选后的S_large作为Delaunay三角剖分集合,对其集合中元素进行Delaunay三角剖分,如图3所示:(a)为初始的S_large集合,(b)其Delaunay三角剖分图DT。以该三角剖分作为基准,下面进行细校正步骤2。

图3
3.3 局部细校正
假定集合S_small=S_large, 即S_small是S_large对应的补集,由S_large的定义可知,S_small中的元素s一般是孔径比较小的,且落在Delaunay三角剖分图DT的某一三角片内。 这样,可以利用DT中三角片三个顶点的信息来校正s。

图4 s落在DT中某一三角片内、外两种情形
对于任意∈S_small,其校正步骤如下:
(1)计算s落在DT内三角片的三个顶点坐标。
(2)假定落在△ABC内,其中A、B、C∈S_large。那么:
计算s与A、B、C之间的距离,记为lA、lB、lC。
由3.2节,已经计算出S_large中元素的空间偏移量,故A、B、C三点的偏移量OA、OB、OC可以作为已知量。
计算s的加权偏移:
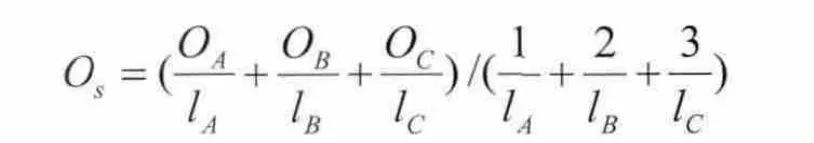
(3)如果s落在DT中所有三角片外部,如图4所示,那么只需要考虑距离其最近的两个点。偏移量计算方式和(2)相同。
以上校正环节可以概述为以下三点:
(1)利用定位孔信息对原始孔中心集合进行全局的仿射变换;
(2)对于大孔径的孔,一般不会出现误匹配现象,故可直接利用仿射矩阵对其进行校正处理;
(3)对于小孔径的孔,利用大孔径集合构成的Delaunay三角剖分进行局部校正。
4 试验与结果分析
4.1 不同大小的S_large划分方式试验结果
考虑到Delaunay三角剖分算法的时间复杂度较高,检孔机的实时性要求也很高。所以S_large的选取非常重要,既要考虑到后期校正的精度,也要顾虑到时间开销。文中选择孔数46754的PCB钻孔板,设置不同大小的S_large,其Delaunay三角剖分及校正时间开销如表1所示。
从表1中可见,S_large的数目控制在5000以内时,基本上可以满足实时性要求。实际操作中,可以只在第一次检测时进行Delaunay三角剖分计算,之后的检测可以直接利用其剖分作为初始剖分网格。需要注意的是,初始剖分网格和实际检测中的网格不一定完全一致,还需要对网格点进行筛减,幸运的是,Delaunay三角网格的局部调整是很容易处理的。采用这种方式处理的话,表1中的Delaunay剖分耗时可以忽略不计。经验证,文中校正算法增加的时间可以控制在100 ms以内。
4.2 校正结果与不校正结果比较
为了测试文中提出的方法,选择三种不同孔数,不同孔径的PCB做对比试验。 其中板A孔数为33523,板B孔数为148381,板C孔数为6427。对比试验结果如图5所示。其中(a)、(c)、(e)是未校正时所有孔的位移偏差绝对值,(b)、(d)、(f)是校正之后的所有孔的位移偏差绝对值。从图对比结果可以看出,利用文中的校正技术处理之后,孔位偏差明显优于未校正的情况。
5 结论
基于Delaunay三角剖分的PCB检孔机多重孔位校正技术,可以快速准确地实现多孔数、高密度、小孔间距的PCB板的孔位配准,保证了图像的配准精度。实验结果表明:文中提出的算法能够完全满足检测要求的精度和实时检测的快速性要求。

表1 Delaunay三角剖分及校正时间开销
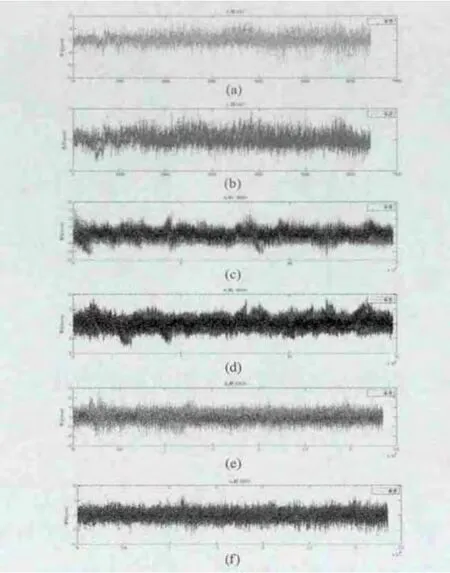
图5 测试结果对比图
目前,上述算法和理论研究均成功地应用于ASIDA品牌的PCB光电检孔机JK-3200,达到PCB 孔径检测的技术指标,目前已经推向了市场,用户反应良好。
项目来源:2012年广东省数控一代机械产品创新应用示范工程专项资金入库项目专题“关键技术攻关与行业数控装备类”重大项目《名称:面向数控一代的印刷电路板及其精密联装关键设备研发与产业化》;立项批文:粤科高字(2012)150号。
[1]陈志云.印制电路板检测系统的研究与应用[D].重庆:重庆大学, 2006.
[2]姚晓栋,张永宏,吴琦等. 基于图像识别的印制电路板精密检测实验研究[J]. 测控技术, 2006,25(6):75-77.
[3]申利民. Delaunay三角剖分算法优化的实现[J]. 计算机与数字工程, 2009:34-36.
[4]李小丽,陈花竹等. 基于格网划分的Delaunay三角剖分算法研究[J]. 计算机与数字工程, 2011:57-59.
[5]秦超华. 印制电路板设计与工艺的技术探讨[J]. 西安航空技术高等专科学校学报, 2004,2(5):35-38.
[6]余杰,吕品等. Delaunay三角网构建方法比较研[J].中国图像图形学报, 2010:1158 -1165.
