“挤压-挠曲”复合底鼓机理及相似模拟技术研究
2014-07-30崔健
崔 健
(太原理工大学 矿业工程学院,山西 太原 030024)
国内外专家学者对巷道底鼓机理及控制技术做过大量的研究,并取得了一定的成果,但是对于深部巷道底鼓问题研究较少,特别是受两侧掘进影响的巷道。一方面煤矿深部巷道底板岩层呈层状分布且有明显的软岩特性,巷道开挖后,围岩应力平衡结构被破坏,产生二次或多次应力重新分布,造成底板浅部岩层固有裂隙贯通形成破碎岩体;另一方面随着相邻巷道的掘进影响,对底板深部完整层状岩层二次挤压,形成了底鼓峰值位置不在底板中央的“挤压-挠曲”复合底鼓的特殊现象,加之深部巷道受地下水影响明显,使得底鼓机理更加复杂。正是由于现有理论不能全面细致地分析这类深部巷道复合底鼓机理,从而难以有效地控制底鼓量,不能保证巷道的正常使用,所以,继续对这类非对称条件深部巷道层状底板“挤压-挠曲”复合底鼓稳定性研究很有必要。
1 工程概况
阳煤五矿皮带运输巷位于+211水平(地面标高+1 040 m),巷道两侧为南轨道运输巷和北轨道运输巷,其空间布置位置见图1。由于底板呈层状分布,表层为强度较低的泥岩,深部为砂岩,巷道开挖后,围岩应力重分布,底板表层岩层强度较低,受到支承压力的影响最先折曲、破坏。随着北轨道巷和南轨道巷的先后掘进,挤压浅部由开挖造成的破碎岩体以及深部还处于完整层状的岩体,产生了挤压流动性和挠曲褶皱性的复合底鼓,同时底鼓峰值位置靠近一帮。

图1 皮带运输巷的空间位置图
2 非对称条件下“挤压-挠曲”复合底鼓机理分析
2.1 巷道两帮传递机理
确定巷道围岩结构时,以关键层理论及上覆岩层砌体梁理论为基础确定上边界[1-3]。当巷道开挖后,围岩应力重新分布,两帮在支承压力的作用下发生变形甚至破坏形成极限平衡区。由于两帮的支承压力近似对称,在巷道断面中心建立直角坐标系,分析巷道右断面,见图2。

图2 一帮受力计算模型图
由于两帮松软,泊松比也相对较大,而帮部与顶板、底板的交界面处内聚力c0和内摩擦角φ0比帮部岩体低,此时极限平衡区岩体趋向于从顶板、底板挤出。假设:极限平衡区与弹性区交界处满足:
σy│x=x0=kγH,σx|x=x0=λkγH
(1)
式中:
k—应力集中系数;
γH—原岩应力;
λ—极限平衡区边界侧压力系数。
纵向选取巷道单位长度的岩体作为研究对象,进而可以得到极限平衡区ABCD水平方向的合力:
P=mAkγH-mPi
(2)
式中:
m—帮部高度;
mPi—帮上由支架提供的水平支护力。
由于支承压力和水平合力P的共同作用,使得极限平衡区内岩体经历了弹性应变、塑性应变、蠕变应变。这里忽略蠕变应变,得到岩体变形位移S1为
S1=Se+Ss+Sd
(3)
式中:
Se—岩体的弹性位移;
Ss—岩体剪胀后与顶板、底板间的剪切位移;
Sd—岩体扩容引起的变形量。
2.2 底板最大破坏深度
底板破坏深度的计算,一般可采用土力学中地基计算方法,由塑性理论可知在底板上极限平衡区分为3个区,见图3。
随着支承压力的持续增加,当超过底板主动区(Ⅰ区)极限强度时,极限平衡区宽度内的底板将在底脚处与岩体分离。主动区的岩体受到上方垂直压力的作用而发生变形破坏,形成破碎区。同时,由于水平作用力的影响将岩体进一步挤压到过渡区(Ⅱ区),并把应力传递于这一区域。过渡区继续挤压被动区(Ⅲ区),使得岩体在主动区支承压力的影响下向巷道内移动,并形成剪切滑移面,形成不同程度的底鼓。

图3 底板中的极限平衡区图
2.3 “挤压-挠曲”复合底鼓模型
阳煤五矿皮带运输巷开挖后浅部底板受支承压力影响,发生折曲、破碎;深部底板尚未发生破坏,岩层呈层状分布。随后经历了南北轨道巷的掘进影响,其中北轨道巷先掘进,在二次水平应力的作用下,浅部破碎岩体受挤压发生挤压流动性底鼓,深部完整层状岩体发生挠曲褶皱性底鼓;随后的南轨道巷掘进也会促使这类复合底鼓的产生,只是第二次影响更为激烈,其帮部应力包括了此次掘进产生的支承压力及上次掘进后残余的支承压力,其力学环境见图4。巷道底鼓模型见图5,其中x01与x02分别为两帮的极限平衡区长度。

k1—北轨道巷掘进支承压力形成的高支承压力区应力集中系数 γ—上覆岩层平均容重,N/m3 k2—南轨道巷掘进支承压力和残余支承压力叠加形成的高支承压力集中系数

图5 巷道底鼓模型
3 深埋巷道底鼓相似材料模拟实验
3.1 模型相似常数和基本参数
根据原型尺寸和模型实验条件,确定了几何相似比为CL=1∶20,容重比为Cr=1∶1.25,则其应力比为Cσ=CL·Cγ=1∶25。因此,σv、σh、σc、σt及E的相似常数也均为25。实际围岩区域为20 m×20 m×4 m,巷道断面为5 m×3.5 m,模型中断面大小为25 cm×17.5 cm。模型模拟了埋深800 m的巷道,巷道的原岩垂直应力为20 MPa,水平应力为10 MPa,而模型中的垂直应力和水平应力分别为0.8 MPa、0.4 MPa,对应的相似材料见表1。
实验加载方案:1)用预先设定好的木条制成矩形巷道形状,按照设计的相似配比配制材料,装入模拟架,并将压力加到预定值,放置1周左右,使得模型固化完全后,打开巷道窗口。2)当加载应力小于巷道围岩的原岩应力时(σ<0.8 MPa),采用水平应力和垂直应力同时加载的方式。3)当加载应力大于原岩应力且小于3倍原岩应力时(0.8 MPa<σ<2.5 MPa),水平应力按照垂直应力的0.5倍加载,过程采用先加垂直应力再加水平应力且水平应力持续增大。4)当加载应力大于3倍原岩应力时(σ>2.5 MPa),水平应力与垂直应力同时加载。

表1 模拟材料配比表
3.2 相似材料模拟结果分析
采用高清晰度单反照相机固定在同一位置进行拍摄,然后用CAD处理照片,计算围岩测点的变形量,通过DH3815静态应力监测系统监测应力变化。底板上测点布置图见图6,共布置了3排测点,第1排测点与底板下边界相距0.5 m(这里均表示为实际尺寸),每排测点横向竖向间距均为1 m,其中1-2、2-3、3-2布置在巷道的中心位置。巷道加载后底板的破坏情况见图7,由图7可以看出靠近巷道底板的两角处产生了与水平呈35°左右的剪切错位,由于岩层被自由面和破坏面切割,加之水平力的作用,底板岩层发生破坏形成菱形块体,巷道底板发生明显底鼓,这是岩层水平位移和竖直位移的合成结果[4]。

图6 巷道底板测点布置情况

图7 巷道加载后底板破坏情况
巷道底板垂直应力为图8。

图8 巷道底板垂直应力图
分析图8可以得出,巷道开挖后测点的垂直应力迅速上升,3-2号测点先上升至13.7 MPa左右,然后随着时间的推移逐渐减少直到底板破坏;同一水平线上的3-1号测点,其垂直应力最大值高于3-2号测点的最大值,这说明巷道底板中部的垂直应力最小,同时在水平上越远离巷道底板岩层中部其垂直应力越大;对比竖向3-2、2-3、1-2三个测点后,同样可以得到竖向方向远离底板位置的垂直应力更大;整体应力波动值不大,但2-1号显示出了逐步上升的趋势,直到底板明显破坏,陡升至20 MPa左右,这是底脚处应力集中造成的。
巷道底板水平应力为图9。
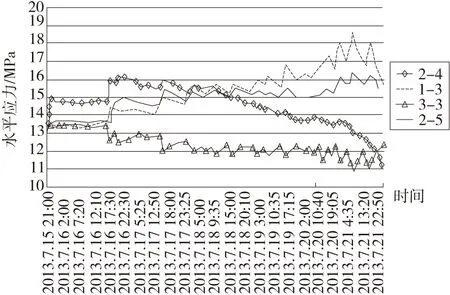
图9 巷道底板水平应力图
由图9可以看出,对于3-3测点的水平应力呈现出先迅速上升至原岩应力而后逐步下降,说明底板以下0.5 m左右岩体为破坏区;分析2-4和2-5测点,巷道开挖后应力值有所增加并稳定了一段时间,随后发生一次明显的应力升高,在同一时期的1-3测点却发生突降,这是因为底板破坏,水平应力转移到深部造成深部应力值增大。比较图8,9可以看出,底板以下同一水平的岩层,中部属水平应力降低区,而两边一定范围的岩体属水平应力升高区。巷道底板拉移分布规律见图10。

图10 巷道底板位移分布规律图
由图10可见,随着深度的增加,垂直位移逐渐减小,最大底鼓量为605 mm,发生在巷道底板中心位置,这是由于巷道受到对称力作用没有水平位移;底板向下超过3 m范围基本没有竖向位移,而水平方向在1/2的巷道宽度范围内。
综上现象分析说明,对于深埋巷道,随着巷道开挖,底板垂直应力和水平应力都会快速上升,但上升幅度不同,并且维持时间短,这是由于深埋高应力的作用使得底鼓很快产生,使得应力值降低。对底板位移分布规律的分析可以得出,深埋巷道底鼓量较大且多发生在底板中心位置,这符合一般的底鼓发生规律,但是若巷道两侧受到不同的支承压力时,会在底板水平方向产生位移,与垂直位移合成会产生偏向一帮的底鼓。
4 结 论
1)建立一帮受力的计算模型,分析了极限平衡区内支承压力的分布状态,在考虑帮部弹性位移、剪切位移的同时引入了扩容位移,最后推导出帮部位移的表达式,由表达式可以看出两帮的位移与顶底的相对移近量有直接关系,可见控制帮部的位移对底鼓的防治有一定的作用。
2)建立“挤压-挠曲”复合底鼓巷道模型,认为此类复合底鼓发生的条件是底板呈层状分布且较为软弱。巷道开挖后浅部发生折曲破碎深部还保持完整,随后经历了两侧相邻巷道先后掘进的影响,挤压浅部破碎岩体及深部完整岩体,由于两帮支承压力的不对称造成了偏向于一帮的“挤压-挠曲”复合底鼓现象。
3)分析浅部挤压流动性底鼓时,以最大破坏深度为研究范围,将底板破碎岩体看作等效岩性参数连续介质来处理,假设了位移为零的位置结合变分原理对此类底鼓进行了分析;对深部挠曲褶皱性底鼓采用了薄板弯曲理论估算底鼓量。最终推导出非对称条件下“挤压-挠曲”复合底鼓峰值位置及确定底鼓量大小和形态的表达式,对底鼓量的估算及确定底鼓发生位置有一定的指导意义。
4)以相似材料模拟试验为基础,分析了深埋巷道底板变形、垂直应力和水平应力分布的一般规律,可知深埋巷道开挖后,越远离底板中央,应力值越大,同时底板垂直应力和水平应力都会不同幅度的迅速增加,但持续时间短,这是由于深埋高应力的作用使得底鼓很快产生,应力值降低。至于深埋巷道底板的变形,其位置位于底板中心且垂直位移量很大。这对研究非对称条件下深埋巷道“挤压-挠曲”复合底板围岩变形规律有所裨益。
参 考 文 献
[1]杨双锁.回采巷道围岩控制原理及锚固结构的适应性研究[D].徐州:中国矿业大学博士学位论文,2001.
[2]杨双锁,康立勋,钱鸣高.煤矿回采巷道支护-围岩相互作用全过程分析[J].岩石力学与工程学报,2002 (21):1978-1981.
[3]于远祥,牟志杰,白永彪.挤压流动性隧道底臌机理及控制技术[J].中国公路学报,2012(05):105-112.
[4]王吉松.关英斌,鲍尚信,等.相似材料模拟在研究煤层底板采动破坏规律中的应用[J].世界地质,2006,25(1):86-90.
