复杂构造区二维地震勘探需要注意的问题
2014-07-30孙玉民郑艳清曾维望
孙玉民,郑艳清,曾维望
(1.阳泉市南煤集团有限责任公司, 山西 阳泉 045000;2.山西省煤炭工业厅 煤炭资源地质局,山西 太原 030012; 3.山西山地物探技术有限公司, 山西 晋中 030600)
二维地震勘探是煤炭煤层气勘探过程中的一个重要环节。二维方法主要以构造为首要任务,从理论上来说,其具有先天的方法局限性,从20世纪30年代以来,研究人员就这一问题展开了大量的讨论[1],已形成了明确的认识―在深部地层发生复杂或局部强烈构造变形的情况下,二维地震勘探方法的局限性表现的更为突出[2]。因而,在合理部署地震勘探方案的基础上,尽可能提高成果精度,并合理利用其成果,指导实施地质钻探工作,在当前煤炭资源勘探向深部以及复杂区发展的趋势下,是一个不可忽略的问题。
本文从典型案例出发,分析了在复杂断块区二维地震勘探部署不当的情况下,地震资料难以归位的根本问题,易导致构造控制程度不足和工作量浪费等工程问题。讨论了在二维地震数据空间分布不规则且方向性强,数据少且横纵向分布不均的不利条件下,利用二维时间剖面数据和时深转换速度进行计算机地质成图时可能出现的错误,并提出了相应的对策。
1 复杂构造条件下的偏移归位问题
根据反射波勘探理论,当地层水平及近水平时,二维地震不存在归位问题。如果地震测线与地层走向大角度相交且地层埋深较浅时,二维偏移处理的归位效果较好,成果剖面上构造与形态的空间偏移误差相对较小,一般也可以忽略。
但是,地层的构造形态一般较为复杂,在勘探前是未知的或有一个大致的轮廓,存在一个明显的逐步认识的过程。无论是预(概)查、普查、详查还是精查勘探阶段,二维地震主测线在绝大多数情况下都不可能是真正的倾向测线,或与断层等线性构造的走向正交,而联络测线则往往与地层、构造走向线平行或小角度斜交。在这种情况下,无论是叠加还是偏移数据,反映的地层形态都不是沿测线各点铅垂线方向上地层的赋存形态,而是通过测线的射线平面与地层分界交线上的空间形态,而且偏移量的大小取决于目的层深度、地层倾角、上覆地层速度等因素[3]。地层的埋深越大、赋存形态变化越剧烈(倾角大和倾向变化大),地层速度越高,偏差越大,可达数十、数百米甚至更多。事实上,此时地震剖面上各点所对应的实际反射点位往往与地表测线位置存在较大的偏差(见图1)。避免偏差或归位不准的有效方法是合理布设地震测量,尽可能避免测线与地层和断裂等线性构造的小角度相交。

图1 地震测线位置及目标层反射点空间位置示意图
2 地震部署不当的典型案例
在大断裂发育的情况下,如断块区,地层产状变化剧烈,而且断面波、断点绕射、侧面波、回转波等与构造有关的异常波发育。如果勘探测网布置不合理,如网度过大或者测线与构造和地层的走向夹角过小,二维偏移处理无法归位,很难去除上述异常波,而且目标层反射点线与测线之间离散度更大,很容易造成钻井失败或地震工作量浪费的问题。
某探区位于沁水盆地南部,测线网度为5 km×10 km。失利探井M1井布置在地震测线上(见图2),过M1井测线(NEE走向)的二维地震偏移剖面解释成果(见图3),剖面上波组关系清晰、特征明显,预测980 m见3#煤层。但实际钻井揭露一正断层, 620 m见3#煤层,明显变薄,缺失的二叠系下盒子、上石盒子和部分石千峰组地层厚约300 m,没有达到指导探井施工的目的。
通过垂直与原测线的补充二维勘探发现,该探井失败的主要原因是M1参数井恰好处在F3、F4两正断层夹持的断块边缘(图2),断层两侧地层发生了明显的局部牵引现象,倾角变陡。测线的网度过大,与构造复杂程度不匹配,工作量不足导致控制程度变差。其次是测线方向布设不合理,原地震测线方向与过孔断层走向基本平行(夹角10°),通过三维模型与地震波的模拟发现,原二维地震时间剖面在井位附近实际反映的完全是断层下降盘煤层面法线方向上的形态,见图4(右)阴影区,南距M1孔约260 m,而不是原测线正下方的地层形态,因而在原地震剖面井位附近没有断层的迹象,二维偏移没有任何作用。补充过井剖面及地震射线示意图见图4(右)。

图2 QN探区二维地震勘探部署图

图3 过M1井NEE向地震剖面解释图
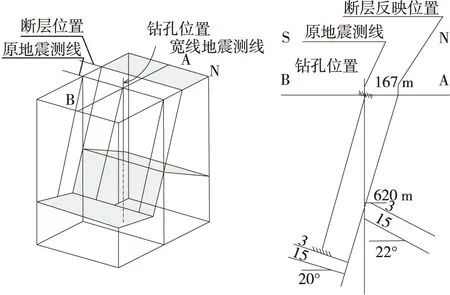
图4 M1井区推测三维地质模型图(左)补充过井剖面及地震射线示意图(右)
与之相反的情况是断块区测网布设过密造成的工作量浪费问题,见图5。该区测网密度为0.5 km×1 km,图5上部剖面对应的测线上,目的层反射波成像质量高,断点清晰,容易对比解释,可靠性强。而与其正交的测线(图5下),两端与断裂小角度相交,中部处于断块内,由于其与断层走向交角较小,且过于靠近断面,波场变得极为复杂,无法对比解释,可利用程度低,工作量基本浪费。
以上案例说明,在深部复杂区进行二维地震勘探部署时,应注意:
1)充分收集探区内基础地质和物探成果,在构造分区的基础上,根据构造复杂程度合理规划测网密度。构造复杂程度中等或以上时,测网不宜过大,以免出现控制程度不足的问题。
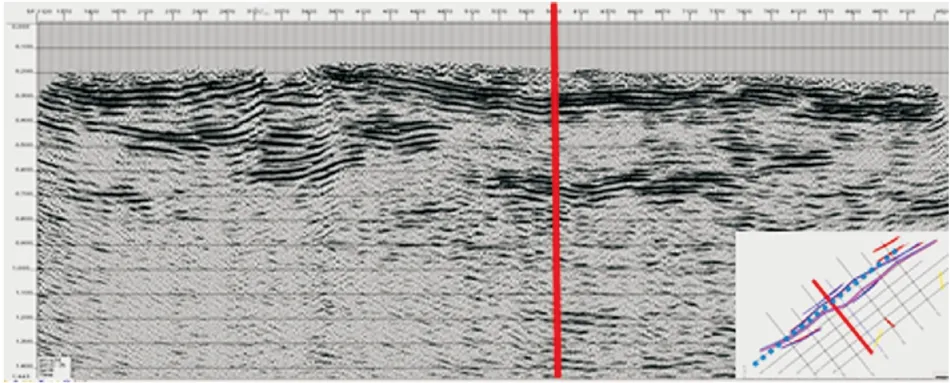
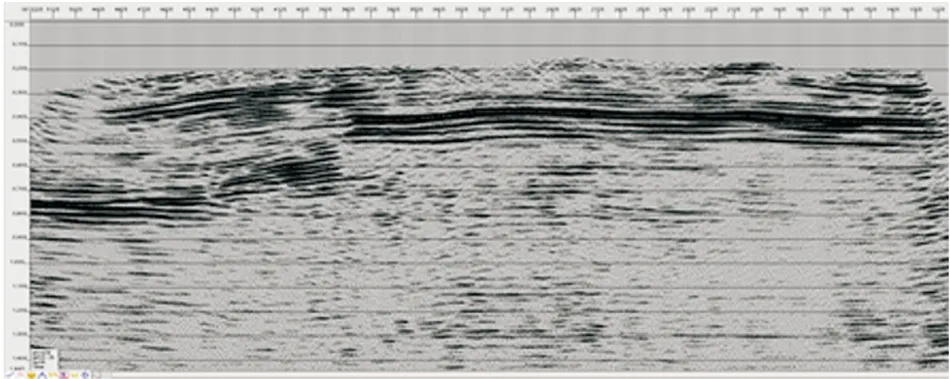
图5 断块内两正交测线地震时间剖面图
2)在大规模断裂构造区布设联络方向测线时,测网不宜过密,如果过于靠近断面,地震工作量容易被浪费。
3)地层赋存形态复杂时,必须考虑二维地震归位不准的问题,进行空间归位校正。根据校正结果,优选探井位置,部署到地震测线以外。为进一步规避勘探风险和减小深度误差,可在井位处补充布设二维宽线或一条正交二维测线。
3 复杂构造条件下的地质成图问题
复杂构造条件下的地质成图精度主要依赖地层及断层的空间归位或校正精度,空间校正可利用水平叠加剖面,也可以利用叠偏剖面。一般来说,偏移剖面较水平叠加剖面有许多优点,如绕射波大部分收敛,反射波沿测线基本或部分归位,干涉带被分解,断层及其特征也较明显。用偏移剖面编制构造图,空校方法比水平剖面简单, 空校后不会出现断层两盘“打架”、“裂开太宽”等不合理现象。地层变形较小时可直接换算成深度图;变形较大时,在构造扭曲或转折部位、断点处,再作一次垂直于测线的校正,即可完成三维空间的校正[4-7]。
深部构造复杂区往往需要在叠偏剖面的基础上,作正交方向上的二次偏移归位,因此,偏移量的大小仍取决于目的层深度(时深转换速度和T0值)、地层的倾角和倾向[8]。当前地质成图方法多采用计算机自动成图技术,利用T0值和时深转换速度,通过空间插值、网格化间接获得空间曲面的深度、各节点的倾角和倾向,继而完成空间校正。
离散数据网格化方法众多, 常用的网格化方法可分为四大类趋势面拟合、插值、综合法、克里金法,但是都有其局限性,克里金法相对来说效果较好[9]。当数据点分布均匀、规则时,大多数情况下可以得到理想的网格化数据(见图6)。但是,在二维地震数据空间分布极不均匀的不利条件下,无论哪种计算机自动网格化方法,二维测线间的空白数据区的速度和T0值的最终网格化数据的质量、精度和可信程度会明显降低[10],需要人工干预,使计算机绘制的速度和T0值平面更符合地质和地球物理规律。

图6 不同数据分布特征图(引自Daniel J.Tearpork[10])
数据空白区的有效人工干预可以参考标准地质图、野外地质填图(基岩出露区)和槽探、坑探(第四系覆盖区)等地质数据,通过空白区内优选关键点,测量地层产状数据来检验和约束时间、速度和深度平面图,提高二维地震数据的归位准确性,进一步减小最终二维勘探成果图的误差。
另外,勘探井穿透的煤层往往是多层的,当沉积环境稳定且煤层间距较大时,地震资料中也会有与其对应的反射波信息,会涉及多层成果图的绘制任务。实际工作中通常会碰到有上部煤层而没有下部煤层数据的情况,见图8,编号a井仅钻遇A层,b井则穿透A、B层。也就是说,做为关键约束条件,不同井中不同煤层的控制程度是不同的,上部煤层往往更高一些。由于在不存在角度不整合面的情况下,相邻层之间实际垂直厚度不如地层表面复杂[10],因此,可以考虑采用层间时差和层间速度获得层间厚度,再用约束条件更多的上部煤层深度减去层间距,估算下部煤层的构造形态,其精度可能要高于单纯利用下部煤层反射波的T0值和该层的平均速度直接计算得到的构造图。
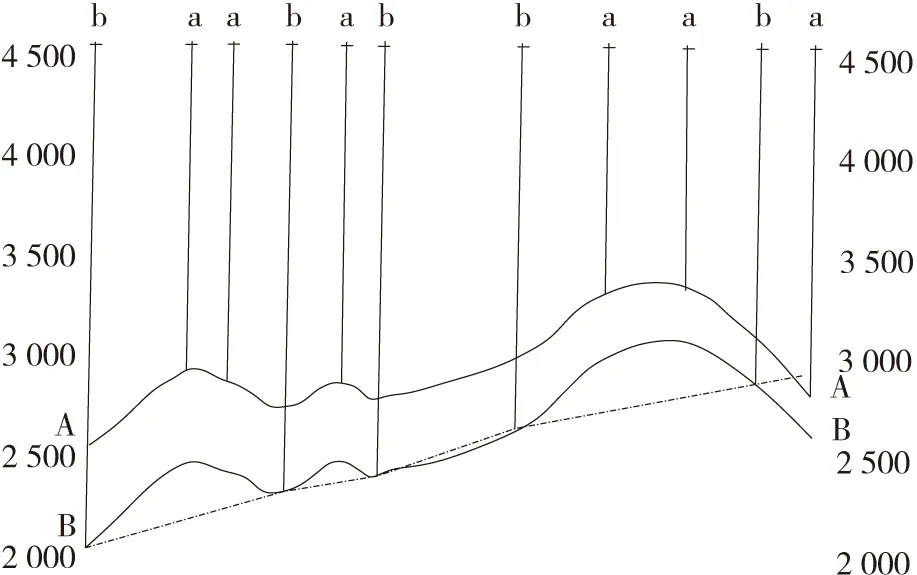
图8 多层情况下的井约束差异(引自Daniel J.Tearpork[10])
4 结 语
充分认识二维地震资料的归位不准问题,特别是深部复杂构造变形区,地震测线与反射点位的偏差更不可忽视,这种情况下,实现二维数据的完全归位是不可能的,只能减小其误差。此外,复杂构造变形区的计算机成图方法也需要加强研究[11],而三维地震是查明深部复杂构造和地层形态的根本方法。
参 考 文 献
[1]L.R.Denham,杨静芬.为什么大的发现并非如此之大:二维勘探的局限性[C].美国勘探地球物理学家学会第61届年会论文集,1991:140-144.
[2]邹传皎.地震二维归位问题和三维地震勘探[J].石油物探,1988,27(4):79-88.
[3]陆基孟.地震勘探原理(下)[M].北京:石油工业出版社,1990:33-35.
[4]刘素庚.用叠偏剖面直接编制构造图[J].石油地球物理勘探,1984,19(5):560-572.
[5]丁艳红,夏东岭,李志勇,等.对二维地震剖面的解释与成图方法的认识[J].石油物探,2002,41(2):211-215.
[6]顾先觉,吴剑锋,祁红林,等.二维地震偏移剖面对比解释作图新方法[J].石油物探,2005,44(1):80-83.
[7]李丽贤.二维地震剖面闭合差校正及构造成图方法研究[J].石油天然气学报,2010,32(2):232-235.
[8]祝伟业,张 权.二维叠偏剖面作图中值得注意的问题[J].石油物探,2000,39(3):100-107.
[9]程红杰,胡祥云,田米玛,等.地震数据网格化方法研究[J].工程地球物理学报,2006,3(1):28-32.
[10]DanielJ.Tearpork,RichardE.Bischke,蔡希源,等.实用构造法地下地质制图[M].北京:中国石化出版社,2008:17-23.
[11]黄本宇,王家华,王湘波.复杂地质构造的等值线填充及实现[J].阜阳师范学院学报(自然科学版),2006,23(4):50-52.
