一类新的2+1维非线性发展方程及其解的对合表示

刘亚峰， 刘 炜

(石家庄铁道大学数理系，河北石家庄 050043)

0 引言

无穷维发展方程的可积性是当今数学物理研究的一个重要方面。将无穷维系统转化为有限维完全可积系统是证明可积性的基本思想之一［1］。Lax对非线性化方法是获得有限维可积系统的有效工具。近年来非线性化方法被用于求解高维孤子方程［2］，如2+1维Toda方程、2+1维K-P方程等。现研究一个新的2+1维非线性发展方程。首先通过两个二阶谱问题之间的相容性条件获得非线性发展方程，得到其Lax对。利用Bargmann约束将谱问题转化为一个Bargmann系统，并将Lax对非线性化，获得一个有限维Hamilton正则系统，并证明此系统在Liouville意义下是完全可积的。

1 二阶谱问题及非线性发展方程的Lax对

讨论二阶谱问题

式中，∂=∂χ且 ∂－1∂=1;u=u(x，t);ν=ν(x，t)∈R 为该谱问题的位势函数;λ 为特征值;φ 为对应于 λ 的特征函数。

在基础空间Ω=(-∞，+∞)上讨论特征值问题(1)，假设u，ν，φ为无穷远速降的函数。

命题 1［3］:

(1)如下二阶谱问题。

构成完整谱系。

(2)若φ，ψ是谱系(2)的特征值λ所对应的特征函数，则

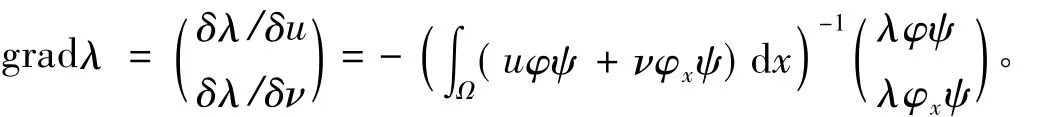
设辅谱问题为φt=Wφ，其中

令 gj=( －bj，aj)T，j=0，1，2，…，则由相容性条件 φxxt=φtxx得如下递推关系

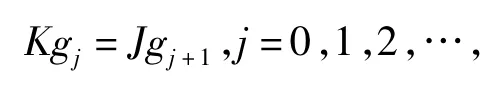
其中

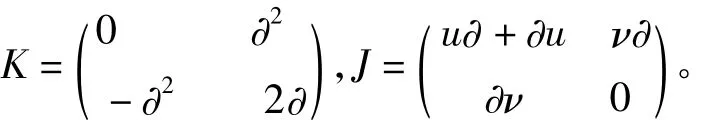
直接计算可知

定理1:在等谱条件(λt=0)下，非线性发展方程族为

对应的Lax对为

特别，当m=0时，发展方程为

当m=1时，发展方程为

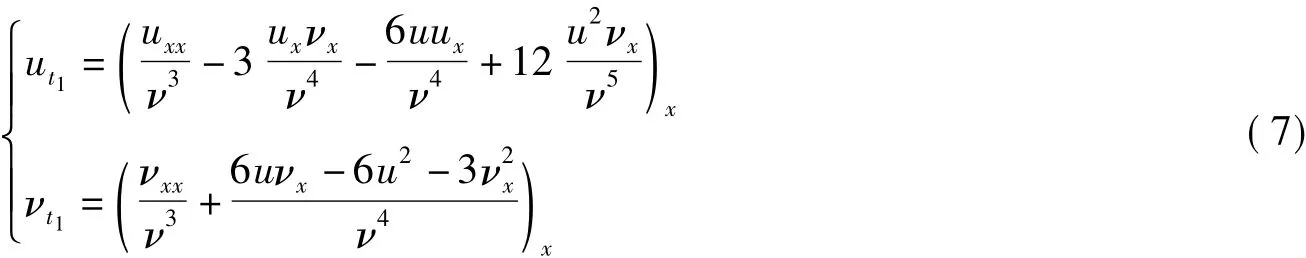
令t0=y，t1=t，则得到一个新的2+1维发展方程

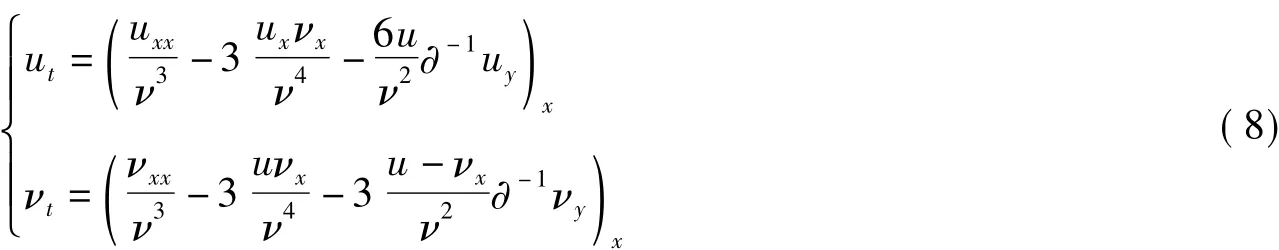
2 Bargmann约束与Hamilton正则系统

设谱系(2)的 N 个不同的特征值为 λ1＜ λ2＜ … ＜ λN，φj，ψj为对应于 λj(j=1，2，…，N)的特征函数［4］，令 Λ =diag(λ1，λ2，…，λN)，φ =(φ1，φ2，…，φN)T，ψ =(ψ1，ψ2，…，ψN)T。

命题2:设 Gj=( ＜ Λj+1φ，ψ ＞ ，＜ Λj+1φx，ψ ＞)，则 KGj=JGj+1。

证明:由式(4)直接计算可得。

令g0=G0，得到Bargmann约束

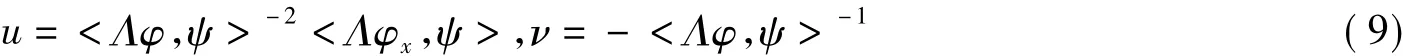
由此，谱系(2)等价于如下Bargmann系统

现在寻求与Bargmann系统(10)对应的Hamilton系统的J-O坐标。

定义 Lagrange 函数:^I= ∫ΩIdx，其中，I= ＜ φx，ψx＞ － ＜ Λφ，ψ ＞－1＜ Λφx，ψ ＞ 。

命题3:Bargmann系统(10)等价于如下Euler-Lagrange方程:

设q1，q2为广义坐标，p1，p2为广义动量，Hamiltom函数则 q1，q2，p1，p2满足如下方程［5］

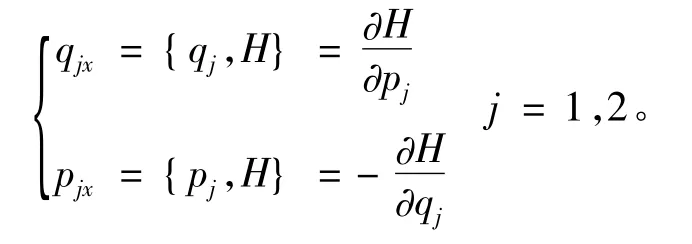
构造Jacobi-Ostrogradsky坐标如下

在坐标系(11)下，Bargmann约束化为

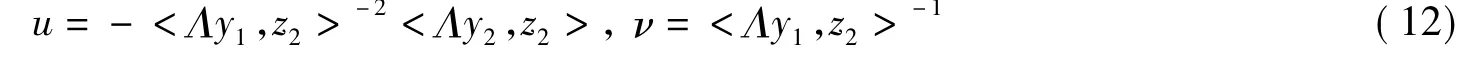
Bargmann系统(10)等价于如下Hamilton系统

此时

3 Hamilton系统的完全可积性

定理2:在Jacobi-Ostrogradsky坐标(11)下，发展方程族(4)所对应的Lax对(5)等价于如下形式［3，6，7］

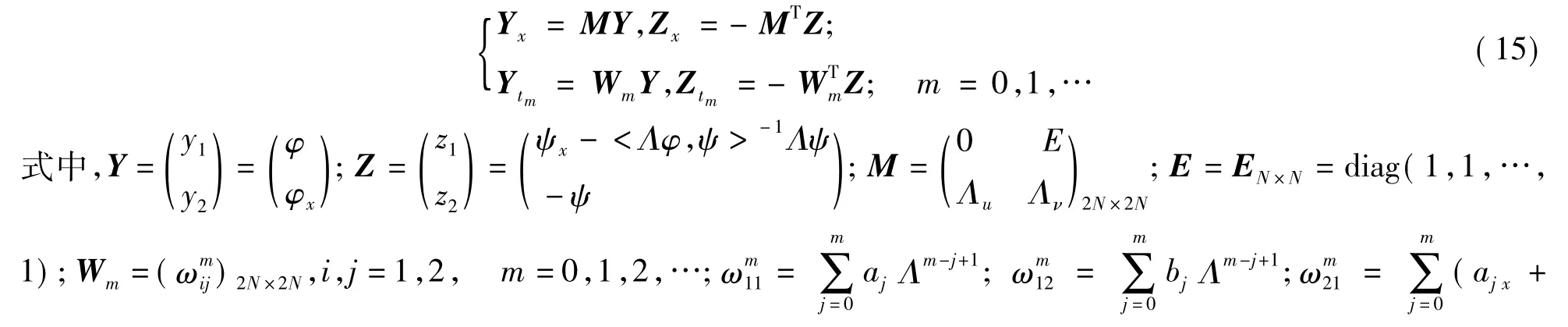
定理3:在Bargmann约束(12)下，发展方程族(4)的Lax对(5)被非线性化为如下Hamiltom方程

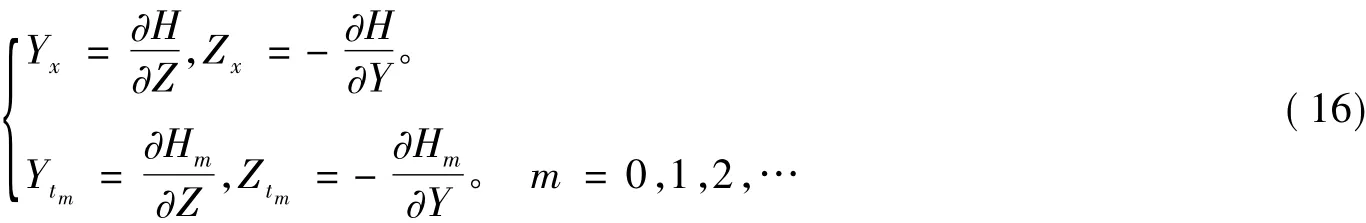
下面讨论Hamiltom系统的完全可积性［7］。

令

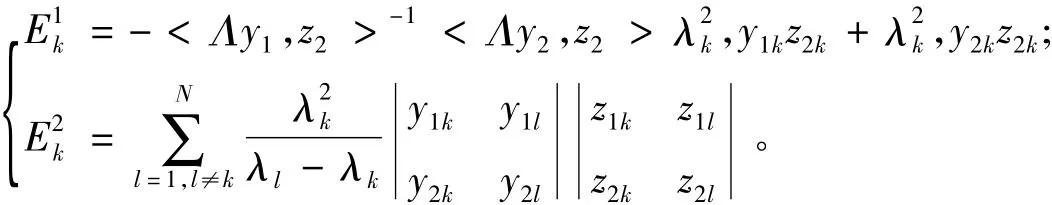
定理4:

(1)

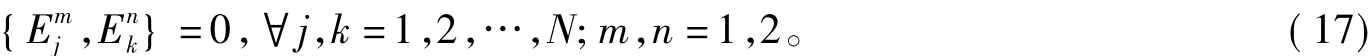
定理5:Hamiltom系统(16)在Liouville意义下是完全可积系，并且Hamiltom相流可换。

证明:由(17)式直接计算得 {Πμ，Πλ}=0，{Hm，Hn}=0，m，n=0，1，2，…。

所以{H，Hm}=0， m=0，1，2，…

由Arnold定理，Hamiltom系统(16)是完全可积系，且Hamiltom相流可换。

定理 6:设(y1，y2，z1，z2)满足 Hamiltom 系统(16)，则式(12)

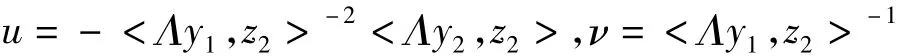
为非线性发展方程族(4)的对合解。

特别，如果(u(x，y，t)，v(x，y，t))是方程(6)和(7)的相容解，则(u(x，y，t)，v(x，y，t))为2+1 维非

线性发展方程(8)的解。

［1］谷超豪，曹策问，李翊神，等.孤立子理论与应用［M］.浙江:浙江科学技术出版社，1990.

［2］Cao Cewen，Wu Yongtang，Geng Xianguo.Relation between the Kadometsev-Petviashvili equation and the confocal involutive system［J］.J.Math.Phys，1999，40(8):3948-3970.

［3］Gu Zhuquan.The Neumann system for the 3rd-order eigenvalue problems related to the Boussinesq equation［J］.IL NUOVO CIMENTO，2002，117(6):675-632.

［4］Cao Cewen，Geng Xianguo.Classical integrable systems generated through nonlinearizaton of eigenvalue problems［M］.Berlin:Springer-Verlag，1990.

［5］Arnold V I.Mathematical Methods of Classical Mechanics［M］.Berlin:Springer，1978.

［6］Gu Zhuquan，Zhang Junxian，Liu Wei.Two new completely integrable systems related to the KdV equation hierarchy［J］.IL NUOVO CIMENTO，2008，123(5):606-622.

［7］Zhao Ye，Gu Zhuquan，Liu Yafeng.The Neumann system for the 4th-order eigenvalue problem and constraint flows of the coupied KdV-type equations［J］.Eur.Phys.J.Plus，2012，127:77.