关于不定积分∫sec xdx的另解
2014-07-25葛亚平
葛亚平
(南通理工学院 基础课教学部,江苏 南通 226002)
关于不定积分∫secxdx的另解
葛亚平
(南通理工学院 基础课教学部,江苏 南通 226002)
文献[1]对∫secxdx的求解作了较详细的解答,在文献[1]的基础上从第一类换元积分的角度对∫secxdx给出了另外两种求解方法.希望可以进一步帮助学生更好地掌握第一类换元积分的本质,从而丰富课堂教学内容,提高学生的数学素质.
不定积分;第一类换元积分;正割函数
一元函数微积分主要包括一元函数微分和一元函数积分两部分内容,而一元函数积分又分为不定积分和定积分两大类,由牛顿—莱布尼兹公式可知,只要会求解不定积分,定积分也就迎刃而解了.由此不定积分的求解在整个积分教学中是尤为重要的.
求解不定积分的方法较多,一般有第一类换元积分法、第二类换元积分法及分部积分法,对于高职学生而言掌握起来是有一定难度的.文献[1]中对于∫secxdx[2]的求解从第一类换元积分法的角度给出了5种不同的解法.本文在文献[1]的基础上,仍然从第一类换元积分的角度对∫secxdx再给出两种不同的解法,希望进一步帮助初学者更好地掌握求解不定积分方法的本质.
1 “1”的转化
三角函数不定积分的求解比较灵活,其中将1转化为sin2x+cos2x是一个常用的且行之有效的方法.

所以

2 转化为有理分式
三角函数的不定积分,通常可以使用万能公式
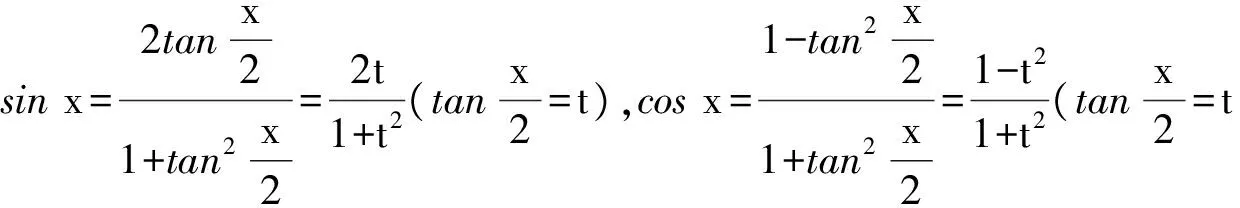
通过万能公式将原来的三角函数转化为有理分式函数,从而简化求解过程.


以上两种求法均是从第一类换元积分的角度从发,找到合适的整体,凑出其微分从而求解.如何找到合适的整体是关键,这就需要学生有良好的数学基础和细心的观察力以及对题目的理解力.当然不定积分的求解也不能拘于某一种方法,而是要将3种方法合理运用.要做到这一点就需要学生多多练习,举一反三,真正理解方法的本质.
[1] 赵继红. 关于不定积分∫secxdx的几种求解方法[J]. 湖南文理学院学报:自然科学版,2012(3):5-7.
[2] 同济大学数学系. 高等数学:上册[M]. 6版.北京:高等教育出版社,2007:199.
Another Methods for Indefinite Integration ∫secxdx
GE Ya-ping
(DepartmentofBasicCourse,NantongPolytechnicCollege,Nantong226002,China)
Based on reference [1], anther two methods for the indefinite integration ∫secxdxfrom the first kind of element integral are given. It can help students understand the first element integral nature better, and improve student’s mathematics quality further.
indefinite integration; the first kind of element integral method; secant function
2014-03-27
南通理工学院教研课题《高职学生数学素质培养的研究》(教研201304)
葛亚平(1981—),女,江苏南通人,南通理工学院基础课教学部讲师.
10.3969/j.issn.1007-0834.2014.04.018
O175.8
A
1007-0834(2014)04-0072-02
