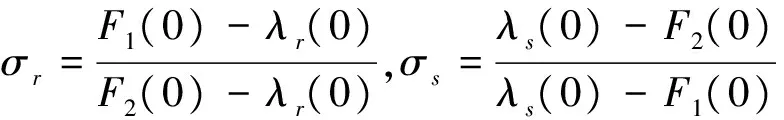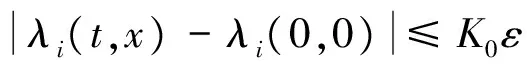对角占优矩阵在偏微分方程中的应用

刘志红

(郑州财经学院 计算机系，河南 郑州 450044)

对角占优矩阵在偏微分方程中的应用

刘志红

(郑州财经学院 计算机系，河南 郑州 450044)

主要讨论对角占优及严格对角占优(strictly diagonally dominant)矩阵的相关引理和定理，以及在偏微分方程边值问题中的应用(指数衰减因子).

对角占优矩阵；边值问题；衰减因子；特征根；整体经典解

对角占优矩阵是应用非常广泛的矩阵类，较多出现于经济价值模型和反网络系统的系数矩阵及某些确定微分方程的数值解法中[1-2].

定义1 n阶方阵A=(aij)n，如果其主对角线元素的绝对值大于同列(行)其他元素的绝对值之和，则称A=(aij)n是行(列)对角占优阵,即满足

(1)

定义2n阶方阵A=(aij)n，若存在β>1，使得

由定义1和定义2可知，若A是严格占优矩阵则一定是对角占优矩阵，若A是严格对角占优矩阵，则关于它的线性代数方程组有解.

由文献[3],有以下引理1.

(2)

由引理1可证明下面的定理1.

定理1 若A是行(列)对角占优矩阵,即A满足(1)式,则

证明 仅证行占优情形,对于列占优同理可证.情形1)的证明见文献[3].

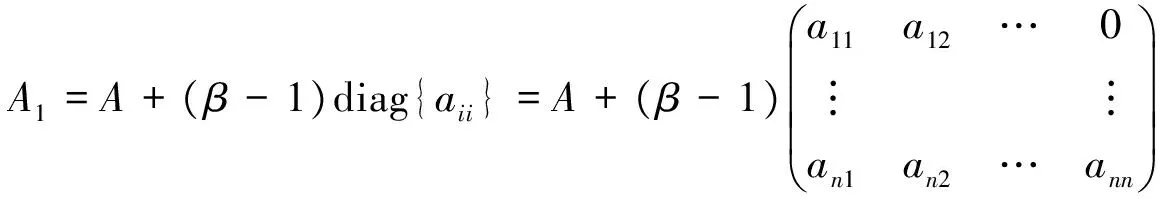
(3)

可见A1的主对角线上元素为βaii,i=1,2,…,n.再作A2=A+(β-1)aI，其中I为单位阵,可见A2的主对角线上的元素为(β-1)a+aii,i=1,2,…,n，在(1)式两边同时乘以β,得

(4)

由引理1及(3)式,可知A1是严格对角占优的.

(5)

因A2的主对角线上的元素为(β-1)a+aii,由(5)知A2也是严格对角占优的,即∃δ2>0,使得A2所有特征根μi,i=1,2,…,n，由引理1，有Reμi≥δ2.

而由

即有

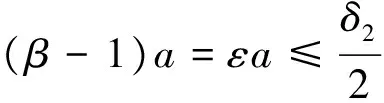
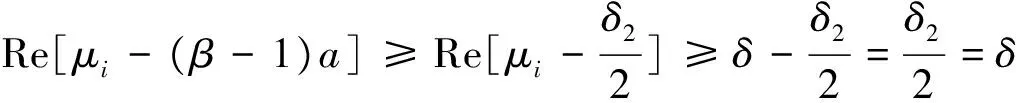
这时,即证得了在(1)式下，(2)式成立.至此,定理1证毕.

注记 (2)式中引入的“δ”即为双曲型微分方程中的指数衰减因子.

下面讨论指数衰减因子δ在具耗散项拟线性双曲型方程组的边值问题中的应用.一般来说,拟线性双曲型方程组的边值问题在t>0上并不存在整体经典解,这主要是因为边界数据的存在造成在边界上反射波的强度可能会大于入射波的强度,或者在边界上有波的连续反射现象发生[4]，但对于特殊的边界情况则不同.

考虑具耗散项拟线性双曲型方程组

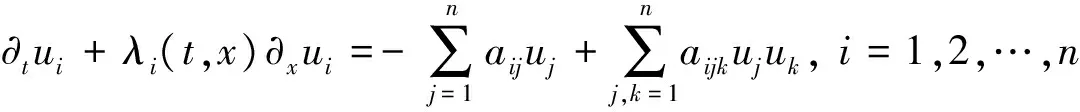
(6)

(7)

在光滑边界x=x2(t)(x2(0)=0)上，

(8)

其中x1(t)0，记xl(t)=Fl(t),l=1,2.

这里需要作适当的假设，

假设H1λi,θijk,θij,gijk,gi,Fl(t)是适当光滑的函数,且在t≥0上保持有界.

假设H2 边界条件(7)～(8)式存在唯一的解u≡u0(不失一般性，设u0=0).

假设H3 过原点的特征线不进入区域D,即λr(0)

令

则得到不等式

0≤σr,σs≤1 ,r=1,2,…,m;s=m+1,m+2,…,n.

假设H4A=L(0)▽g(0)L-1(0)=(aij)是对角占优的,即(1)式成立,由定理1可知(2)式成立.

定理2 在假设H1～H4之下，如果存在充分小的ε>0使

定理2的证明可通过一致先验估计，接着沿特征线积分，再根据局部延拓法可得.

[1] 刘法贵.具线性退化特征拟线性双曲型方程组的Cauchy问题[J].华北水利水电学院学报,1999,20(4):63-67.

[2]LIUFAGUI.Cauchyproblemforquasilinearhyperbolicsystems[M].Zhengzhou:YellowRiverConservancyPress,2006:33-38.

[3]LITATSIEN.Globalclassicalsolutionsforquasilinearhyperbolicsystems[M].NewYork:Wiley, 1994:1 263-1 317.

[4]GREENBERGJM，LITATSIEN.Theeffectofboundarydampingforthequasilinearwaveequation[J].JofDiffEquations, 1984(52): 66-75.

Application in the Partial Differential Equation ofDiagonally Dominant Matrix

LIU Zhi-hong

(DepartmentofComputer,ZhengzhouInstituteofFinanceandEconomics,Zhengzhou450044,China)

The diagonally dominant and strictly diagonally dominant (strictly diagonally dominant) related lemma and the theorem of matrix are discussed, and the application of boundary value problems of partial differential equations (exponential attenuation factor) is also stated.

diagonally dominant matrix; boundary value problem; attenuation factor; characteristic root; global classical solution

2014-05-14

刘志红(1983—)，男，河北邯郸人，郑州财经学院计算机系讲师.

10.3969/j.issn.1007-0834.2014.04.005

O175.27

A

1007-0834(2014)04-0020-03