缝洞储集层测井最优化处理

冯周，李宁，武宏亮，刘英明，夏守姬，原野

（1.中国石油勘探开发研究院；2.北京大学地球与空间科学学院）

0 引言

缝洞型碳酸盐岩、火山岩油气藏是目前中国油气勘探的重点领域，但这类储集层往往呈现出极强的非均质性与各向异性，通过测井识别地层岩性和流体性质存在较大困难。传统的POR（单孔隙度程序）、CRA（复杂岩性程序）等处理方法一般采用固定的解释模型分步计算地层参数，计算出的地层组分类型有限，难以满足缝洞储集层测井评价的需要。

20世纪80年代初，斯伦贝谢公司提出了测井资料最优化处理方法[1]。与传统处理方法不同，最优化处理是将所有的测井信息、误差及地区地质经验综合成多维信息复合体，通过数学中的最优化技术求取满足地层条件的最优解释结果，为复杂储集层测井评价提供了有效途径。随后，众多国内外学者对最优化处理方法进行了改进和完善，并取得了较好的地质应用效果[2-3]。

测井最优化处理的基础是依据地层模型建立各类测井响应方程，这些方程表征了测井响应与地层特性参数之间的定量关系，其精度决定了最优化处理结果与实际地层的符合程度。现有的最优化处理方法中测井响应方程都是基于均匀层状地层模型建立的[4]，在常规均质储集层中能取得较好的应用效果，但在非均质、各向异性缝洞储集层中，受岩性变化及孔隙分布影响，地层测井响应特别是电阻率响应变化更为复杂，计算得到的地层组分含量特别是孔隙流体组分含量存在较大偏差。因此，本文提出针对缝洞储集层的测井最优化处理新方法，并通过模拟计算和实际测井资料处理对方法可靠性进行验证。

1 测井响应方程

设目标缝洞地层由l种骨架矿物、n种黏土矿物、孔隙水及油气组成。仪器探测范围内，各骨架矿物的体积分数为Vmi，各黏土矿物的体积分数为Vcj（包含一定量的束缚水），孔隙水与油气的体积分数分别为Vw和Vhyd。

对于常规测井，其响应方程仍可根据体积模型统一表述为：

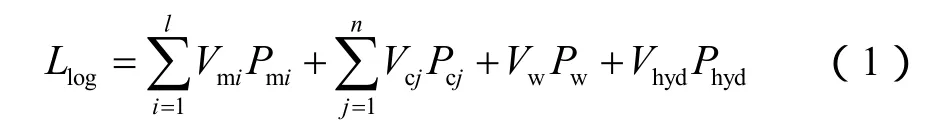
对于电阻率测井，其响应方程通常根据由各类饱和度模型描述的地层电阻率与含油气饱和度的关系来建立，传统的最优化处理方法中以Archie公式及其改进模型为主，不能反映复杂缝洞孔隙结构对地层电阻率的影响。李宁[5]于1989年以非均质各向异性地层模型为基础，通过完整的数学推导，给出了地层电阻增大率与含水饱和度之间的一般关系式：

在大量岩电实验测量和数据分析的基础上，李宁[5]给出了（2）式在缝洞储集层含水饱和度评价时的最佳截短形式：

（2）式表达了非均质复杂储集层电阻率与含水饱和度的精确定量关系，但在现有技术条件下，确定（2）式中的所有待定参数十分困难。（3）式用尽量少的待定参数和尽量简单的表达形式获得了尽可能高的计算精度，碳酸盐岩、火山岩全直径岩心实验及油田应用证实了该式的正确性[6-8]。

根据地层电阻率与地层因素、电阻增大率的一般关系式，电阻率测井响应方程可表示为：

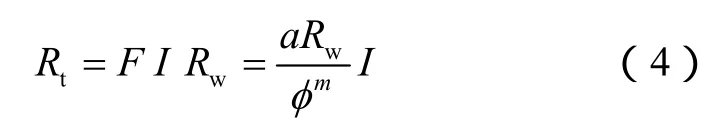
将（3）式代入（4）式，则非均质、各向异性缝洞储集层原状地层电阻率可表示为：

同理，冲洗带地层电阻率可表示为：

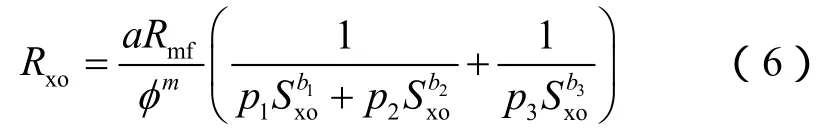
（5）式中地层总孔隙度φ、含水饱和度Sw可用地层流体组分含量来表示：

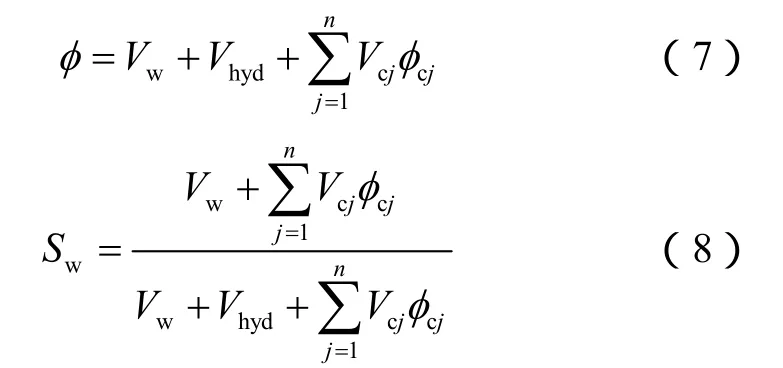
2 测井最优化问题求解

（5）式—（8）式为缝洞储集层电阻率测井及其他常规测井响应方程，其中各组分的响应参数可通过理论计算或实验方法确定[9-11]。对给定的地层解释模型，可由测井响应方程列出各测井曲线的理论测井响应值：

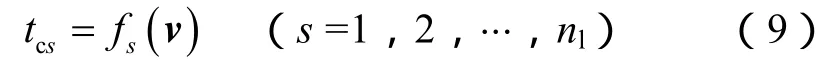
由最小二乘理论可建立测井最优化目标函数：

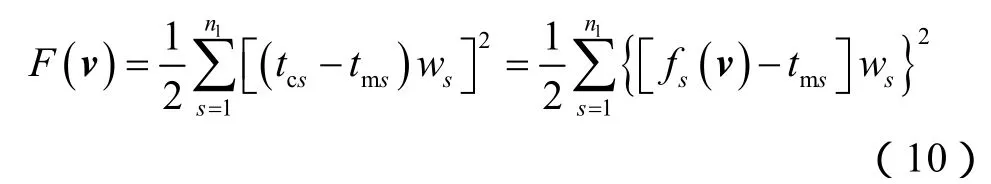
同时，地层组分还应满足一定的岩石物理及地质约束条件，约束条件方程组一般形式可记为：

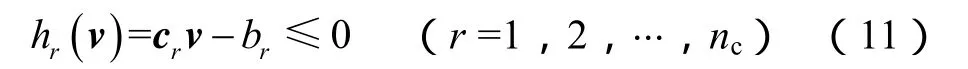
由（5）式、（6）式可见，理论电阻率响应是关于地层组分含量的复杂非线性函数，则求解最优化目标函数取最小值时的v的问题是一个典型的带约束条件的非线性最小二乘问题。以往的测井资料最优化处理方法研究中，研究者对测井最优化问题的求解算法进行了一些探讨与分析[12-15]，但主要针对线性最优化问题，对非线性最优化问题一般采用多目标最优化问题的通解算法，没有针对测井最优化目标函数最小二乘形式的特点求解，因而求解效率和计算精度有限。因此，本文结合惩罚函数法和 Levenberg-Marquardt算法[16]对目标函数进行求解。

首先，利用惩罚函数法，将约束问题转化为无约束问题，无约束问题目标函数为：

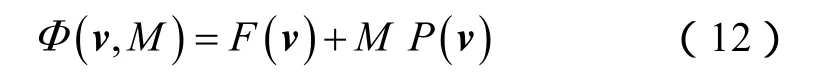
当v满足约束条件（hr(v)小于等于0）时，惩罚项M P(v)为零；当v不满足约束条件时，M P(v)大于0，且随M的增大而增大，当M趋于无穷大时，无约束问题的最优解v*将充分趋于约束区域的边界，此时v*也是满足约束条件的最优解。

针对约束问题目标函数的形式，惩罚函数可设为约束条件的平方和形式：

根据（10）式—（13）式，无约束问题目标函数可表示为：

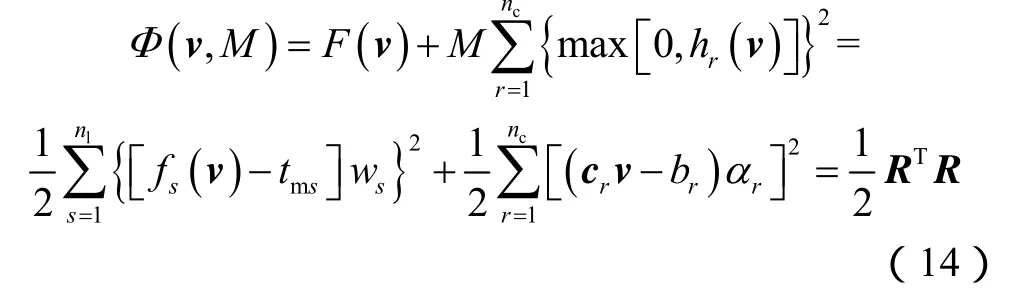
其中

对无约束非线性最小二乘问题，可利用Levenberg-Marquardt算法进行求解，其每步的迭代增量可通过如下的正则方程组来计算：

（15）式中，阻尼因子μ反映当前迭代点目标函数实际下降量与 1阶近似下降量的差异，在计算中自适应调整。求解（15）式，即可得到每步的迭代增量，当迭代解满足精度要求且满足（11）式时，即可认为求得最优解。

当阻尼因子较小时，（15）式即为Gauss-Newton法最优步长计算式；当阻尼因子很大时，（15）式则为蜕化梯度下降法的最优步长计算式。因此，本文提出的算法同时具有Gauss-Newton法的局部收敛性和梯度下降法的全局特性，具有较高的计算效率和精度。此外，该算法在计算过程中只需要求解目标函数的1阶导，运算量较小，适用于测井响应方程中复杂电阻率响应方程形式。

3 模拟计算

为了进一步验证本文提出的缝洞储集层测井最优化处理方法的稳定性和计算精度，以缝洞型碳酸盐岩储集层中常见的灰岩、云质灰岩地层模型（各地层组分含量见表1）为例进行了模拟计算。根据各类测井曲线的响应方程及响应参数，可计算得到地层模型的理论测井响应值，然后将理论测井响应值及相应的响应参数值作为最优化处理输入信息，对每类地层模型分别进行1 000组随机初始值的计算。

图1、图2分别为灰岩、云质灰岩地层模型地层组分含量的计算结果，结合表 1中的数据进行分析可以发现：本文提出的最优化处理方法受初始值影响较小，对于随机选取的1 000组初始值，均能计算得到最优解，计算结果与模型值基本一致，能够满足测井解释的需要。

表1 灰岩、云质灰岩地层模型各地层组分含量

图1 灰岩地层模型地层组分含量计算结果

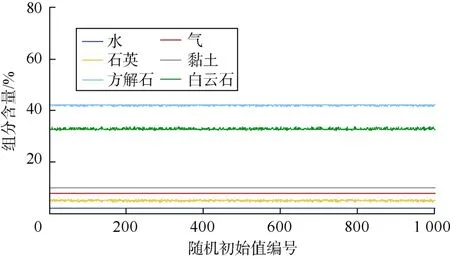
图2 云质灰岩地层模型地层组分含量计算结果

4 实际应用

将本文提出的缝洞储集层测井最优化处理方法编写成处理模块，集成在中国石油新一代测井软件CIFLog1.0中。利用该处理模块对实际测井资料进行了处理，并与传统最优化处理方法计算结果及岩心定量分析结果进行了对比。以某碳酸盐岩储集层 L井测井资料处理为例进行具体说明。

L井所在储集层深度为6 052.6～6 077.4 m，岩性以灰岩为主，取心岩心描述和物性分析表明该段储集层溶蚀孔洞发育。为了进一步确定储集层的岩石物理特性，对该段储集层全直径岩心（见图3a）进行了驱替实验，并分别利用Archie公式与最优饱和度方程对Sw-I实验测量结果进行了拟合，拟合曲线见图3b。由图3b可知，在含水饱和度大于50%时，Archie公式拟合结果与最优饱和度方程拟合结果比较接近，但在含水饱和度较低时，最优饱和度方程拟合效果较好。

图3 L井X号岩心照片及Sw-I拟合曲线

基于Sw-I方程拟合结果，分别使用传统最优化处理方法与本文方法对 L井测井资料进行处理，其中传统最优化处理方法采用Archie公式拟合结果，本文方法采用最优饱和度方程拟合结果，其他地层响应参数均一致。

图 4为利用两种最优化处理方法计算得到的地层方解石、白云石含量与岩心分析结果，图 5为采用两种最优化处理方法计算得到的白云石含量与岩心分析结果间误差分布情况。由图4、图5可知，本文提出的缝洞储集层最优化处理方法的计算结果与岩心分析结果更为接近，计算精度更高。

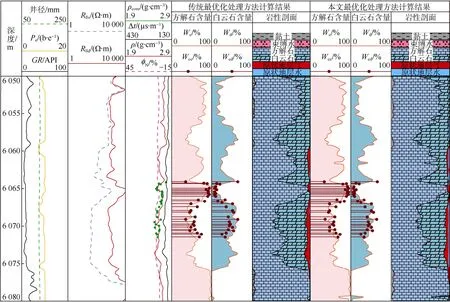
图4 两种最优化处理方法得到的矿物含量与岩心分析结果对比

图5 两种最优化处理方法得到的白云石含量与岩心分析结果间误差分布

将利用两种最优化处理方法计算得到的地层流体组分含量与岩心分析结果（见图6）进行对比后发现：在储集层段，采用本文方法处理得到的含油气饱和度与密闭取心结果吻合度较好，采用传统方法处理得到的含油气饱和度与密闭取心结果相比偏高，两种方法的含油气饱和度相差约10%。以储集层有效厚度20 m、孔隙度6%计算，假设油气藏含油气面积为10 km2，含油气饱和度相差10%相当于油气储量相差1.2×106m3，会对整个油气藏资源评价及开发方案设计产生重要影响。图 7为采用两种最优化处理方法计算得到的含油气饱和度与岩心分析结果间误差分布情况，可以看出，本文方法的计算结果与岩心分析结果更接近。

图6 两种最优化处理方法得到的流体组分含量与岩心分析结果对比

图7 两种最优化处理方法得到的含油气饱和度与密闭取心结果间误差分布

5 结论

本文提出了针对非均质、各向异性缝洞储集层的测井最优化处理新方法。以非均质、各向异性缝洞储集层模型为基础，明确了各测井曲线响应方程形式，最大程度上表达了缝洞储集层地层响应特征。建立了缝洞储集层测井最优化目标函数，并结合惩罚函数法和Levenberg-Marquardt算法求解目标函数，算法具有计算量小、求解效率高的特点。

以灰岩、云质灰岩地层模型为例进行了模拟计算。结果表明：本文提出的最优化处理方法受初始值影响较小，对于随机选取的1 000组初始值，均能计算得到最优解且计算精度高，适用于测井资料评价与解释。

采用本文提出的缝洞储集层测井最优化处理方法与传统最优化处理方法分别进行了实际测井资料处理，并与岩心分析结果进行了对比。结果表明：本文方法计算精度更高，计算结果与岩心分析结果较接近。

符号注释：

Vmi——各骨架矿物的体积分数，%；Vcj——各黏土矿物的体积分数，%；Vw，Vhyd——孔隙水与油气的体积分数，%；Llog——理论测井响应；Pmi——各骨架矿物的测井响应参数；Pcj——各黏土矿物的测井响应参数；Pw，Phyd——孔隙水与油气的测井响应参数；l——骨架矿物种类；n——黏土矿物种类；I——地层电阻增大率；Sw——含水饱和度，%；nb——组合薄片数量；lq——第q个薄片上导电矿物的单元总数；pq，hqk，θqk，b1，b2，b3——待定系数；F——地层因素；a——岩性系数；m——胶结指数；φ——地层总孔隙度，%；φcj——各黏土矿物的孔隙度，%；Rt——地层电阻率，Ω·m；Rxo——冲洗带地层电阻率，Ω·m；Rw——地层水电阻率，Ω·m；Rmf——钻井液滤液电阻率，Ω·m；Sxo——冲洗带含水饱和度，%；tcs——各测井曲线理论测井响应值；fs(v) ——根据地层解释模型建立的各测井曲线测井响应方程；v——各地层组分含量组成的向量；F(v) ——测井最优化目标函数；tms——各测井曲线实际测井响应值；ws——不同测井方法标准化处理因子；nl——测井曲线数目；hr(v) ——地层组分约束条件方程；nc——约束条件数目；cr——约束条件系数矩阵C的第r行；br——约束条件边界；P(v) ——惩罚函数；M——惩罚因子；Φ(v，M) ——无约束问题目标函数；J——矩阵R的Jacobi矩阵；E——单位矩阵；μ——阻尼因子；h——每步的迭代增量；Pe——光电吸收截面指数，b/e；GR——自然伽马，API；Rlls——浅侧向电阻率，Ω·m；Rlld——深侧向电阻率，Ω·m；ρcore——岩心分析密度，g/cm3；Δt——声波时差，μs/m；ρ——岩性密度，g/cm3；φN——中子孔隙度，%；Wc——计算方解石含量（干重），%；Wcc——岩心分析方解石含量（干重），%；Wd——计算白云石含量（干重），%；Wcd——岩心分析白云石含量（干重），%；φc——岩心分析孔隙度，%；Sc——密闭取心饱和度，%；So——计算饱和度，%。

[1]Mayer C.GLOBAL, a new approach to computer-processed log interpretation[R].SPE 9341-MS, 1980.

[2]Quirein J, Kimminau S, La Vigne J, et al.A coherent framework for developing and applying multiple formation evaluation models[C]//Transactions of the SPWLA 27th Annual Logging Symposium.Houston: SPWLA, 1986.

[3]冯国庆, 陈军, 张烈辉, 等.最优化测井解释的遗传算法实现[J].天然气工业, 2002, 22(6): 48-51.Feng Guoqing, Chen Jun, Zhang Liehui, et al.Optimum logging interpretation realizing based on genetic algorithm[J].Natural Gas Industry, 2002, 22(6): 48-51.

[4]邓少贵, 莫宣学, 卢春利, 等.缝-洞型地层缝洞的双侧向测井响应数值模拟[J].石油勘探与开发, 2012, 39(6): 706-712.Deng Shaogui, Mo Xuanxue, Lu Chunli, et al.Numerical simulation of the dual laterolog response to fractures and caves in fracturedcavernous formation[J].Petroleum Exploration and Development,2012, 39(6): 706-712.

[5]李宁.电阻率-孔隙度、电阻率-含油(气)饱和度关系的一般形式及其最佳逼近函数类型的确定(I)[J].地球物理学报, 1989, 32(5): 580-591.Li Ning.General forms of the resistivity-porosity and resistivityoil/gas saturation relations, as well as the determination of their optimum approximating function types (I)[J].Chinese Journal of Geophysics, 1989, 32(5): 580-591.

[6]李宁, 陶宏根, 刘传平.酸性火山岩测井解释理论方法与应用[M].北京: 石油工业出版社, 2009.Li Ning, Tao Honggen, Liu Chuanping.Theoretical method of acidic volcanic logging interpretation and its application[M].Beijing:Petroleum Industry Press, 2009.

[7]李宁.中国海相碳酸盐岩测井解释概论[M].北京: 科学出版社,2013.Li Ning.Introduction to logging interpretation of marine carbonate in China[M].Beijing: Science Press, 2013.

[8]邵先杰, 孙玉波, 孙景民, 等.煤岩参数测井解释方法: 以韩城矿区为例[J].石油勘探与开发, 2013, 40(5): 559-565.Shao Xianjie, Sun Yubo, Sun Jingmin, et al.Logging interpretation of coal petrologic parameters: A case study of Hancheng mining area[J].Petroleum Exploration and Development, 2013, 40(5): 559-565.

[9]高楚桥, 谭廷栋.常见测井响应参数的理论计算[J].石油地球物理勘探, 1997, 32(6): 818-825.Gao Chuqiao, Tan Tingdong.Theoretical computation of ordinary parameters of logging responses[J].Oil Geophysical Prospecting,1997, 32(6): 818-825.

[10]斯伦贝谢公司.测井解释常用岩石矿物手册[M].吴庆岩, 张爱军,译.北京: 石油工业出版社, 1998.Schlumberger.Handbook of common rock minerals in logging interpretation[M].Wu Qingyan, Zhang Aijun, Trans.Beijing: Petroleum Industry Press, 1998.

[11]宁伏龙, 吴能友, 李实, 等.基于常规测井方法估算原位水合物储集层力学参数[J].石油勘探与开发, 2013, 40(4): 507-512.Ning Fulong, Wu Nengyou, Li Shi, et al.Estimation of in-situ mechanical properties of gas hydrate-bearing sediments by well logging[J].Petroleum Exploration and Development, 2013, 40(4): 507-512.

[12]肖立志, 钟兴水.GLOBAL测井解释方法Incoherence函数性质研究[J].石油学报, 1990, 11(2): 49-57.Xiao Lizhi, Zhong Xingshui.Study on the incoherence function in GLOBAL program[J].Acta Petrolei Sinica, 1990, 11(2): 49-57.

[13]高楚桥, 钟兴水.计算岩石矿物成分初始值的极值函数法[J].江汉石油学院学报, 1992, 14(4): 25-30.Gao Chuqiao, Zhong Xingshui.A minimization method to estimate the initial value of matrix content[J].Journal of Jianghan Petroleum Institute, 1992, 14(4): 25-30.

[14]雍世和, 孙建孟.测井数字处理中最优化方法的选择[J].石油大学学报: 自然科学版, 1988, 12(4/5): 11-26.Yong Shihe, Sun Jianmeng.Selection of the optimization method for digital well logging data processing[J].Journal of the University of Petroleum, China: Edition of Natural Science, 1988, 12(4/5): 11-26.

[15]谢刚, 胡振平, 罗利, 等.基于约束最小二乘理论的复杂岩性测井识别方法[J].测井技术, 2007, 31(4): 354-356.Xie Gang, Hu Zhenping, Luo Li, et al.Logging identification of complicated lithology with constrained least square algorithm[J].Well Logging Technology, 2007, 31(4): 354-356.

[16]Madsen K, Nielsen H B, Tingleff O.Methods for non-linear least squares problems[M].Kgs.Lyngby, Copenhagen: Technical University of Denmark, 2004.