基于模糊遗传算法的选矿破碎系统优化控制

吴宇平，章家岩，吴其玲，冯旭刚

基于模糊遗传算法的选矿破碎系统优化控制

吴宇平，章家岩，吴其玲，冯旭刚

矿石破碎是选矿工业流程中的关键环节，破碎过程要求机腔料位稳定，以提高破碎处理流程的工作效率。针对给料机及破碎机具有的惯性、滞后、非线性时变特点，提出了一种基于模糊遗传优化算法的碎矿系统给矿量优化控制策略，控制器采用模糊自适应PID控制算法，并利用遗传算法对控制器参数进行优化，以提高参数在线寻优能力。仿真结果验证了本文提出的优化控制策略的有效性，表明控制系统具有较好的动态品质和较强的抑制干扰能力。

给矿量控制；模糊控制；遗传算法

0 引言

选矿工艺流程包含破碎、筛分、磨矿和分选几个部分，其中破碎工艺是整个流程的初始环节，对选矿质量和产量都起着关键性作用。破碎过程自动化控制的一个主要任务就是实现给矿量的自动调节，以稳定破碎机的机腔料位，从而提高破碎机的破碎处理能力和细碎整体运行效率，使破碎机工作在最佳状态。因此，开发破碎机的给矿自动控制系统具体有极其重要的经济效益和实用价值[1]。

给矿量的多少直接影响着尾矿浓度、溢流浓度及设备的状态。其时间滞后较大，过程干扰因素多，国内选矿行业对于破碎机的运行过程一般采用普通的逻辑控制和安全联锁保护模式，而对于破碎机系统的给料量控制，则通常采用人工手动调整方法[2]，这显然难以满足工程实际的要求。目前工程上采用常规的PID算法来对给料量进行控制[3]，但对于复杂的工况，由于缺乏快速抑制扰动的能力，故难于协调快速性和稳定性之间的矛盾，控制效果不甚理想。文献[4,5,6]针对目前国内磨机运行过程中给矿量控制存在的主要问题,通过对系统的动态特性进行分析, 提出了基于模糊控制理论的Fuzzy-PID 串级控制方案, 并对系统的控制效果进行了仿真研究，取得了一定的效果。文献[7]针对破碎机过程随机干扰因素多、功率控制系统具有强耦合、纯滞后和参数不确定性特点，提出了一种基于神经网络和Smith预估器的模糊PID控制方法，使仿真控制效果得到了明显的改善。在此基础上，任金霞等人又采用自适应控制与模糊PID相结合的方法[8]，应用于圆锥破碎机给矿量控制系统，仿真结果表明，该方法控制性能指标得到明显改善，具有一定的工程应用价值。但通过分析发现，目前这些研究方法对PID参数整定的在线寻优均未进行深入的探讨。为此，本文将遗传算法与模糊PID控制相结合，设计了一种基于模糊遗传算法的选矿破碎系统给矿量优化控制方案，以进一步改善给矿破碎系统的控制品质，提高控制系统的抗干扰能力和鲁棒性。

1 给矿量控制系统基本方案构建

在选矿破碎过程中矿石的大小和硬度极易发生变化，当遇到高硬度的矿石时，破碎机的给料设定值必须实时减少；当矿石小而易碎时，相应地，破碎机的给料设定值必须实时增加，以提高破碎机效率，所以适当地控制送料的速度来补偿矿石体积和硬度的大范围变化很有必要。同时在实际生产过程中，破碎机的容量、胶带的长度不同也会影响到对象的时间常数和纯滞后时间。因此，破碎机的给料量控制系统是一个带有不确定时滞、变参数的大纯滞后系统。

在控制过程中，数字PID控制算法结构简单，是目前工业控制的主流控制算法；加入系统鲁棒性强的模糊控制器，能对具有非线性、时变、多干扰的滞后系统进行有效控制，但考虑到PID初值、量化因子和比例因子对模糊控制器的影响较大，一般由人为设定，而遗传算法能通过模拟自然进化过程搜索最优解，是用于解决最优化的一种比较有效的搜索启发式算法。故本文将遗传算法对模糊控制参数进行优化，并作用于常规的PID控制，从而得到构建碎矿系统中给矿量控制的基本架构如图1所示：

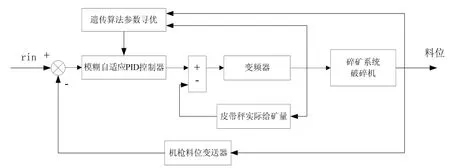
图1 给矿量控制系统基本架构

2 模糊控制器设计

基于模糊逻辑控制的给矿量控制系统框图如图2所示：

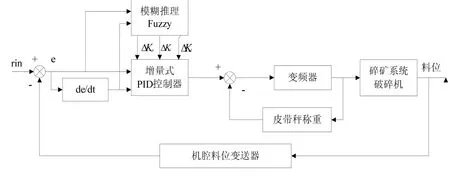
图2 模糊控制系统结构框图

给矿量控制系统的模糊规则表如表1所示：

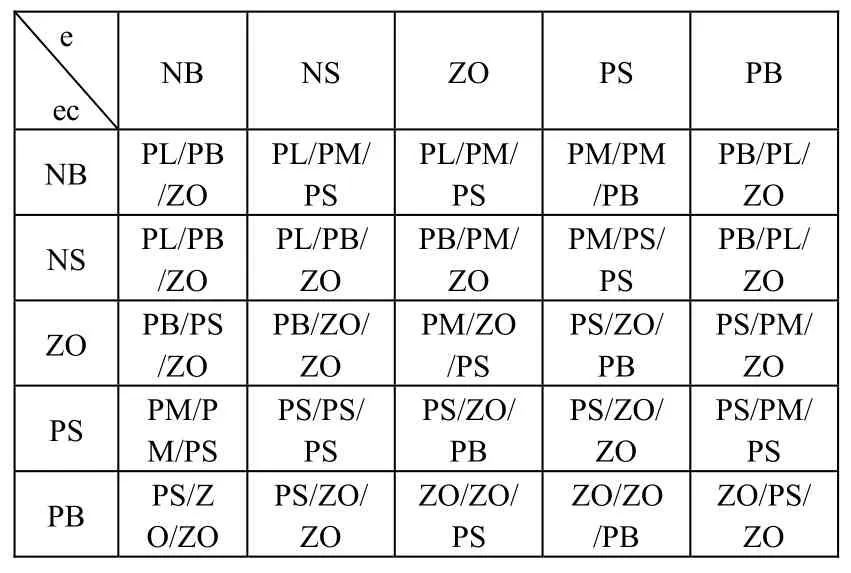
表1 Kp、Ki、Kd模糊控制规则

控制器PID参数初始值及量化因子和比例因子依靠人工设定，不同的参数初值及量化和比例因子会影响控制器的控制效果。根据文献[7]方法建模所得出的对象传递函数为公式（1）：

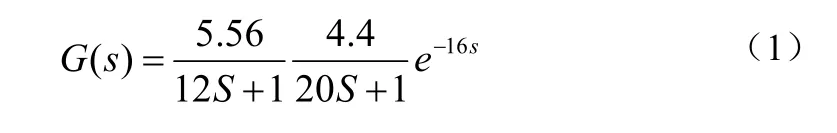
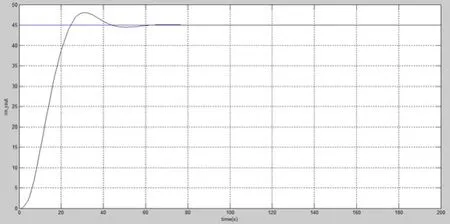
图3 模糊PID控制系统跟踪曲线

该控制系统无稳态误差，总体控制效果比传统PID控制器好，系统响应速度较快，但有超调和衰减振荡存在。

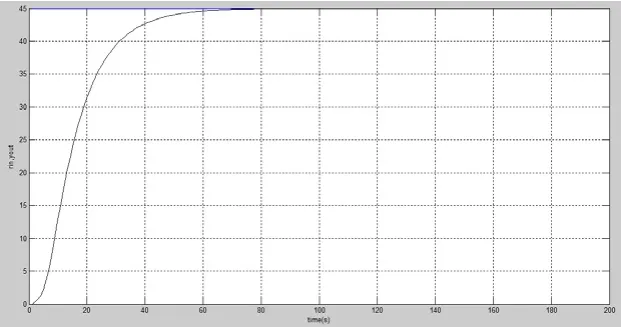
图4 参数修正后模糊PID控制系统跟踪曲线

该控制系统无超调和稳态误差，控制效果比传统PID控制器好，但系统响应速度较慢。由仿真结果可知，模糊自适应PID的控制效果较普通PID有较大的提高，但控制效果受PID初值及量化因子和比例因子的影响较大，而且在控制环节电机的特性也会发生变化，显然若不对这些参数进行优化，控制效果将很难达到最佳，为此设计遗传算法以对参数进行优化。

3 遗传算法参数寻优

遗传算法是一种概率寻优算法，它是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。 其依据生物遗传进化和优胜劣汰的原理，以个体适应度为基础，对个体进行选择、交叉、变异，搜索参数最优解的智能算法。可以对系统的一个或多个参数进行智能优化，优化控制器的控制效果，基本的遗传算法包含初始化、适应度计算、选择、交叉、变异、终止判断等操作[9]。

3.1 编码方法

现有的GA编码方法有：二级制编码、实数编码、Delta编码、自然数编码、格雷码编码、符号编码、链表编码、树型编码、动态变量编码、矩阵编码、量子比特编码等。此处参考文献[10]将遗传算法的编码定为格雷码。由于给矿量料位模糊PID控制器有两个量化因子和3个比例因子，加上PID控制器参数初值，共有8个待寻优参数αe、αec、βp、βi、βd、Kp0、Ki0、Kd0。每个参数采用10位格雷码进行编码，将8个编码后的参数从左到右连接构成长度80位的格雷码基因位串。

3.2 解码算法

将位串个体从位串空间转化成问题参数空间的解码函数如3.1所述，得公式（2）：

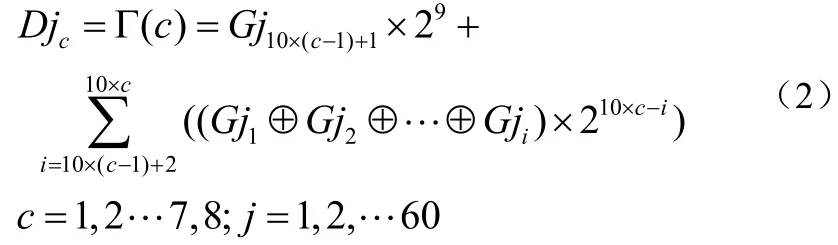
其中Djc为第j个染色体中第c个待寻优参数的十进制表示，Gji为第j个染色体基因格雷码的第i位。

3.3 适应度函数选择

采用误差绝对值时间积分性能指标作为参数选择的最小目标函数。为了防止控制能量过大，在目标函数中加入控制输入的平方项。选用下式作为参数选择的最优指标为公式（3）：

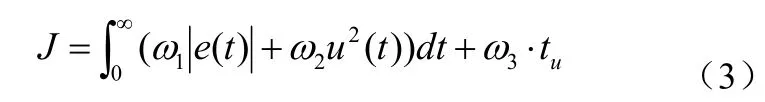
tu为上升时间，w1，w2，w3为权值。

J值越小，控制性能越好，所以选择适应度函数为公式（4）：

3.4 收敛性

参数优化完成后，绘制遗传算法的收敛曲线，如图5所示：

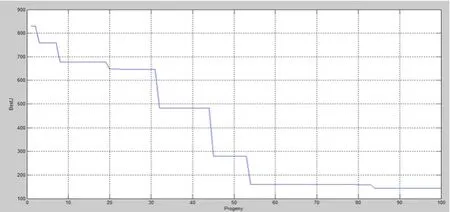
图5 遗传算法单次优化收敛曲线

其中，横轴表示进化代数，纵轴表示跟踪误差均方和。

4 控制效果仿真及分析

在控制器的参数优化中，优化算法的有效性是以建立一个准确的数学模型为基础的。为了单独检验遗传算法的优化效果，应避免模型辨识误差的干扰，因而此处应该用破碎机对象传递函数（如公式1所示）来进行验证，在此基础上利用遗传算法对模糊自适应PID控制器的参数进行优化，并利用Matlab对参数优化效果进行仿真分析。并且，从t=60s至t=120s持续加入阶跃干扰，破碎机给矿量料位跟踪曲线如图6所示：

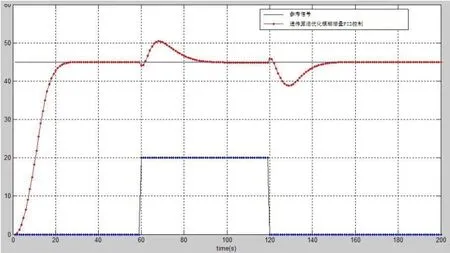
图6 阶跃干扰下料位跟踪曲线

由图6分析可知，系统具有较好的动态特性，超调量小，能够较好地跟踪设定料位参考信号，同时对于干扰具有较好的抑制能力。

5 总结

本文以选矿破碎系统为具体研究对象，针对其存在的非线性大滞后和外负载扰动不确定性等特点，在深入研究选矿破碎系统特性的基础上，选择了给料量控制系统的数学模型，并将模糊遗传控制方法应用于其中。仿真结果表明：基于模糊自适应和遗传算法的给矿量在线寻优控制策略可以对选矿破碎系统进行循环在线建模，并对模糊自适应控制器的参数进行实时的寻优，保证了控制器参数始终为最优值。具有动态响应速度快、超调小、稳定性强等良好的控制品质，能有效地实现快速位置跟踪。控制效果有明显的提高，具有较高的工程应用价值。

[1] 段旭琴等.选矿概论[M].化学工业出版社,2011年2月

[2] 张晓东.先进控制技术在选矿过程控制中的应用研究[D].东北大学1999

[3] 孙福畅.破碎机给料速度自动控制系统的研究与应用[C].第九届中国钢铁年会论文集2013(10)

[4] 谭卢敏.模糊PID控制在球磨机给矿量控制系统中的应用[J].化工自动化及仪表,2011,38(12):1434-1436

[5] 周克良,张建荣.模糊-PID串级控制在磨机给矿量控制系统中的应用[J].煤矿机械,2008,29(2):162-164

[6] 张元华,赵亮,刘强.基于PLC的磨机给矿量智能控制系统[J].硅谷,2011,(9):175-175,166

[7] 任金霞.基于神经网络整定的圆锥破碎机控制系统的模糊预估控制[J].矿山机械,2007,35(4):41-43

[8] 任金霞,郭迎庆.基于模糊自适应PID预估控制的圆锥式破碎机控制系统的研究[J].矿山机械,2005,33(10):42-43

[9] 李士勇.模糊控制、神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.

[10] 余国清,邓锐,雷刚跃.格雷码对遗传算法的改进研究[J].中国科教创新导刊,2007,(12):26-27

[11] 杨丽荣,蔡改贫.基于模糊控制的圆锥破碎机自动控制设计[J].自动化与仪表,2009,24(11):40-43

[12] 刘金琨.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.

Optimal Control of the Crushing System Based on Fuzzy Genetic Algorithm

Wu Yuping, Zhang Jiayan, Wu Qiling, Feng Xugang
（School of Electrical and Information Engineering, Anhui University of Technology, Ma'anshan 243002, China）

Ore crushing is the key link of the beneficiation of industrial processes, the material level of the machine cavity during crushing process is needed to be stable in order to improve the efficiency of crushing process. For mineral crushing system with inertia, hysteresis and nonlinear time-varying, this article proposed control strategies about ore quantity of the crushing system based on fuzzy genetic optimization algorithm. Fuzzy adaptive PID control strategy as a controller, uses genetic algorithms as controller parameter optimization algorithms to improve the performance parameters of on-line optimization. The results of the simulation showed that the control system can achieve higher control accuracy and satisfactory control effect.

Feed Control; Fuzzy Control; Genetic Algorithm

TP273

A

2014.06.27）

吴宇平（1990-），男，安徽工业大学，电器与信息工程学院，硕士研究生，研究方向：复杂工业工程建模与优化控制，马鞍山，243000

章家岩（1963-），男，安徽工业大学，电器与信息工程学院，教授，研究方向：流程工业综合自动化，马鞍山，243000

吴其玲（1989-），女，安徽工业大学，电器与信息工程学院，硕士研究生，研究方向：复杂工业工程建模与优化控制，马鞍山，243000

冯旭刚（1977-），男，安徽工业大学，电器与信息工程学院，副教授，研究方向：智能检测技术及其应用，马鞍山，243000

1007-757X(2014)08-0027-03