基于LMS算法的自适应前馈*
2014-07-25杨黎
杨 黎
(华中科技大学 武汉 430074)
基于LMS算法的自适应前馈*
杨 黎
(华中科技大学 武汉 430074)
作为通信系统核心器件的功率放大器的线性度直接影响了整个系统的通信质量,而前馈线性化技术综合性能较好,一直以来都是研究的热点。论文基于自适应前馈电路的原理,引入了一种改进的LMS算法,通过计算机软件仿真,表明该算法可以很好地改善系统的线性度。
LMS算法; 自适应; 前馈; 相关性
ClassNumberTN713
1 引言
近些年无线通信技术在全世界范围内飞速发展,对传输速率的要求越来越高,通信频段越来越拥挤。为了有效利用频谱资源,无线通信系统广泛采用如QAM和OFDM等具有高频谱效率的线性调制技术。这些信号的包络是变化的,具有较高的峰均比,然而加剧了系统的非线性程度,对处于发射机末端的功率放大器的线性度提出了更高的要求[1]。
常用的功放线性化方法主要分为两类:第一类功放的输入信号是恒包络的信号,如使用非线性器件的线性放大技术和包络分离与恢复技术;第二类功放的输入是包络变化的信号,采用附属电路进行线性化处理消除非线性失真,包括负反馈、预失真和前馈。其中综合比较性能最好的是前馈技术,该技术具有稳定性高、线性改善大和工作带宽较宽等优点,但是对于工作条件的变化比较敏感[2]。由此产生的自适应前馈技术可以自动跟踪和调节环路的特性,保持整个系统性能的长期稳定。
本文采用的自适应算法是LMS算法,并利用ADS和Matlab软件对整个自适应前馈系统进行建模和仿真,仿真结果表明该算法对功放的线性度有很大的改善,可以进行工程应用的研究。
2 自适应前馈电路原理
图1所示为典型的自适应前馈电路的原理图,该电路由误差信号提取环路和误差信号抵消环路组成。在误差提取环路中,输入信号经过耦合器C1之后分成两路信号,上支路信号经主功放放大之后产生主信号和误差信号,然后通过耦合器C2耦合出部分信号,经过衰减器r和矢量调制器VM1之后与下支路经过延时的信号在耦合器C3中进行合成,最后将只得到误差信号,即主功放产生的非线性失真分量。在误差抵消环路中,同样也分为上下两个支路。前面得到的误差信号在下支路经过矢量调制器VM2和误差功放进行线性放大,然后与上支路经过延时后的信号在耦合器C4中进行合成,最后得到的将是消除了误差信号的主信号。当工作条件变化时,控制电路将通过一定的自适应算法对从耦合器C5、C6和C7中耦合出的信号进行处理,分别对两个矢量调制器进行实时控制,从而保持整个系统的稳定。

图1 自适应前馈电路原理图
3 自适应前馈算法
图2所示为自适应前馈电路的简化模型,这里假设耦合器和延时线都是无损耗的,所有耦合器的耦合系数都是1。由于信号的衰减和相移都可以等效为其复包络与一个复数相乘,而任何实数信号都可以用其复包络来表示,为了便于计算机进行处理,这里都将信号用其复包络表示。G(x)是主功放的复数电压增益,它是输入信号瞬时功率的函数。误差功放的复数电压增益记为g。用复系数α和β表示矢量调制器VM1和VM2对幅度和相位的调节。

图2 自适应前馈简化模型
前馈系统的输入信号用Vin(t)表示,则经过主功放非线性放大之后的信号为Va(t),可以表示成线性放大部分和互调失真之和。
Va(t)=Vin(t)G(pin(t))=c*Vin(t)+Vd(t)
(1)
其中c为主功放的线性放大系数,Vd(t)为主功放产生的互调失真信号。
主功放输出信号Va(t)经过衰减器r和矢量调制器VM1后,与下支路信号Vin(t)相减,得到误差信号Ve(t):
Ve(t)=αVa(t)/r-Vin(t)
=(αc/r-1)Vin(t)+α/rVd(t)
(2)
由式(2)可知,当αc/r=1时,则Ve(t)=α/rVd(t),即Ve(t)中将只包含非线性失真信号。Ve(t)通过矢量调制器VM2调节幅度和相位,又经过误差功放线性放大之后,与上支路主功放输出信号Va(t)进行相减,得到最后的输出信号Vo(t):
Vo(t)=Va(t)-βgVe(t)
=[c-βg(αc/r-1)]Vin(t)+(1-βgα/r)Vd(t)
(3)
将αc/r=1带入式(3)可得:
Vo(t)=cVin(t)+(1-βgα/r)Vd(t)
(4)
由式(4)可知,当βgα/r=1时,则Vo(t)=cVin(t),即系统最后的输出将只有线性放大成分。
3.1 相关性最小算法
根据相关性原理,信号间的时域波形相似程度越小,则其相关性就越小。相关性最小算法是根据线性分量和非线性分量之间的不相关特性,来分别判断两个环路中的幅度和相位的匹配情况,并通过自适应算法进行信号处理,实时调节两个矢量调制器,使系统性能达到最好[3]。
在误差提取环路中,下支路信号Vin(t)和误差信号Ve(t)的相关性用ρ1(t)表示:
ρ1(t)=E[Ve(t)Vin*(t)]
=E[(αc/r-1)Vin(t)Vin*(t)+α/rVd(t)Vin*(t)]
(5)
由于Vd(t)和Vin(t)不相关,则E[Vd()t]Vin*(t)]=0。当αc/r=1时,由式(5)可知ρ1(t)=0,即Vin(t)和Ve(t)相关性最小,而此时的条件与上节推出的Ve(t)中只包含非线性失真的条件相同。故可以用Vin(t)和Ve(t)的相关性最小作为误差提取环路的自适应控制准则。
同理,在误差消除环路中,误差信号Ve(t)和最终输出信号Vo(t)的相关性用ρ2(t)来表示,并将αc/r=1和E[Vd(t)Vin*(t)]=0带入可得:
ρ2(t)=E[Vo(t)Ve*(t)]
=E[(1-βgα/r)(α/r)*Vd(t)Vd*(t)]
(6)
当βgα/r=1时,ρ2(t)=0,即Vo(t)和Ve(t)的相关性最小,此时输出信号Vo(t)中将不包含非线性失真分量,与前面的推导结果相同,说明直接功率最小检测法和相关性最小检测法等效,故可以用输出信号Vo(t)和误差信号Ve(t)的相关性最小作为误差消除环路的自适应控制准侧[4]。
3.2 自适应算法
在前馈系统中比较常用的自适应算法是LMS算法。LMS算法是以均方误差达到最小为准则,其根据是最速下降法。最速下降法是一种间接的迭代方法,通过函数的梯度来寻找最优值。由于任一点的函数值沿其负梯度方向下降得最快,故可以利用负梯度方向作为极值搜索方向[5]。
在误差提取环路中,利用Vin(t)和Ve(t)的相关性为零求解αopt,将Vin(t)和Ve(t)的互协方差函数作为模拟梯度函数,即:
σ1=E[Ve(t)Vin*(t)]
(7)
但是它不是实际的梯度信号,不能准确反映负梯度方向,然而它与实际梯度相似,可以跟踪α的最优解。而且在α=αopt时,模拟梯度信号与实际梯度信号都为零。在实际系统中,为了避免求式(7)中的期望,使用无偏估计Dα(t)来代替数学期望,即:
Dα(t)=Ve(t)Vin*(t)
(8)
与求解αopt类似,在误差消除环路中,用Ve(t)和Vo(t)的互协方差函数作为模拟梯度,即:
σ2=E[Vo(t)Ve*(t)]
(9)
而该模拟梯度与实际的梯度信号相同,故可以用来跟踪β的最优解。显然也可用无偏估计来代替,即:
Dβ(t)=Vo(t)Ve*(t)
(10)
将式(8)和式(10)带入传统的LMS算法中,可得关于α和β的迭代算法更新式如式(11)[6]:
(11)
其中a和b为步长因子,决定着α和β的收敛速度。控制电路获取当前时刻的信号Vin(n)、Ve(n)和Vo(n),按照式(11)进行进行信号处理,即可更新到当前时刻的α(n)和β(n),重复该步骤直到稳定收敛。一般α和β的初始值都设为零。LMS算法的收敛速度和步长因子的选取有很大的关系,步长因子越大,则算法的收敛速度越快,但是稳态精度越差,反之亦然,故LMS算法的收敛速度和稳态精度是一对矛盾。为了解决这个问题,本文对α的收敛过程将采用变步长的LMS算法,则α的迭代更新式如式(12)[7~8]:
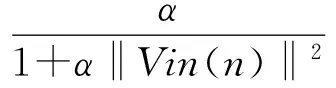
(12)

β(n)=β(n-1)+sign(β)bVo(n)Ve*(n)
(13)
其中sign(β)=sign[Vo(n)Ve*(n)-Vo(n-1)Ve*(n-1)],通过sign(β)来控制调节方向,从而达到β的自适应控制过程。
4 算法仿真与结果分析
本文首先基于ADS软件采用飞思卡尔的MRF6V2300N芯片设计了一个大功率的放大器,并且基于此放大器进行自适应前馈算法的验证。为了在功放输出端得到互调信号,输入将采用频率为260MHz和270MHz的双音信号,功率大小均为27dBm。该功放的输出频谱如图3所示,可以看出输入信号经过主功放后产生了很强的非线性,双音输出47dBm时三阶互调大约在-16dBc左右。

图3 主功放输出频谱
首先利用ADS软件将输入和输出的时域波形存为txt文件,然后调用Matlab中的fopen函数来读取文件中的数据,这里得到的是实数信号信息,而LMS算法中便于处理的是复包络信号,因此需要调用hilbert函数进行希尔伯特变换[10]。接着进行LMS算法迭代,最终得到α和β的稳定收敛值。
α和β的自适应收敛曲线分别如图4和图5所示。α和β的初始值都设为零,并分别按照式(12)和式(13)进行迭代更新。其中步长因子a和b对整个收敛过程的影响很大,在本算法中a=0.000005,b=0.0001。α的实部和虚部大约经过1500次迭代之后收敛,而β的实部和虚部大约经过2000次迭代之后收敛。β的收敛过程明显依赖于α的收敛过程,随着α逐渐趋于收敛,β也将逐渐收敛,故β的收敛速度较α慢。采用新的算法之后,α和β的收敛速度较快,稳态精度也较高。
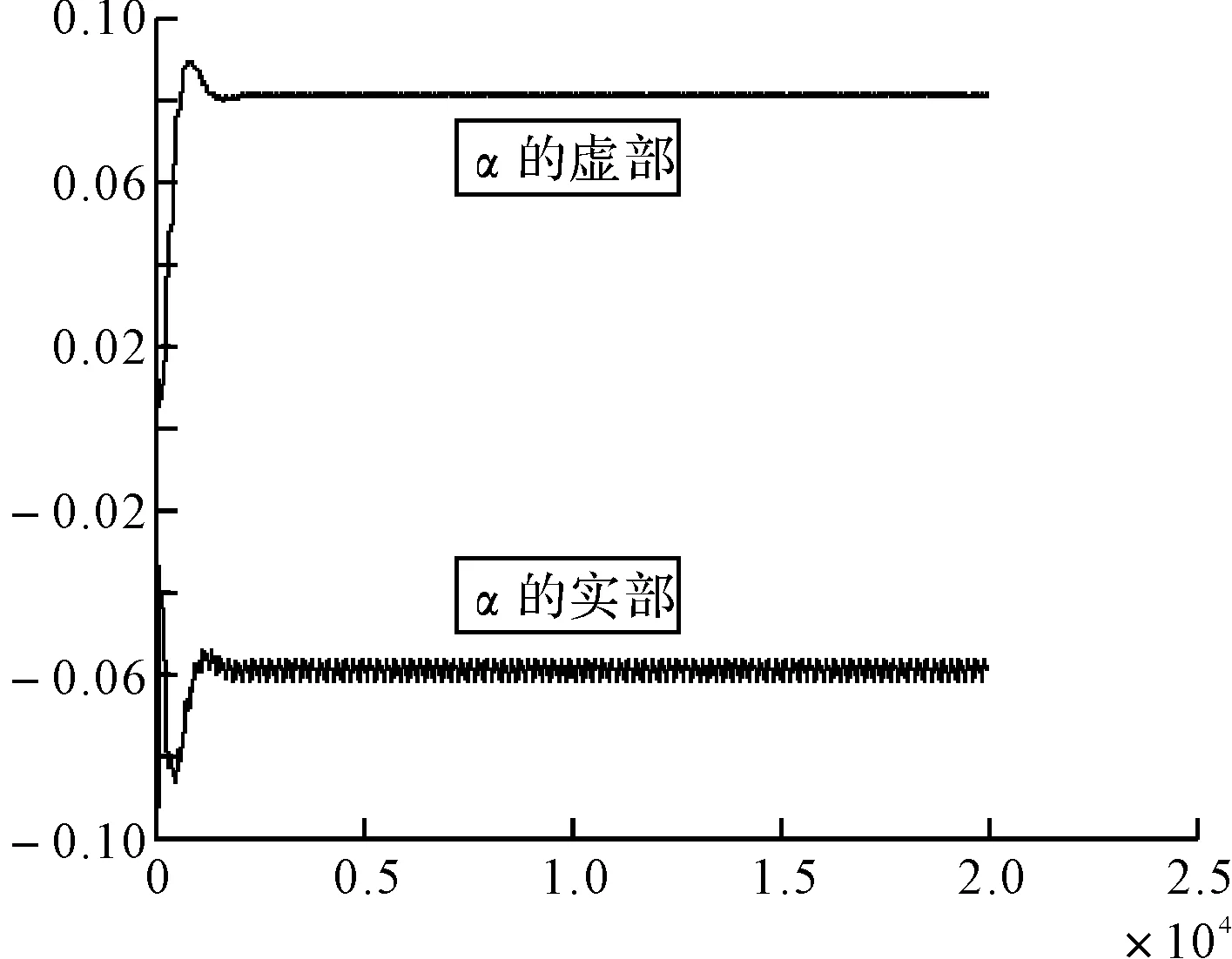
图4 α的收敛过程
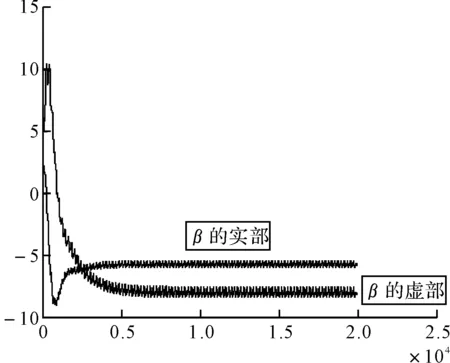
图5 β的收敛过程
图6所示为误差信号的频谱,可以看出主信号已经减小到和互调信号为同一个功率等级,理论上主信号可以被完全消除,但在实际应用中主信号和互调信号处在同一等级即可。由此可见,误差信号提取环路的性能基本上满足了系统要求。
整个前馈系统最后输出信号的频谱如图7所示,可以看出误差消除环路已经把互调信号处理到一个很低的水平,系统的增益达到了20dB,在双音间隔10MHz输出47dBm时三阶互调达到了-46dBc。相对于未加线性化处理的功放,三阶互调改善了30dB左右,由此验证了改进LMS算法的可行性。
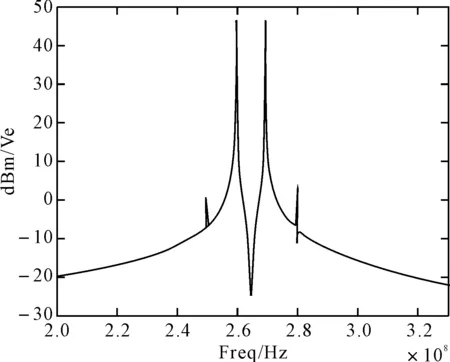
图7 前馈系统输出信号频谱
将α和β最终的收敛值分别带入到两个矢量调制器中,并在ADS中搭建如图2所示的自适应前馈系统电路,仿真结果如图8所示,低端和高端的互调都达到了-46dBc,与Matlab的仿真结果相同,更进一步验证了算法的可行性。

图8 ADS中输出信号频谱
5 结语
LMS算法比较容易实现,性能稳定,收敛速度较快,稳态精度较高,故广泛地应用于自适应前馈系统中。使用LMS算法对前馈系统进行跟踪和调节,可以保持系统长期稳定。
本文对自适应前馈电路的原理进行了详细地分析和推导,引入了一种改进的LMS算法,并对基于ADS设计的功率放大器进行了前馈线性化处理,由Matlab和ADS的仿真结果均可以看出系统的互调达到了-46dBc,比原功放的线性度改善了30dB,由此验证了改进算法的可行性。
[1]郭冰.新型自适应前馈线性功率放大器[D].南京:东南大学,2004:3-7.
[2]M. O. Droma, E. Bertran, M. Gadringer, et al. Developments in Predistortion and Feedforward Adaptive Power Amplifier Linearisers[J]. EGAAS,2005:337-340.
[3]于盛,马洪.前馈功放自适应控制算法性能研究[J].计算机仿真,2007,24(12):320-323.
[4]孙明权.自适应前馈功放控制算法的研究[D].武汉:华中科技大学,2007:26-38.
[5]鲁鹏.自适应前馈功率放大器中控制模块的设计与研究[D].成都:电子科技大学,2010:38-45.
[6]王云飞,王家礼,吕永生.自适应前馈微波超线性功率放大器算法研究[J].西安电子科技大学学报(自然科学版),2004,31(6):948-951.
[7]李存武,林春生.关于几种变步长LMS算法的讨论[J].舰船电子工程,2008,28(5):175-177.
[8]I. Dornean, M. Topa, B. S. Kirei, et al. HDL Implementation of the Variable Step Size NLMS Adaptive Algorithm[J]. Automation, Quality and Testing, Robotics,2008,3:243-246.
[9]刘宪国.前馈线性功率放大器自适应控制系统的设计与FPGA实现[D].成都:电子科技大学,2011:41-44.
[10]李宏.前馈系统中自适应控制部分的研究与设计[D].成都:电子科技大学,2012:31-39.
AdaptiveFeedforwardBasedonLMSAlgorithm
YANG Li
(Huazhong University of Science and Technology, Wuhan 430074)
The linearity of the power amplifier which is the key device of communication system affects the quality of the whole system, and feedforward linearization technology holds good comprehensive performance, so it has always been the research hotspot. A modified LMS algorithm which is based on the principle of the adaptive feedforward circuit is introduced. Through computer simulation software, it can be seen that this algorithm can improve the linearity of the system well.
LMS algorithm, adaptation, feedforward, correlation
2013年10月7日,
:2013年11月27日
杨黎,男,硕士,硕士研究生,研究方向:MMIC设计和大功率功放及其线性化。
TN713DOI:10.3969/j.issn1672-9730.2014.04.010
