基于反加窗和重叠选择的窄带干扰抑制方法
2014-07-25龚文飞
孟 博,龚文飞,孙 昕
(北京交通大学,北京 100044)
1 引言
北斗卫星导航系统(BeiDou navigation satellite system,BDS)是我国拥有自主知识产权的卫星导航系统,但由于北斗卫星导航信号的发射功率低,易受各种信号的干扰。尽管北斗卫星导航信号采用扩频技术,抗干扰能力强,能很好地抑制多种非人为干扰,但是对于高强度的人为干扰,就必须采用相应的抗干扰抑制技术。目前,北斗卫星导航信号的抗窄带干扰技术主要分为时域和频域两种抗干扰技术。时域干扰抑制技术主要是通过设置复杂的时域滤波器来实现对干扰的抑制功能,算法复杂度高,对环境的适应性差。频域干扰抑制技术是将导航信号进行时-频域转换,通过设置干扰门限对干扰信号进行抑制,其算法复杂度显著降低[1-3]。因此,频域窄带干扰抑制方法的研究对北斗卫星导航抗干扰接收机的发展具有重要的实际意义。
2 频域窄带干扰抑制的基本原理
在频域,采用直接扩频技术的北斗卫星导航信号和白噪声都具有平坦特性,而窄带干扰信号能量较为集中,具有明显的频谱峰值。频域窄带干扰抑制的基本原理就是利用北斗卫星导航信号与窄带干扰信号的不同频域特性,从而分离混入北斗卫星导航信号中的窄带干扰信号[4-7]。
频域窄带干扰抑制原理如图1所示。首先对输入的基带北斗导航信号进行N点的快速傅里叶变换(fast Fourier transformation,FFT)。然后通过设置干扰门限,对北斗导航信号进行频域干扰检测,将检测到的干扰谱线直接置零或者衰减至背景噪声大小,实现窄带干扰的频域抑制。最后对干扰抑制后的频域信号进行快速傅里叶反变换(inverse fast Fourier transformation,IFFT),并将其与本地扩频码进行解扩,完成捕获、跟踪以及定位解算等操作,实现定位测速等功能。
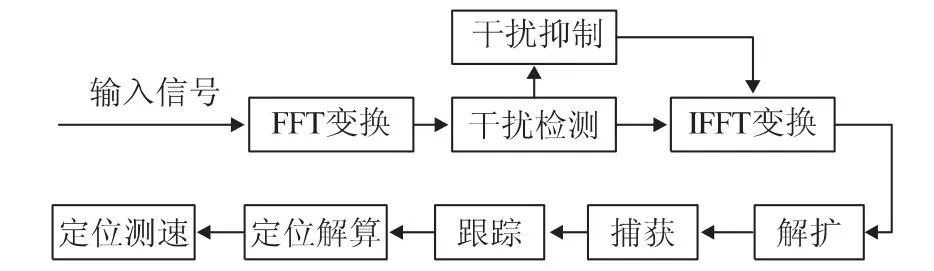
图1 频域窄带干扰抑制原理
3 加窗造成的信号损耗分析
北斗导航时域连续信号s(t)经A/D采样模块后转换为时域离散序列s[k]。对于FFT计算模块而言,其单位时间内只能对2n点离散信号进行时-频域转换,必然存在对序列s[k]进行N(N=2n)点的截断。这种时域序列的截断会造成信号在频域的频谱泄露。假设北斗导航信号中混有强窄带干扰,则该北斗导航信号的频谱泄漏情况如图2所示,在干扰信号峰值谱线附近出现了许多的高频频谱泄露分量。
为了减少信号的频谱泄露,可以采用给信号加非矩形窗的方式,使得截取的信号序列边界变得平滑,减少突然截断造成的信号频谱泄露。信号加窗在减少频谱泄露的同时,也会造成信号的失真,文献 [8]中给出的信号加窗后输出信噪比损失rloss为
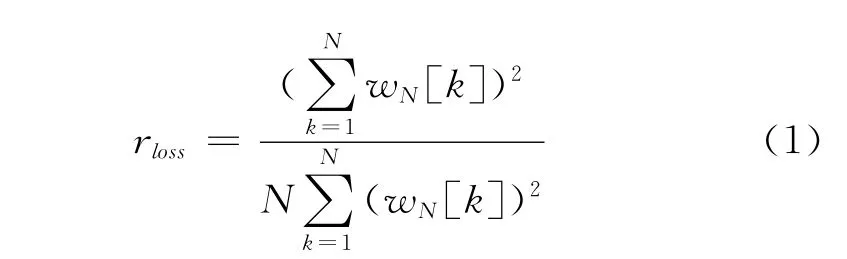
式(1)中,wN[k]为N点的窗函数序列。
取窗函数点数为1 024点,依据式(1),计算不同窗函数的旁瓣衰减以及信噪比损失,其结果见表1。
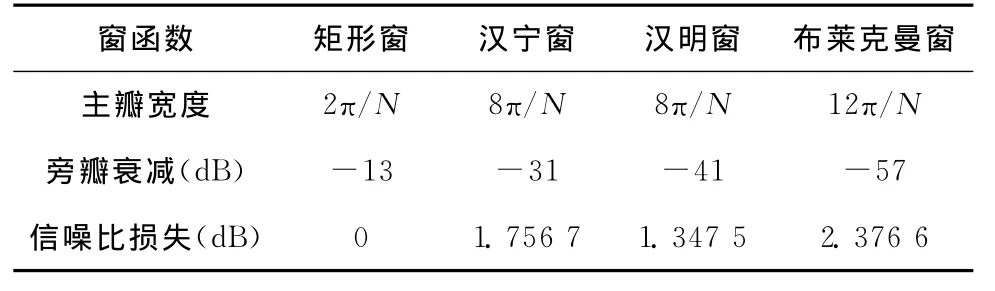
表1 不同窗函数的旁瓣衰减以及信噪比损失
理论结果表明,在高干信比条件下,布莱克曼窗不但能有效减少北斗导航信号的频谱泄露,而且在抑制干扰信号的同时,能有效保留原北斗导航信号。
4 反加窗和重叠选择的组合方法
采用窗函数重叠组合方法可以有效降低因加窗引入的信号信噪比损失[8-9],基于重叠组合的窄带干扰抑制原理如图3所示。首先将接收到的信号序列r(n)分为两路,其中一路信号要进行固定的延迟处理,另一路保持原有的信号不变。然后分别对两路信号进行加窗和FFT变换,将时域信号变换到频域,在频域进行干扰检测和干扰抑制。对干扰抑制之后的信号进行IFFT变换,将频域信号转换成时域信号。最后对两路时域信号进行重叠组合,得到抗干扰以后的时域信号。
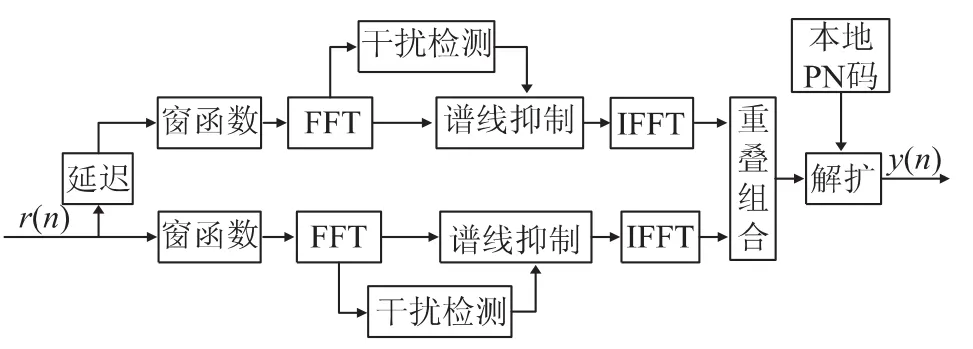
图3 基于重叠组合的窄带干扰抑制原理
窗函数的重叠组合方法分为两种:重叠选择和重叠相加。基于重叠相加算法与基于重叠选择算法的频域窄带干扰抑制原理基本相同,重叠选择算法是将上、下两路输出数据中各取居中的N/2点数据,然后链接起来,形成时域输出序列。重叠相加算法是将重叠选择算法重叠部分的两路信号之间部分直接相加作为干扰抑制之后的时域信号输出。
对于N点窗函数组合算法,假设窗函数的重叠部分为n点,则窗函数的重叠比例η为
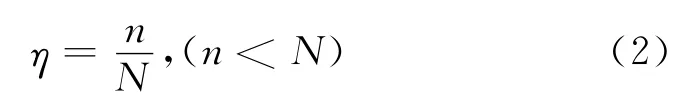
重叠选择算法将两路信号中间部分数据链接,而重叠相加算法将两路信号重叠部分相加,因此重叠相加算法比重叠选择算法增加的运算量C为
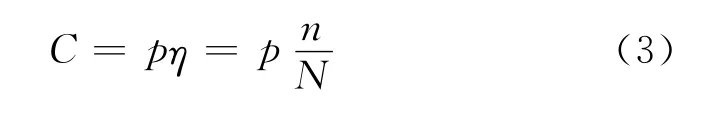
式(3)中,P为一定时间段内处理的导航序列点数。
假设FFT模块一次可以处理N点数据,当两路信号延迟为N/2(即加窗重叠比例为1/2)时,重叠选择造成的信噪比损失rloss_OS和重叠相加造成的信噪比损失rloss_OA分别为[8]
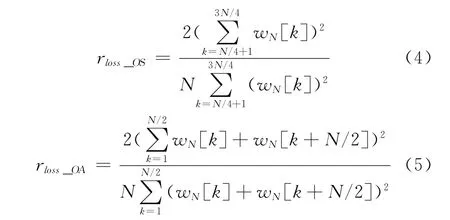
式(4)及式(5)中,wN[k]为N点的窗函数序列。
根据式(4)和式(5),表2给出了不同窗函数和组合方式的信噪比损失。在1/2重叠比例和相同窗函数的条件下,重叠相加所引入的信噪比损失小于重叠选择所引入的信噪比损失。但这种小的信噪比损失是建立在高的计算量的基础之上的。

表2 不同窗函数和组合方式的信噪比损失
窗函数的重叠组合算法可以有效降低加窗造成的信噪比损失,但加窗会造成信号的失真,将直接影响导航接收机的性能。
为了有效解决加窗造成的信号失真问题,可以采用反加窗算法[10]。反加窗算法是在重叠组合算法的基础上,对经过频域干扰检测、干扰抑制、IFFT以及重叠组合后的信号,乘以窗函数权值的倒数,通过这种方式来恢复时域信号。
假设混有窄带干扰的导航信号序列r[k]为
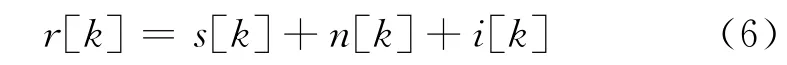
式(6)中,i[k]为窄带干扰序列,n[k]为加性白噪声序列,s[k]为导航信号序列。
导航信号序列r[k]经频域干扰检测、干扰抑制、IFFT以及重叠组合过程,得到信号r′[k]为

式(7)中,w′[k]是与重叠组合方式对应窗函数的部分数据,对于重叠选择方式有
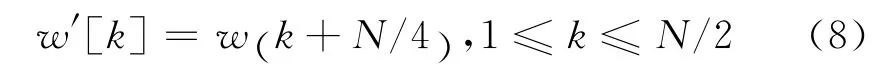
对于重叠相加方式有
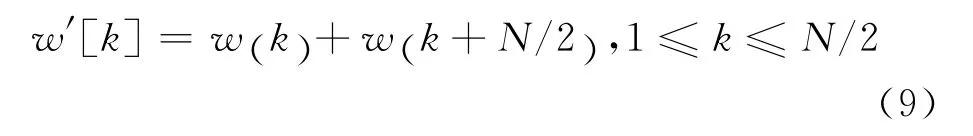
对信号r′[k]进行反加窗操作,即乘以窗函数剩余部分w′[k]权值的倒数,可得反加窗后信号R[k]为
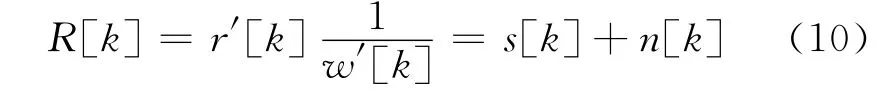
式(10)中,w′[k]为完整窗函数w[k]的中间部分,避免了w′[k]取0。
比较式(6)和式(10)可见,通过反加窗算法,可以完全恢复原来的时域导航信号,消除因加窗带来的信噪比损失。
在相同重叠比例条件下,重叠相加算法优于重叠选择算法,但是重叠比例的增大以及选择重叠相加算法意味着算法计算量的增大,这是在利用大的计算量来换取小的信噪比损失。反加窗算法不限制窗函数和重叠组合方式,即无论选择重叠相加方式或重叠选择方式,在对导航信号反加窗后,都能够快速的恢复原导航信号,消除了因加窗带来的信噪比损失。因此,在采用反加窗算法后,就无需选用较大的窗函数重叠比例和计算量大的重叠相加算法来改善信噪比。相比重叠相加与反加窗的组合方式,重叠选择与反加窗的组合方式减少了计算量。
图4示出了导航信号加窗、重叠选择加窗以及反加窗时域波形,窗函数采用布莱克曼窗,重叠比例为1/2,可见直接加窗造成了严重的时域信号畸变。经窗函数重叠选择后的时域信号仍存在一定程度的信号失真。信号经反加窗后完全得到了恢复,消除了因加窗引入的信号失真。这一结论同上面进行的理论推导是一致的。
为了进一步说明 “重叠选择+反加窗”方法的优越性,现与以下三种可能的组合方法进行比较说明。方法一:“(一路数据)加窗+频域干扰抑制+反加窗”,方法二: “(两路数据)加窗+频域干扰抑制+重叠选择”,方法三: “(两路数据)加窗+频域干扰抑制+重叠相加”。
方法二、方法三省略了反加窗,因而无法消除加窗造成的信噪比损失。方法一省略了重叠组合,直接对干扰抑制后的信号反加窗,会引发数值不稳定、硬件实现量化误差大的问题。原因在于:此时的反加窗是与窗函数wN[k]权值的倒数做乘法运算,然而窗函数wN[k]边缘数值过小(还存在零值和负数的情况),对其取倒数存在数值过大等问题。
考虑到:(1)重叠组合的窗函数w′[k]不存在边缘数值过小问题,相应的反加窗不会引发数值过大问题;(2)重叠选择算法的计算量小于重叠相加算法。因此,综合最优的干扰抑制方式为 “(两路数据)加窗+频域干扰抑制+重叠选择+反加窗”方式。
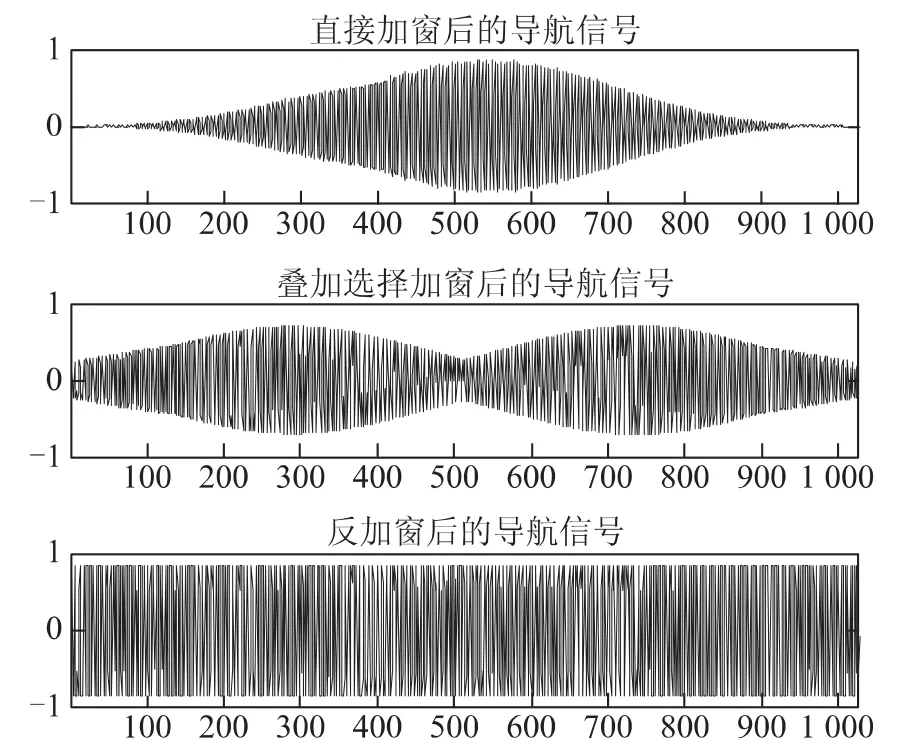
图4 导航信号加窗、重叠选择加窗以及反加窗的时域波形图
5 仿真结果
结合图3给出的基于重叠组合算法的频域窄带干扰抑制原理,使用MATLAB进行了性能仿真,并在现场可编程门阵列 (field programmable gate array,FPGA)上进行了硬件功能实现。仿真条件如下:选用1 024点窗函数和FFT计算模块;延迟512点,既窗函数重叠比例为1/2;采用反加窗算法和计算量低的重叠选择方式;干扰信号是干信比为60dB、信噪比为-30dB的单音干扰,导航信号是码速为10.23MHz的P码,功率为80 dBm,量化为10bit位。
窄带干扰抑制前的信号频谱如图5所示,峰值谱线是干信比为60dB的单音干扰信号,由于导航信号是实信号序列,因此其频谱呈对称性。在干扰抑制前,导航信号完全被湮没在干扰信号中。窄带干扰抑制后的信号频谱如图6所示,通过设置干扰门限,将检测到的干扰谱线直接置零后,信号谱线中没有了明显的频谱峰值,即具有峰值频谱特性的窄带干扰信号得到了抑制。
理论分析表明,北斗卫星信号经反加窗运算后完全得到了恢复,消除了因加窗和重叠组合引入的信噪比损失,因此,反加窗加重叠选择方式和反加窗加重叠相加方式在抑制窄带干扰信号的能力上是一致的,但采用反加窗加重叠选择能够减少系统的计算量。
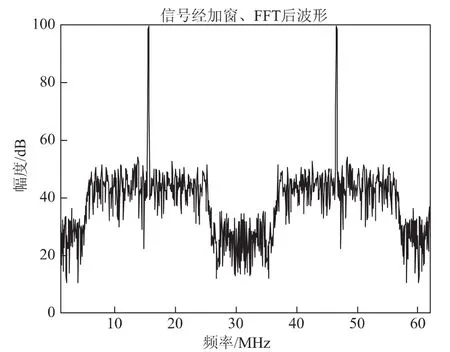
图5 干扰抑制前的信号频谱
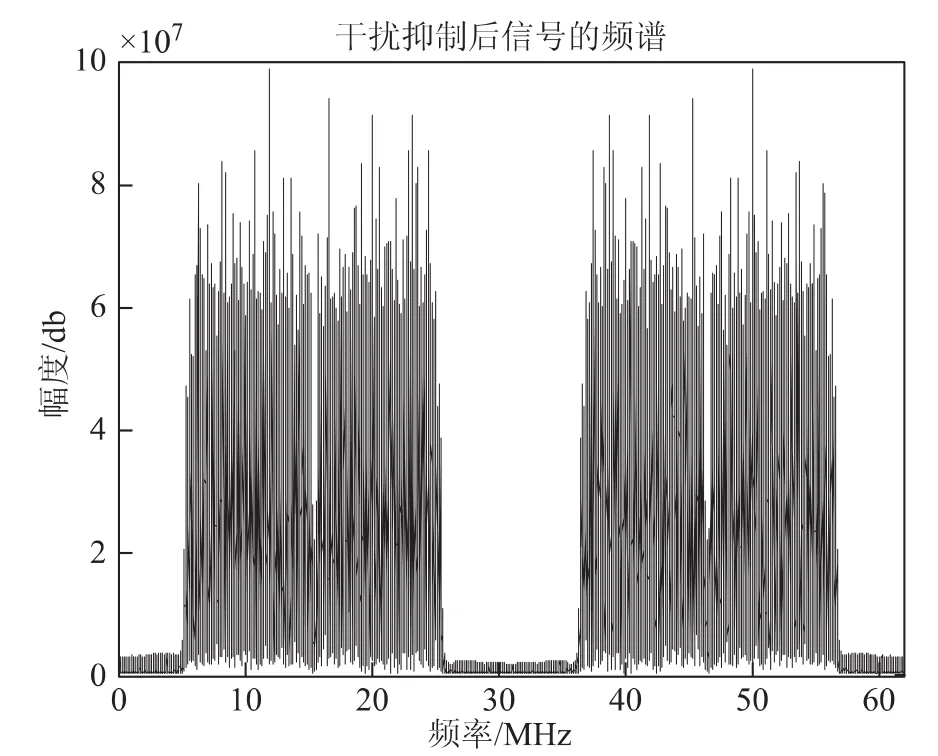
图6 干扰抑制后的信号频谱
6 结束语
基于北斗接收机的频域窄带干扰抑制技术,重点分析了窗函数的重叠组合算法和反加窗算法,并对相应的算法进行了理论分析和性能仿真。理论分析表明,反加窗算法不限制窗函数的类型和重叠组合的方式,即无论选择何种窗函数和组合方式,在对导航信号反加窗后,都能够快速的恢复原导航信号,消除了因信号加窗造成的信噪比损失。同时,重叠相加算法的计算量大于重叠选择算法,在采用反加窗算法后,就无需选用计算量大的重叠相加方式来改善信噪比,因此,相比重叠相加与反加窗的组合方式,重叠选择与反加窗的组合方式在有效抑制窄带干扰信号的同时降低了系统的计算量。
[1]MILSTEIN L B.Interference Rejection Techniques in Spread Spectrum Communications[EB/OL].[2013-08-21].http://www.dragonwins.com/domains/getteched/bbc/literature/milstein88.pdf.
[2]LI Ke,HOU Chun-ping,HOU Yong-hong,et al.New Cooperative Frequency Domain Differential Modulation and Demodulation[J].Journal of Systems Engineering and Electronic,2011,22(6):892-896.
[3]AMIN G M.Interference Mitigation in Spread Spectrum Communication Systems Using Time-frequency Distributions[J].IEEE Transactions on Signal Processing.1997,45 (1):90-101.
[4]冯冀宁,吴嗣亮,姜伟.DSSS窄带干扰抑制滤波器性能研究与比较[J].北京理工大学学报,2010,30(6):727-731.
[5]来庆福,赵晶.斜投影极化滤波的雷达导引头抗箔条干扰方法[J].信号处理,2011,27(7):1016-1021.
[6]KETCHUM J,PROAKIS J.Adaptive Algorithms for Estimating and Suppressing Narrow Band Interference in PN Spread-spectrum Systems[J].IEEE Transactions on Communications,1982,30(5):913-924.
[7]BORIO D,CAMORIANO L.Impact of GPS Acquisition Strategy on Decision Probabilities[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(3):996-1011.
[8]曾祥华,李峥嵘,王飞雪.扩频系统频域窄带干扰抑制算法加窗损耗研究[J].电子与信息学报,2004,26(8):1276-1281.
[9]龚文飞,孙昕.卫星导航接收机时域窄带干扰抑制滤波器设计与性能分析[J].信号处理,2011,27(11):1774-1779.
[10]杨晓波,王薇.一种扩频系统频域干扰抑制稳健加窗方法研究[J].传输与接收,2011,35(7):128-131.
