基于E-S方法的齿轮系故障信号辨识技术研究*

毛向东，袁惠群 ，孙华刚

(1.东北大学，辽宁 沈阳 110819； 2.军械技术研究所，河北 石家庄 050000)

基于E-S方法的齿轮系故障信号辨识技术研究*

毛向东1,2，袁惠群1，孙华刚2

(1.东北大学，辽宁 沈阳 110819； 2.军械技术研究所，河北 石家庄 050000)

针对齿轮系早期故障信号弱，特征不明显的问题，提出一种基于经验模态分解(EMD)与奇异谱分析(SSA)相结合的故障特征信号辨识方法。通过对信号分解和特征筛选，重组轨道矩阵，实现对不同特征信息的提取和识别。试验表明该方法不仅有效提取出了系统的故障特征信息，而且实现了对系统状态和微弱故障信息的有效识别。

特征提取；信号辨识；经验模态分解；奇异谱分析

Abstract: For the question of signal being weak and feature invisible in early stage of failure gearbox，an identification method of failure feature for the mechanical vibration system based on empirical mode decomposition (EMD) and singular spectrum analysis (SSA) is found. With E-S method, the signal is decomposed, the characteristic is selected, and the attractor orbit matrix can be obtained. And the different diagnostic information of the vibration signal can be extracted with the orbit matrix recombination. It is proved by test that the method can not only effectively extract the characteristics of the system, but also effectively recognize and identify the weak failure characteristics and failure status for the gearbox system.

Key words: feature extraction； signal identification；EMD；SSA

0 引 言

齿轮系广泛应用于兵器、车辆、船舶、矿山、工业机械等大型装备、设备中，多在高强度、超高速、大负载状态下运行。由于齿轮系自身结构复杂性和工作环境恶劣等原因，引发齿轮失效，对装备平稳运行带来安全隐患，严重时导致装备和人身安全事故，因此旋转机械的早期故障预报对避免安全事故发生有重要的现实意义。故障预报主要采取状态监测手段进行，一般通过故障信号获取、故障特征提取和模式识别途径实现故障诊断。但在实际工况下，齿轮系在强背景噪声下工作，有效信噪比低，信号特征微弱，状态信号识别难。

传统的信号测试一般是通过频谱分析、相关分析、时间序列分析、自适应消噪[1]等手段从背景噪声中检测出有用信号，随着信号检测技术的不断发展，出现了诸如小波消噪[2]、混沌阵子[3]、盲源分离[4]、随机共振[5]、经验模态分解[6]等信号处理方法，这些方法在一定程度上实现了对检测信号的特征提取，但对于噪声污染严重的检测信号，由于信号成分较弱而被淹没于其它成分之中，很难完全剥离，致使信号特征信息难以获取。

笔者针对强背景噪声下，齿轮故障特征难提取和辨识问题，提出了基于经验模态分解(EMD)与奇异谱分析(SSA)的微弱信号提取方法(简称E-S方法)，对试验齿轮箱振动信号进行故障特征提取，验证了E-S方法的有效性。

1 E-S方法简介

1.1 基本原理

E-S方法基本原理如图1所示，先将信号进行EMD分解提取IMF分量，利用SSA对信号进行奇异值分解和重构，并对无关分量的剔除实现对微弱特征信息的提取。EMD分解有两种结果：一是信号可以分解出特征明显的IMF分量；二是难以分解出特征明显的分量，难以对信号进行深入分析。对于难分解信号先利用奇异值分解降低噪声成分干扰后，再进行EMD分解可获得特征较为明显的IMF分量。对于分解得到的特征明显的IMF分量，利用由奇异谱增量分析筛选出的奇异值对信号进行重构，即可获得理想降噪效果的信号。

具体算法原理步骤如下：

①利用EMD算法对测试信号进行分解，在对各IMF分量频谱分析的基础上，提取包含信号特征频率的IMF分量；②若提取到IMF分量中特征频率占主要成分，则对该分量进行SSA分解，提取包含特征信息的主要奇异值成分，再利用SSA逆算法进行信号重构，实现对特征成分的提取；③若经EMD分解后，信号特征频率成分仍然淹没在噪声成分中，则先对原始信号进行奇异值分解，剔除信号中的噪声干扰成分，增强信号的特征频率成分；④利用步骤①、②对增强信号进行特征成分提取；⑤对得到的特征增强的信号特征成分进行信号重构，即可得到干扰噪声有效剔除后的测试信号。利用相关的诊断方法即可对系统进行状态分析。

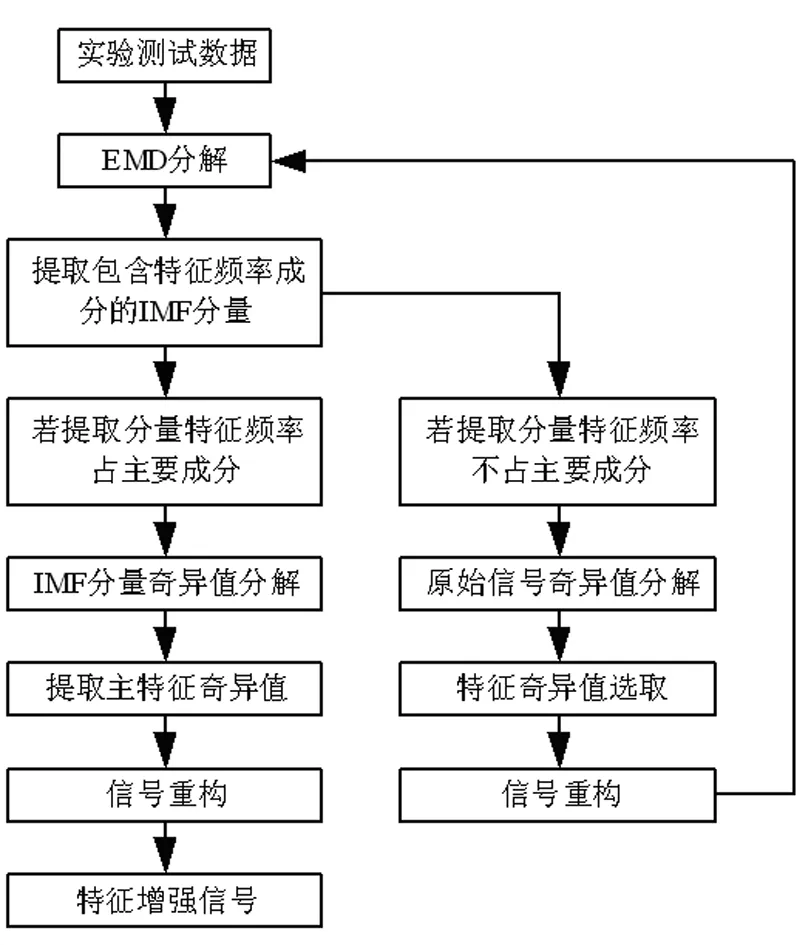
图1 信号特征提取算法原理框图

1.2 特征信号算法

EMD将复杂的信号分解为有限阶IMF分量，每阶IMF分量所包含的频率成分随信号本身变化而变化。对于任意一维时间序列x(t)，通过EMD可以分解出包含并突出了原信号的局部特征信息的n阶IMF。

(1)

式中：xk(t)为原信号的中心趋势，yi(t)分别包含了信号从高到低不同频率段的成分，使得在某阶IMF分量中微弱成分可以较明显的表现出来。因此，问题的关键是在n阶分量中选取感兴趣的IMF。目前，对于机器设备正常运行的频率及故障时的频率都是已知的，在这样的情况下，只需对n阶IMF分析频率成分，从而找到含有故障频率的IMF分量yr。

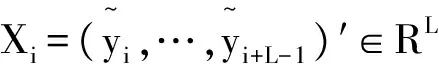
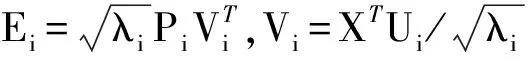
(2)

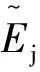
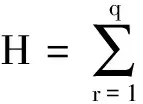
2 仿真分析

由式(3)产生一组时间序列，其中含有强噪声干扰。仿真信号如图2所示。

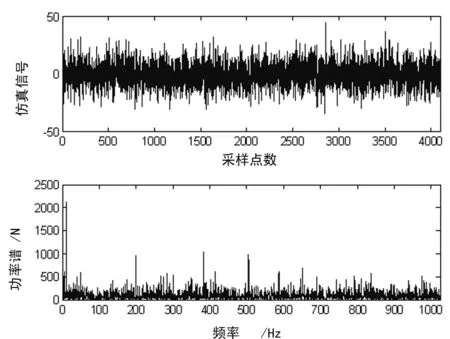
图2 仿真信号

x(t)= sin (2πf1t)+sin (2πf2t)

+10randn(1,M)

(3)

式中：f1=10 Hz，f2=200 Hz，采样频率fs=1 000 Hz，采样时间Ts=2 s，M为时间序列t长度。

信号中包含10 Hz和200 Hz两个特征频率成分，并含多种强干扰成分，严重干扰和制约着信号特征成分的有效提取。信号降噪过程目的就是剔除背景噪声成分，有效获取特征信号成分。其过程如下。

2.1 EMD信号分解

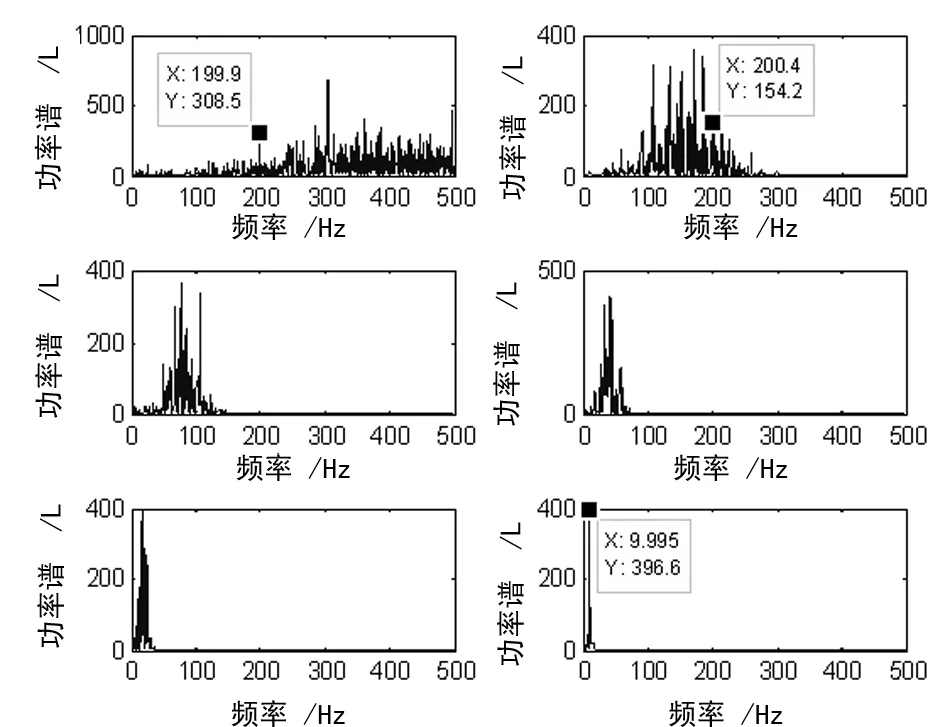
图3 IMF频谱图

2.2 特征信号提取与处理

(1) 10 Hz特征频率成分提取

对第6阶分解阶次对应的特征信号10 Hz的特征成分进行SSA分析，噪声干扰得到了较好的剔除，分解结果如图4所示。

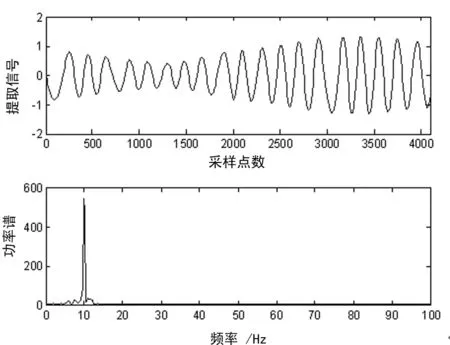
图4 10 Hz特征频率

(2) 200 Hz特征频率成分处理与提取

① 特征增强：通过对信号奇异值特征提取，并重构信号，可实现信号在200 Hz特征频率成分处的特征增强。

② 过程分析：对处理后信号进行EMD分解，由分析可看出，对应200 Hz的特征频率成分很难被完整的分解处理，分解结果包含较强的伴随成分。

③ 干扰剔除：对步骤②得到的信号进行奇异值分解，特征信号中的干扰成分得到进一步的降低。根据这一原理，经过数次奇异值分解和特征提取后，可有效剔除特征成分中的干扰成分如图5所示。

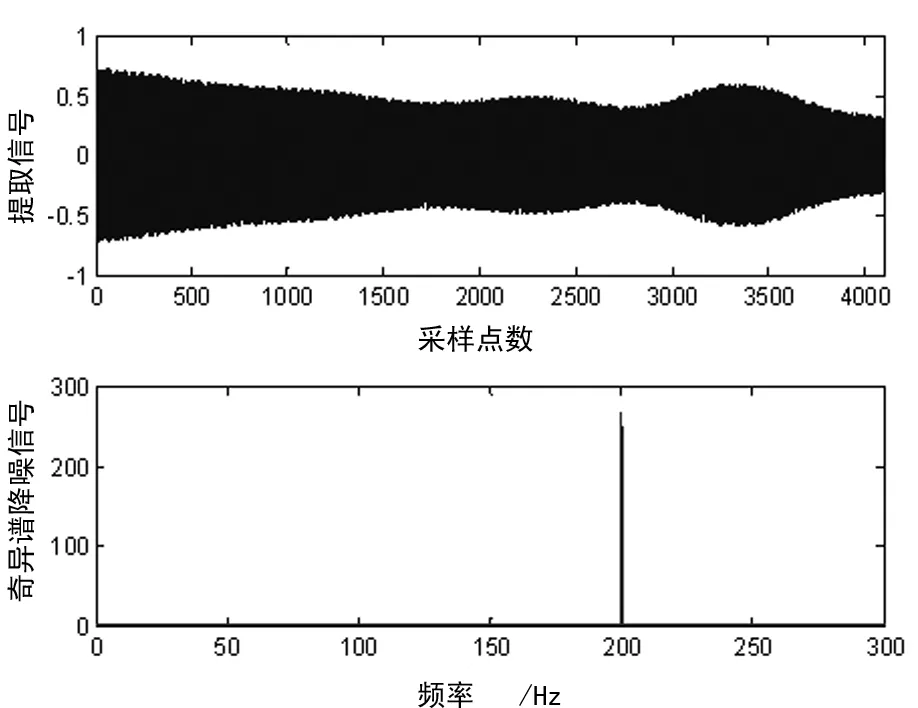
图5 200 Hz特征频率

(3) 信号重构

将提取的信号的特征成分进行重构，如图6所示，由图可以看出，经过上述处理过程，有效提取出了信号的特征频率成分。

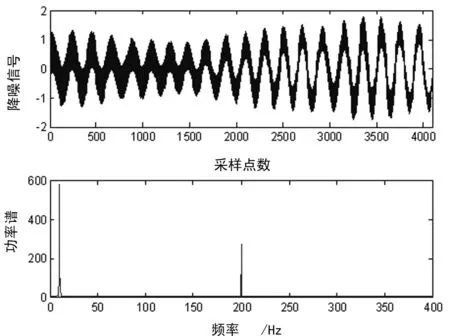
图6 降噪信号

3 实验验证

3.1 信号采集

采用图7所示实验台验证E-S方法的可行性。试验分别获得转速720 r/min下正常运行和裂纹故障两种状态下的振动信号，齿轮特征频率如下：f主=12 Hz，f从=8.8 Hz，f啮合=660 Hz。两种情况下的波形及频谱特性如图8所示，395 Hz附近和1 500～2 000 Hz之间的频率成分，完全淹没了齿轮传动系统的特征成分。

图7 齿轮减速箱实验平台

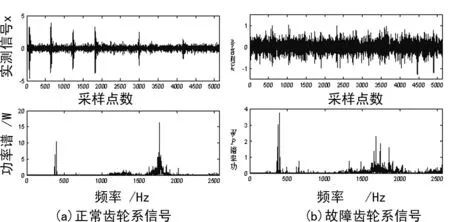
图8 齿轮信号的波形图及频谱图

3.2 信号处理

(1) 特征提取目标确定

齿轮系正常运行中，特征频率确定为被测齿轮的旋转频率及啮合频率。

(2) 正常齿轮特征分量确定

对测试信号进行EMD分解，前4阶主IMF分量的频谱图如图9所示。从图中可看出，系统的啮合频率被淹没在第3个IMF中。

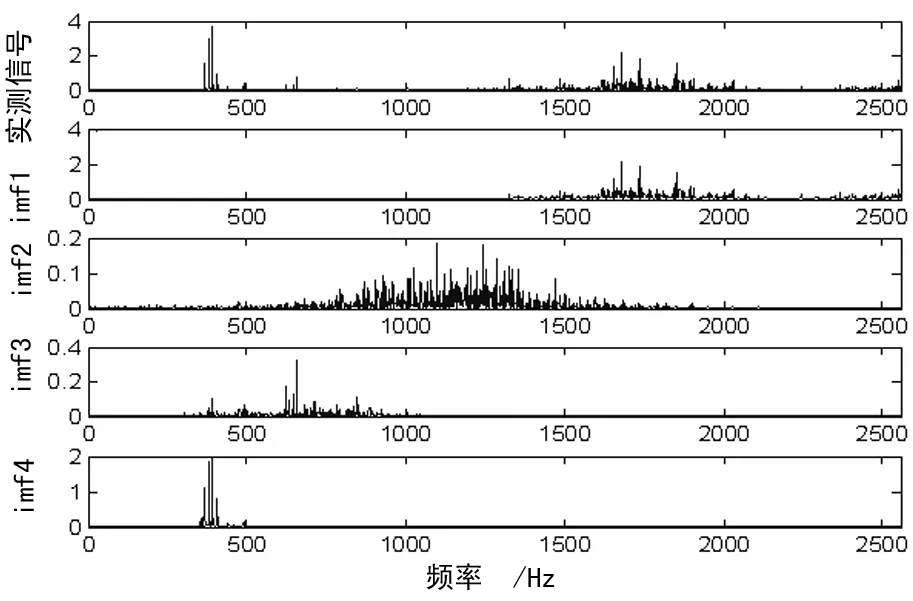
图9 正常齿轮信号的主IMF分量频谱图

对第3个IMF进行奇异值分解，保留前2阶奇异值进行信号重构，得到降噪后的正常齿轮系统信号，如图10所示。由降噪信号的频谱图可看出，降噪后信号的频率成分主要集中在657.1 Hz及伴随频率621.1 Hz、633.1 Hz、645.1 Hz处，这些频率之间的间隔为12 Hz，对应着齿轮箱主动轴的转频，表明传动系统冲击频率主要是由输入轴作用在齿轮传动系统上产生的。另外由于试验台电机转速是通过电流调节进行控制的，系统转速读取存在一定的误差，因此频率657.1 Hz对应着齿轮的啮合频率。

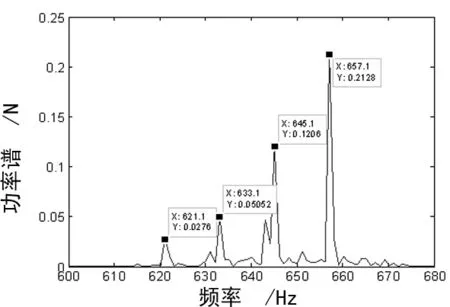
图10 奇异值分解降噪信号

(3) 故障齿轮特征分量确定

当齿轮存在故障时，不同的故障程度可能使得信号中存在其他特征频率及边频成分。图11为裂纹故障信号的主IMF分量频谱图。从图中可看出系统的啮合频率被淹没在第3个IMF中。利用正常齿轮信号特征提取方法无法有效提取信号状态特征。需降低强噪声对实测信号的干扰，放大信号的有用信息。

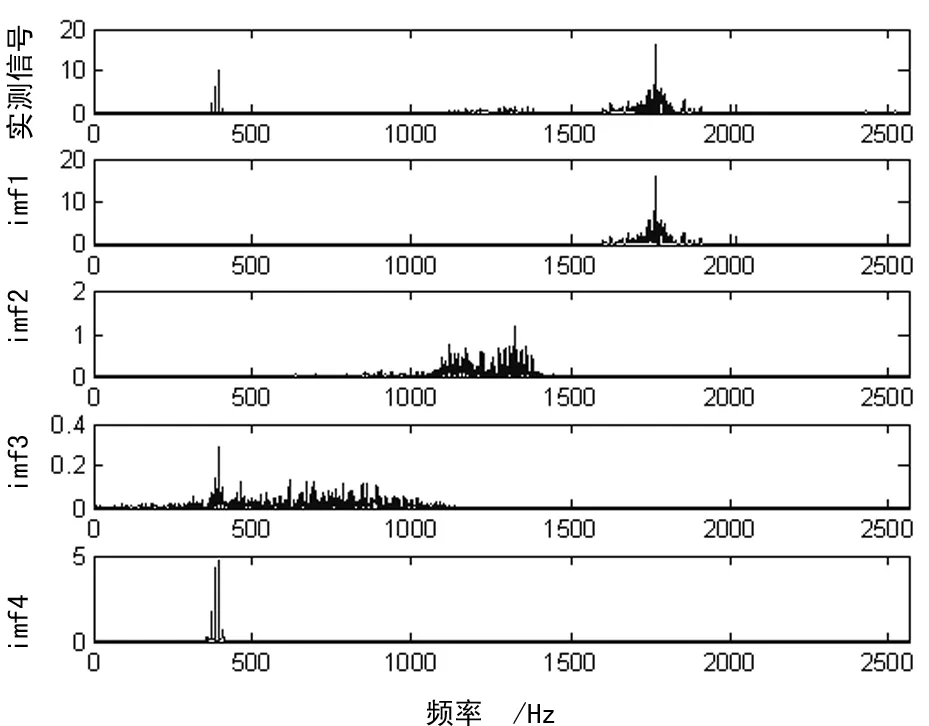
图11 齿轮故障信号的主IMF分量频谱图

对于裂纹故障信号，通过去除信号的前15阶奇异值可降低噪声干扰对齿轮系统的影响，实现了系统的信号特征成分增强。在此基础上，对处理信号进行EMD分解，提取包含系统特征成分的IMF分量，并对其进行奇异值分解，提取前4阶奇异值进行信号重构，实现信号的合理降噪和特征成分提取，提取后信号频率特征如图12所示。经过上述过程处理，有效提取出了系统的啮合频率657.1 Hz，而在啮合频率附近产生的主要边频与啮合频率之间的间隔以9 Hz为主，对应着故障齿轮的转频。由此表明，传动系统信号以故障轮的转频及啮合频率为主，特征信息主要来源于故障轮。

图12 齿轮故障信号的特征信息

4 结 语

提出了一套基于E-S方法诊断齿轮系设备故障的方法。通过EMD和SSA相结合进行信号处理，可实现强背景噪声下对信号特征信息的有效提取，在实现降噪的同时，还保留了信号原空间的主要特征。通

过实验，验证了笔者所建立方法的合理性和有效性，为设备故障信号的有效提取和状态识别提供了一种新的方法。

[1] 刘世金，张榆锋. 在噪声抵消应用中自适应滤波算法性能的仿真比较 [J]. 系统仿真学报,2006, 18(5):1178-1180.

[2] 吴 芳，杨日杰. 基于相关与小波变换相结合的弱信号检测 [J]. 海军航空工程学院学报,2008, 23(1):26-28.

[3] 汪芙平，王赞基. 混沌背景下信号的盲分离 [J]. 物理学报,2002, 51(3):474-481.

[4] 季 忠，金 涛. 基于独立分量分析的消噪方法在选择机械特征提取中的应用[J]. 中国机械工程,2005, 16(1):50-53.

[5] 冷永刚，王太勇. 基于双稳类随机共振的信息检测 [J]. 电子与信息学报,2005, 27(5):734-739.

[6] WU Z, HUANG N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J]. Proc.R.Soc.London, Ser.A. 2004(460):1597-1611.

[7] Alonso F J, Castillo J M. Application of Singular Spectrum Analysis to the Smoothing of Raw Kinematic Signals[J]. Journal of Biomechanics，2005，38(5):1085-1092.

[8] Hossein Hassani, Mohammad Zokaei. Does Noise Reduction Matter for Curve Fitting in Growth Curve Models?[J]. Computer Methods and Programs in Biomedicine,2009, 96:173-181.

Research on Signal Identification Technology for Failure Gearbox with E-S Method

MAO Xiang-dong1,2，YUAN Hui-qun1， SUN Hua-gang2

(1.NortheasternUniversity,ShenyangLiaoning110819，China； 2.OrdnanceTechnologyResearchInstitute,ShijiazhuangHubei050000，China))

2014-06-23

毛向东(1973 -)，男，山西和顺人，高级工程师，博士，研究方向：装备保障工程、装备测试技术研究。

TP391

A

1007-4414(2014)04-0042-05