航空发动机推力销载荷计算及应变分析*

雷晓波，张 强， 张永峰

(中国飞行试验研究院，陕西 西安 710089)

航空发动机推力销载荷计算及应变分析*

雷晓波，张 强， 张永峰

(中国飞行试验研究院，陕西 西安 710089)

介绍了两种推力销应变桥路，来测量航空发动机推力；根据发动机推力销的实际承力形式，推导出推力销载荷分布公式；利用ANSYS对推力销有限元模型进行了载荷仿真，并分析了推力销所承受的推力与应变之间的关系。通过对剪力应变桥和弯矩应变桥对比分析发现，剪力桥和弯矩桥都与推力呈线性关系；从应变数值大小来看两种桥路均具有工程实用性，但从误差分析来看弯矩桥更具操作性。这些结论为后期开展推力销载荷标定试验提供了理论参考。

航空发动机；推力销；矢量推力；应变 ；ANSYS

Abstract: Two kinds of strain bridge to build mathematical equations are introduced between thrust and strain in aero-engine thrust pin. Based on the actual bearing strength form of thrust pin, mechanics equation on the load distribution was deduced. the structure static analysis was simulated by using ANSYS software. The simulation showed whichever bending area or shear area the relation between thrust and strain were linear well. Strain calculations value in bending strain area and in shear strain area are very close, and so two strain bridges above are both practical in engineering. But from error analysis the bend strain bridge was much smaller and more operational than the other. These conclusions provided theoretical reference in carrying out load calibration tests in thrust pin.

Key words: aero-engine; thrust pin; vector thrust; strain; ANSYS

0 引 言

推力矢量技术是第四代先进战斗机的标志性技术之一，是指飞机的动力装置配装推力矢量喷管后，发动机除了为飞机提供前进方向的推力外，还能同时或单独在飞机的俯仰、偏航、横滚和反推力等方向上提供推力分量，用以补偿或取代由飞机舵面产生的外部气动力，从而提高飞机的飞行控制能力。推力矢量技术的实施，赋予飞机以过失速超机动性、高敏捷性、短距起降性能、低可探测性和超音速巡航能力，大大提高了战斗机的作战效能和生存能力[1-2]。

飞机的动力装置配装推力矢量喷管后，要实现发动机矢量推力和飞机气动舵面的协同操纵，使飞机的升降舵、方向舵、襟翼、副翼和发动机喷管等操纵部件的运动达到最佳化，气动舵面与推力矢量的综合控制技术就成为现代飞行控制系统设计的关键技术之一。在装有矢量喷管的飞机飞行控制系统设计中，需要计算推力和推力矢量的值，因此要求直接测量发动机的矢量推力。20世纪90年代，NASA为了研究推力矢量与飞机的综合控制技术，在F-15ACTIVE项目中开展了发动机推力直接测量技术的研究和飞行试验[3]。推力直接测量技术的原理就是将发动机的推力销进行应变计改装，使其成为一个高精度的力传感器，感受发动机传递给飞机的载荷，从而达到发动机推力直接测量的目的。影响试验精度和误差的关键技术就是推力销的载荷标定试验技术，获得推力校准方程。

为了获得高精度的推力校准方程，就需要对航空发动机进行载荷仿真，开展应力应变分析，为载荷标定试验提供理论指导。

1 推力销受力分析

发动机通过安装节安装在飞机短舱内，并通过推力销将推力传递给飞机。如图1所示，当发动机的推力作用于短而粗的推力销时，在应力及变形分析过程中剪切应力与弯曲应力数值相近，不能简化为常用的欧拉梁，而应该简化为既包括弯曲应力又考虑剪切应力的铁木辛哥(Timoshenko)梁。根据工程经验，将二向垂直应变花贴在贴片截面3和4位置，且应变花与OZ轴呈45°夹角时，可以测到最大切应变数值；将单向应变片贴在贴片截面1和2位置，可获得最大弯曲正应变[4]。

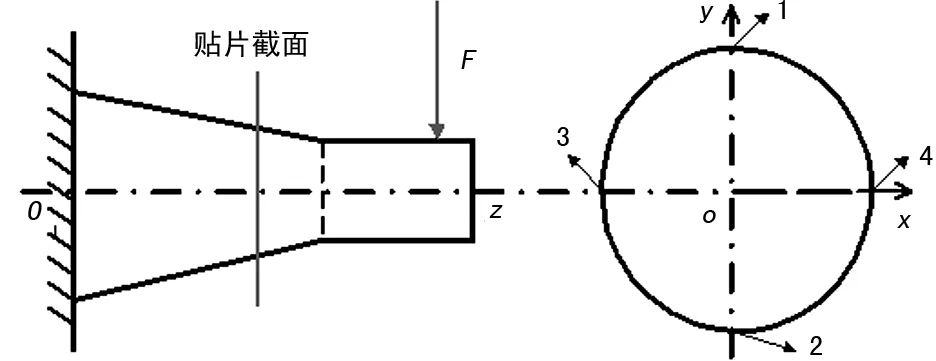
图1 推力销受力及贴片区示意图

由于推力销所处的环境恶劣，温度变化大，为了消除温度对其影响，提高测量精度，需要将对称面1和2的应变计组成半桥，而对称面3和4的应变花则要组成全桥。因此在推力销标定试验之前需要研究弯曲应变和切应变与力之间的关系，以确定采用何种桥路。

对于圆柱体零件而言，受到径向力作用时，接触面处的载荷呈现余弦分布[5]，如图2所示。

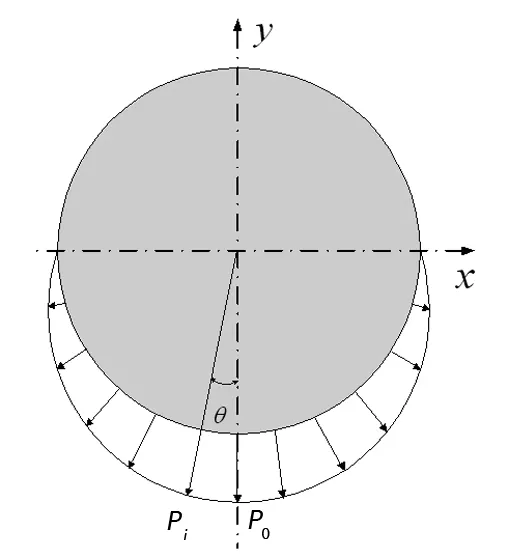
图2 圆柱面径向受力载荷分布图

发动机推力传递到推力销时可近似为静载荷，推力销受力面厚度z轴方向为恒值，推力载荷沿x-y平面呈余弦分布，载荷方向由圆心指向载荷微面处，即Pi=P0cosθ，其中在推力销受力方向存在最大的面载荷P0。Pi沿x轴方向的载荷分量会抵消为零，剩下y轴方向载荷，以Pi为例易得出：

Piy=Picosθ

(1)

将式(1)沿x方向进行积分有：

(2)

式中：t为z轴方向厚度，r为受力面圆弧半径，Fr为推力值，将x2+y2=r2带入式(2)，在极坐标下求解积分方程有：

(3)

将式(3)代入Pi=P0cosθ，则推力销径向载荷的分布式为:

(4)

2 推力销有限元建模

在有限元软件里，进行网格划分时倒角倒圆等小特征会产生大量的小网格，甚至造成无法对实体进行网格划分，而大量实践证明，忽略小特征几乎不会影响分析结果[6]。因此该研究模型没有生成倒角倒圆，将UG实体模型导入到ANSYS中，利用精度高的SOLID95六面体单元对推力销进行网格划分，并对受力区域和贴片区域进行网格细化，得到16421个单元，30214个节点。

假定模型所承受的y方向推力为104N，笔者利用柱面坐标系施加载荷，则载荷函数为2.078×107cosθ(Pa),其中θ为载荷与y轴方向之间的夹角，利用“载荷函数编辑器”实现载荷加载[5]，最终加载的面载荷如图3中有限元模型中箭头所示。

图3 推力销有限元模型

根据推力销的实际固定形式，对推力销固定面处的6个螺栓孔附近节点施加X、Y、Z方向的位移全约束；在接触面其他区域只对X方向进行位移约束，以实现与实际约束一致[5-7]。

图4为推力销等效应变云图，可以看出接合面处存在应力集中，除了结合面外，应变在受力端和锥形面上分布复杂，需进一步针对贴片区域各个方向的正应变和切应变进行数值分析。

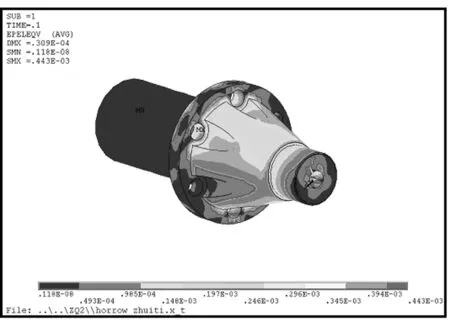
图4 推力销等效应变云图

3 推力销有限元分析

3.1 弯矩桥和剪力桥应变分析

为了探究贴片位置处正应变和切应变的数值关系，选取圆锥面中性层(图1中3、4位置)附近的区域，区域大小以应变花大小为标准，分别简称为测剪区一和测剪区二；以及圆锥面远离中性层 (图1中1、 2位置) 附近区域，分别简称为测弯区一和测弯区二。由于应变片只能测量平面应力，在测剪区只需对比正应变εy、εz以及切应变γyz，在测弯区需对比正应变εx、εz以及切应变γxz。根据应变片所测区域，统计该区域内的节点应变数值的平均值，如表1。

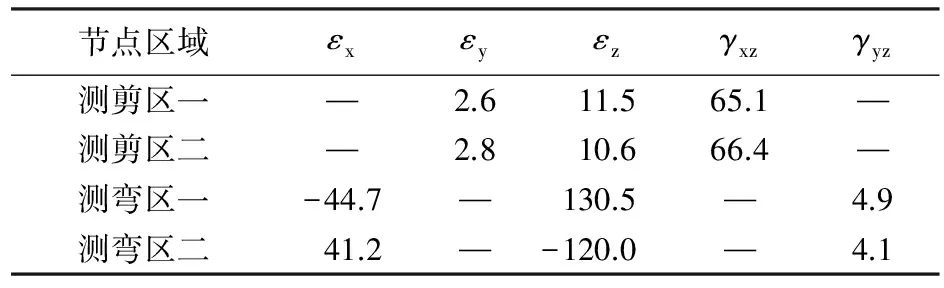
表1 推力销应变统计表 /με

从表1可看出，测剪区切应变为65 με，组成全桥后切应变为4γxz，电桥输出的应变值为260 με；测弯矩区主应变Z方向的线应变为120 με，组成半桥后线应变为2 ε，电桥输出的应变值为250 με。可以看出剪力桥和弯矩桥的测量数值大小是相当接近的，在理论上讲测剪桥路和测弯桥路都是可行的。

在工程贴片过程中，难免会出现贴片位置和角度出现偏差的情况，还需结合实际情况分析两种桥路的工程误差。根据应变摩尔圆公式可知，贴片方向与主应变角度为β时，贴片位置的线应变为[8]：

(5)

当实际贴片位置偏离设计角度Δβ时，得到读数误差式(6)，并利用泰勒展开式，忽略高阶项，有：

Δεβ=εβ+Δβ-εβ

(6)

假设贴片误差角为3°，根据式(6)，对于测剪桥路β近似为45°，相对误差为5%；对于测弯桥路β近似为0°，相对误差为0.25%，可以看出测弯桥路误差几乎可以省略。

3.2 推力与应变的变化规律

通过在ANSYS软件施加不同推力所对应的载荷

函数，并重复进行推力销静力分析，统计测剪区的切应变和测弯区的正应变，得到了图5不同推力值与应变的变化关系，从图5可看出四个区域里的应变与推力之间呈良好的线性关系。

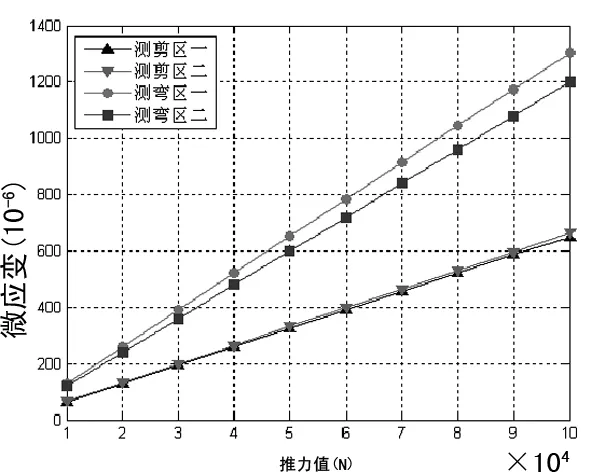
图5 不同推力与应变变化曲线

4 结 论

(1) 根据推力销实际承力形式，推导出了推力销载荷分布式：

(2) 利用ANSYS对比分析了推力销测剪应变和测弯曲应变的应变数值关系，理论上讲测剪和测弯桥路都具有工程实用价值，但从工程误差分析，测弯桥路误差很小，更具有工程操作性。

(3) 对于推力销测剪力应变和测弯矩应变桥路而言，推力与应变都呈线性关系。

[1] 陶增元,李 军,程邦勤. 飞机推进系统关键技术——推力矢量技术[J]. 空军工程大学学报(自然科学版)，2000,1(2):86-90.

[2] 王红艳,孙宝元.基于有限元分析的推力矢量测量平台研究[J].压电与声光，2006,28(5):618-620.

[3] Timothy R，Coner and Robert L.Sims. Full Flight Envelop Direct Thrust Measurement on a Supersonic Aircraft[R]. American Institute of Aeronautics and Astronautics, NASA/TM-1998-206560: California NASA,1998,July:1-36.

[4] 吴宗岱,陶定祺.应变电测原理及技术[M].北京：国防工业出版社,1982.

[5] 雷晓波.基于实验和ANSYS的转子支座静刚度分析研究[D].西安：西北工业大学,2013.

[6] 仪登利,曾 红,王新丰.铝合金轮毂UG建模ANSYS分析时的模型导入问题[J]. 辽宁工业大学学报,2008,28(1): 36-38.

[7] 杜洪奎.螺栓联接结构的有限元模拟计算[J].压缩机技术, 2004(2):11-13.

[8] 杨 琳.应变测量方位设计及方位偏差修正方法探讨[J].飞行试验,2010,26(2):23-25.

Load Calculation and Strain Analysis for Aero-Engine Thrust Pin

LEI Xiao-bo, ZHANG Qiang, ZHANG Yong-feng

(ChineseFlightTestEstablishment，Xi′anShaanxi710089,China; )

2014-06-19

中航工业创新基金基础类项目(编号：2012A63033R)航空发动机矢量推力直接测量技术。

雷晓波(1986-)，男，陕西合阳人，助理工程师，硕士，研究方向:发动机结构强度飞行试验技术研究、旋转机械故障诊断。

V232.2

A

1007-4414(2014)04-0032-03