n值逻辑系统中条件随机真度理论

2014-07-24黎丽

纯粹数学与应用数学 2014年6期

关键词：概率分布度量命题

黎丽

n值逻辑系统中条件随机真度理论

黎丽

(桂林航天工业学院理学部,广西桂林541004)

在n值命题逻辑系统中命题的随机真度、随机逻辑度量空间的基础上,给出了修正的n值G¨odel命题逻辑系统中命题的条件真度、条件相似度的概念并讨论了其性质,建立了条件随机逻辑度量空间.

随机真度;条件真度;条件相似度;条件逻辑度量空间

1 引言

在计量逻辑学中,从把逻辑概念程度化入手,给出了公式的真度概念,建立了计量逻辑学理论[1-4].由于计量逻辑学中,每个原子公式的真度都相等,这就使得如果两个公式完全一致,那么它们的真度也一定相等.这种把每个原子公式的真度等同看待的观点,显然与客观世界中各原子公式的概率不尽相同的事实相违背,所以赋予不同原子公式以不同的概率,可以使命题公式的真度更接近现实世界.基于这样的考虑,文献[5-7]就二值和三值逻辑系统提出了随机真度的概念,文献[8]在n值逻辑系统中引入了随机真度的概念,研究相似度和伪距离,建立了随机逻辑度量空间.把概率逻辑学[9]中条件概率部分通过恰当的途径与真度相结合,并能使其指导生活实践,这是一个十分有意义的课题.

继n值命题逻辑系统中命题随机真度的研究成果,本文在修正的n值G¨odel命题逻辑系统中引入了命题的条件随机真度、条件随机相似度和条件随机伪距离的概念并研究了其性质,从而建立了条件随机度量空间.因此可以把n值逻辑系统中计量逻辑学的程度化研究以及近似推理模式等纳入到本文给出的更为宽泛的研究体系之中.

2 n值随机逻辑度量空间

定义2.1[2]设S={q1,q2,···}是可数集,称为原子公式集,“⇁”是一元运算,“∨”与“→”是二元运算,F(S)是由S生成的(⇁,∨,→)型自由代数,称F(S)中的元素为公式或命题,S中的元素叫原子公式或命题变元.

在本文中,记

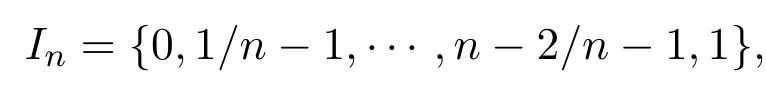
其中n为大于等于2的正整数.

在In={0,1/n−1,···,n−2/n−1,1}中,运算“⇁”,“∨”与“→”分别定义为:

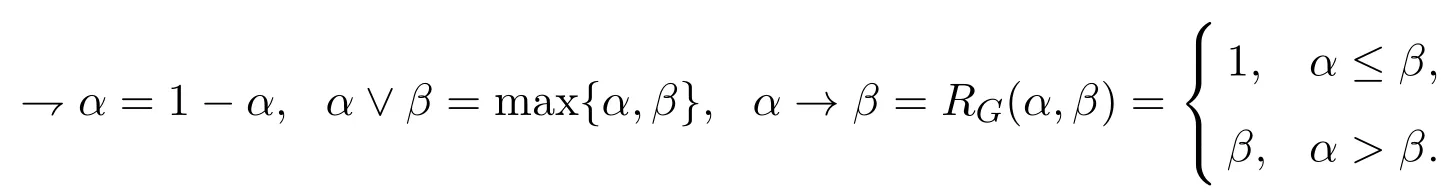
则In成为(⇁,∨,→)型代数,称为修正的n值G¨odel逻辑系统,记作Gn.

本文在修正的n值G¨odel逻辑系统Gn中展开讨论.

定义2.2[4]设ν:F(S)→Gn是映射,若ν满足:

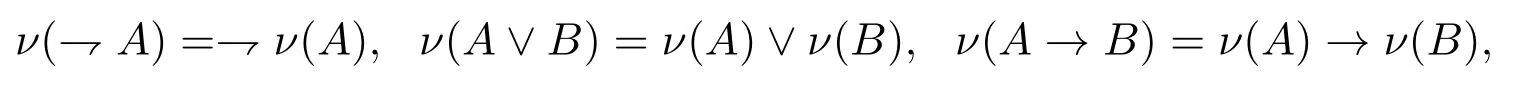
则称ν是F(S)在Gn中的一个赋值,称作公式A的赋值.F(S)的赋值映射的全体记为Σ(Gn), Gn称为赋值域.

设A=A(q1,···,qm)是含有m个原子公式q1,···,qm(为了与概率分布中的符号p相区别,本文用q来表示原子公式)的命题公式,设Gn是赋值域,分别用Gn中的x1,···,xm去取代q1,···,qm,并且把A中的逻辑联结词“⇁”,“∨”,“→”分别换成Gn中的运算“⇁”,“∨”,“→”,则得到m元函数:

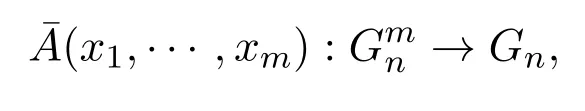
定义2.3[8]设N={1,2,···},ξ=(ξ1,ξ2,···),其中

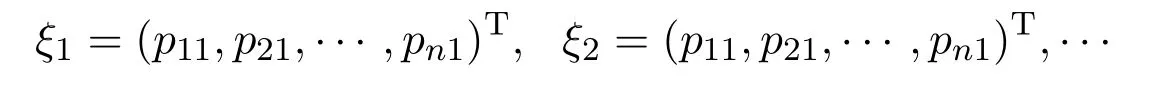
称ξ=(ξ1,ξ2,···)为随机概率分布序列(ξ是一个n行可数列矩阵).

注2.1(i)要求概率分布中的每一个元素pij均大于0;

(ii)概率分布ξ1,ξ2,···是各自独立的;

(iii)随机概率分布序列ξ构成的矩阵的每一列元素之和等于1,但不要求每行元素之和等于1.

定义2.4[8]设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,其中

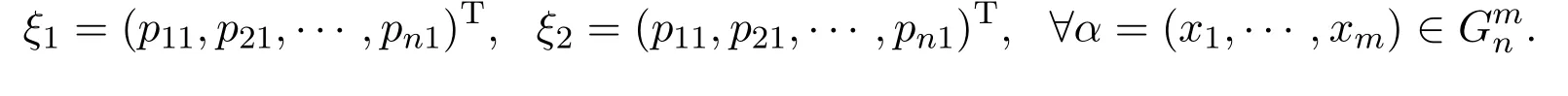
令φ(α)=Q1×Q2×···×Qm.当时,则

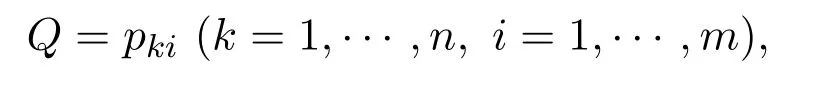
命题2.1∑{φ(α):α=(x1,···,Xm)∈}=1,即φ()=1.

证明对m用数学归纳法,当m=1时,

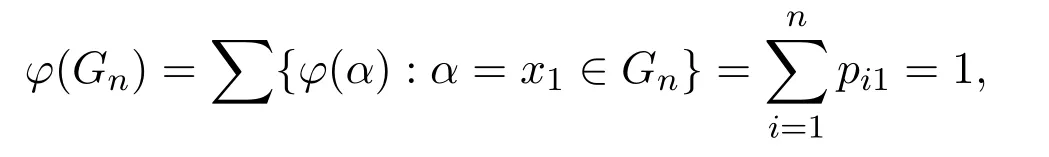
用数学归纳法易证:

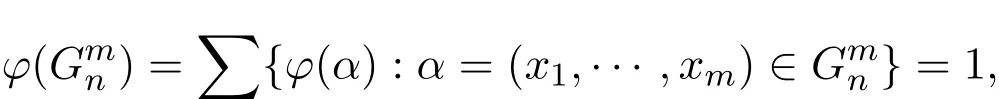
定义2.5[8]设

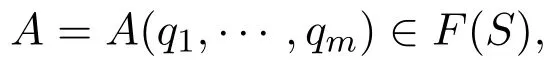
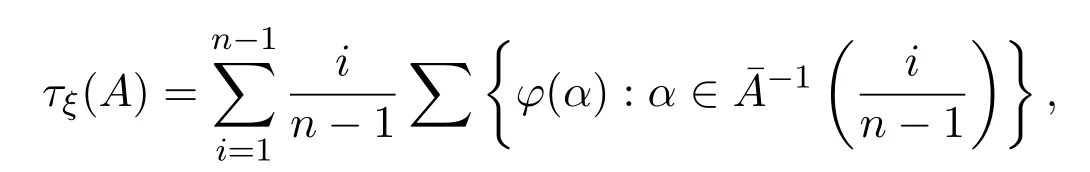
则称τξ(A)为公式A在修正的n值G¨odel逻辑系统Gn中基于随机概率分布序列ξ的随机真度,简称为公式A的ξ-随机真度.

定理2.1[8]设A,B∈F(S),ξ=(ξ1,ξ2,···)为一个随机概率分布序列,则以下各结论成立:

(i)A是重言式当且仅当τξ(A)=1,A是矛盾式当且仅当τξ(A)=0;

(ii)若A≈B,则τξ(A)=τξ(B);

(ii)τξ(⇁A)=1−τξ(A);

(iv)τξ(A∨B)=τξ(A)+τξ(B)−τξ(A∧B).

定义2.6[8]设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,A,B∈F(S).令

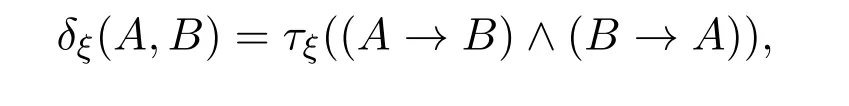
称δξ(A,B)为公式A与B的ξ-随机相似度.显然有δξ(A,B)=δξ(B,A).

设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,A,B∈F(S),令ρξ(A,B)=1−δξ(A,B),则ρξ为F(S)上的伪距离,称为ξ-随机伪距离,称(F(S),ρξ)为ξ-随机逻辑度量空间.

下面在修正的n值G¨odel逻辑系统Gn中引入条件随机真度、条件随机相似度和条件随机伪距离的概念,研究其性质,建立条件随机逻辑度量空间.

3 条件随机真度

定义3.1设A=A(q1,···,qm)∈F(S),ξ=(ξ1,ξ2,···)为一个随机概率分布序列,Λ∈F(S)且τξ(Λ)>0,令τξ(A|Λ)=,则称τξ(A|Λ)为公式A在条件Λ下的ξ-条件随机真度.

定义3.2设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,A,B∈F(S),Λ∈F(S),且τξ(Λ)>0.

定理3.1设ξ=(ξ1,ξ2,L)为一个随机概率分布序列,A∈F(S),Λ∈F(S),且τξ(Λ)>0,则

(i)若A=Λ1,则τξ(A|Λ)=1;

(ii)若A=Λ0,则τξ(A|Λ)=0;

(iii)若A≈ΛB,则τξ(A|Λ)=τξ(B|Λ);

(iv)τξ(A∧B|Λ)=τξ(A|Λ)+τξ(B|Λ)−τξ(A∧B|Λ).

证明(i)不妨设A和H含有相同的原子公式q1,···,qm.

由运算的同态性,可得

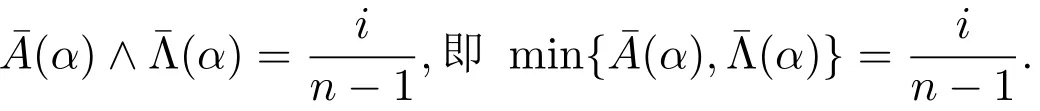
由A=Λ1知,

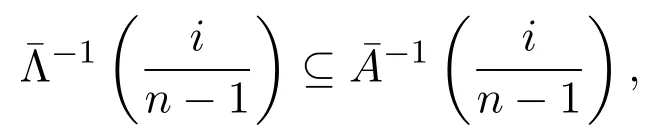
所以由

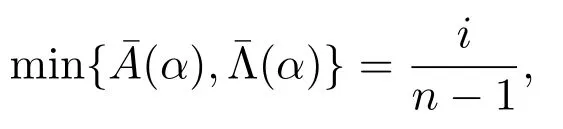
得

由于

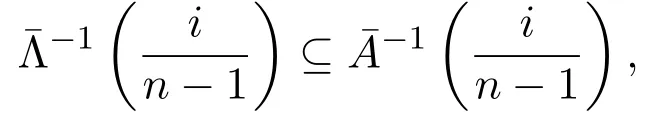
则可得,

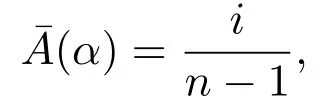
于是

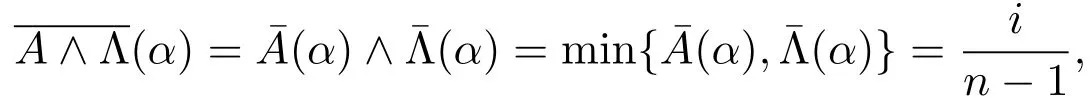
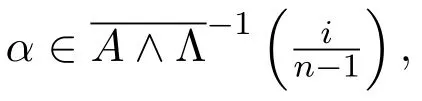
即至此证明了

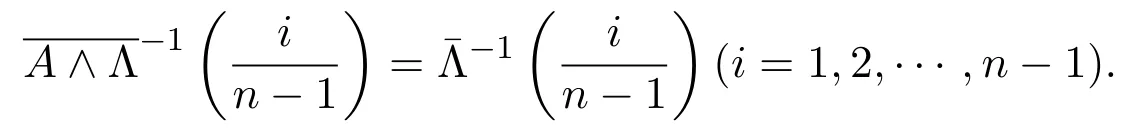
于是得:

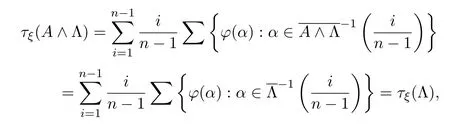
故得

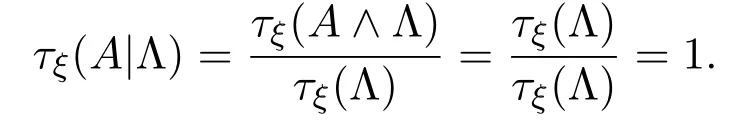
(ii)因为

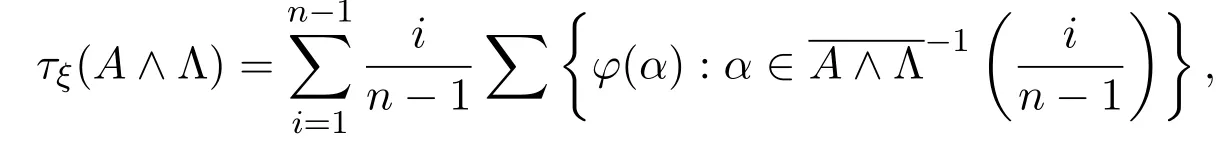
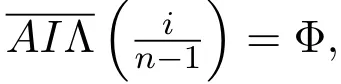
由故显然得τξ(A∧Λ)=0,于是τξ(A|Λ)=0.

(iii)因为A≈ΛB,则由定义2.2知,当i=1,2,···,n−1时,均有

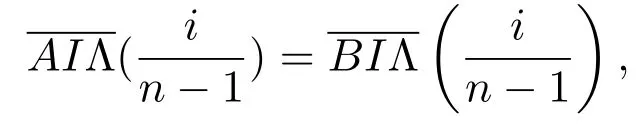
故

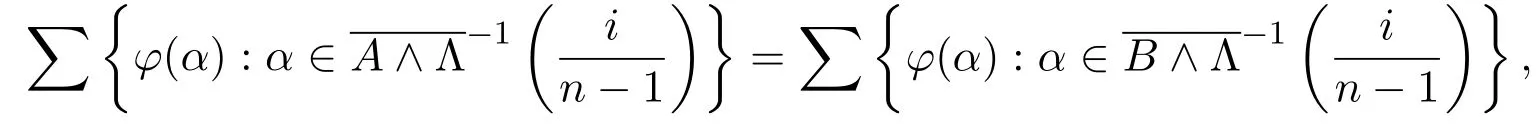
于是,

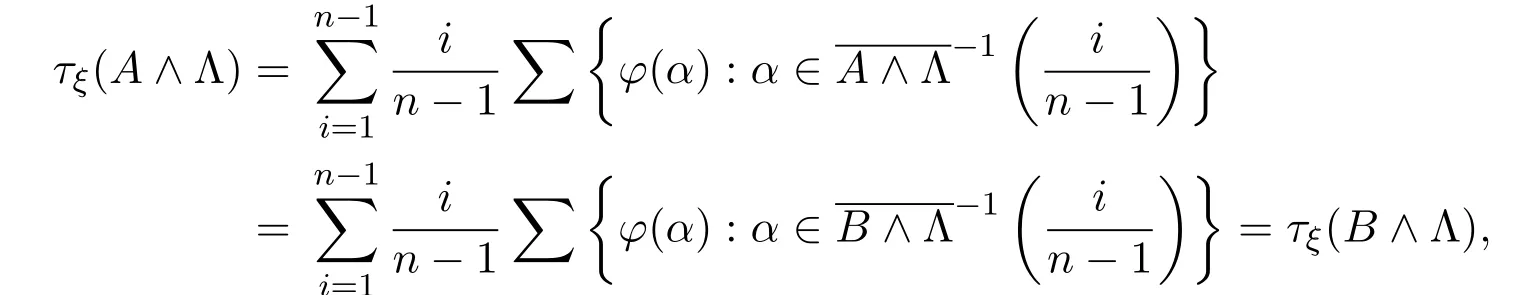
故得τξ(A|Λ)=τξ(B|Λ).

(iv)由定理2.1得,

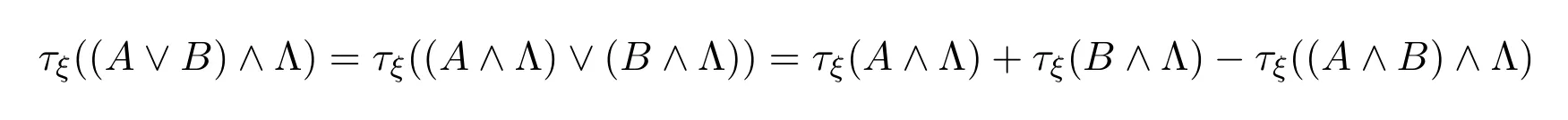
上式两边同时除以τξ(Λ)即得结论.

4 条件随机逻辑度量空间

定义4.1设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,A∈F(S),Λ∈F(S),且τξ(Λ)>0,令δξ(A,B|Λ)=τξ((A→B)∧(B→A|Λ)),则称δξ(A,B|Λ)为公式A与B在条件Λ下的相似度.

定理4.1设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,Λ∈F(S),A,B,C∈F(S),且τξ(Λ)>0.则

(i)若A≈ΛB,则δξ(A,B|Λ)=1;

(ii)δ(A,B|Λ)+δ(B,C|Λ)≤1+δ(A,C|Λ).

证明(i)因为A≈ΛB,则A→B和B→A,都是基于Λ的重言式,则(A→B)∧(B→A)也是基于Λ的重言式,则由定理3.1得,

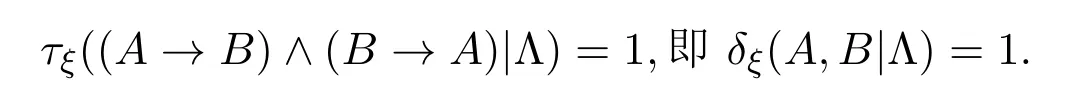
(ii)为了证明结论成立,先给出ξ-随机真度公式的一个变形,即

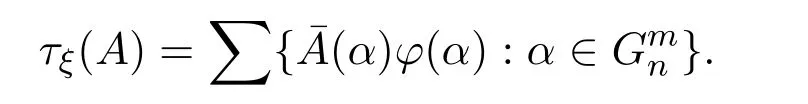
事实上,

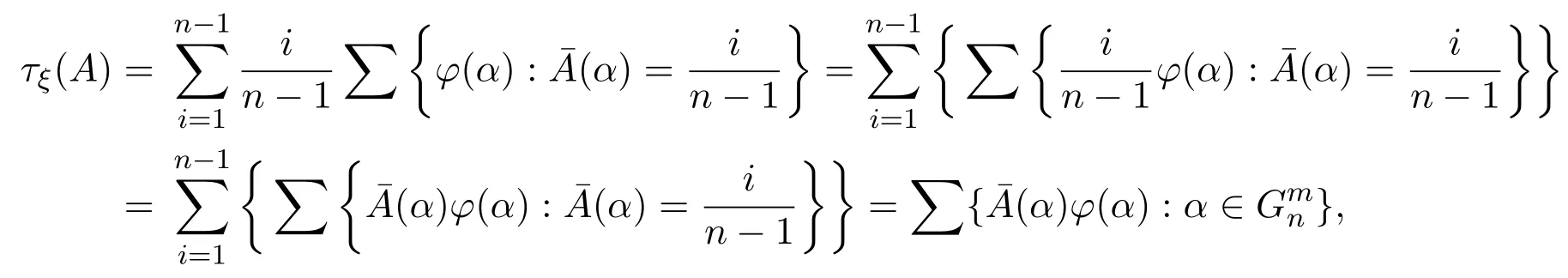
即结论成立.

另一方面,设a,b,c∈Gn,则对于修正的n值G¨odel逻辑系统Gn的蕴涵算子,可以验证(a→b)∧(b→a)+(b→c)∧(c→b)−(a→c)∧(c→a)≤1成立.

又因为¯A(x1,···,xm):Gmn→Gn,是Gmn到Gn的同态映射,于是有,

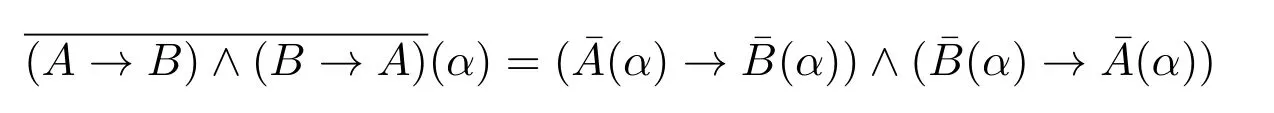
于是

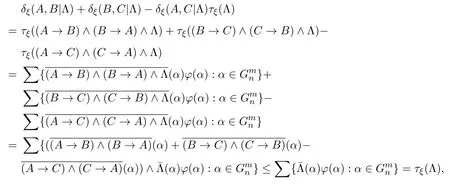
于是就得到,δξ(A,B|Λ)+δξ(B,C|Λ)−δξ(A,C|Λ)≤1,结论成立.

又因为ρξ(A,A|Λ)=0和ρξ(A,B|Λ)=ρξ(B,A|Λ)显然成立,所以ρξ为F(S)上的条件伪距离.称为在条件Λ下的条件随机伪距离.

定义4.2设ξ=(ξ1,ξ2,···)为一个随机概率分布序列,Λ∈F(S),A,B,C∈F(S),且τξ(Λ)>0,则ρξ为F(S)上的条件伪距离,称(F(S),ρξ)为条件随机逻辑度量空间.

由此定义3.2和定理3.1显然得:

定理4.2设ξ=(ξ1,ξ2,···)为随机概率分布序列,Λ∈F(S),且τξ(Λ)>0,A,B∈F(S),若A≈ΛB,则ρξ(A,B|Λ)=0.

5 结束语

本文在修正的n值G¨odel命题逻辑系统中引入了命题的条件随机真度、条件随机相似度和条件随机伪距离的概念,研究了其性质,从而建立了条件随机度量空间.如何进一步在n值命题逻辑系统的条件随机度量空间中展开近似推理以及拓扑性质的研究,将另文讨论.

[1]Wang G J,Leung Y.Integrated semantics and logic metric spaces[J].Fuzzy Sets and Systems,2003,136(1):71-91.

[2]王国俊,李璧镜.Ukasiewicz值命题逻辑中公式的真度理论和极限定理[J].中国科学:E辑,2005,35(6):561-569.

[3]王国俊,王伟．逻辑度量空间[J]．数学学报,2001,44(1):159-168.

[4]王国俊.计量逻辑学(I)[J].工程数学学报,2006,23(2):191-215.

[5]惠小静,王国俊．经典推理模式的随机化研究及其应用[J]．中国科学:E辑,2007,37(6):801-812.

[6]惠小静,王国俊．经典推理模式的随机化研究及其应用(II)[J]．模糊系统与数学,2008,22(3):21-26.

[7]惠小静.三值命题逻辑系统的随机化[J]．应用数学学报,2009,32(1):19-27.

[8]李修清,魏海新,林亮.修正的n值G¨odel逻辑系统的随机化[J]．计算机工程与应用,2012,48(24):45-49.

[9]Adams E W.A Primer of Probability Logic[M].Stanford:CSLI Publications,1998.

Theory of conditional randomized truth degree in valued logical system

Li li
(Faculty of Science,Guilin University of Aerospace Technology,Guilin541004,China)

Based on randomized truth degrees and randomized logic metric space of n-valued logical system, the concept of conditional truth degree and conditional similarity degree in G¨odel n-valued logical system and their properties are given.The concept of conditional randomized logic metric space is also introduced.

randomized truth degree,conditional truth degree,conditional similarity degree, conditional logic metric space

O159

1008-5513(2014)06-0573-08

10.3969/j.issn.1008-5513.2014.06.005

2014-03-21.

广西壮族自治区教育厅科研项目(桂教科研[2011]14号);桂林航天工业学院基金(YJ1301).

黎丽(1974-),讲师,研究方向:模糊数学与动力系统.

2010 MSC:03E72