具有Kelvin-Voigt阻尼的弱耦合系统的能量衰减估计

樊美丽,章春国,谷尚武

具有Kelvin-Voigt阻尼的弱耦合系统的能量衰减估计

樊美丽,章春国,谷尚武

(杭州电子科技大学数学系,浙江杭州310018)

研究具有Kelvin-Voigt阻尼的弱耦合系统.首先在合适的假设条件下,应用线性算子半群理论证明了系统的适定性;进而运用线性算子半群的频域定理证明了具有Kelvin-Voigt阻尼的弱耦合梁―弦系统的能量是一致指数衰减的.

Kelvin-Voigt阻尼;弱耦合系统;线性算子半群;一致指数衰减

1 引言

基于梁、弦、板等系统在空间科学及机器人学中的广泛应用,由智能材料制成的补钉黏贴在或嵌入到基底结构中作为主动或被动的阻尼器,为了获得最优配置(最佳控制)结果,往往需要知道系统能量衰减与系统参数之间的定量关系,实际系统的控制作用往往取决于系统的这一指标.近二十年来,应用的发展和技术要求的不断提高,驱使国内外许多数学和力学工作者研究各种具有不同类型阻尼的Euler-Bernoulli梁、Timoshenko梁、Rayleigh梁以及Petrovsky板等系统(耦合系统)的稳定性.例如:文献[1-2]研究的是非线性阻尼耦合振动的Petrovsky系统,文献[3-6]考虑的是各种具有不同阻尼的弦、梁及波系统的稳定性.本文考虑一类具有Kelvin-Voigt阻尼的弱耦合系统的稳定性.确切地说,研究如下具有Kelvin-Voigt阻尼的弱耦合系统的初边值问题:

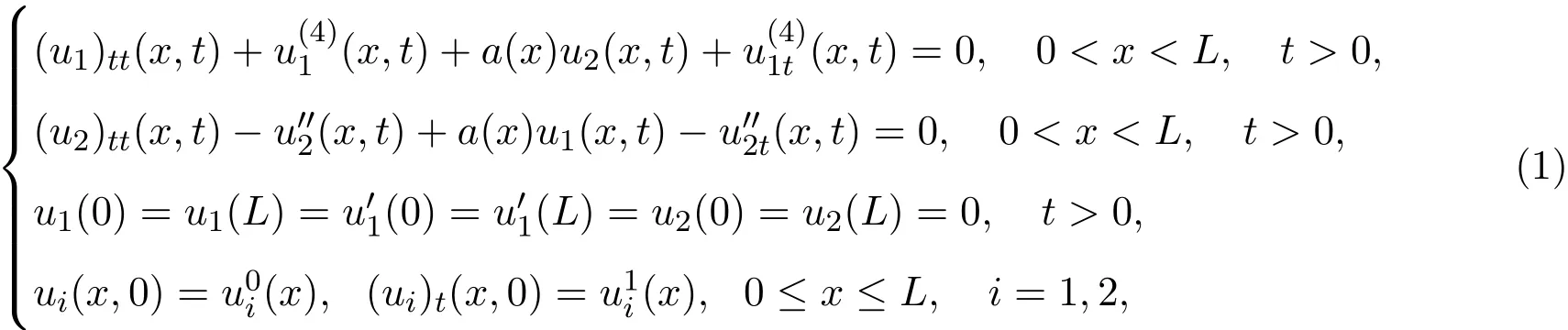
其中“′”表示对空间变量x的导数,a(x)∈L∞(0,L).

本文的方法源于文献[6].在合适的假设下,应用经典结果[7]和C0-半群生成元的预解式在虚轴上的有界性的频域结果[8],并且运用线性算子半群理论、分片乘子技巧以及矛盾的讨论得到了系统(1)的适定性和能量的一致指数衰减性.

2 主要结果

为了研究系统(1)的稳定性,作如下的假设:

(H1)假设

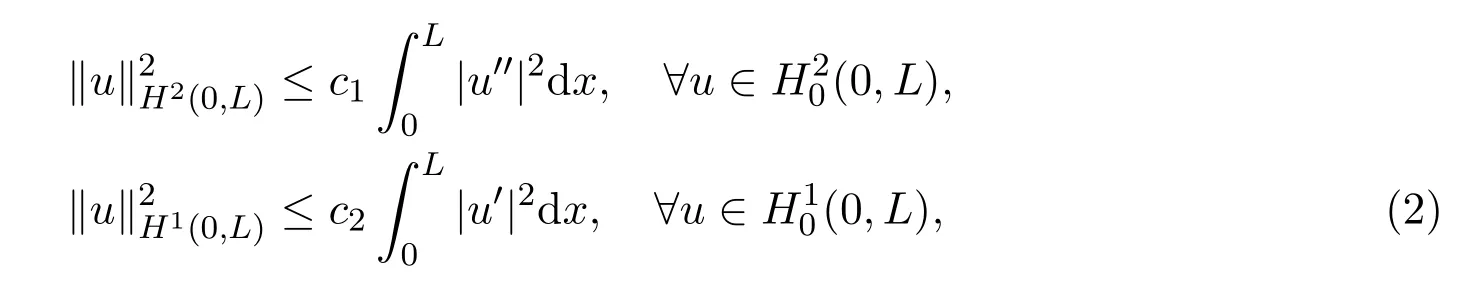
其中Poincare常数c1,c2>0.为了方便起见,记∥a∥L∞(0,L)为∥a∥∞.

(H2)

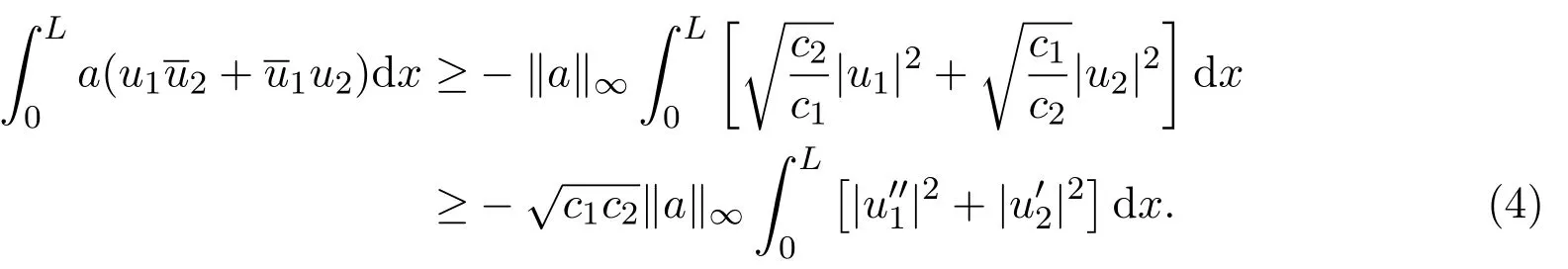
定义系统(1)在时刻t的能量为:

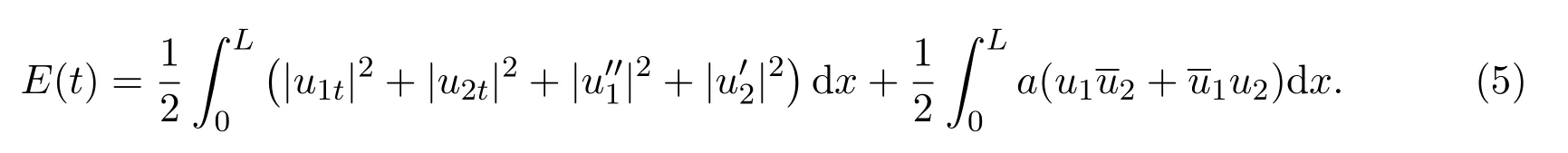
引入Hilbert空间

其中Hk(0,L)是k阶Sobolev空间[9].并赋予范数:

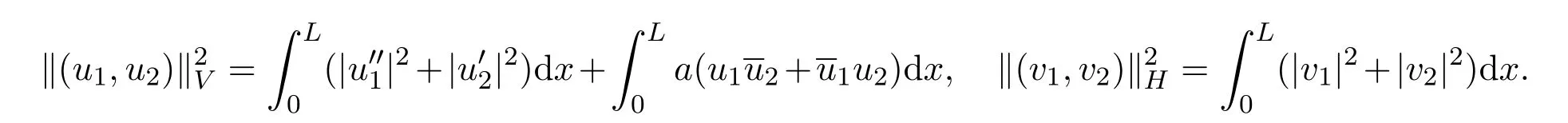
因此V,H均为Hilbert空间.

设

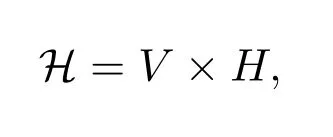
并赋予范数:

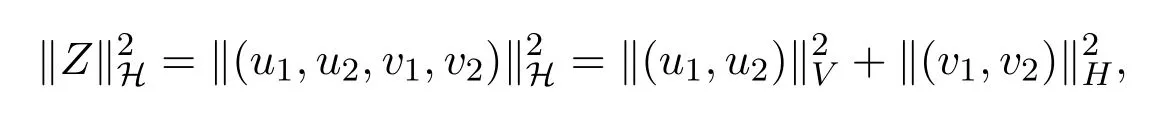
那么H也是Hilbert空间.

在H中定义线性算子A如下:

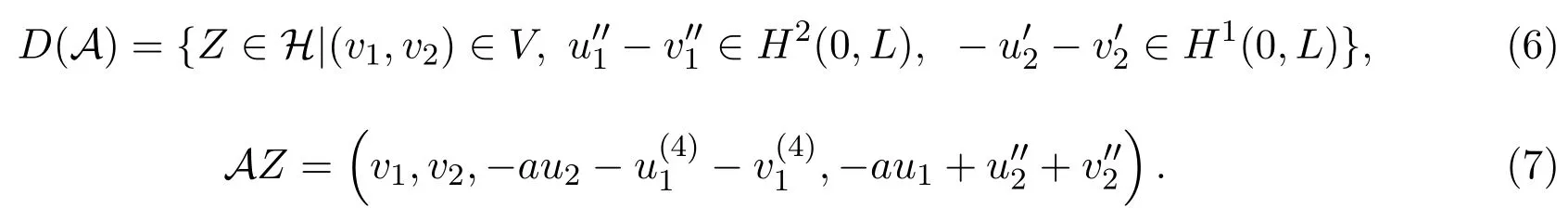
那么,可以将系统(1)改写成H上的抽象Cauchy问题:

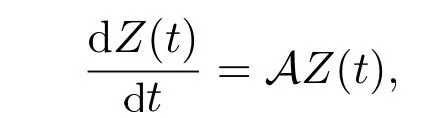
其中Z=(u1,u2,v1,v2),

现在叙述本文的主要结果:

定理2.1如果假设(H1)-(H2)成立,那么A是H上压缩C0-半群eAt的无穷生成元.进一步,若(u01,u02,v01,v02)∈D(A),则系统(1)存在唯一的强解;若(u01,u02,v01,v02)∈H,则系统(1)存在唯一的弱解.

定理2.2如果假设(H1)-(H2)成立,那么系统(1)的能量是一致指数衰减的.

3 系统的适定性和半群的谱性质

首先证明算子A生成H上的压缩C0-半群eAt,进而证明系统的适定性,并且得到线性算子A的谱性质.

定理2.1的证明对于任意的Z=(u1,u2,v1,v2)∈D(A).由分部积分得,

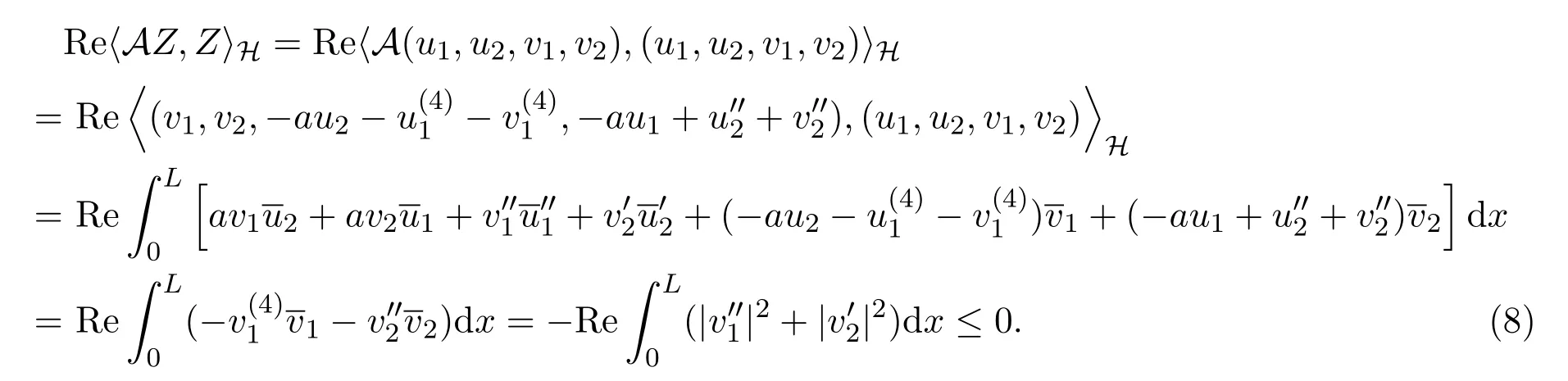
因此A在H中是耗散的.易知kerA={0},对∀Z1=(f1,f2,f3,f4)∈H,求解方程:

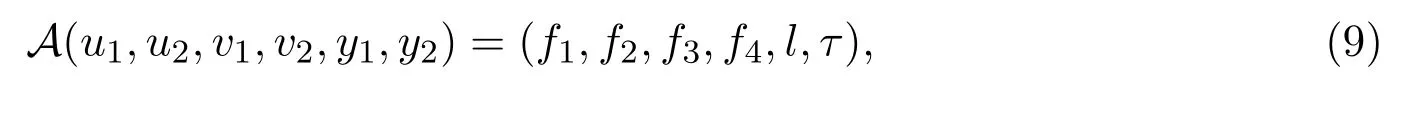
即

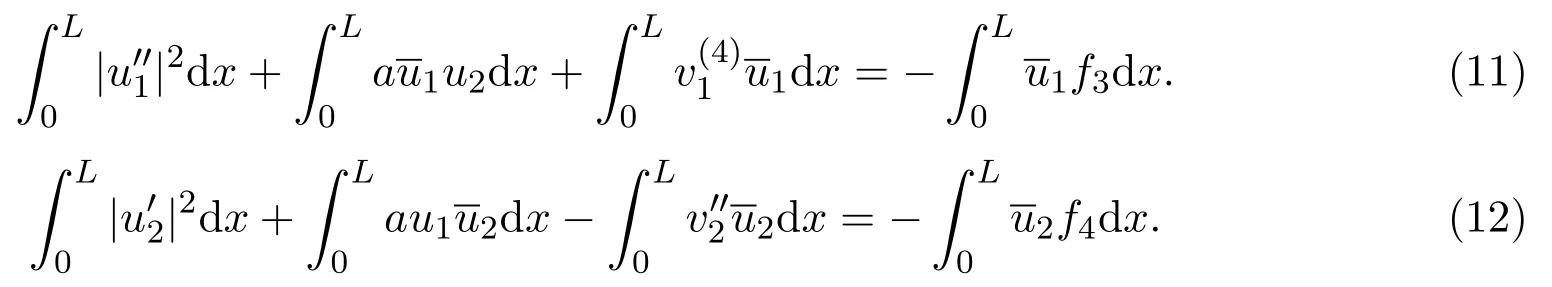
将(11)和(12)两式相加,分部积分,并应用边界条件得:

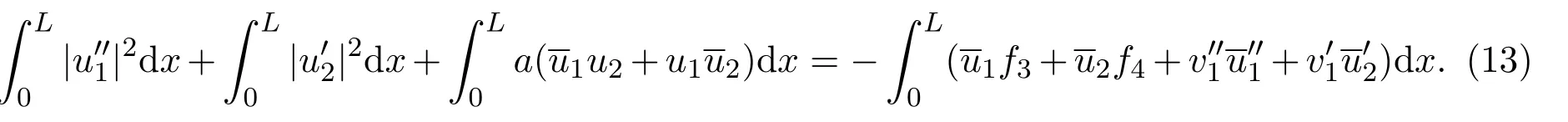
于是由(13)式,(H1)和带权Cauchy不等式得:

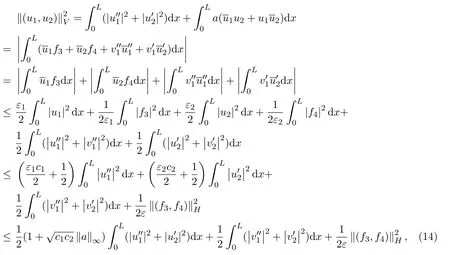
另一方面,由(4)式得,

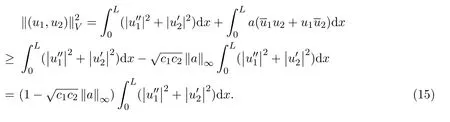
于是由(14)和(15)两式得:

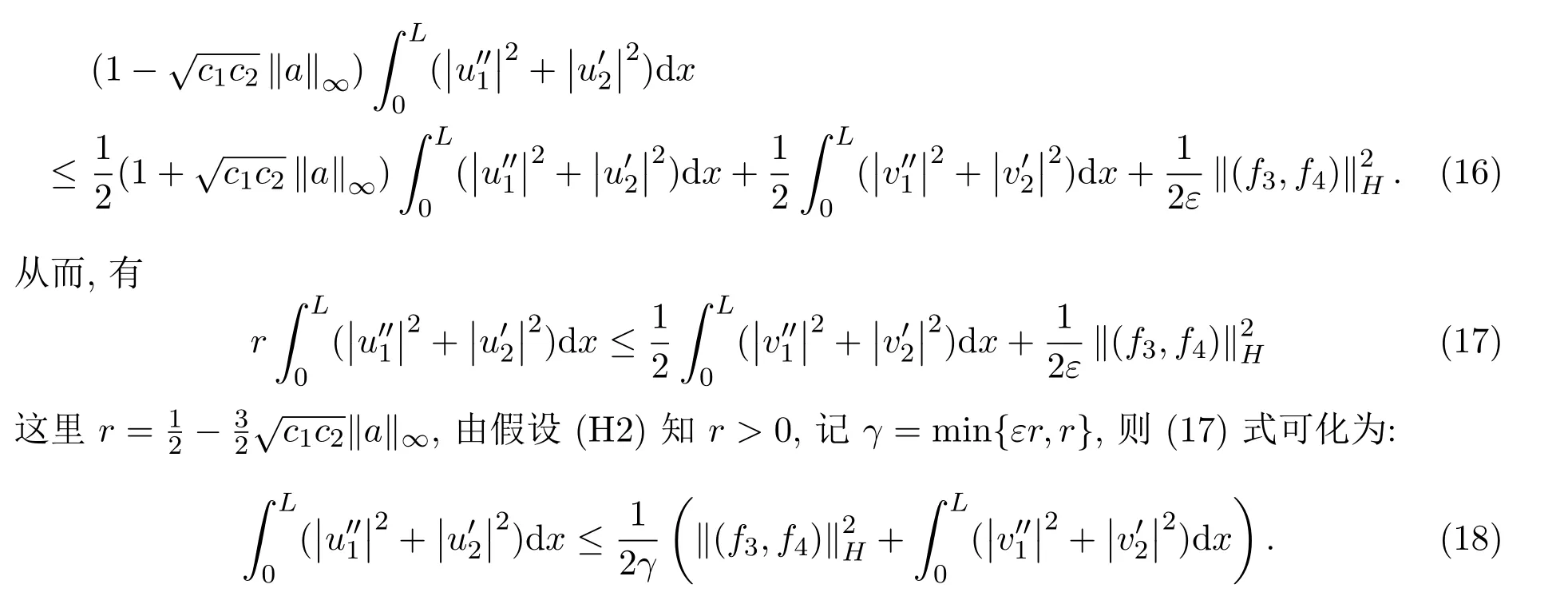
于是存在正数M1,使得

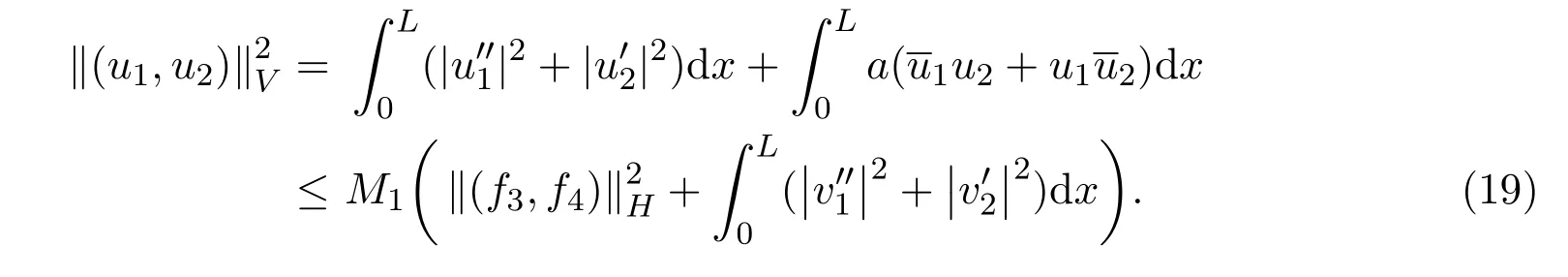
由(10)式和假设(H1),(H2)得:存在正常数C1,C2,使得

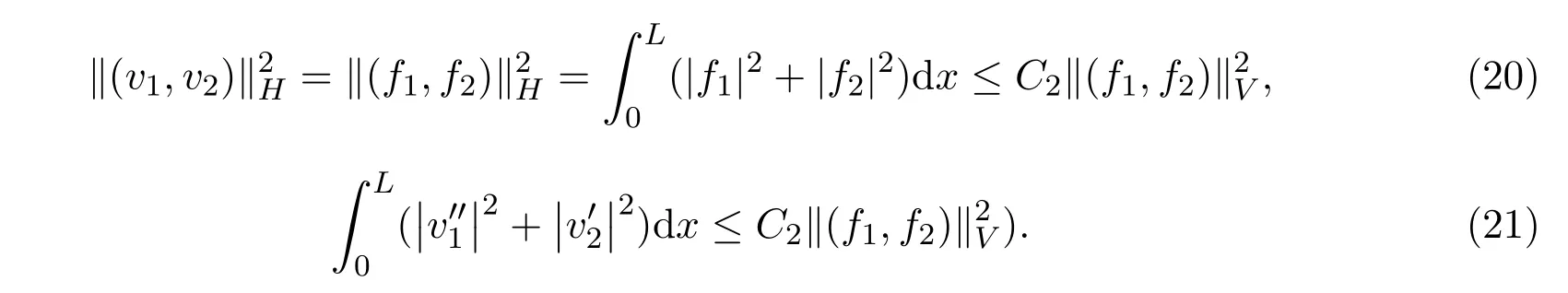
由(19)-(21)式得到:存在某个常数M>0,使得∥Z∥H≤M∥Z1∥H.因此,

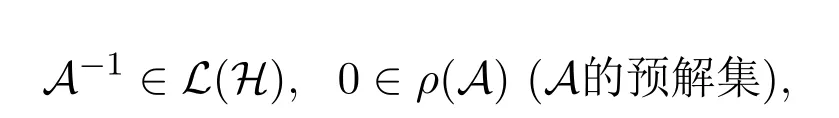
且A是闭的.对足够小的λ>0,λI−A的值域rg(λI−A)=H,故由文献[7]定理1.4.6知则应用Lumer-Phillips定理即证明了A是H上压缩C0-半群eAt的无穷生成元.

进一步,若(u01,u02,v01,v02)∈D(A),则系统(1)存在唯一的强解:

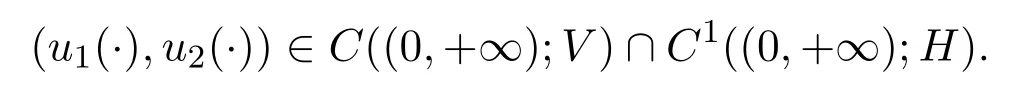
性质3.1iR⊂ρ(A).

证明首先,证明A具有紧的预解式.

不妨设{Yn|n≥1}⊂H是一有界序列:对于n≥1,≤C成立.由上面的证明可得λ=0∈ρ(A).则令Zn=A−1Yn,有∥AZn∥H≤C,根据Sobolev嵌入定理可知,在Zn中能够找到收敛的子列,因此A−1是紧的.

由引理4.1[10]的类似证法,可得:

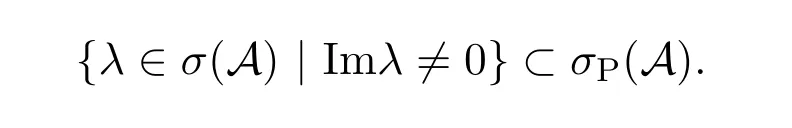
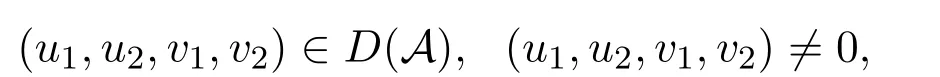
使得

则由(8)式可得,

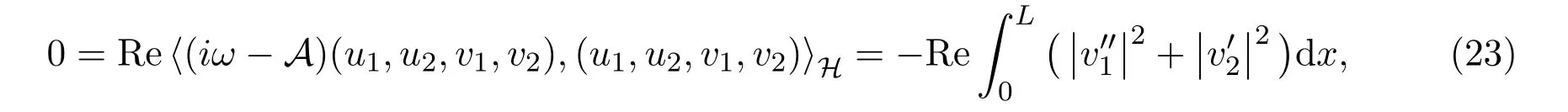
因此在L2(0,L)中有注意到,

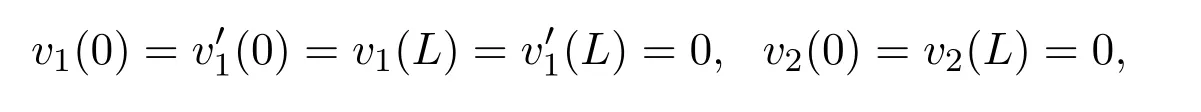
那么在(0,L)中,有

由(22)式以及算子A的定义得到:

故在(0,L)上,有(u1,u2,v1,v2)=0与假设矛盾.因此原命题成立.

4 定理2.2的证明

若u1(x,t),u2(x,t)是系统(1)的解.那么有:

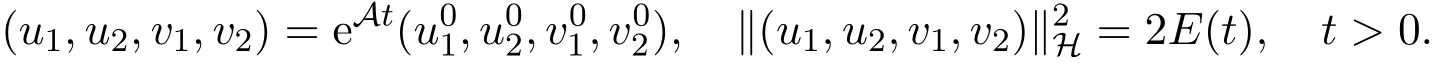
能量E(t)的一致指数衰减性等价于C0-半群eAt的一致指数稳定性.由性质3.1和频域结果[8],只需证明:

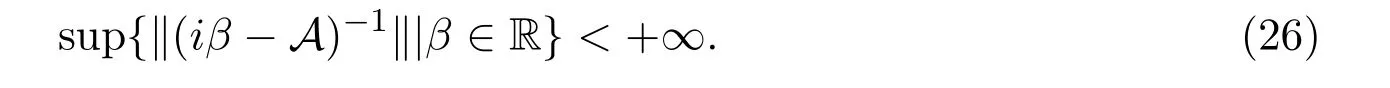
假设(26)式不成立,即sup{∥(iβ−A)−1∥|β∈R}=+∞,由一致有界性定理和预解式的连续性知,存在{βn}⊂R和{Zn=(u1n,u2n,v1n,v2n)}⊂D(A),使得

且在H中,有

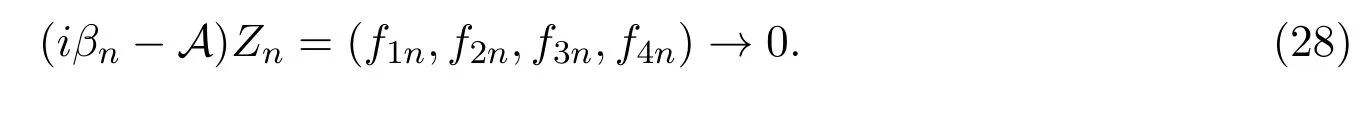
于是,在V中有,

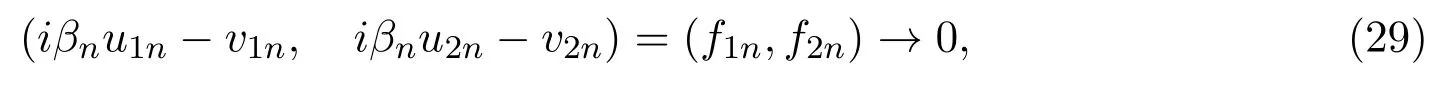
在H中有,

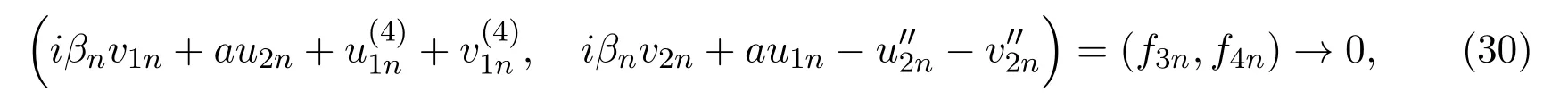
由(8)式可得:

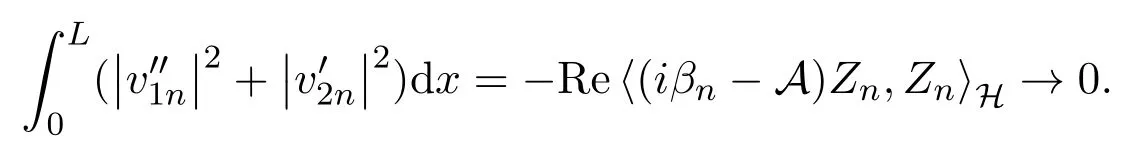
因此在L2(0,L)中有

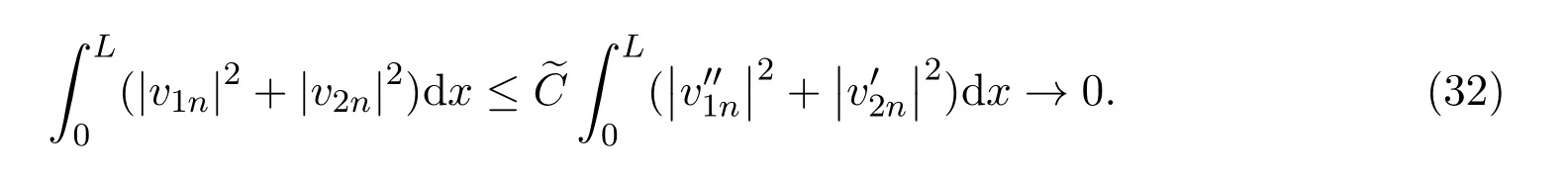
另一方面,由(29)式知,〈(f1n,f2n),(v1n,v2n)〉H→0,通过分部积分得,

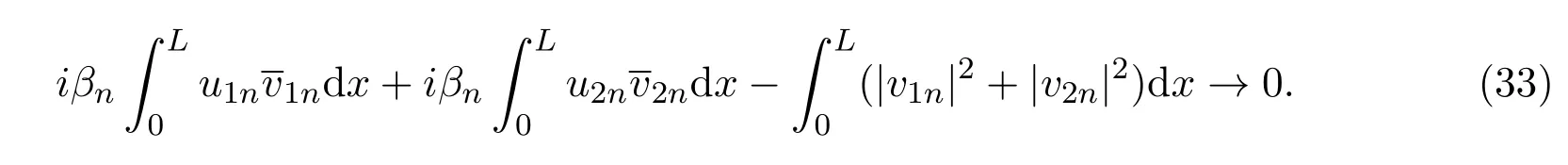
由(30)式知,〈(f3n,f4n),(u1n,u2n)〉H→0,通过分部积分并结合(31)式得,

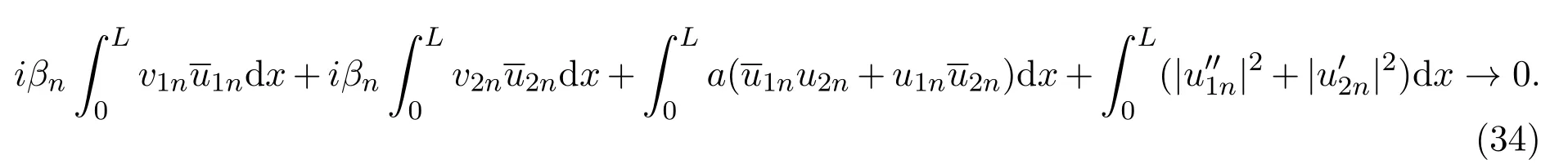
将(33)和(34)两式相加,并取实部得:

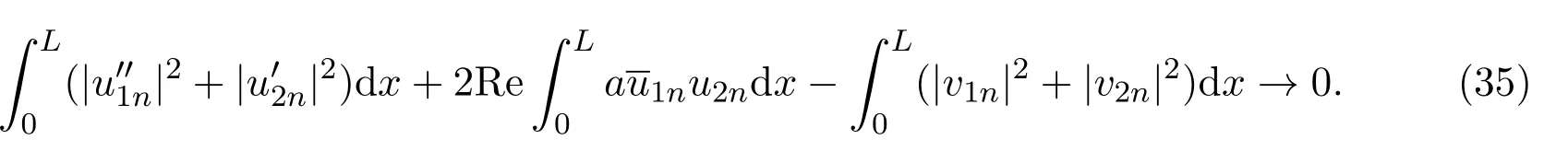
又由(29)结合(27)式得到:在L2(0,L)中有,u1n→0,u2n→0,于是结合(H1),有

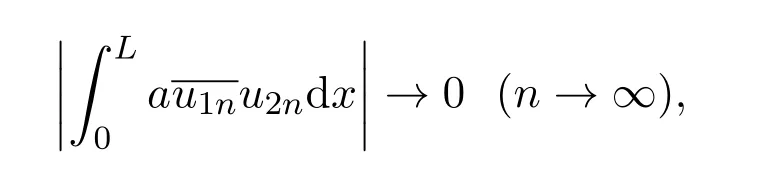
从而由(35)结合(27)式得到:

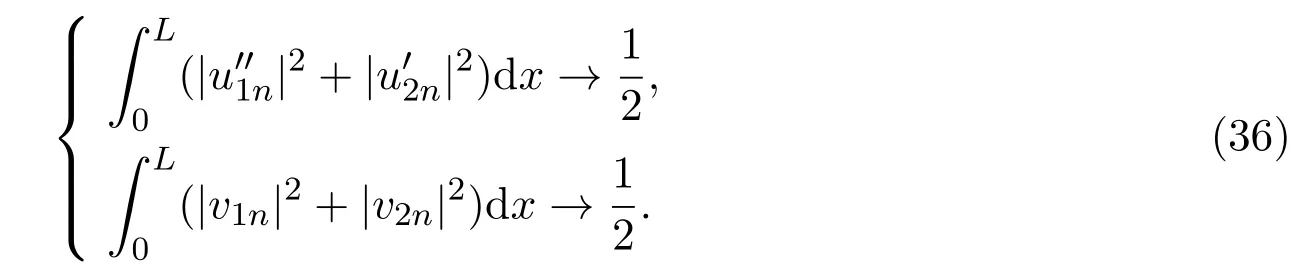
于是(36)的第二式与(32)式矛盾.这就证明了定理2.2.

[1]Aissa Guesmia.Energy decay for a damped nonlinear coupled system[J].Journal of Mathematical Analysis and Applications,1999,239:38-48.

[2]Han X S,Wang M X.Energy decay rate for a coupled hyperbolic system with nonlinear damping[J]. Nonlinear Analysis,2009,70:3264-3272.

[3]Han X S,Wang M X.General decay of energy for a viscoelastic equation with nonlinear damping[J].Math. Meth.Appl.Sci.,2009,32:346-358.

[4]Liu K S,Liu Z Y.On the type of semigroup associated with the abstract linear viscoelastic system[J].Z. Angew.Math.Phys.,1996,47(2):1-15.

[5]Liu K S,Liu Z Y.Exponential decay of energy of vibrating strings with local viscoelasticity[J].Z.Angew. Math.Phys.,2002,53(2):265-280.

[6]Liu K S,Liu Z Y.Exponential decay of energy of the Euler-Bernoulli beam with locally distributed Kelvin-Voigt damping[J].SIAM J.Cont.Optim.,1998,3(36):1086-1098.

[7]Pazy A.Semigroups of Linear Operators and Applications to Partial Dif f erential Equations[M].New York: Springer-Verlag,1983.

[8]Huang F L.Characteristic condition for exponential stability of linear dynamical systems in Hilbert spaces[J]. Ann.of Dif f.Eqs.,1985,1(1):43-56.

[9]Adams R A.Sobolev Spaces[M].New York:Academic Press,1975.

[10]Chen S P,Liu K S,Liu Z Y.Spectrum and stability for elastic systems with global or local Kelvin-Voigt damping[J].SIAM J.Appl.Math.,1998,2(59):651-668.

Energy decay estimates for the weakly coupled systems with Kelvin-Voigt damping

Fan Meili,Zhang Chunguo,Gu Shangwu
(Department of Mathematics,Hangzhou Dianzi University,Hangzhou310018,China)

This paper studies the weakly coupled systems with Kelvin-Voigt damping.First,under the appropriate hypothesis,we prove the well-posedness of the system by using the theory of linear operator semigroup. And then,we show that the energy of the weakly coupled system with Kelvin-Voigt damping is uniform exponential decay by applying the frequency domain result on Hilbert space.

Kelvin-Voigt damping,weakly coupled system,linear operator semigroup, uniform exponential decay

O231.4

A

1008-5513(2014)06-0634-08

10.3969/j.issn.1008-5513.2014.06.013

2014-07-31.

国家自然科学基金(61374096,11271104).

樊美丽(1989-),硕士生,研究方向：分布参数系统.

2010 MSC:35B37,93B52