基于中值-半宽（M-H）的区间多属性决策方法

胡 钢,吴传良,唐 亮

(安徽工业大学管理科学与工程学院,安徽马鞍山243032)

基于中值-半宽（M-H）的区间多属性决策方法

胡 钢,吴传良,唐 亮

(安徽工业大学管理科学与工程学院,安徽马鞍山243032)

从不确定区间数的中值与半宽角度出发研究属性权重信息完全未知且属性值以区间数形式给出的多属性决策问题。文中给出区间数定义，构建中值-半宽（M-H）区间数排序方法与运算法则；给出基于（M-H）区间数决策矩阵的规范化方法，依据决策方案与理想方案的关联系数离差最大化原则，提出求解属性权重的优化方法，并通过实例验证了该方法的实用性和有效性。

多属性决策;区间数;规范化;排序方法;运算法则

多属性决策越来越广泛地应用于工程设计、投资决策、项目评估、工厂选址等领域。由于客观情况的复杂多变性以及主观思维的不确定性,决策者往往不能给出属性权重信息，且给出的属性值常以区间数而不是具体数据的形式表示，对于这类问题的研究主要涉及3个方面：1）数据的处理，特别是区间数决策矩阵的规范化；2）属性权重的确定；3）根据区间数综合属性值确定方案的排序。对于规范化问题，Moore R等[1]在数字决策矩阵规范化的基础上做适当改进，但没有充分利用区间数决策矩阵的特性；樊治平等[2]、刘树林等[3]基于误差传递的规范化方法，适用性较差；徐泽水等[4]、胡钢等[5]从主观和客观两个方面进行属性权重研究。排序问题主要解决对区间数的排序，其中周光明等[6]给出M-V的方法简单实用，徐泽水等[4,7-8]给出基于可能度的排序方法。这些研究中区间数用上下限的形式来表示。于少伟等[9]基于信息中值与半宽给出动态区间系统鲁棒性测度分析，但未对区间信息的中值半宽偏好信息进行预处理，且对信息集结提取方式没有深入分析。本文采用对区间数偏好信息提取与集结方式——中值和半宽（M-H）形式对多属性决策问题进行研究。

1 区间数定义及排序

定义1记a=[aL，aU]={x|0＜aL≤x≤aU，aL，aU∈R},称a为一个区间数。

显然,当aL=aU时,区间数a退化为实数。

周光明等[6]提出关于不确定性决策中区间数的一种期望－方差(E-V)排序方法，这里的期望值即是区间数的中点值，方差的大小代表了区间数信息的不确定程度，因此可以用 w(·)来代替方差。设，建立如下M-H优先序关系：

定义2a优于b是指以下两种情形之一发生：1)m(a)＞m(b);2)m(a)=m(b)且w(a)＜w(b)。

定义3a等价于b是指m(a)=m(b)且w(a)=w(b)。

定义4a劣于b是指以下两种情形之一发生：1)m(a)＜m(b);2)m(a)=m(b)且w(a)＞w(b)。把a优于b记作a≻b，a等价于b记作a～b，a不劣于b记作a≥b，a劣于b记作a≺b。显然以上定义的区间数的偏序序关系具有传递性、连通性。

2 区间数运算法则

现有的区间数二元运算关系都是针对上下限形式表示的区间数给出的，本文给出针对中点半宽形式表示的区间数给出区间数的二元运算关系如下：

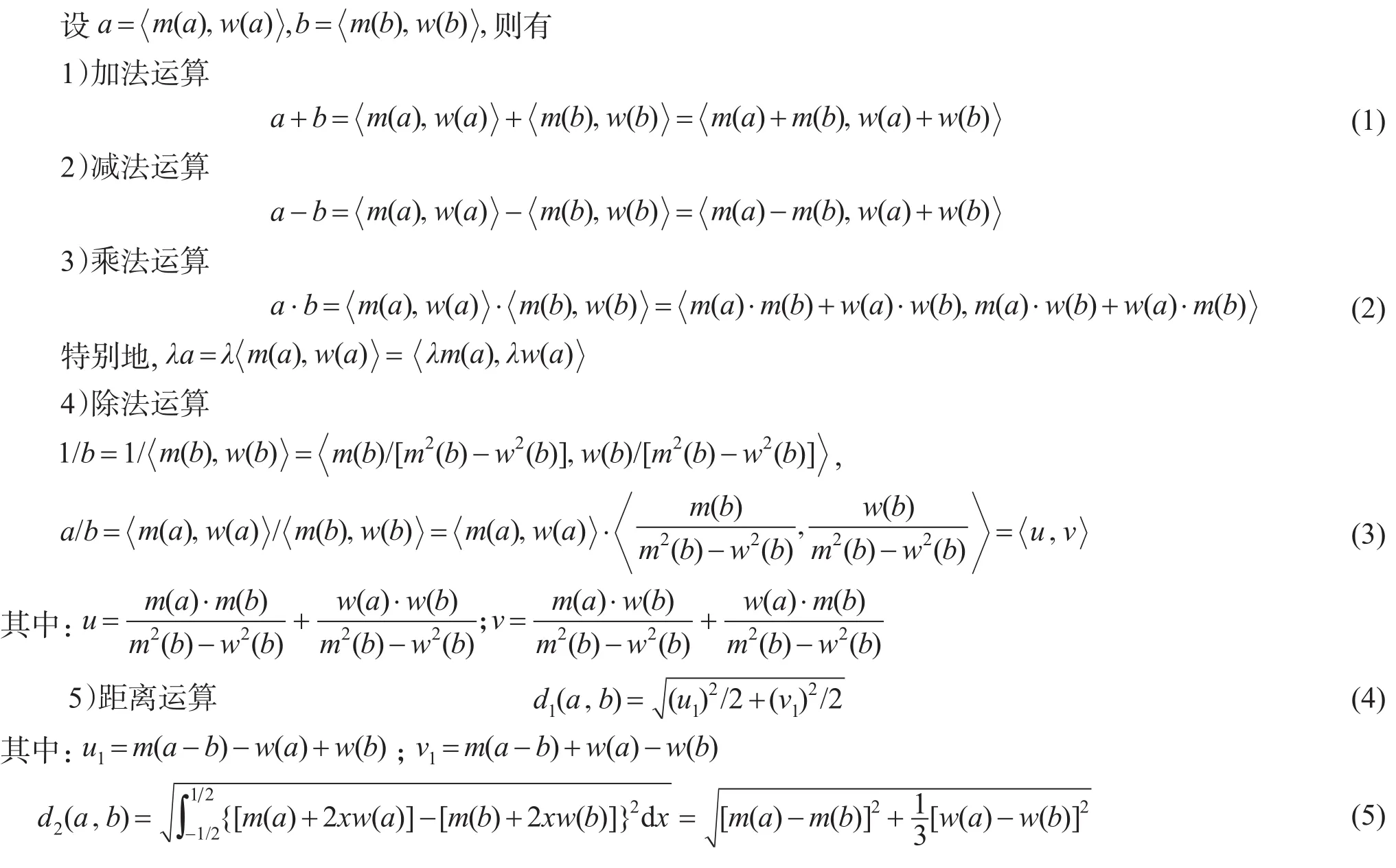
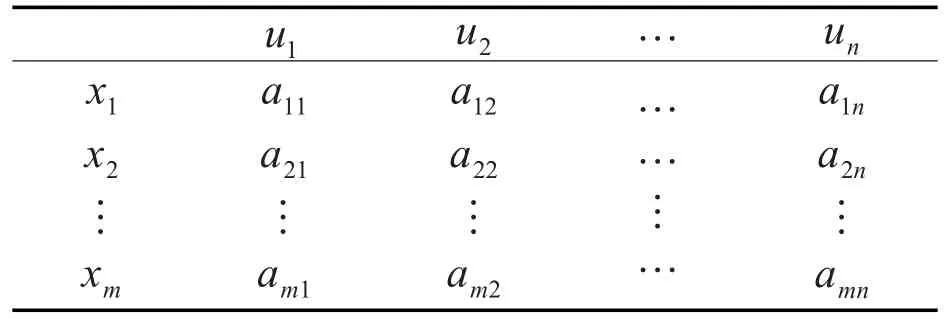
表1 决策矩阵Tab.1Decision-matrix

3 区间数多属性决策

属性集U中有效益型和成本型两种类型属性。效益型属性其值越大越好；成本型属性其值越小越好。设I1和I2分别表示效益型和成本型属性的下标集。

3.1 区间数决策矩阵规范化处理方案

为消除各属性的不同物理量纲对决策结果的影响，先对决策矩阵进行规范化。这里基于区间数的中点和半宽给出区间数决策矩阵的规范化方法。

1)中值决策矩阵规范化

2)半宽矩阵规范化

3)标准化

因为r1ij，r2ij∈[0，1]，所以m(ij)-w(ij)∈[0，1]，m(ij)+w(ij)∈[0，1]，则=(ij)m×n为规范化的区间数决策矩阵。

3.2 决策方法

定义4称R+={r1+，r2+，…，rn+}为区间型理想方案，其中rj+=1，0。

定义5方案xi和区间型理想方案R+关于指标uj的关联系数为

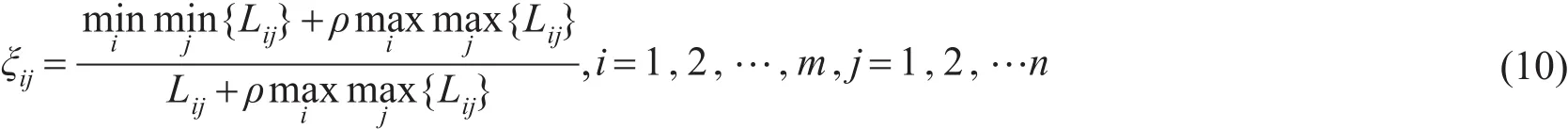
其中Lij为区间数ij到r+j的距离，这里的距离采用第2节给出的区间数距离公式，ρ为分辨系数，ρ∈[0，1]，一般取值0.5。

各方案与理想方案的关联系数矩阵为

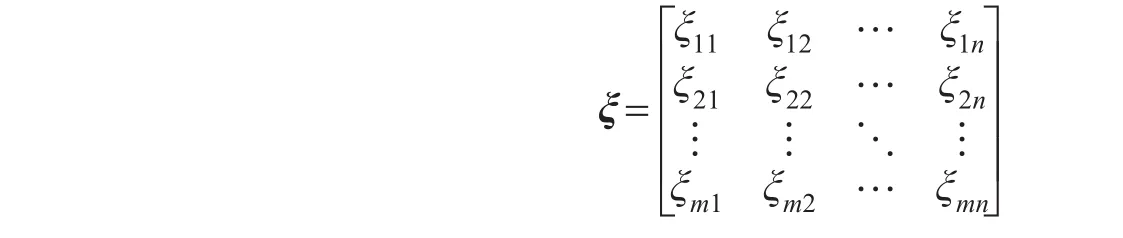
为确定第 j个指标uj的权重，建立下面最优化模型：

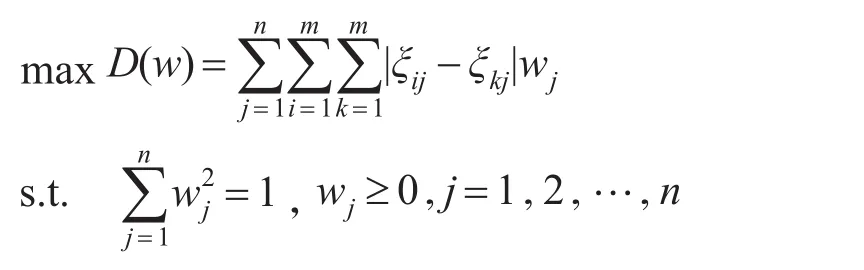
该最优化模型意义在于：指标权重的确定取决于该指标下所有方案与理想方案关联度的离差程度，若其离差程度越大，则说明所有方案的指标值的离差程度越大，则该指标对方案排序所起的作用越大，应赋予较大的权重；反之，则应该赋予较小的权重。通过求解最优化模型，并归一化得

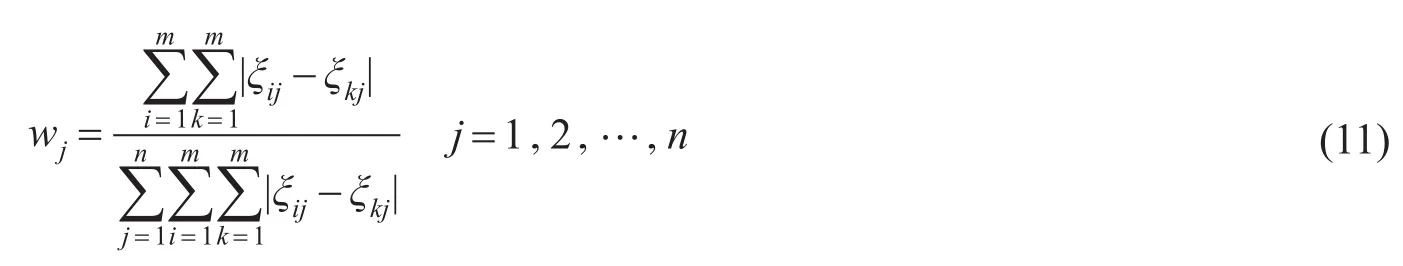
根据多属性决策分析中的加权法,令

基于上述讨论，给出具体的算法如下：

Step1根据决策问题构造决策矩阵A=(aij)m×n，并利用提出的规范化方法把其转变为规范化决策矩阵

Step4根据式(12)求得各个方案的综合属性值，并利用M-H方法对方案进行排序择优。

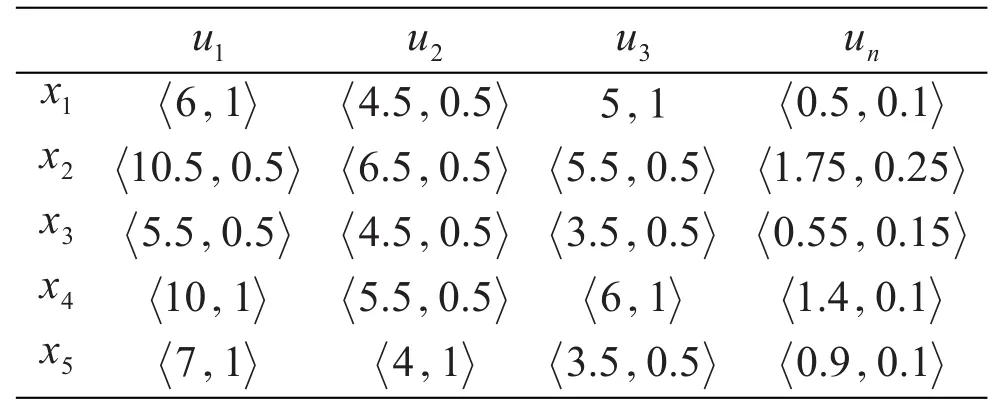
表2区间数决策矩阵ATab.2 M axtrix of interal-number decision

4 实例分析

采用文献[8]提供的数据验证所提出的决策方法合理性。为开发新产品，对五个投资方案进行选择。有4项评价因素(属性)：投资额(u1)，期望净现值(u2)，风险盈利值(u3)，风险损失值(un)。其中投资额和风险损失值为成本型属性，期望净现值和风险盈利值为效益型属性。区间数决策矩阵见表2。

由式(6)、(9)计算规范化中值矩阵R1

由式(8)计算规范化半宽矩阵R2

用式(11)求得最优权重向量

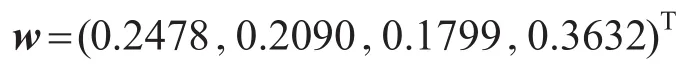
由式(12)求得方案的综合属性值分别为

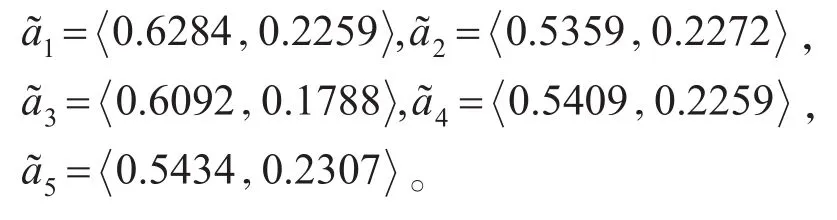
利用M-H方法对方案进行排序易得：x1≻x3≻x5≻x4≻x2。因此x1具有较大的投资价值。

5 结 语

针对属性权重信息完全未知、且属性值以区间数给出的区间数多属性决策，给出了基于中值半宽（M-H）区间数不确定偏好信息的提取、融合、规范化以及排序新方法。该方法简洁、直观、便于计算，为多属性区间网络决策、区间系统多顺序时段动态决策提供新的理论根据与方法。

[1]Moore R,Lodw ickW.Intervalanalysisand fuzzy set theory[J].Fuzzy Setsand Systems,2003,135:5-9.

[2]樊治平,宫贤斌,张全.区间数多属性决策中决策矩阵的规范化方法[J].东北大学学报,1999,20(3):326-329.

[3]刘树林,邱菀华.多属性决策基础理论研究[J].系统工程理论与实践,1998,18(1):38-43.

[4]徐泽水,达庆利.区间数排序的可能度法及其应用[J].系统工程学报,2003,18(1):67-70.

[5]胡钢,冯向前,魏翠萍等.区间数判断矩阵满意一致性递推排序方法研究[J].山东大学学报：理学版,2007(11):89-93.

[6]周光明,刘树人.不确定多属性决策中区间数的一种新排序法[J].系统工程,2006,24(4):115-117.

[7]徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2004.

[8]徐泽水,孙在东.一类不确定型多属性决策问题的排序方法[J].管理科学学报,2002,5(3):35-39.

[9]于少伟,史忠科.基于正态分布区间数的逆向云新算法[J].系统工程理论与实践，2011(10):2021-2026.

责任编辑：丁吉海

NovelMethod for theM id-pointand Half-w idth IntervalMultiple Attribute Decision Making

HUGang,WU Chuanliang,TANG Liang
(School of Management Science&Engineering,Anhui University of Technology,Ma'anshan 243032, China)

Multipleattribute decisionmaking problemswith intervalnumbers isstudied from theview of themid-point and half-w idth of indefinite interval numbers,in which the information about the attribute weights is unknown completely.Firstofall,rankingmethod and operation rulesof intervalnumbersare instituted.Then new formula for normalizing the decisionmatrixw ith intervalnumbers isgiven.Furthermore,anew method forobtaining the attribute weights is proposed based onmaxim izing deviation of connection coefficientbetween each scheme and the ideal scheme.Finally,a numericalexample isgiven to show the feasibility and effectivenessof themethod.

multipleattributedecisionmaking;intervalnumbers;normalization;rankingmethods;operation rule

C934,O223

A

10.3969/j.issn.1671-7872.2014.01.021

1671-7872(2014)01-0094-05

2012-10-25

安徽省自然科学基金项目(KJ2011Z035)；安徽省社科规划项目（AHSK11-12D74）

胡钢(1970－),男,甘肃天水人,博士,副教授,研究方向为物流工程、决策分析。