基于用户移动性的认知网络频谱移动管理的数学建模

胡丽华，陈晓光

基于用户移动性的认知网络频谱移动管理的数学建模

胡丽华，陈晓光

针对IEEE802.22的无线地域网（WARN），首次，建立了考虑用户移动性的认知无线网络频谱移动管理的数学模型，更加真实地描述了认知无线网络中的用户行为，利用马尔科夫模型对提出的系统进行了仿真与分析。在此基础上，为了改善系统性能，还提出了带有切换保护信道的马尔科夫模型。

认知无线网络；频谱移动管理；马尔科夫模型；用户移动性；切换保护信道

0 引言

认知无线网络（cognitive radio network，CRN）的提出是为了能够有效地提高频谱利用率。在CRN技术中需要注意的是频谱移动性。频谱移动性是指当用户需求或外部环境发生变化而导致原先使用的频段变成不可用时，需要重新选择一个合适的可用频段，这个过程也称为频谱切换。在认知无线网络中，频谱切换通常发生在两种情况下：一是当某一频段被主用户（Primary User，简称PU）重新使用时；二是当前频段无法满足次用户（Secondary User，SU）QoS时，此时工作于该频段的次用户需切换到其他频段。

使用MARKOV模型来模拟PU和SU的行为，是一种常见的有效的方法。文献[1]中，Tang等人提出了一种 PU优先的MARKOV模型，当PU出现并随机接入一个正在被次用户使用的信道时，SU必须退让出此信道，因此会产生次用户掉话的情况。文献[2]中，Kondareddy等人利用三维连续时间MARKOV对系统的不同状态进行建模。文中引入了信道切换机制，当PU出现在正在被SU使用的信道上，SU退出并可继续在其他空闲信道上继续进行传输，因此，有效的提高了 SU的掉话率。Kondareddy等人还在文献[3]中提出了一种非随机信道接入机制，即将信道进行编号，到来的PU从最小编号开始分配信道，而到来的SU则从最大的编号进行分配。当无可用信道时，PU到来时，选择被SU使用的最大编号的信道，还在文献[3]认为此SU被服务的时间最久，但这种方法没有考虑到，若在最大编号的信道上被服务的最初那个SU已结束服务，而被打断服务的就不是最初那个被认为是服务时间最久的SU。文献[4]中，林威等人运用MARKOV模型分析并比较了基本频谱接入策略，频谱切换策略和信道预留接入策略，并仿真分析比较了3种策略的性能。

然而在上述文献当中都只针对因为主用户的出现而导致的频谱移动的变化，并没有考虑因次用户移动引起的频谱移动性。预留的信道也是针对主用户，虽然相较于基本信道接入，使用信道预留能够降低次用户的阻塞率和切换掉话率，但并未充分利用所有信道。针对上述问题，为了更加真实描述认知无线网络中的PU和SU的行为。本文中考虑了次用户的移动性，引入了业务平衡流模型，利用MARKOV模型进一步更加真实的描述了PU和SU的行为。

1 考虑用户移动性的建模

基于802.22的WRAN系统，如图1所示：

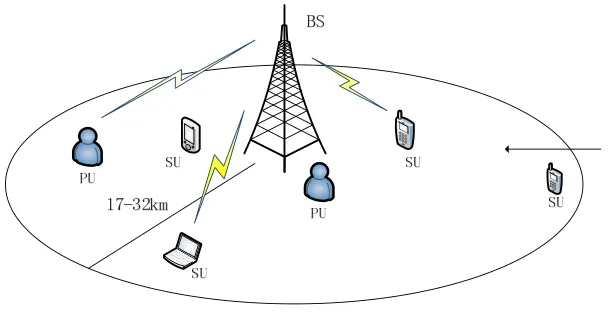
图1 WRAN网络小区

WRAN系统包括一个基站和多个用户驻地设备包括主用户和次用户等认知用户。其中，一般认为主用户固定的，次用户是移动的。

1.1 次用户业务平衡流模型

在提出的WRAN模型中，业务平衡流模型只考虑次用户业务流入流出。假设次用户新发起的服务平均到达率为λs，服务持续时间Ts并服从参数为μs 的指数分布，则服务时间概率密度函数为次用户因移动而产生的移动切换业务平均到达率为λh，在给定小区内的驻留时间 Th 服从参数为的指数分布，则平均驻留时间为

在一个给定小区里某个信道的保持时间为 Tc，平均信道保持时间

定义上面3个独立的随机变量的各种分布函数，分别为

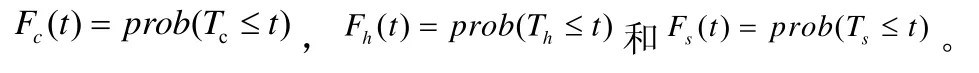
根据初等概率论，则有下面的关系，如公式（1）、（2）：

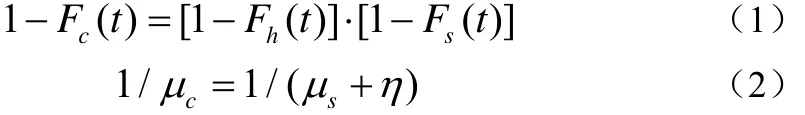
现在讨论次用户业务流平衡模型。假设移动密度均匀，小区的几何形状和终端移动速度一样。次用户新发起的业务为，为一个新业务被阻塞的概率。次用户的平均切换率为λh，一个切换请求由于新的小区缺少可用信道而被拒绝的概率为，从简单的业务流量平衡角度来看，离开小区的平均数和获得信道的呼叫数 λh 等于跨小区切换的平均数，如图2所示：

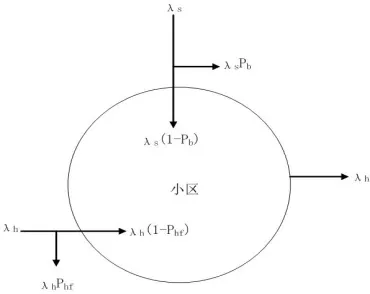
图2 次用户业务流量的变化

小区流量平衡方程：

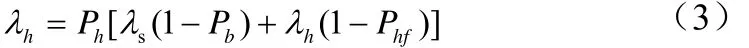
根据公式（3）可得公式（4）：

当次用户服务时间大于小区驻留时间时，将发生切换，则得公式（5）：

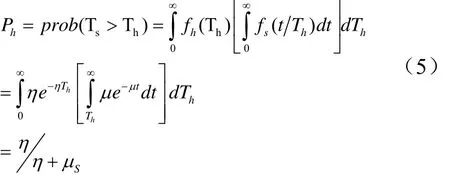
1.2 主用户和次用户行为建模

采用三维连续时间马尔科夫模型（3D-CTMC）对 PU和SU的行为进行建模，如图3所示：

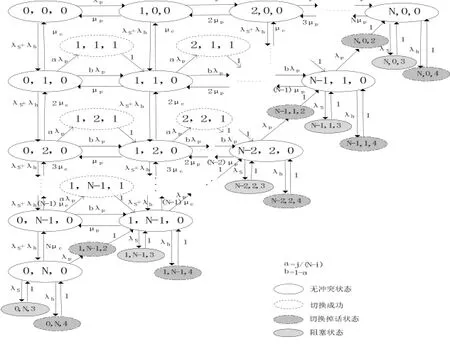
图3 认知无线网络中用户的3D-CTMC模型

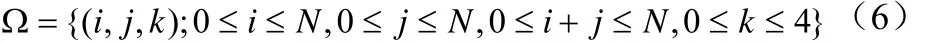
其中i， j分别表示系统中正在接受服务的 PU和 SU数目，k表示发生的事件。其中，k=0表示主用户和次用户无冲突；k=1表示次用户因主用户出现且系统中有可用信道，则切换成功；k=2表示次用户因主用户出现而小区中无可用信道发生切换掉话；k=3表示次用户到来因无可用信道发生阻塞；k=4表示从其他小区切换来的次用户因本小区中无可用信道而发生切换掉话。

例如(0,0,0)表示系统中无主用户也无次用户，则两者不发生冲突。(0,N,0)表示系统中有N个次用户正在进行服务，即无其他可用信道。若此时主用户到来，其中一个次用户会因系统中无其他可用信道而发生掉话则变成即转换到状态(1,N-1,1)，且以概率1转换为(1,N-1,0)；若此时有次用户的新业务到达，则发生阻塞，转换到状态(0,N,3)；若此时从其他小区有次用户业务切换过来，会因本小区无可用信道而发生切换掉话，转换到状态(0,N,4)。例如说明系统中存在有可用信道，当系统处于状态，此时主用户出现随机接入信道。会有两种情况出现，一以概率a接入正在被次用户使用的信道，则此次用户会切换到其他信道上，且出现状态；二以概率b接入其他空白信道，则直接进入状态，其中

3D-CTMC模型有如下平衡方程，如公式（7）-（15）：当

Ω状态空间表示为公式（6）：

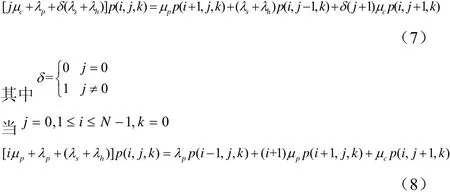
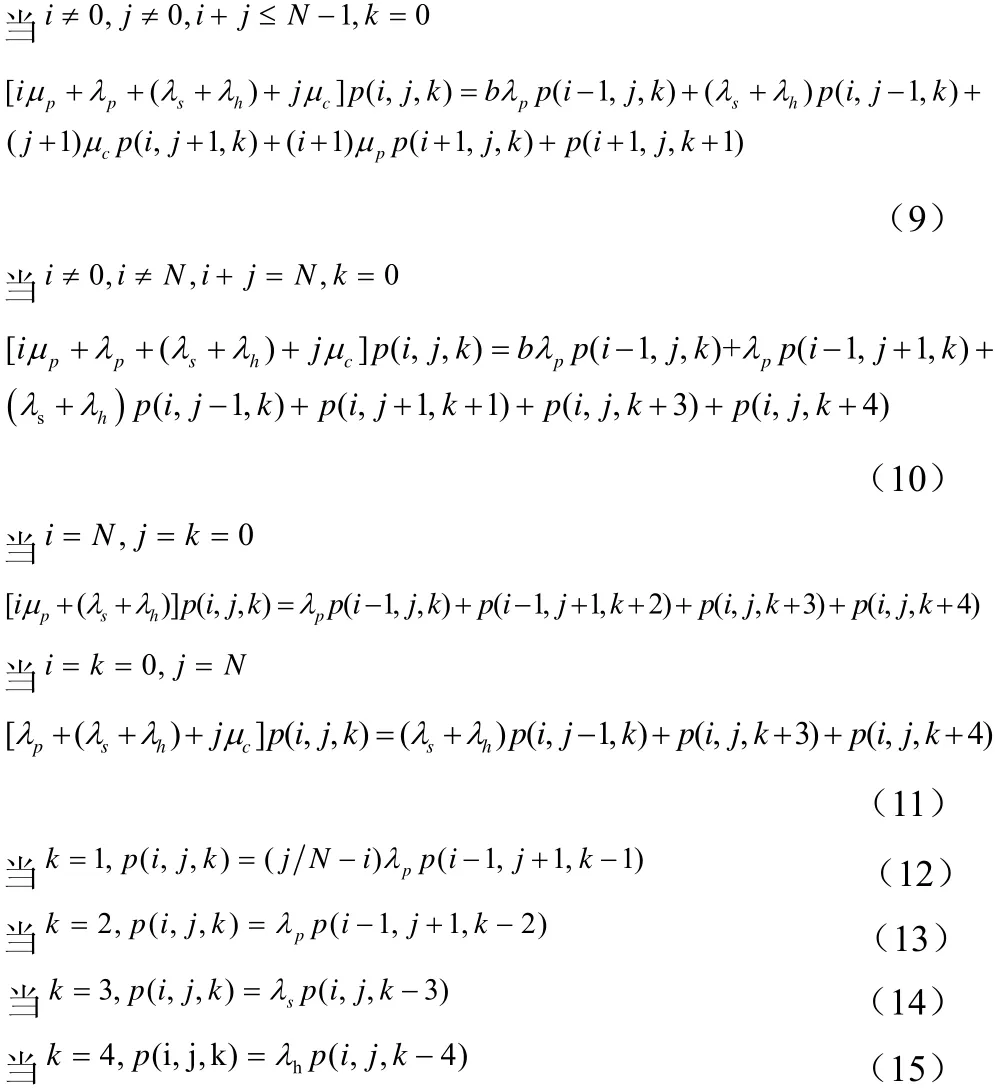
从图3中可看出，k=1,2,3,4的状态都会以概率1（速率∞）进入下个状态，说明这些状态都是瞬态的，存在时间极短，可以忽略不计[4]。所以为了更加方便计算，可以对其进行修正为2D-CTMC模型，如图4所示：

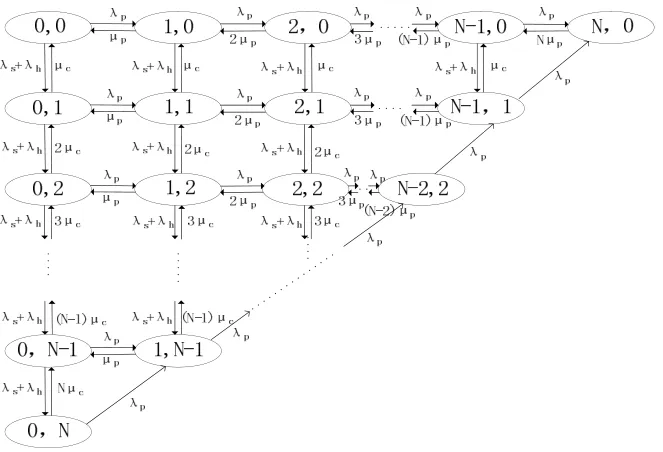
图4 2D-CTMC带切换频谱接入稳态模型

采用2D-CTMC对PU和SU的行为进行建模，状态空间表示为公式（16）：

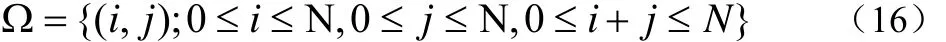
其中i，j分别表示系统中PU和SU的数目，表示系统处于状态(i, j)的稳态概率。

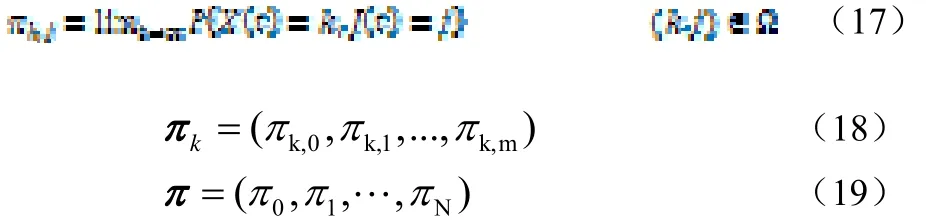
阻塞率为：

切换掉话率为：

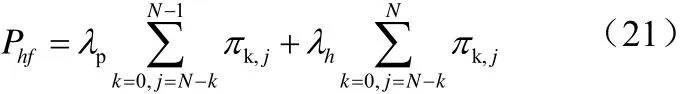
2 矩阵理论分析

矩阵几何法[7]作为研究随机模型的重要方法，可以求解多维马尔科夫模型的稳态概率。由图4可看出，此模型是个拟生灭过程( Qausi Birth And Death process，QBD)，其中生成元Q 形式为公式（22）-（25）：

根据矩阵几何法，有如下关系式，如公式（26）：

根据 Netus理论[8]，由 QBD 过程稳态的边界条件和，可得方程组，如公式（27）：

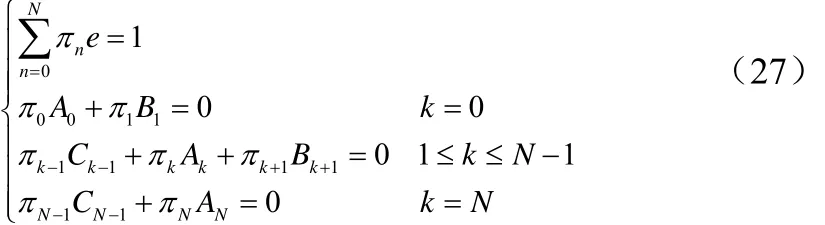
将转移矩阵Q的第一列替换为e，可记为 Q1，则有，因此可得到系统的稳态概率为。其代入公式（26）、（27），可求出系统阻塞率和切换掉话率。

3 仿真结果与分析

（1）次用户阻塞率和掉话率随次用户新业务 sλ变化

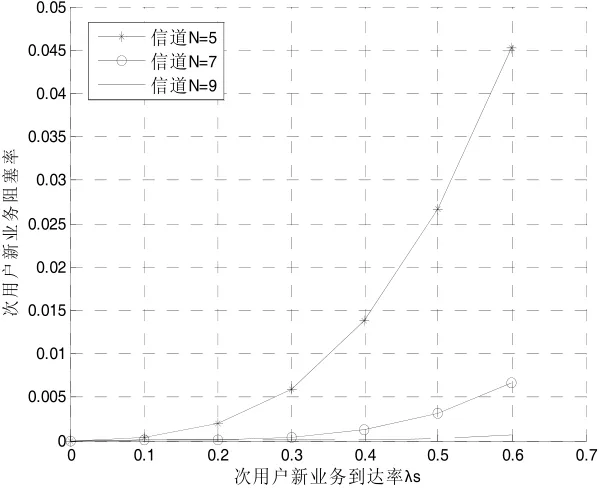
图5 次用户新业务阻塞率λS

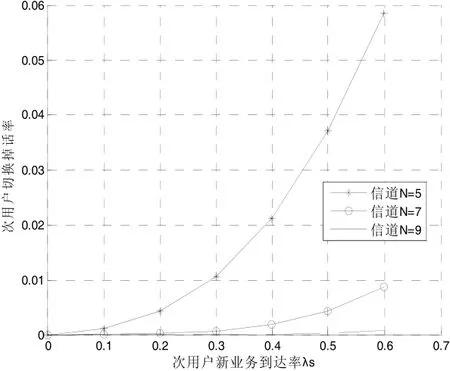
图6 次用户切换掉话率λS

从图5和图6中发现当系统中信道数为5时，随着次用户业务达到率每秒从从0.4个增加到0.5个，阻塞率升高了1%，而掉话率升高了2%左右。说明了次用户切换掉话率是影响次用户业务的重要因素。

（2）根据不同小区大小及移动业务流量，我们定义了一个相对切换因子a=小区信道数分别为5、7、9，=0.3个/秒，1/=1/0.4秒，=0.5个/秒，=个/秒，1/=1/0.6秒，则相对切换因子变化范围为a=0～2。次用户阻塞率和掉话率随次用户相对切换因子a的变化，如图7、图8所示：

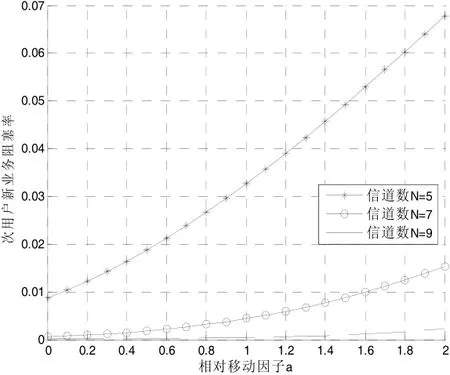
图7 次用户新业务阻塞率λS

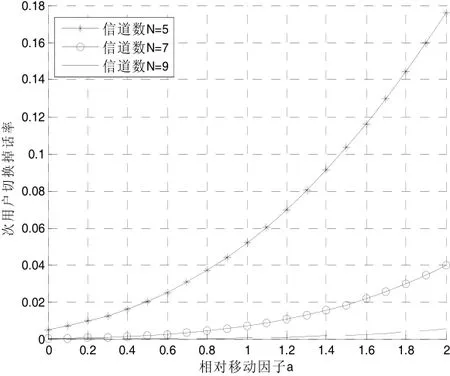
图8 次用户切换掉话率λS

从图7和图8中发现随着相对移动因子a的增大，次用户新业务阻塞率和切换掉话率都会有所增加，尤其是切换掉话率。当系统中信道数为5，相对移动因子a从0.8增加到1.2时，阻塞率增加了1.5%，切换掉话率则增加了3%左右。

4 总结

本文讨论了之前文献中所利用的马尔科夫模型的不足。文中利用了简单流平衡模型首次提出了考虑用户移动性的马尔科夫建模，这样更加真实模拟了现实生活中小区情形。并利用 matlab对次用户业务的阻塞率，掉话率随着次用户新业务到达率和切换业务到达率的变化进行了模拟仿真和分析。

[1] Tang P K, Chew Y H, Ong L C, et al. Performance of secondary radios in spectrum sharing w ith prioritized primary access[C]. M ilitary Communications Conference, 2006. M ILCOM 2006. IEEE. IEEE, 2006: 1-7.

[2] Kondareddy Y R, Agrawal P. Effect of dynam ic spectrum access on transport control protocol performance[C]. Global Telecommunications Conference, 2009. GLOBECOM 2009. IEEE. IEEE, 2009: 1-6 .

[3] Kondareddy Y R, Andrews N, Agrawal P. On the capacity of secondary users in a cognitive radio network[C]. Sarnoff Symposium, 2009. SARNOFF'09. IEEE. IEEE, 2009: 1-5.

[4] 林威, 付宇, 张钦宇, 等. 认知无线电中认知用户的重新建模与性能分析[J]. 通信学报, 2012, 33(11): 108-118.

[5] Wright, David. "Dynamic spectrum access in the IEEE 802.22 w ireless regional area network." Access Networks & Workshops, 2007. AccessNets' 07. Second International Conference on. IEEE, 2007.

[6] Jabbari B. Teletraffic aspects of evolving and next-generation w ireless communication networks[J]. Personal Communications, IEEE, 1996, 3(6): 4-9.

[7] 田乃硕, 岳德权, 运筹学. 拟生灭过程与矩阵几何解[M]. 科学出版社, 2002.

[8] Neuts M F. Matrix-geometric solutions in stochastic models: an algorithm ic approach[M]. Courier Dover Publications, 1981 .

[9] 张伟卫, 赵知劲, 王海泉. 基于预留信道机制的 CR频谱切换描述及改进[J]. Computer Engineering, 2010, 36(22).

Spectrum M obility M anagement M athematical M odel Based on User M obility in Cognitive Radio Networks

Hu Lihua , Chen Xiaoguang
(Department of communication science engineering, Fudan university, shanghai 200433, China)

For IEEE802.22 w ireless area network (WARN), this paper was established to consider user mobility of cognitive w ireless network spectrum mobility management for the first time. It described user’s behavior in cognitive radio network more realistically, and performance analysis of the proposed Markov model was presented. On basis of this, this paper also established another MARKOV model w ith handoff reservation channel to improve the performance.

Cognitive Radio Network; Spectrum Mobility Management; Markov Model; User Mobility; Handoff Reservation Channel

TN393

B

2014.08.15）

胡丽华（1990-），女，浙江杭州，复旦大学通信科学与工程系，硕士研究生，研究方向：认知无线电方向，上海，200433

陈晓光（1964-），男，安徽五河，复旦大学通信科学与工程系，副教授，研究方向：移动无线通信，上海，200433

1007-757X(2014)11-0049-04