最小残差法加速局部加权LSSVM求解及其应用
2014-07-24林超王华杰
林超,王华杰
最小残差法加速局部加权LSSVM求解及其应用
林超,王华杰
局部加权最小二乘支持向量机回归模型(LocalWeighted Least Squares Support Vector Machines ,LW-LSSVM)是一种在线学习模型,该类模型需要根据训练样本权重的调整不断重新进行训练。高效稳定的学习算法是LW-LSSVM模型取得成功应用的关键。分别采用最小残差法(M INRE)、共轭梯度法(CG)、零空间法和Cholesky分解算法求解WL-LSSVM模型。基准数据库上的数值实验表明最小残差法的计算时间最短,具有良好的数值稳定性。随后,应用基于M INRES的WL-LSSVM建立了高炉铁水硅含量的在线预测模型,仿真实验表明与LSSVM相比LW-LSSVM模型具有更高的预报精度和自适应性。
LSSVM;局部加权;最小残差法;铁水硅含量
0 引言
SVM是基于结构风险最小化原则建立的核学习模型[1]。随后学者们研究了SVM的多种变形,其中,Suykens等人建立的LS-SVM模型结构最为简单,并获得的广泛应用[2]。LS-SVM将SVM模型中的不等式约束替换为等式约束,同时,在目标函数中采用具有良好光滑性质的二次损失函数取代SVM模型中的不敏感损失函数。由于LS-SVM的最优性条件(KKT条件),可以转换为线性系统,无需求解二次规划问题,与SVM相比LS-SVM的求解更为简单、快速,更适合在线应用。
高炉炼铁过程是一个高度复杂的非线性过程,其实质是将铁从铁矿石等含铁化合物中还原出来。冶炼期间, 炉内将发生复杂的气-固、固-固、固-液相反应,并伴随有高温、高压、
多相共存、化学反应与传递现象同时发生等特点。高炉炼铁过程的复杂性造成了对其进行有效控制十分困难。长期以来,国内外研究人员根据高炉炼铁内部所发生的化学反应传递现象建立了多种数学模型[3],这些模型在理论上对于揭示高炉内部现象起了一定的积极作用,但也存在着准确性低等缺点。鉴于此,数据驱动建模方法正被广泛应用于高炉炼铁过程的实时模拟和控制。高炉在炼铁过程中,产生了丰富的在线和离线测量数据,如原料参数,包括铁矿石成份、焦炭负荷、喷煤速率、焦炭比等;鼓风参数,包括风量、风温、风压、富氧程度、鼓风湿度等;铁水成份参数,包括铁水硅含量、铁水硫含量等;炉渣成份、炉渣碱度以及透气性指数等,为实现高炉炼铁过程数据驱动建模提供了可能。目前,利用数据驱动的思想所建立的高炉预测及控制模型主要有神经网络模型[4]、非线性时间序列分析模型[5]、模糊模型[6]、贝叶斯网络模型[7]、偏最小二乘模型[8]、支持向量机模型[9]等。上述模型基本是全局离线型模型,模型关注的是模型的全局推广能力。此类模型在数据较充分的区域较为准确,而模型在数据不充分或变化较大的区域精度欠佳。刘毅等学者,引入局部学习的思想,建立了待测样本点附近的局部模型[10]。相关的研究表明,与全局学习相比,局部学习能有效提高建模精度[10,11]。
本文在现有对高炉炼铁过程 LS-SVM 模型研究的基础上,基于样本点的欧式距离构造了一种相似性度量准则,计算样本点的相似性,并由此确定样本点的惩罚权重因子。基于惩罚权重因子建立了局部加权最小二乘支持向量机回归模型(LocalWeightedLeast Squares Support Vector Machines,LW-LSSVM),实现了样本权重的在线调整。随后,应用LW-LSSVM对高炉铁水硅含量进行在线建模,仿真结果表明,LW-LSSVM较离线LSSVM有着更高的预测精度、更好的泛化能力,能更好的描述高炉冶炼过程这样一个动态时变系统,适合高炉铁水硅含量的在线建模。此外,考虑到在线应用的实时性要求学习模型具有较快的计算速度,我们提出采用M INRES算法求解LW-LSSVM模型。基准数据集上的数值试验表明,与当前主流的CG算法和零空间算法相比,M INRES算法能显著提高LW-LSSVM模型的求解效率。
1 LW-LSSVM模型与求解算法
1.1 LSSVM回归模型
LSSVM回归模型是基于数据的机器学习方法,研究从观测数据(样本) 出发寻找规律,利用这些规律对未来数据或无法观测的数据进行预测。给定训练样本集,LSSVM的决策函数满足如下形式其中,特征映射可将输入样本x映射到特征空间,b是截距项,w则是特征空间中的权重向量。LSSVM模型可表示为如下二次规划问题,如公式(1):
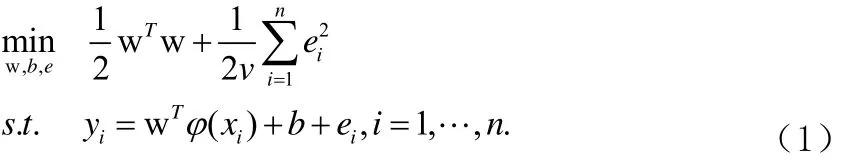
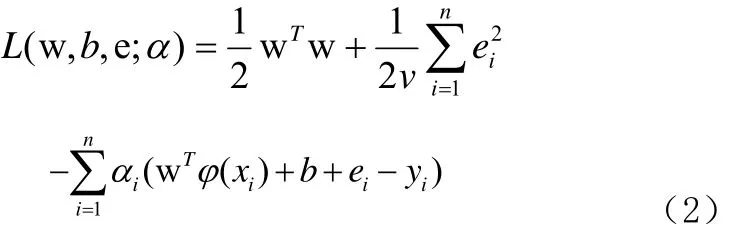
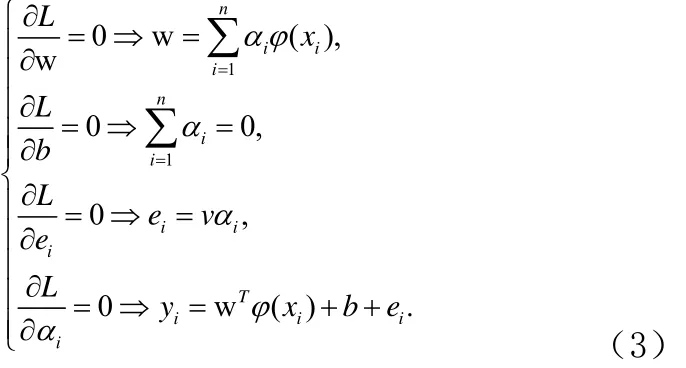
消掉变量w和误差变量e,KKT系统可表示为线性方程组,形式如公式(4):
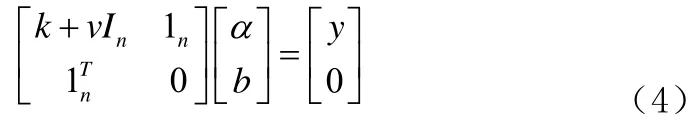
1.2 LW-LSSVM模型与求解
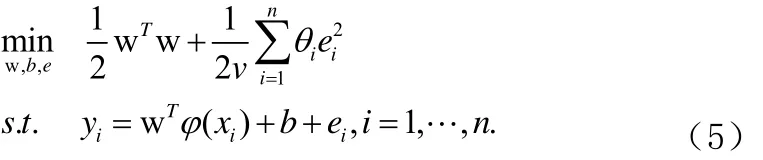
LW-LSSVM模型对应的 KKT系统可以描述为如下鞍点系统,如公式(6):
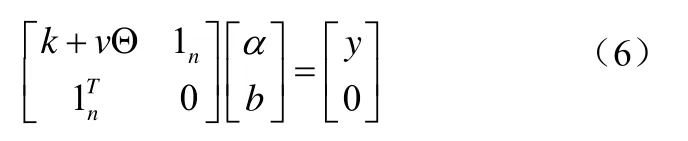
共轭梯度法:类比Suykens等人的工作[12],采用迭代策略,应用共轭梯度法迭代求解如下正定系统,如公式(7):系统(6)可转换为正定系统

得到中间变量μ和η,随后可得原鞍点系统(6)的解
零空间法:应用 Chu等人采用的零空间法[13],将鞍点系统转(6)表示为,设系统的特解为并设的零空间为通过共轭梯度法求解正定系统,得到中间变量λ,进而可得鞍点系统(6)的解
Cholesky分解法:考虑到线性系统(7)的特殊结构[14],首先使用Cholesky分解算法分解对称正定矩阵H,即利用 Cholesky因子L高效求解正定系统(7)得到中间变量μ和η,进而求得原鞍点系统的解
MINRES算法:Paige和Saunders提出的最小残差法是求解对称非正定系统的高效算法。针对鞍点系统(6)的特殊结构,我们采用最小残差法迭代求解该系统。为了便于描述,简记鞍点系统为假设0x是系统的初始解,利用Lanczos方法[15]可得到迭代点列,满足:其中是第m个Krylov子空间。M INRES算法的相关收敛性分析可参考文献[15].
2 仿真实验
对于LW-LSSVM模型而言,模型权重的确定至关重要,将直接决定模型效果。考虑到在工程技术领域RBF函数经常被选取用于构造样本点的相似性,本文基于样本点的欧式距离,利用RBF函数构造样本相似性其中,核宽σ取为样本点的输入维数,并通过如下变换得到取值范围是的惩罚加权因子。本文中所有数值试验均是在MATLAB 7.14 环境下运行的,计算机配置为3.4 GHz Intel Core i3 处理器,4 Gb 内存,Windows 7操作系统。
2.1 基准数据库实验
首先,我们考察LSSVM模型和LW-LSSVM模型,以及四种算法共轭梯度算法(CG)、零空间算法(Null)、Cholesky分解算法(Cholesky)和最小残差算法(M INRES)在基准数据集上的性能表现。本文选取回归分析领域常用的误差均方根(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE)以及计算时间(CPU)作为评价指标衡量模型及算法的性能。性能指标RMES和MAE的计算公式如公式(8)、(9):
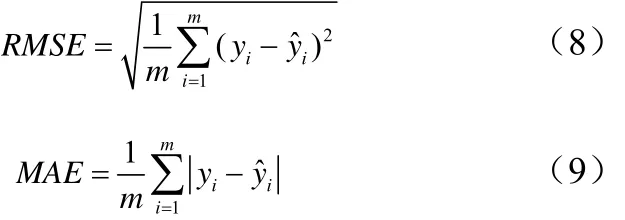

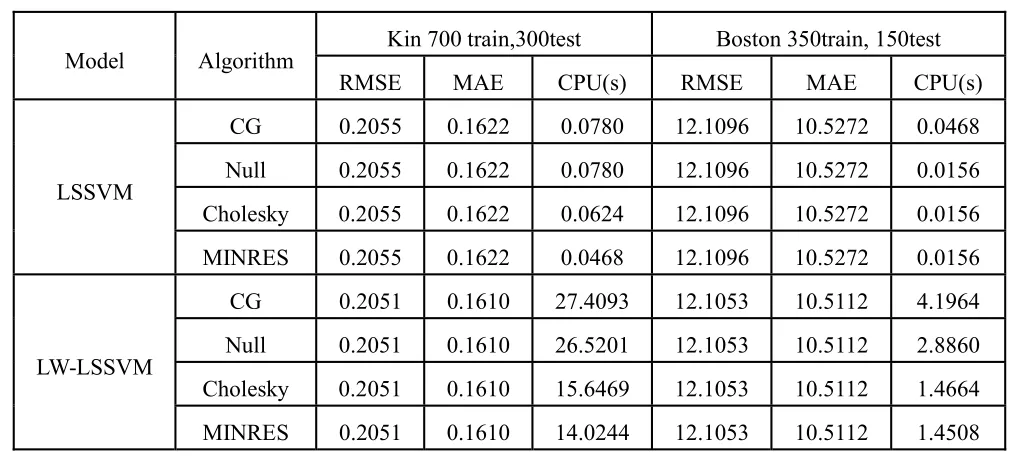
表1 基准数据集上的预测结果
由表1可以看到,与LSSVM模型相比,由于局部加权的LSSVM模型中加入了待预测样本与训练样本的相似性信息,LW-LSSVM模型的 RMSE的 MAE均有所提高。LW-LSSVM模型需要根据待预测样本不断调整惩罚加权因子 iθ,模型的训练次数为预测样本数,而LSSVM模型仅需训练一次。因此,与LSSVM相比LW-LSSVM的运行时间较长。四种求解算法CG、Null、Cholesky和M INRES对应的REMS和MAE完全相同,表明四种算法的数值稳定性较好。而运行时间一栏表明,Cholesky分解算法和 M INRES算法的计算速度相当,明显优于目前主流的共轭梯度算法和零空间算法。
2.2 高炉铁水硅含量预测
本段我们应用LSSVM模型和LW-LSSVM模型处理工业应用问题-高炉铁水硅含量预测问题,并比较四种算法的性能。
高炉炉温是影响高炉冶炼过程的关键参数。高炉冶炼过程具有高度复杂性与封闭性,很难直接测量炉缸温度场的分布。由于铁水硅含量([Si])与炉缸温度密切相关,冶金界通常用[Si] 的变动来间接反映炉缸温度场的变化。以莱钢1号高炉(容积750m3)在线采集的工业数据作为应用案例。考虑到生产过程数据的采集条件及其与[Si]的相关程度,选取了6个主要影响因素进行建模。模型输入变量分别为:上一炉铁水硅含量、上一炉铁量差、透气性指数、喷煤量、风温和风量。以上输入变量在数量级上差异巨大,因此采用数据标准化处理公式(10)对输入数据进行预处理。选取 RBF函数作为模型中的核函数,其中核宽参数σ设为6,模型正则化参数v设为1。本实验共采集样本数据1008组,其中前908组数据用于构造训练集,序号为No.31919~No.32018炉次的 100组数据构造测试集。[Si]时间序列,如图1所示:

图1 莱钢1号高炉铁水硅含量时间序列图
预测命中率是冶金生产中用来衡量模型优劣的重要指标,其定义如公式(11)所示:
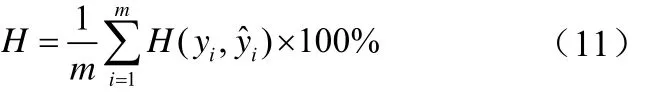
衡量模型性能的常用指标预测成功率的定义如公式(13)所示:
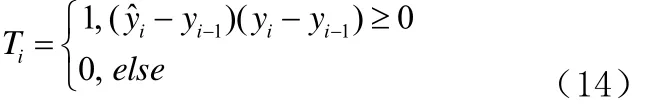
LW-LSSVM模型在均方根误差(RMSE)、预测命中率(H,%)、以及预测成功率(S,%)3个评价指标上的性能表现均优于LSSVM模型。表明相比于全局模型,局部加权LSSVM模型能更好的追踪时变系统的变化。在运行时间方面,M INRES算法的运行时间最短,与主流的共轭梯度算法、零空间算法相比M INRES大幅提高了LSSVM模型的求解速度。因此,基于M INRES算法的LW-LSSVM模型是处理高炉铁水硅含量在线预测的理想工具。[Si]预测的数值实验结果如表2所示:

表2 莱钢1号高炉100炉数据预测结果
3 总结
本文首先分别采用M INRES、CG算法、零空间算法和Cholesky分解算法求解了LW-LSSVM模型,并通过基准数据集上的数值实验对比了4种算法的计算性能。实验结果表明 M INRES算法的运算时间短、数值稳定性好,是求解LW-LSSVM模型的理想算法。随后,应用基于M INRES的LW-LSSVM 建立了[Si]在线预测模型,应用案例表明LW-LSSVM模型能自适应的调整模型,具有更高的预报精度,是处理在线预测问题的理想工具。需要指出的是局部加权因子是LW-LSSVM模型的关键因素之一,其设定将直接影响模型性能,而目前局部加权因子的设定仍处于探索阶段,局部加权因子的设定是今后需要重点研究的问题。
[1] Vapnik V N. The Nature of Statistical Learning Theory[C].New York: Springer, 1995.
[2] Suykens J A K, Van T Gestel, De J Brabanter, De B Moor, and Vanderwalle J. Least squares support vector machines[C].World Scientific, 2002.
[3] 郜传厚, 渐令, 陈积明, 孙优贤.复杂高炉炼铁过程的数据驱动建模及预测算法《自动化学报》[J].2009; 35(6) : 725-730.
[4] Radhakrishnan V R, Mohamed A R. Neural networks for the identification and control of blast furnace hot metal quality, [J] Journal of Process Control.2000, 10(6): 509-524.
[5] Saxen H, Pettersson F. Nonlinear prediction of the hot metal silicon content in the blast furnace,ISIJ International[C], 2007;47(12): 1732-1737.
[6] Martin R D, Obeso F, Mochon J, Barea R, Jimenez J. Hot metal temperature prediction in blast furnace using advanced model based on fuzzy logic tools, [J]Ironmaking and Steelmaking.. 2007; 34(3): 241-247.
[7] 刘学艺, 刘祥官, 王文慧. 贝叶斯网络在高炉铁水硅含量预测中的应用. 钢铁[J]., 2005; 40(3): 17-20.
[8] Bhattacharya T. Prediction of silicon content in blast furnace hot metal using partial least squares (PLS), [J]ISIJ International, 2005; 45(12): 1943-1945.
[9] 渐令, 刘祥官. 支持向量机在铁水硅含量预报中的应用. [J]冶金自动化, 2005; 29(3): 33-36.
[10] 刘毅, 王海清, 李平.用于发酵过程在线建模的自适应局部最小二乘支持向量机回归方法. [J]化工学报, 2008, 59(8): 2052-2057.
[11] 高学金, 孙鑫.局部自适应加权LSSVM 在线建模方法及其在间歇过程中的应用. [J]计算机与应用化学, 2013, 30(7): 754-758.
[12] Suykens J A K and Vandewalle J.Least squares support vector machine classifiers, [J]NeuralProcessing Letters, 1999, 9(3): 293–300.
[13] Chu W, Ong C J, and Keerthi S S. An improved conjugate gradient scheme to the solution of least squares SVM, [J] IEEE Trans. Neural Netw., 2005, 16(2): 498-501.
[14] Caw ley G C, Talbot N L C. Preventing over-fitting during model selection via Bayesian regularization of the hyper parameters. J. [C] Math. Learn. Res.,2007, 8 (5):840-861.
[15] Van der Vorst H A,Iterative Krylov Methods for Large Linear Systems, [M]Cambridge UniversityPress, Cambridge, UK, 2003.
[16] C. L. Blake and C. J. Merz. UCI repository of machine learningdatabases Univeoijktrsity of California. Irvine.
M inimum Residual M ethod to Accelerate the Local Weighted LSSVM and its Application in Industry
Lin Chao1, Wang Huajie2
(1. Network and Educational Technology Center, China University of Petroleum, Qingdao 266580, China; 2. School of Management Science and Engineering,Shandong University of Finance and Econom ics, Jinan 250014, China)
Local weighted least square support vector machines regression model is a kind of e-learning model, the model needs constantly retraining according to the adjustment of the training sample. The stable and efficient learning algorithm is the key to the successful application of LW-LSSVM model. This paper utilized m inimum residual method (M INRE), conjugate gradient (CG), null space method and Cholesky decomposition algorithm respectively to solve WL-LSSVM model. The numerical experiment of benchmark database indicates that the computing time of m inimum residual method is the m inimum as well as good numerical stability. A fterwards WL-LSSVM based on M INRES is used to establish the e-learning prediction model of the silicon content in hot metal. The simulation experiment shows that compared w ith LSSVM, LW-LSSVM has higher prediction precision and adaptability.
LSSVM; Local Weighted; M INRE; Silicon Content
TP18
A
2014.09.10)
国家自然科学基金(No. 11326203 );山东省自然科学基金(No. ZR2013FQ034)
林 超(1977-),男,山东栖霞人,中国石油大学(华东),网络及教育技术中心,工程师,硕士,研究方向:计算机技术,青岛,266580
王华杰(1981-),男,山东烟台人,山东财经大学管理科学与工程学院,讲师,硕士,研究方向:管理科学与工程,济南,250014
1007-757X (2014)11-0008-04
