一种基于DSP的电力系统同步采样方法的研究

梁 艳，王昆凡,阚加荣

(盐城工学院 电气工程学院，江苏 盐城 224051)

一种基于DSP的电力系统同步采样方法的研究

梁 艳，王昆凡,阚加荣

(盐城工学院 电气工程学院，江苏 盐城 224051)

为了能够检测出电力系统中的谐波信息并能实时的调整采样频率使之与电网频率的同步，提出一种通过采样数据计算电网电压实际频率的方法，能够动态的调整采样频率，实现同步采样；经过基于DSP的实验验证，能够有效地减少因非同步采样造成频谱泄露的影响。算法具有实现简单、精度较高的优点。

电力谐波；同步采样；DSP；频谱泄露

随着电力电子技术飞速发展和广泛应用，大量非线性的电力设备被应用到电网中。非线性负载的存在使得电网中的电压(或电流)产生畸变，增加系统中的无功损耗，降低了公用电网中电能的使用和传输效率。为了保证电力系统的安全与可靠运行，对电力谐波的控制和治理就显得尤为重要[1]。

目前信号的测量和分析中最常用的是FFT算法[2,3-6]。为了实现信号的测量与分析，需要对其采样，当采样频率与实际频率不同步时，就会产生频谱的泄露，通过FFT计算得到的谐波信息就不准确，无法满足要求。为了减少泄露现象，经常采用各种窗函数和插值法[7]处理，然而效果并不理想。因为基于加窗插值的FFT虽然可以减少频谱泄露和谐波间的互相干扰，但当谐波的含量比较接近时，该方法处理效果不佳，需要增加窗函数的宽度来提高频谱分析的分辨率。

造成频谱泄露的根本原因是由于采样的不同步造成的[8]，通过实时的调整使得采样频率与实际信号频率同步是解决问题的有效方法之一[9]。本文介绍了一种软件同步算法，通过调整采样频率降低频谱泄露造成的影响。通过基于DSPTMS320F28335对整流电流的谐波分析，表明本方法对于频率变化较为缓慢的电力系统有较高的精度。

1 非同步采样频谱泄露分析

为了分析方便，设任意频率的简谐信号，其式如下：

(1)

式中：A0是幅值，f0为频率，φ0为初始相位。

简谐信号经过采样并矩形窗截断后得到的序列为

x(n)=x(nTs)wr(n)=A0sin(2πf0nTs+φ0)

(2)

式中：Ts为采样周期，wr(n)为矩形窗函数，N为采样数，对序列x(n)做离散时间傅里叶变换，其频域值为

(3)

其中：wr(n)的DTFT为

对式(3)在数字频域以2π/N为间隔进行抽样时，可得x(n)的DFT值，其中简谐信号模拟频率f0对应数字频率(k+σ)·2π/N,其中k为正整数，0≤δ≤1，则

(4)

当σ=0或σ=0.7时，x(n)的DFT幅频特性如图1所示。

图1 同步采样与非同步采样后离散频谱的对比Fig.1 Comparison of synchronous sampling with asynchronous sampling discrete spectrum

简谐信号的理想频谱为单位冲激。当如图1a所示同步采样时，各离散点上的DFT谱值与理想信号完全一致；当如图1b所示非同步采样时，离散点上的DFT谱值与理想信号有偏移，同时由于栅栏效应其对相邻谐波也产生了泄漏。因此必须实时调整采样频率使得采样频率与实际信号频率同步，减少因采样不同步造成的短范围泄漏和长范围的频谱旁瓣相互干扰。

2 同步采样的原理与实现方法

同步采样是指被测信号周期T0与采样周期Ts满足关系式T0=TsN(即fs=f0N)的采样方法，其中N为一个周期内采样的点数，fs为采样频率，f0为实际信号频率。

为了减小同步误差可采用不同的方法，主要有：(1)修正采样序列；(2)硬件同步法；(3)准同步算法。

这几种方法存在的问题为：(1)修正采样序列只是将得到的序列进行泰勒级数展开，忽略了高阶系数，并没有从根本上解决采样不同步的问题；(2)硬件同步法是通过数字锁相环得到实际信号的频率，但是其硬件电路抗干扰性、波形的整形均不能得到满意的效果；(3)准同步算法[10]是1984年东南大学戴先中教授提出的一种算法，实际上准同步算法也是一种窗函数。

针对造成频谱泄露的根本原因——采样不同步，通过软件算法先估算出实际信号的频率，并以此调整采样频率实现自适应频率调整，从而减少频谱泄露，提高检测精度。

根据实际电力系统在相邻周期频率变换较慢的特点，采用软件采样自适应算法能很好的减少同步误差。方法如下：

(1)设电网频率为50 Hz，一个周期采样点为N=64，采样频率fs=3 200 Hz，初始采样值为零。

(2)经采样得到第一个周期初始大于零的值设为R[1]，则经过i次采样得到第i个周期初始大于零的值为R[i]。若R[1]=R[i]，且i=N，则实际的频率与设定的频率相同;若R[1]≠R[i]或i≠N，说明实际信号的频率发生了变动。

(3)根据采样值和采样时间间隔，利用偏差值调整采样频率。R[1]为第一个周期大于零的采样值，R[i]为第i个周期大于零的采样值，计算偏差值△的数学模型如图2所示。

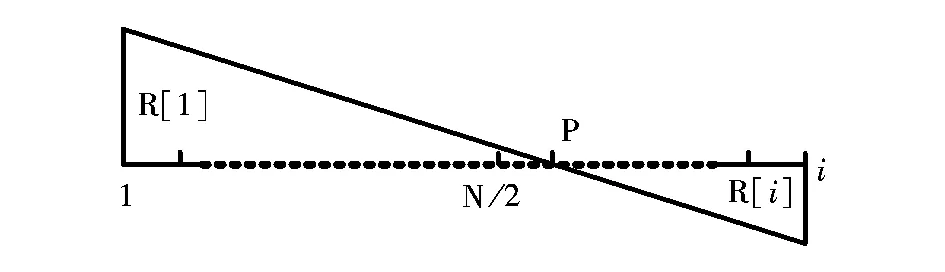
图2 求偏差值的数学模型Fig.2 Mathematical models for seeking deviation

由上图可知P点的值为

(5)

其中l=iTs。

则采样频率与实际频率的总误差

(6)

需要调节的采样误差为

(7)

其中，当△>0时表示实际信号频率变小，反之变大。

采样频率的值为

(8)

在实际采样中如果只采用R[1]和R[i]来计算实际频率，可能会有较大的误差，由于干扰或者某些因数的影响，有时会出现错误。为了解决这个问题，可采用一组R[1]和R[i]附近数据的平均值代替R[1]和R[i]来减少因为个别数据的误差造成的影响，例如取0～5这6个点的平均值代替R[1]的值，取i到i+5这6点的平均值代替R[i]的值，可以有效的减少计算误差。

另外，当对电网电流谐波测量时，如果电网在相邻的周期内发生大幅度的变动(如突加负载、浪涌电流等)，即使这时电流的频率没有发生变化，但是由于相邻两周期采样值有很大的差值，而采样频率的调节又依赖相邻两周期的采样值，这使得采样频率与实际信号不同步而造成谐波信息的测量有较大的误差。

(4)利用FFT运算分析N点信息，并输出波形中的频谱信息。FFT算法的核心是蝶形单元的运算，设其中第m级蝶形单元的信号流程图如图3所示。

图3 时间抽取FFT算法蝶形单元的信号流程图Fig.3 Signal flow of FFT algorithm butterfly unit by time decimation

图3的数学表示为

(9)

其中

(10)

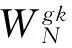
(5)将(3)得到的采样频率作为下一个周期采样基准值，返回第(2)步。

3 系统结构及实现方法

3.1 主电路图结构

本系统由降压变压器、电力二极管、电容及负载连接组合而成，如图4所示。变压器原边接电网，副边输出做不可控整流桥的输入，C为滤波电容，R为电阻负载。

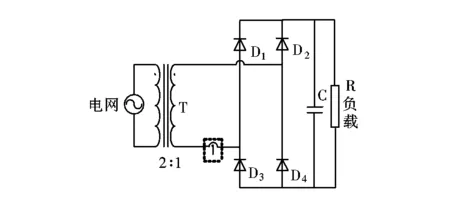
图4 系统主电路结构图Fig.4 The system structure of main circuit

3.2 信号检测电路

图4虚线框中的检测电路框图如图5所示。

检测电路中电流互感器工作原理如图6所示。

图5 硬件采样框图Fig.5 Hardware block diagram of the sampling

图6 电流互感器原理图Fig.6 Current transformer schematics

本文使用的电流传感器型号为CSM050LA，其原边匝数可由设计者根据需要缠绕，图中Rl为测量电阻。

设原边匝数为L1、副边匝数为L2，则电流互感器一次侧电流i1与二次侧电流i2之间有下列关系

(11)

ki为原边与副边的匝数比。

U0为被测量电压，它与被测i1的关系如下

(12)

检测电路中信号调理电路如图7所示。

图7 调理电路原理图Fig.7 Condition circuit schematics

如上图所示，Uin=U0为传感器出来的信号，U1为电压跟随器增强了信号的带负载能力，U2、C1、R3、C2组成的滤波器，滤除信号中的干扰信号，R4与R5组成的分压电路分压输入电压

(13)

由式(13)可得到R5的电阻值，U3与U1的功能一样为电压跟随器，R6、R7是将电压抬升1.5 V，因为DSP中只能测量直流量，要确保得到的交流信号正负峰值在DSP的测量范围。U4的作用为电压串联负反馈，保证输出电压的稳定不随着负载的变化而变化。D1、D2为钳位电路，使得信号在0～3.3 V之间变动，防止烧坏DSP。

3.3 同步采样编程实现

为了达到实时处理数字信号的目的，DSP芯片须具有程序和数据分开的总线结构、流水线操作功能、单周期完成乘法的硬件乘法器以及一套适合数字信号处理的指令集。在DSP上实现的数字信号处理具有实时性好、处理速度快等优点。本设计是基于TMS320F28335DSP芯片的电力谐波分析。

实验中，初始时设电网频率为50 Hz，采样频率为fs=3 200+△，△=0，程序中设定为定时中断。以采样时间间隔作为DSP定时时间，当发生定时中断后采集当前电压值。

系统初始运行时因无法确定当前采样位置，设一标志位flag作为起始采样的标志。当flag=1时，若不满足条件R[i]<=0，R[i+1]>0，返还主程序等待中断；若满足条件，令R[1]=R[i+1]、i=0，清除标志位flag=0。

当flag=0时，若不满足条件R[i-1]<=0，R[i]>0，返还主程序等待中断；若满足条件则一个周期的采样完成，通过R[1]及R[i]计算实际采样频率与预设采样频率的偏差△，并通过偏差值调整采样频率。当采样数组满时即i=L×N(L为正整数)，对采样得到的序列进行FFT运算，分析其中的谐波信息并显示，将i清零重新开始采样。具体流程图如图8所示。

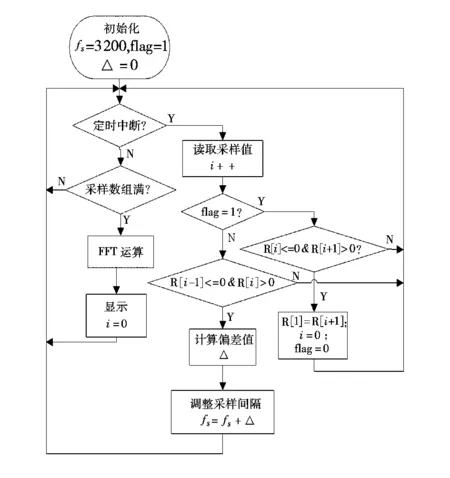
图8 程序流程图Fig.8 Signal process by programming

4 实验结果与分析

为了验证上述理论分析的正确性，制作实验样机进行研究。样机主要有主电路和采样电路两部分组成，主电路由变压器、电力二极管、电容以及白炽灯组成；采样电路由电流传感器、调理电路以及TI公司的TMS320F28335DSP控制芯片组成。

加载程序并运行，在CCS3.3编程窗口点击view->Graph->Time/Frequency，配置相应的设置得到如图9所示波形，为DSP实际采样得到的信号。

图9 DSP采样得到的电流波形Fig.9 Current waveform from DSP sampling

由于调理电路抬升了电压，使得DSP所采集的信号中含有大量的直流(零频谱)分量，而直接进行FFT计算零频谱分量会压制或掩盖附近的小频谱分量，所以在进行FFT计算之前要去除直流分量，去除方法为：首先计算出信号的平均值(即直流量)，并从原始输入信号的所有取样值中减去直流成分。由图9去除直流分量后的波形如图10所示。

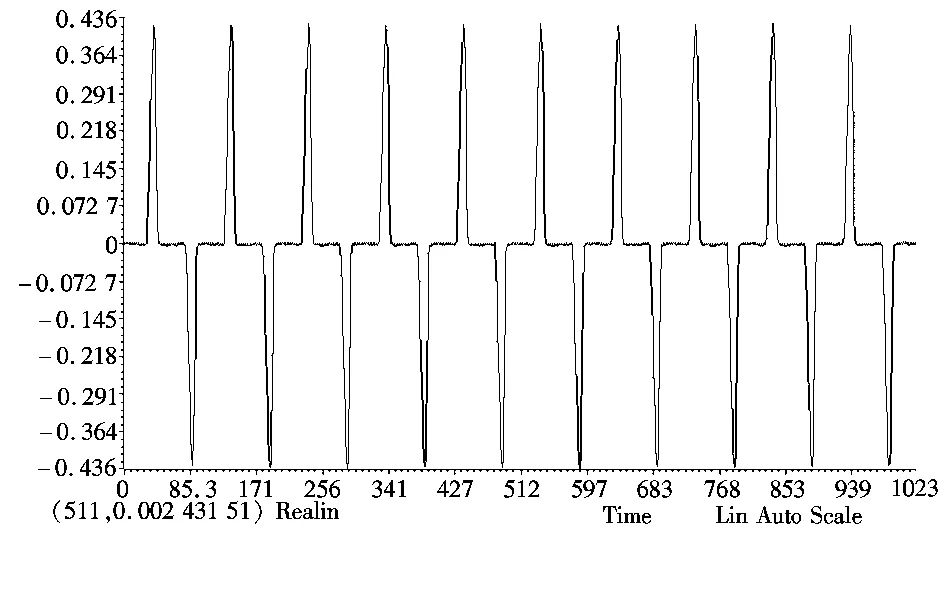
图10 去除直流分量的电流波形Fig.10 Current waveform no DC component

若采样频率与信号频率不同步直接进行FFT运算得到频谱如图11所示。由图11虽然可以分析出序列中含有的谐波次数，但是其中的频谱泄露得比较严重。

图11 非同步采样的频谱图Fig.11 Spectrum by asynchronous sampling

图12为采用上述方法同步采样得到的频谱图。由图可以看出，采用了同步采样可以有效的减少因非同步采样造成的频谱泄露。

为了验证上述得到的频谱图是否准确，图13是功率谐波分析仪检测变压器副边电流波形得到的谐波信息。

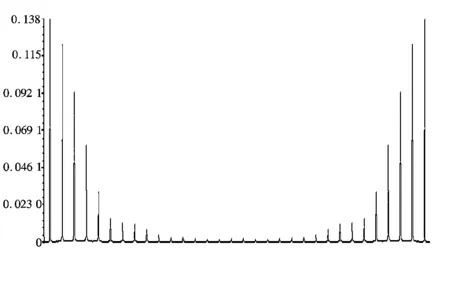
图12 同步采样频谱图Fig.12 Spectrum by synchronous sampling

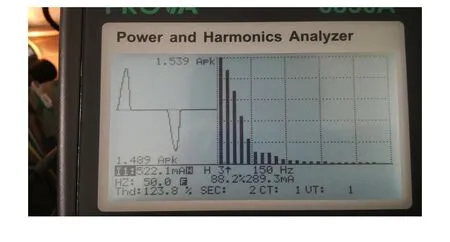
图13 谐波分析仪检测出的谐波含量Fig.13 The harmonic content by harmonic analysis detected

5 结论

本文提出了一种基于DSP的同步采样算法，能实现对实际信号的自适应调节，达到同步采样，较好地抑制频谱泄露的影响，提高谐波检测精度。文中给出了同步采样的硬件和软件设计方法，并通过实验验证，其结果与功率谐波分析仪(型号6830A+6801/6802/3007/3009)分析结果一致，从而证明了本方法的正确性与可行性。该算法实施简单，但当实际信号发生较大变动或者受到较强的干扰时，得到的结果误差较大。

[1] 梅永,王柏林.电力系统信号采集与谐波测量方法[J].电测与仪表，2008,45(9):5-9.

[2] 姚天任.数字信号处理[M].北京：清华大学出版社，2011.

[3] 艾红，邓大伟.TMS320F2812 DSP的FFT运算和DCT实现[J].微型机与应用,2012,30(9):20-23.

[4] 郝小讲，繆志农，黄昆.基于DSP的数字信号处理实验设计[J].实验技术与管理，2012，2(2)：44-47.

[5] 丁洁，张欣.基于DSP的FFT算法在电网谐波检测中的应用[J].中州大学学报，2013,30(1):122-125.

[6] 任先平，陈亮明.基于快速傅里叶变换的电力谐波分析[J].机电工程技术，2013,42(7):70-72.

[7] 马晓春，刘旭东.一种电力谐波分析新算法[J].电工技术学报,2013,33(18):6-8.

[8] 门长有，王荣华，谭年熊.一种用于谐波测量的全数字同步采样算法[J].电力系统自动化，2008,32(22):83-86.

[9] 李晓龙，白连平.电网电压高精度同步采样方法研究[J].北京信息科技大学学报，2012,27(5):81-85.

[10] 戴先中.准同步采样及其在非正弦功率测量中的应用[J].仪器仪表学报，1984，5(4):390-396.

(责任编辑：张英健)

A Synchronous Sampling Method for Power System Based on DSP

LIANG Yan, WANG Kunfan, KAN Jiarong

(School of Electrical Engineering, Yancheng Institute of Technology, Yancheng Jiangsu 224051, China)

In order to detect the power system harmonic information and adjust sampling frequency along with grid frequency in time, this paper presents a real-time computation grid frequency method using sampling datum. This method can realize synchronous sampling through dynamically adjusting sampling frequency. The proposed method is verified by experiment prototype based on DSP. The experimental results show that the method effectively reduce the impact of non-synchronous sampling according to a leaked spectrum, this algorithm is simple and with high precision.

power harmonic; synchronous sampling; DSP; spectral leakage

2014-04-22

梁艳(1974-)，女，江苏盐城人，讲师，硕士，主要研究方向为功率电子变换技术。

TM464;TP30

A

1671-5322(2014)03-0030-06