一种能有效规避威胁区的双层A路径规划算法*
2014-07-24
(1.华中科技大学自动化学院多谱信息处理技术国防科技重点实验室 武汉 430074)
(2.中国运载火箭技术研究院 北京 100076)
一种能有效规避威胁区的双层A路径规划算法*
阳志如1陆宏泽2周成平1
(1.华中科技大学自动化学院多谱信息处理技术国防科技重点实验室 武汉 430074)
(2.中国运载火箭技术研究院 北京 100076)
针对路径规划中A*算法遇到威胁区易陷入局部搜索的问题,对扩展点的估计代价计算方式进行了改进,提出了一种基于A*的双层A*规划算法。在该算法的双层机制中,第一层规划的扩展点估计代价用第二层规划的结果来计算,使得搜索过程中扩展结点的估计代价更接近于真实代价,从而得到该结点更加准确的全代价值,引导算法向更合适的方向扩展,提高了搜索效率。实验表明:在较复杂的规划空间中,该算法能有效解决A*算法遇到威胁区陷入局部搜索的弊病。
A*算法;路径规划;威胁区;双层A*
ClassNumberU666
1 引言
在路径规划问题[1]中,适宜的路径搜索算法在没有人工干预的条件下,能够自动、有效地完成路径规划任务,使运动体能有效地规避威胁、高效地到达目的地。常用的规划算法有A*搜索算法、动态规划法、Dijkstra算法、遗传算法、粒子群算法、数学规划等。所有这些算法中,A*搜索算法由于计算简单、算法易实现,并且在理论上可以保证全局最优解的收敛性,因此得到了广泛的应用。在实际规划任务的约束和需求中,自动和有效地规避威胁区,是A*算法规划的难点之一,它在搜索过程中遇到威胁区易陷入局部搜索问题[3]。
针对A*算法规避威胁区的问题,Khammapun Khantanapoka[4]、Basem M.ElHalawany[5]等提出了基于格网空间的A*规划方法,该类方法能有效威胁建模与裁剪空间,从而更好地规避威胁,但是不能有效结合运动体的运动约束条件;李季[6]、李春华[7]等提出了改进的A*规划算法,该类方法结合飞行器简化运动学方程,更全面地考虑到了飞行器的约束,能有效削减搜索空间,实现自动的威胁回避,但威胁建模只考虑了简单的威胁源的情况,不能解决遇到复杂的威胁区而陷入局部搜索的问题。严江江[8]、刘新[9]等提出了一种导引点集的策略,在威胁区比较密集的地方,用导引点来引导飞行器有效避开威胁区,该方法减小了局部搜索,大大减少了搜索时间,但导引点集的设置没有统一标准,过于依赖人的经验,没有实现自动威胁规避。针对以上情况提出了双层A*规划算法。双层A*的机制是:第一层是标准A*流程,根据代价值引导扩展点去生成子结点;第二层是利用A*的扩展机制,寻找一条从当前子结点到目标点的近似路径,将该路径代价作为该子结点的估计代价。这种计算方式能引导算法更高效地进行扩展。经仿真,证明了算法能有效解决A*算法遇到威胁区陷入局部搜索的弊病,更好地规避威胁。
2 A*算法的基本原理
A*算法是一种典型的启发式图搜索算法[10]。A*算法本身的特性是:在状态空间中进行搜索时,它对每一个搜索的位置利用启发式信息(即代价)进行评估,得到当前最好的位置。每次都选择最好位置进行下一步扩展,直到到达目标(或称找到问题的解),从而省略一些无谓的搜索,提高搜索效率。A*算法能够利用扩展策略,将约束条件、任务需求与搜索过程紧密结合,能在有限的可选状态中,选择最优解,并且在理论上满足全局最优解的收敛性[11]。
2.1 扩展策略
路径规划的研究对象包括飞行器、水面舰艇、地面车辆以及机器人等。考虑一般运动体的约束条件:最小/最大转弯角度、最小/最大转弯半径、最小/最大转弯弧长、距威胁区的安全距离。根据这些约束条件,将A*扩展策略与之紧密结合。同时考虑到最优性和高效性两个特点:最优性指的是扩展策略能够充分覆盖包含最优路径的解空间;高效性指的是扩展策略能够利用约束条件有效裁剪空间,提高搜索效率,降低计算的时空复杂度[12]。基于以上两个特点,结合约束条件来制定扩展策略。图1是扩展策略示意图。
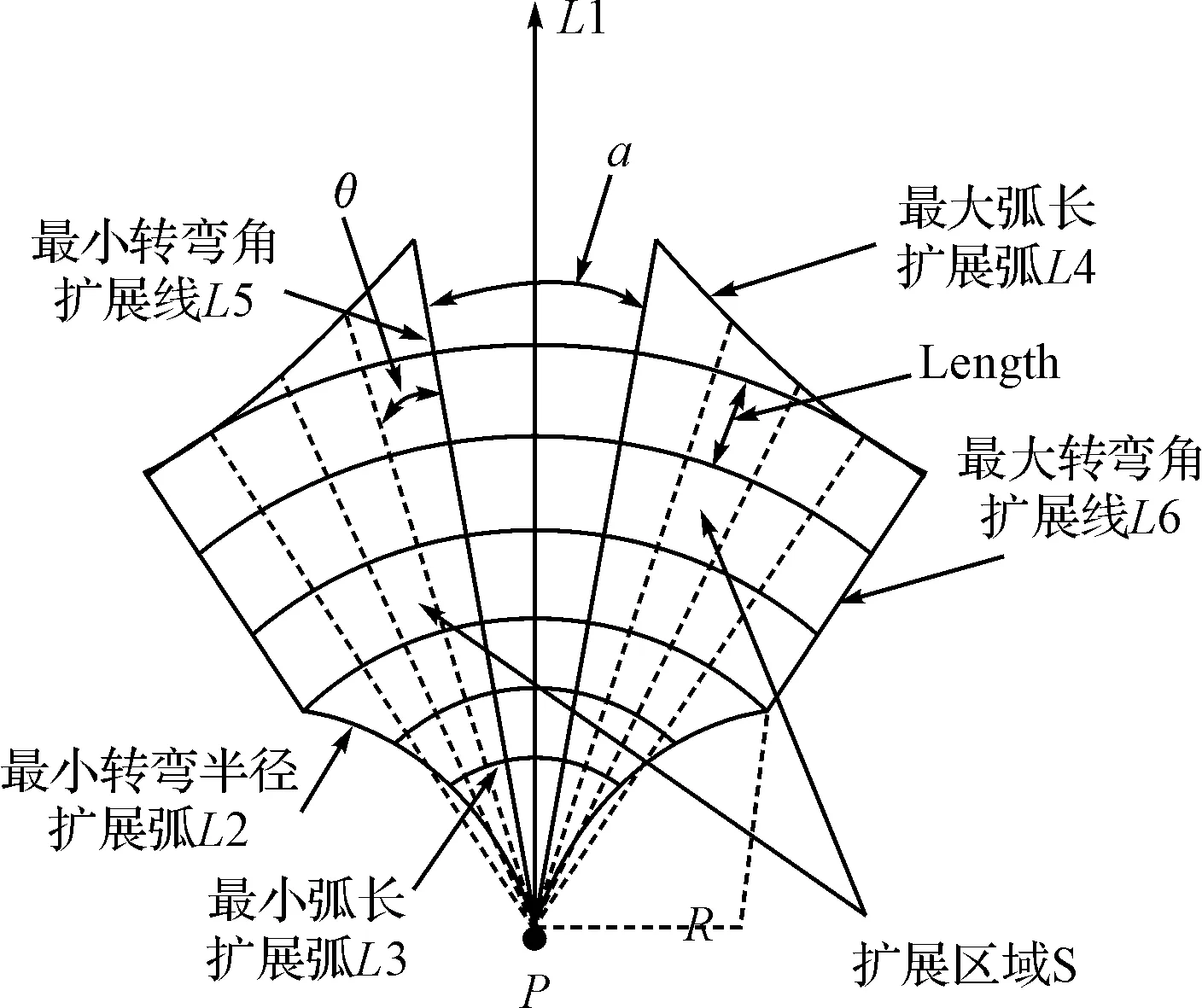
图1 结点扩展示意图
A*的扩展区域S是运动体作一次机动能到达的区域。如图1所示,P是当前扩展点,直线L1代表P点的当前运动方向,显然S是以L1为中心对称。R为运动体最小的转弯半径,L2是沿最小半径机动时的扩展弧线,L3是最小弧长扩展线,L4是最大弧长扩展线,L5是最小转弯角的扩展线,L6是最大转弯角的扩展线。S的近端由最小转弯半径和最小弧长限定,远端由最大弧长限定;左右两边由最大转弯角限定,考虑到最小转弯角а内是不可到达的,则L5将图示а角范围限定在可达区域外。由此可见,扩展区域S是由L1~L6这几条弧或线包络围成的两片对称的区域组成,扩展点是通过网格划分在S中选择点来进行的。
图1中Length为长度步长,θ为角度步长。划分格网时,具体做法是在S内,过P点作偏离L1的角度为K倍θ的一系列直线和以P为圆心作半径为K倍Length长度的一系列圆弧,其中,K为1~n的常数。用所作的直线和圆弧对网格进行划分,把网格交点作为P的扩展子结点。
若M为当前点P的坐标点扩展子结点,则其坐标值与运动方向MFly的计算公式如下所示:
(1)
MFly=PFly+2ξ
(2)
其中L为MP连线的距离,ξ为MP连线与L1的夹角,逆时针为正,顺时针为负。
2.2 路径评价与扩展基本流程
路径规划本质上是最优路线问题,以f(n)表示从出发点V到目标点T的路径上的代价值,则路径规划问题为找到V到T的路径,使代价函数最小。
对A*算法来说,其关键在于设计出一个如下形式的合适的启发函数,这个函数即代价函数。
f(n)=g(n)+h(n)
(3)
g(n)是从起始节点到当前节点n的代价,h(n)为从当前节点n到目标点的实际代价。通过比较f(n),选择合适的结点进行扩展[13]。实际情况中,因为从当前节点到目标点的代价无法计算,一般是用估计代价h*(n)代替h(n),则相应的代价为f*(n)。
理论上,为了收敛到全局最优解,必须满足收敛条件[14]:
h*(n)≤h(n)
(4)
在本文中,代价只考虑距离长度,所以式(4)可以具体化为
(5)
其中li为实际的第i段实际的已规划的路径。li的转弯半径为Ri,第i个点的Mi坐标为Mi(MiX,MiY,MiFly)。li是由Mi和M(i+1)组成。
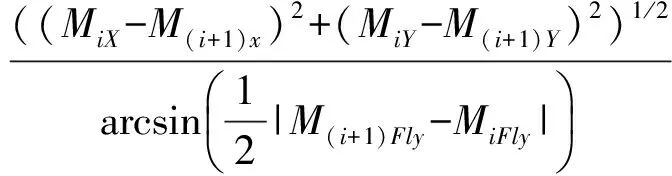
(6)
(7)
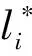
在扩展过程中创建两个表:OPEN表和CLOSE表,OPEN表保存所有已经生成但未被扩展的点,CLOSE表记录已经被扩展的点。
它实现的步聚是:
1)将起点置入OPEN,然后利用扩展策略生成与之相关的子结点;
2)对每一个可行子结点都计算相应的代价f*(n),依次置入OPEN,并选出最小值的点作为新的扩展点,并将其置入CLOSE表;
3)如果该结点是目标点,就结束搜索,转4),否则对新的扩展点进行扩展,并进入步骤2);
4)从目标点回溯记录最短路径,直到出发点。
3 改进的双层机制的A*算法
本文的算法是在二维空间中进行搜索。设(x,y)为规划空间某一点的坐标,则规划空间可以表示为集合{(x,y)|0≤x≤MaxX,0≤y≤MaxY},它代表了一个空间区域。在实际规划过程中,还需要将该空间区域离散化,即将x,y分别按不同的分辨率进行划分,从而得到离散化的规划空间。
结合具体环境,扩展过程中综合考虑的约束条件一般主要有威胁区约束、运动体约束。
3.1 威胁区模型
二维区域的威胁区都具有几何形状,威胁区都是一个二维的几何图形。因此,本文利用多个点组成的多边形来近似建模。这种建模方法虽然一定程度上扩大了威胁区区域,但大大简化了威胁区的表达,能提高效率;另一方面,用多边形建模的方法灵活多变,能表示各种不同的形状信息,使仿真环境更贴近于实际环境,从而提高规划的准确性。
威胁区可以采用的多边形描述为n个点的集合S(P1,P2,…,Pn),Pn表示组成多边形的第n个坐标点,如图2所示,虚线是实际的障碍物模型,用多边形直线进行拟合。
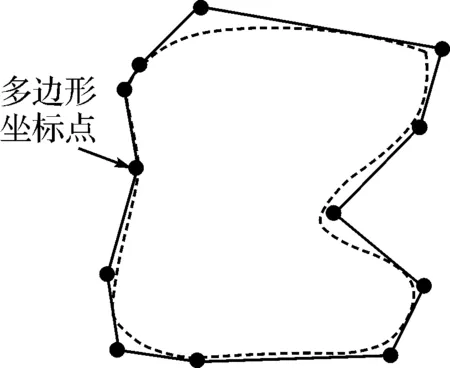
图2 多边形拟合实际的威胁区示意图
由此可见,用这种方法能较好地贴合实际形状,而且,如果坐标点越多的话,越能与实际形状相一致。这种威胁区的建模方法,简单直观,大大简化计算,给规划、编程都带来便利。
3.2 改进思路
在A*规划的规避威胁处理上,要求对所有的威胁均作规避,即要求规划路径满足代价上最优的同时,不能穿越任何威胁区,并将穿越威胁区的点定义为无效点。
为了满足式(4)的全局收敛条件,常规A*的做法是以当前点P到目标点T的直线距离作为启发函数的估计代价项h*(n)。这种做法简单、易于实现,但由于估计代价偏小,导致局部搜索区内(如图3所示)的点被优先扩展,但这些点的子结点又容易落在威胁区内,成为无效点,致使当前路径搜索失败。此情况下,规划极易陷入局部搜索,难以跳出,耗时太大,存在很多的无效点的搜索,搜索效率太低。
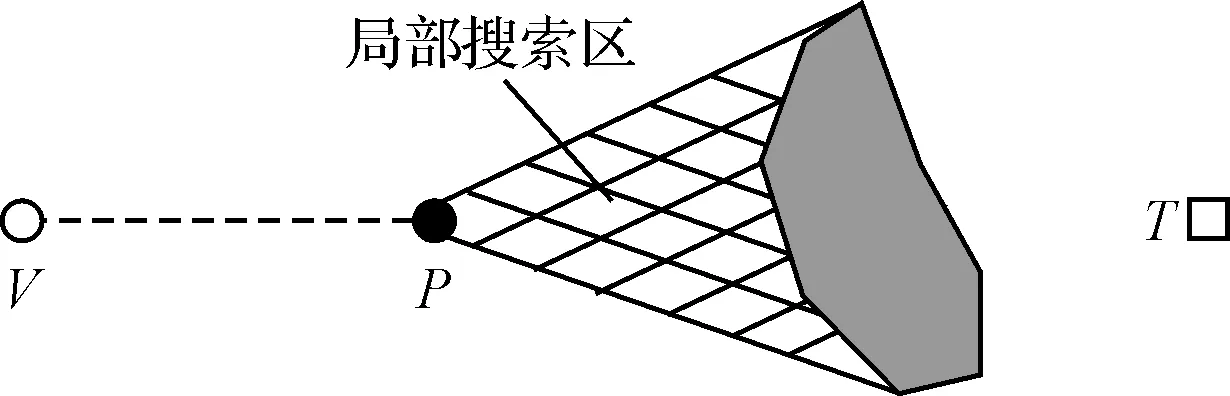
图3 大面积遮挡示意图
为了更有效地利用环境信息,得到扩展点更准确的代价信息,从而避免在一些遮挡面积较大的威胁区前大量无效点的扩展,更快地跳出局部搜索,节省规划时间。在A*算法的基础上进行改进时,必然要对当前扩展点能否通过威胁区作一个判断,把不能通过的点排除在可行点之外;另一方面是要对估计代价的计算方式进行改进。
改进方法是对于第一层扩展点生成的子结点,先判断其能否规避当前威胁区,能规避的点再用第二层A*去计算估计代价值h*(n)。第二层A*的结果是一条由威胁区切点组成的估计路径折线,用这个折线去评估能否规避威胁区,同时,去更准确估算代价。
3.3双层A*规划
判断当前点P能否规避当前威胁区M时,如图4所示,每个威胁区都具有左、右两个可以规避的方向,过P作M的左、右两个切点S、S′,所得切线与PT连线的两个夹角定义为左切角α和右切角β,设置一种机制:给α、β设置一个角度的上限阈值λ,若α或β满足小于或等于λ的条件,则认为当前点P可以通过M的相应方向;否则,认为此方向不可行。两个方向均不可行的扩展点则不能规避当前威胁区。
设置威胁区的角度的上限阈值λ的机制,如图4所示,所有左、右两边切角等于λ点的集合组成的轨迹是两段圆弧,数学意义上,表示ST、S′T弧分别在相应圆上对应的圆周角等于λ。定义两段圆弧与威胁区共同围起来的这个区域为威胁区的局部扩展区。显然,落在局部扩展区内的子结点的切角均大于相应的角度阈值λ。且λ越大局部扩展区越小,大λ对应的局部扩展区包含在相应的小λ的局部扩展区内。
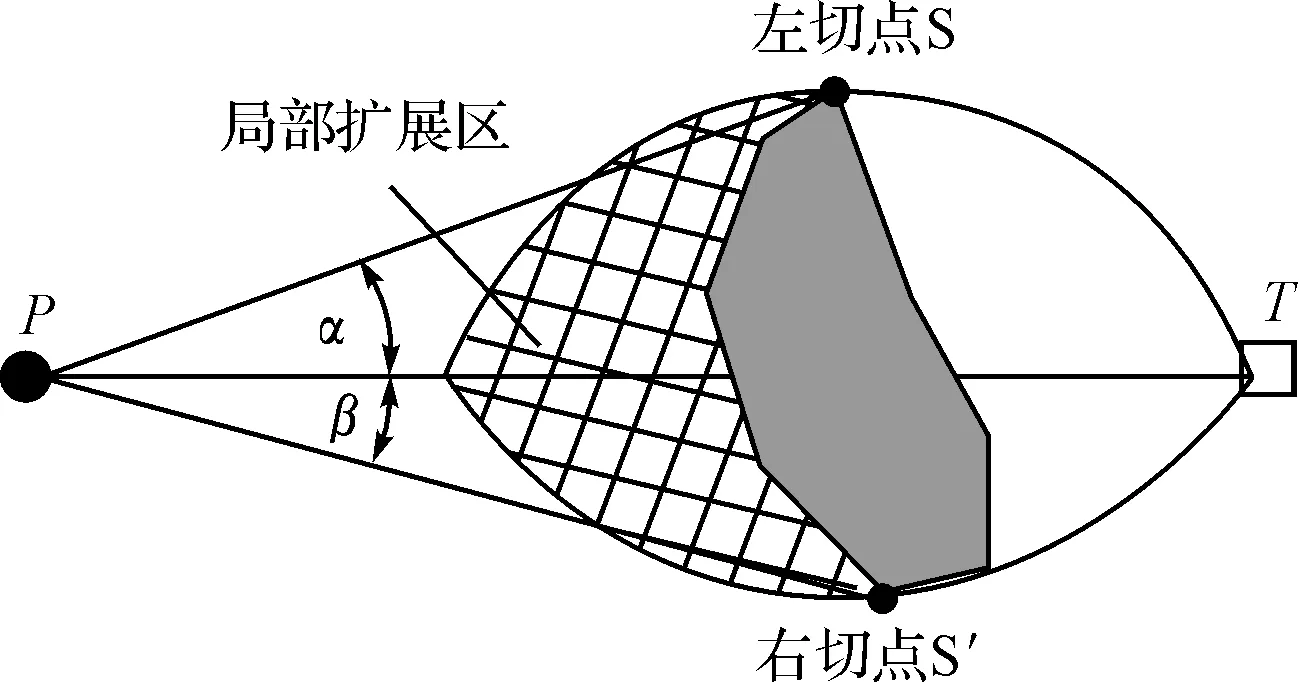
图4 威胁区扩展示意图
这种方法中威胁区的范围有所扩大,人为地把落在局部扩展区的点等效为无效点,把易陷入局部搜索的区域排除在可达区域之外。这样做的优点是:
1)这种方法能避免一些无效扩展,更快地跳出局部搜索,启发的路径能更好地规避威胁区。
2)另一方面这种方法得到的拟合折线在可行性上面是有保障的,不会出现很短的距离作很大拐弯的现象,进一步提高估计代价的准确度。
显然,角度阈值λ的大小决定着局部扩展区的大小。也可以设置λ的不同数值,由此控制局部扩展区的范围的大小,调整扩展和规划速度。λ越小,局部扩展区的范围就越大,可行点的区域就会变小,扩展的速度相对来说会更快。但如果λ过小,导致局部扩展区过大,可行点的选择范围被大大压缩,就会影响路径的全局最优性。λ越大,被排除在可行区域之外的局部扩展区就越小,可行点的范围就越大,路径的全局最优性就更能得到保障。λ的值的范围设置在0°~90°之间,为了更好引导运动体从两边规避威胁区,产生更加平滑的路径,λ不宜超过60°。
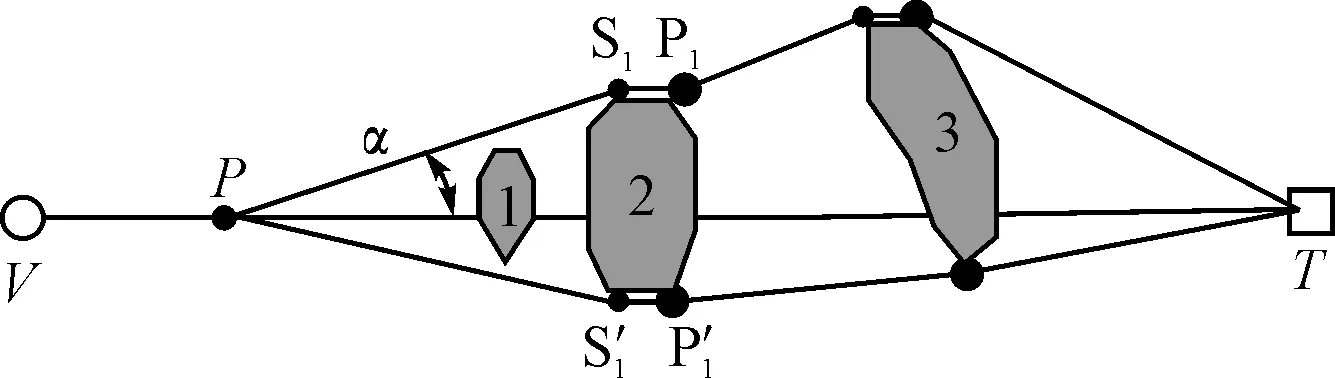
图5 第二层A*示意图
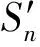
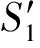
若折线规划到达目标点,且总共有2N个点,则P-S1-P1-S2-P2-…-SN-PN-T即为当前点P的预估折线。利用这条预估折线对当前点P的预估代价进行计算。
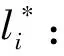
(8)
3.4第二层A*流程
第二层中跟第一层扩展一样,也创建功能相似的两个表:D-OPEN表和D-CLOSE表。
子结点P的第二层A*的过程如下:
1)置P入D-OPEN表中;
2)若D-OPEN表为空,则规划失败;否则从D-OPEN表中取出代价最小的点S;
3)求S到目标点T之间的连线,按顺序记录此连线穿行的威胁区,若没有穿过威胁区,置目标点入D-CLOSE表,规划成功,并转第5)步,否则转下一步;
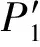
5)规划成功,由目标点回溯,得到当前P点的预估折线路径。
4 实验结果
本算法在CPU为Core E7200 2.53GHz、内存2.0GB的PC机上进行了实验,运行环境为Windows XP,编程环境为VS2005。实验使用了分辨率为30*30、大小为900km×350km的地图和模拟生成的威胁区数据,仿真的基本参数如下:
运动体的转弯角度范围为10°~45°,起始点到目标点的直线距离为740km。其中,扩展的最小半径为100km,最小弧长为70km,最大弧长为250km。角度步长为5°,扩展步长为25km,安全距离为30km。
在同样的环境下,利用两种方法进行路径规划。从方法上比较,常规的A*是以当前点P到目标点T的直线距离作为启发函数的估计代价项,而改进的方法是用第二层A*来计算估计代价,并对角度阈值λ设置不同的数值进行比较。表1给出了以上实验的部分数据。其中,扩展结点的个数是指总共尝试去扩展的节点,有效节点是与无效点相对的概念,是指那些成功加入OPEN表,能组成有效路径的点。
实验参数设置如下:λ=20°,25°,…,45°。实验结果及部分数据如表1、图6、图7所示。
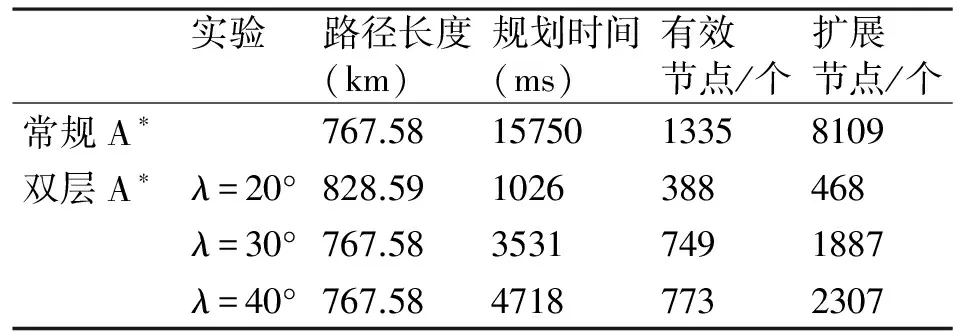
表1 实验数据

图6 常规A*路径的水平投影图
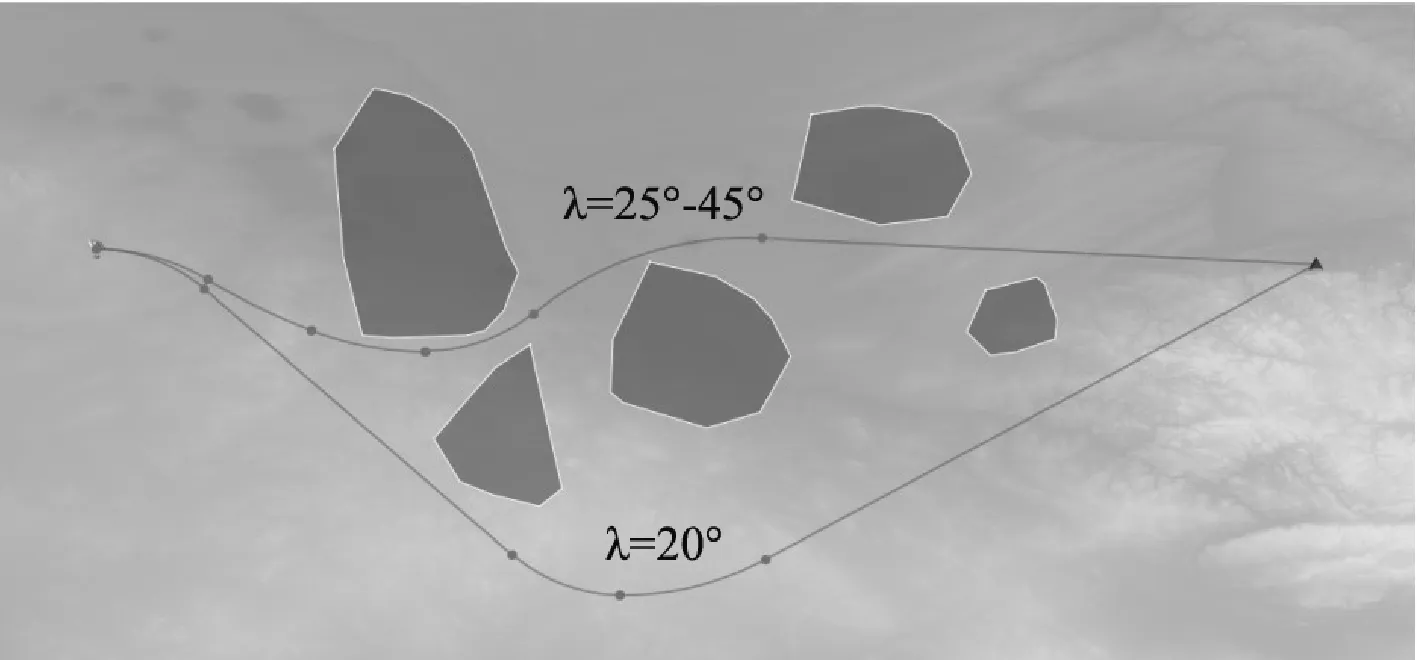
图7 双层A*路径的水平投影图
其中,深色区域表示威胁区,旗帜和三角形分别表示出发点和目标点,灰色圆点表示机动变化点(转弯起始点/转弯结束点)。
从表1数据可知:与常规A*相比,双层A*的规划速度、扩展效率均占有优势。对λ进行调整时,λ过小,时间大大减小,但规划路径效果变差。同样,λ增加到一定程度后收敛到全局最优解,不会再改变规划效果,但会相应增加规划时间。
实验结果表明,改进算法大大减小了无效点的扩展,能有效地提高规划速度、提升扩展点的效率,更好地实现规避威胁区的目的。同时,可以更灵活地通过调整λ的大小的方式来调节规划的速度与规划效果。
5 结语
本文提出了一种双层A*算法路径规划方法,该方法采用双层机制,利用第二层A*对第一层A*的代价进行更准确的计算,从而加快了收敛速度,提高搜索效率。实验结果表明,在满足运动体自身约束、环境约束的条件下,该方法能够有效解决遇到相对较大威胁区陷入局部搜索的弊病。
[1]马仁利,关正西.路径规划的现状与发展综述[J].现代机械,2008(3):22-27.
[2]Chabini, Lan shan.Adaptation of the algorithm for the computation of fastest paths in deterministic discrete-time dynamic networks[J].IEEE Trans on intelligent Transportation Systems,2002,3(1):60-74.
[3]蒙波,皮亦鸣,曹宗杰.基于改进算法的无人机航迹规划[J].计算机仿真,2010(9):29-32.
[4]Khantanapoka K, Chinnasarn K.Path finding of 2D &3D game real-time strategy with depth direction algorithm for multi-layer[C]//2009 Eighth International Symposium on Natural Language Processing,2009:184-188.
[5]Basem M.ElHalawany, Hala M.Abdel-Kader, Adly TagEldeen, et al.Modified Algorithm for Safer Mobile Robot[C]//Navigation, 2013 Proceeding of International Conference on Modelling, Idetification &control(ICMIC),2013:74-78.
[6]李季,孙秀霞.基于改进A-star算法的无人机航迹规划算法研究[J].兵工学报,2008(29):788-792.
[7]李春华,郑昌文,周成平,等.一种三维航迹快速搜索方法[J].宇航学报,2002(3):12-17.
[8]严江江,丁明跃,周成平,等.一种基于可行优先的三维航迹规划方法[J].宇航学报,2009(30):139-144.
[9]刘新,周成平,俞琪,等.基于分层策略的三维航迹快速规划方法[J].宇航学报,2010(11):2524-2529.
[10]Steven M.LaVatle Planning Algorithms[M].London: Cambridge University Press,2006.
[11]杜萍,杨春.飞行器航迹规划算法综述[J].飞行力学,2005(2):10-14.
[12]宋建梅,李侃.基于算法的远程导弹三维航迹规划算法[J].北京理工大学学报,2007(7):613-617.
[13]漆阳华,杨战平,黄清华.A*的改进路径规划[J].信息与电子工程,2009(4):326-329.
[14]Peter E.Hart, Nils J.Nilsson.Bertram Raphael A formal basis for the heuristic determination of minimum cost paths in graphs[J].IEEE Transactions of Systems Science and Cybernetics,1968,SSC-4(2):100-107.
ABi-levelA*PathPlanningAlgorithmforEffectivelyAvoidingtheObstacle-areas
YANG Zhiru1LU Hongze2ZHOU Chengping1
(1.State Key Laboratory for Multi-Spectral Information Processing Technologies,
School of Automation, Huazhong University of Science and Technology, Wuhan 430074)
(2.China Academy of Launch Vehicle Technology, Beijing 100076)
In the case that path A*planning algorithm falling into local search problems in search process when encountering threat areas, the estimated-cost calculation method of the expansion point is improved and a bi-level planning algorithm based on original A*algorithm is proposed.In the bi-level mechanism, the estimated-cost of the expansion node in the first-level is calculated by the outcome of the second-level to make the estimated-cost of search process closer to real cost so to obtain more accurate whole-cost of the current node, thereby guiding expansion of the algorithm to a more appropriate direction, and to improve the search efficiency.Experiments show that in the planning space containing complex threat areas, the algorithm can effectively solve the algorithm encountering threat area into local search problems.
A*algorithm, path planning, threat area, bi-level mechanism
2014年1月3日,
:2014年2月21日
阳志如,男,硕士研究生,研究方向:无人飞行器的航迹规划。陆宏泽,女,博士研究生,工程师。周成平,男,副教授,研究生导师,研究方向:无人飞行器航迹规划。
U666DOI:10.3969/j.issn1672-9730.2014.07.011
