Hamilton体系下海底悬跨管道动力特性分析
2014-07-23刘龙董达善张振
刘龙,董达善,张振
(上海海事大学物流工程学院,上海 201306)
0 引言
海底输油气管道是海上油气田开发生产系统的主要组成部分,是连续地输送大量油气最快捷、最安全和经济可靠的运输方式.[1]受到海底地形地貌、波浪、海流冲刷等影响,海底管道难免出现悬跨,悬跨管道可长达几十米,位于深十几米的海水中.管道悬跨会影响管道的稳定性,易引发涡激共振导致管道疲劳破坏,缩短管线寿命甚至酿成工程事故,造成严重的经济损失和恶劣的社会影响.例如,2000年10月,东海平湖油气田输油管线,因台风和海床冲刷出现多处较长距离的悬跨段,有两处发生管道疲劳断裂,原油生产被迫中断110 d.所以,对悬跨管道进行研究具有重要的理论和工程实际意义.
LARSEN等[2]在悬跨支撑处采用非线性方法处理边界条件,进行海底悬跨管道涡激振动的非线性时域分析.CHOI[3]根据能量平衡理论求解悬跨的固有频率,提出改进的设计准则计算极限管道悬跨长度.MADGA[4]利用二维平面应变有限元模型研究砂质海床上埋置管道的波浪升力,考虑不同土体饱和度对管道升力的影响.杨新华等[5]采用Hermit插值函数对管道动力特性方程进行离散,并以约化速度作为控制条件,确定管道允许悬空长度.包日东等[6]用微分求积法分析不同支承条件下输流管道的允许悬跨长度.李昕等[7]利用水下振动台进行海底悬跨管道动力模型试验,分析管道悬跨长度、悬跨高度、支撑情况和管内运输不同物质等因素对海底悬跨管道动力响应的影响.黄维平等[8]对输送液体的模型管道进行涡激振动试验研究.李晓猛等[9]、郑苏等[10]用实验方法模拟圆截面杆件的风致振动及控制涡激共振的干扰措施.郝志永等[11]用粒子图像测速系统分析和探讨不同列板条纹高度对柱状结构尾涡形态变化的影响.
目前大多数研究基于理想简化模型,对内外流同时作用、材料黏弹性等复杂载荷耦合作用下海底悬跨管道动态特性和疲劳破坏机理的研究还比较少.同时,在方程求解方面,一般采用消元法将方程转换为高阶微分形式,或采用Galerkin法将方程转换为二阶微分方程,然后运用Runge-Kutta法、有限差分法等求解,但这些方法对时间步长都比较敏感,特别是长时间动力响应的精度很难得到保证.因此,有必要探索高效而稳定的数值算法,以更有效地分析海底管道结构的动力学特性.
另外一种思路是将运动方程由Lagrange体系转换到Hamilton体系,在原变量和其对偶变量组成的辛空间中展开求解.例如,STANGL等[12]应用辛变换方法和平均法研究两端支承管道的次谐波共振和组合共振的幅频特性曲线.钟万勰[13]提出精细时程积分法计算结构动力响应,其数值结果可以理解为计算机精确解.该方法已经在结构动力分析、优化控制、偏微分方程求解领域得到广泛应用,具有较好的应用前景.
本文在Hamilton体系下建立海底悬跨管道的对偶正则方程,运用精细积分法分析复杂载荷作用下海底悬跨管道的动态特性,从而为海底管道的稳定性评估和疲劳寿命预测奠定基础.
1 海底悬跨管道运动方程
1.1 一般动力学方程
建立如图1所示模型,管道轴线为x轴,y轴与重力方向相反.根据海底管道特点,假设悬跨段两端为简支支承.
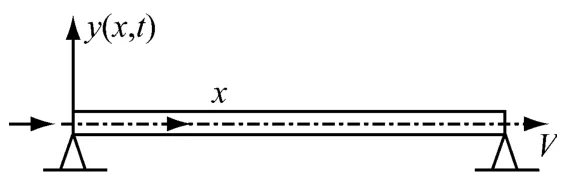
图1 管道悬跨段模型
假设m1和m2分别为单位长度管道及其内流体质量.悬跨管道截面为规则圆形,外径为D,横截面积为S,其悬空长度为L,内流压强为P,轴向力为T.假设:(1)管内流体以恒定流速V流动;(2)海流为稳定流,流速为U;(3)不计管道的顺向和横向振动的耦合作用.
在管道x处取微元dx,将流体微元与管道微元分离进行分析,得到
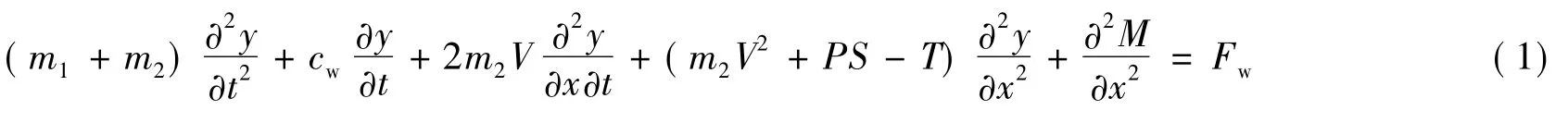
式中:M为弯矩;cw为流体阻尼;Fw为管外流体在单位长度管道上的作用力,主要包括涡激升力和海流拖曳力.涡激升力计算公式为
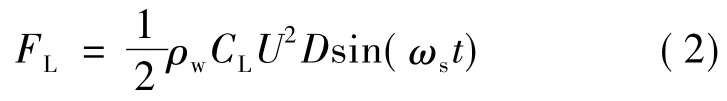
式中:CL为升力因数;ρw为管外流体密度;ωs=为漩涡发放圆频率,Sr为斯特劳哈尔数.海流拖曳力计算公式为
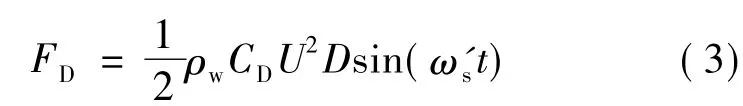
式中:CD为拖曳力因数;ω′s=2ωs为顺向力作用频率.假设管道材料为线弹性材料,本文考虑Kelvin-Voigt黏弹性材料模型,该模型由弹簧与阻尼器并联而成.弯矩可表示为式中:E和η分别为材料弹性模量和黏弹性系数;I为管道横截面的惯性矩.
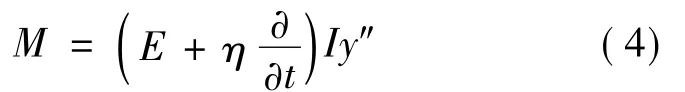
将式(4)代入式(1)中,可得到考虑材料黏弹性的悬跨管道运动微分方程:
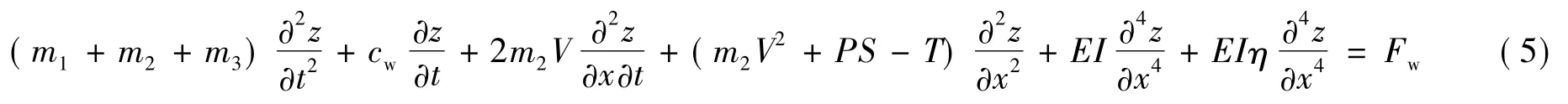
对上述变量进行无量纲化处理:
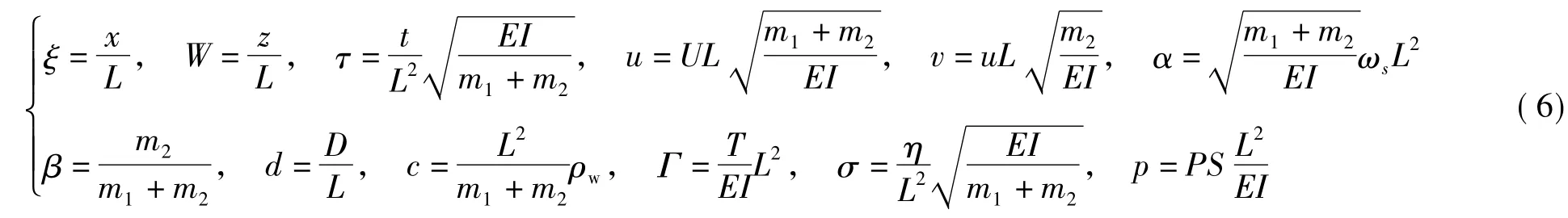
将式(6)代入式(5),得到下列方程:
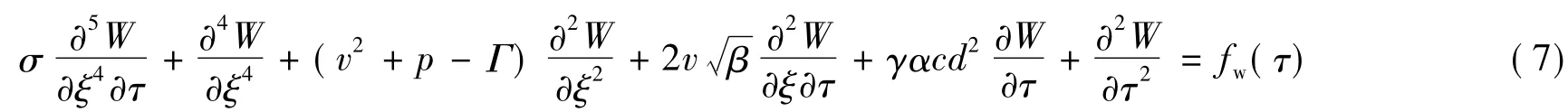
式(7)即为考虑内外流、流体压力、轴向力和材料黏弹性的管道的一般运动方程,下面将其转化为Hamilton体系下的运动方程.
1.2 运动方程辛表述
首先运用Galerkin方法对式(7)进行离散化处理,然后将方程降阶,转化为一阶常微分方程组求解.
假设该方程的解为
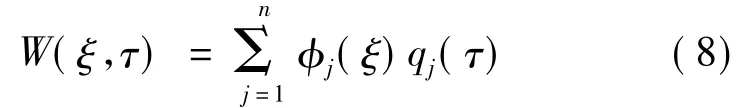
式中:qj(τ)为广义坐标;φj(ξ)为满足边界条件的振型函数.以往研究表明,仅考虑两阶模态即可保证计算结果有足够的精度,故取n=2展开模态计算,运动方程即转化为两阶微分方程.定义以下参数:
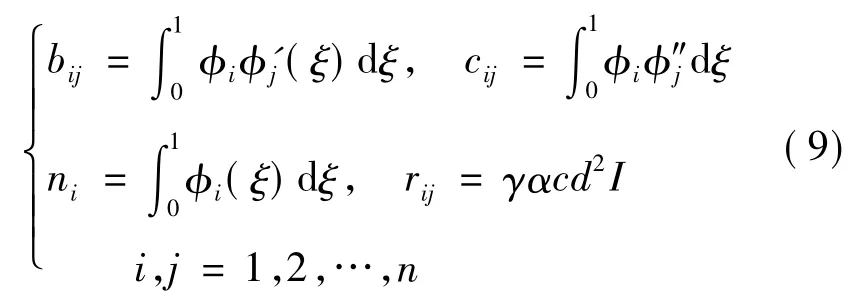
将式(8)与(9)结合后代入式(7),在方程两边同乘以 φi,并在[0,1]上积分,利用特征方程的正交性质化简后,得到
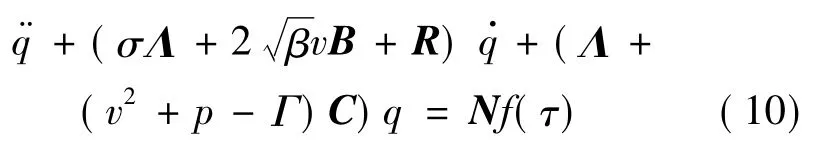
式中:Λ 为特征值矩阵;B,C,N,R 分别为 bij,cij,ni,rij的矩阵.
引入状态向量V=(q p)T,则式(10)可以化为Hamilton体系下的状态向量的微分方程组:

可以看出,悬跨管道方程是典型的非线性动力学问题.下面利用基于线性插值的精细积分法求解.
2 精细积分法
首先根据精细积分法求解齐次方程V·(t)=HV.因为 A是定常矩阵,其通解可写成 V=exp(Ht)·v0,v0为初始值.
精细积分法有2个要点:2N类算法和计算增量.
设数值积分的时间步长为μ.指数矩阵函数的加法定理由下面的恒等式给出:
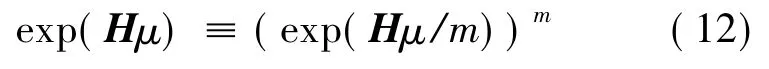
可取m=2N,若N=20,m=1 048 576.由于 μ 本身是不大的时间区段,则τ=μ/m是非常小的一个时间区段.因此,这个极小的时间区段按泰勒级数展开后也有较高精度.这是要点1.
因τ很小,exp(Hτ)幂级数展开5项已足够.此时指数矩阵T(τ)与单位阵In相差不大,故写为
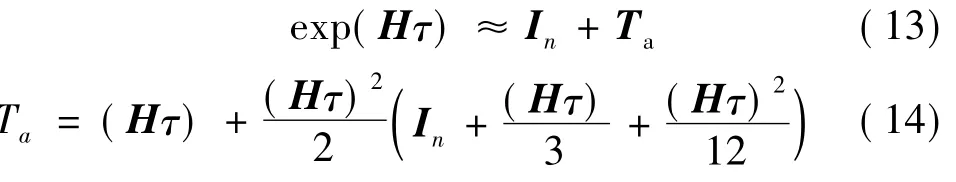
在计算中至关重要的一点是:指数矩阵的存储只能是上式中的增量Ta.因为Ta很小,当它与单位阵In相加时,就会成为其尾数,在计算机的舍入操作中,其精度将丧失殆尽.这是要点2.
根据以上计算步骤编程,即可实现较高的计算精度.
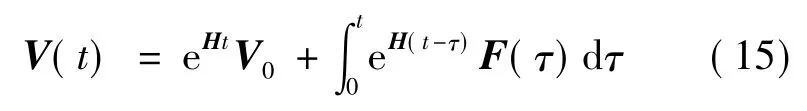
将时间分解为较小的步长,在(tk,tk+1)内的响应可以写为
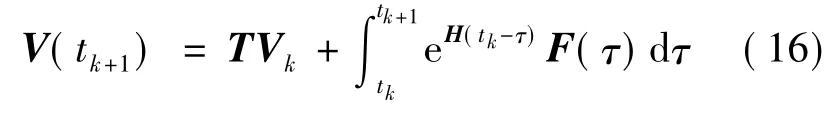
现在的问题集中于如何处理与时间、未知向量相关的F(τ).本文采用高斯公式,即将代入积分项表达式,有
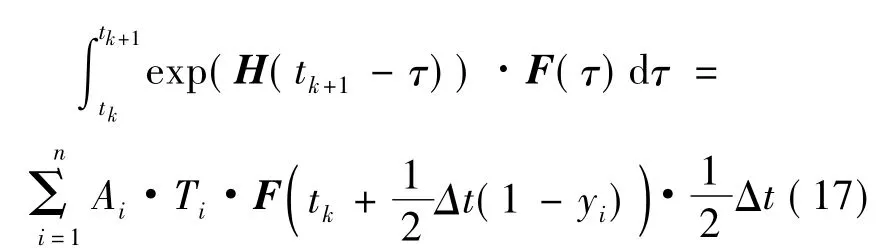
上式中取n=3时为三节点高斯公式,代数精度为5.此时式中参数为:.这样,就得到由当前时刻tk的解求下一时刻tk+1的解的递推公式,从而将精细积分法进一步推广到非线性动力学问题.
3 悬跨管道动态响应分析
影响海底悬跨管道动力特性的因素较多,本文首先计算横向、顺向涡激共振时程响应,并考察海流流速、内流流速、内流压强、轴向力、黏弹性系数对管道振幅的影响.
选择以下管道及流体参数进行计算.管内流体密度为 908.2 kg/m3,管道材料密度7 850 kg/m3,管道材料弹性模量为2.1×1011Pa.管外流体密度为1 025 kg/m3,管道外径 0.426 m,管壁厚 0.014 m,管道跨长 70 m.升力因数 3.0,拖曳力因数 1.2,惯性力系数2.0,斯特劳哈尔数 0.2.此时,不考虑阻尼、轴力、压强等因素,管道第一阶固有频率为0.74 rad/s.
3.1 海流作用下管道振动响应
为计算管道横向共振时的响应问题,令漩涡发放频率等于管道固有频率,计算得此时海流流速为0.266 m/s.计算管道的时程响应,得出管道中点的时程位移响应见图2.同理,计算海流作用下管道顺向共振时程位移响应,见图3.
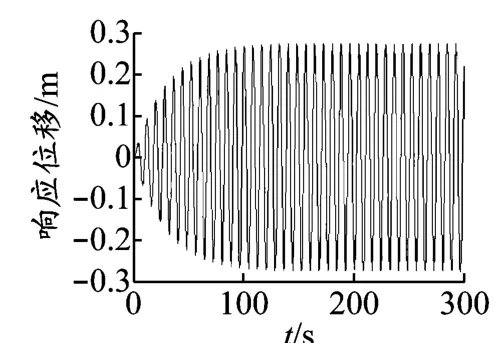
图2 管道横向共振时程响应
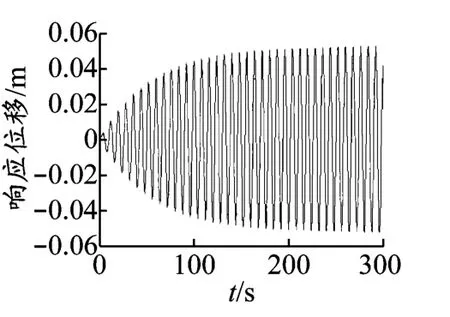
图3 管道顺向共振时程响应
将计算结果与横向振动的时程响应比较可以看出,在涡激振动中管道顺向振动频率是横向振动频率的两倍,但是在200 s时横向共振幅值约为0.3 m,而顺向共振幅值约为0.056 m,不到前者的20%,所以在海流作用下的海底管道动力计算中通常只考虑管道横向振动.
3.2 海流流速对管道振幅的影响
海流流速对管道振幅的影响表现在两方面:一方面海流流速的增加使激励力幅值增大,这使得管道振动幅值增加;另一方面海流流速增加也使漩涡发放频率增加,从而增大水动力阻尼,使得管道振动幅值减小.因此,海流流速对振动幅值的影响相对复杂.图4是海流流速从0到2.0 m/s变化过程中管道振幅的变化.
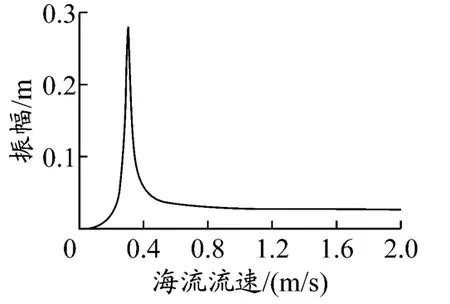
图4 海流流速对管道振幅的影响
从图4可以看出,海流流速的增加引起漩涡频率提升而出现共振.共振时的海流流速为0.266 m/s,这与上节计算所得的共振时海流流速一致.当海流流速大于0.5 m/s时,管道振幅稳定在0.05 m附近,变化较小.
3.3 内流流速对管道振幅影响
一般来说,内流会降低管道的固有频率.取内流流速在0到20 m/s之间变化,并取海流流速分别为 0,0.05,0.10,0.15 和 0.20 m/s 进行计算,得到悬跨段管道垂向振动幅值随内流流速的变化,见图5.从图5可以看出:管道振幅随内流速度增加而增加,特别是在海流涡激发放频率附近,增加更为明显.
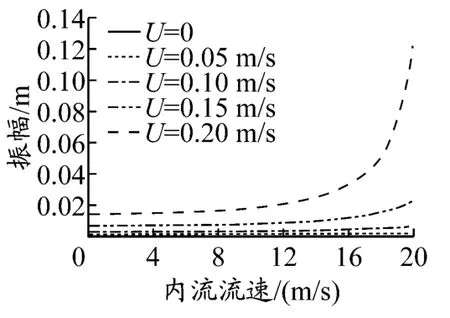
图5 内流流速对管道振幅的影响
3.4 内流压强对管道振幅的影响
选定压强在0到1.5 MPa之间变化,并取海流流速分别为0,0.05,0.10,0.15 和0.20 m/s进行计算,可以得到其对管道振幅的影响,见图6.通过比较可以看出,当外界流速没有达到能引起悬跨段共振的流速时,管道振幅随着内流压强的增加而增加.
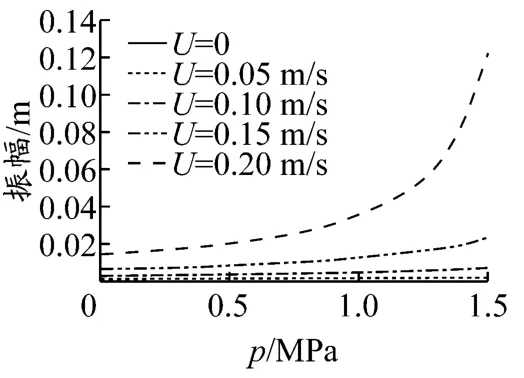
图6 内流压强对管道振幅的影响
3.5 轴向力对管道振幅的影响
以轴向拉力为正,在-150~150 kN之间改变管道轴向力,并取海流流速分别为0,0.05,0.10,0.15和0.20 m/s进行计算,可以得到其对管道振幅的影响,见图7.通过比较可以看出,轴向拉力对管道振幅的影响较小,同时随着轴向压力的增加,管道振幅逐渐变大.
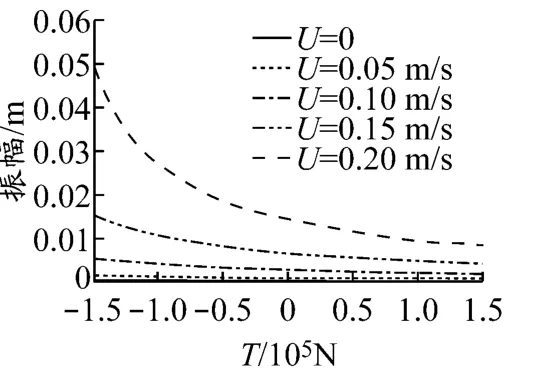
图7 轴向力对管道振幅的影响
3.6 材料黏弹性系数对管道振幅的影响
选择黏弹性系数在0~0.010变化,并取海流流速分别为0,0.05,0.10,0.15 和 0.20 m/s进行计算,可以得到其对管道振幅的影响,见图8.通过比较可以看出,管道振幅随着材料黏弹性系数的增加而减小,但是振幅很小,故材料黏弹性系数对振幅的影响不大.
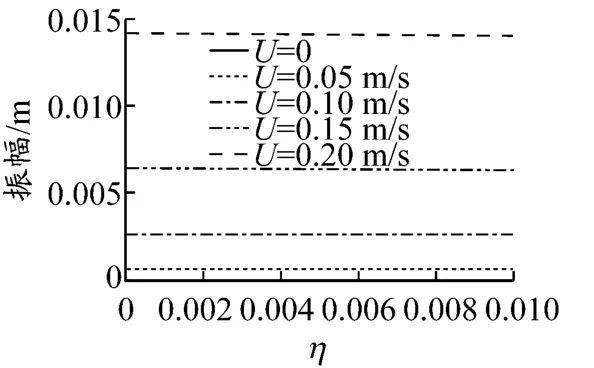
图8 材料黏弹性系数对管道振幅的影响
4 结束语
本文以海底悬跨管道为研究对象,在Hamilton体系下建立复杂载荷环境下悬跨管道动力学方程,应用精细积分法分析载荷参数对悬跨段动态响应的影响.计算结果表明涡激振动中管道主振动为横向振动,振动响应幅值随内流速度、内流压强和轴向压力的增加而增大,而材料黏弹性系数对管道振幅的影响不大.
海底悬跨管道的计算是一个复杂的非线性问题,影响其动力特性的因素较多,因此关于精确计算流固耦合作用下海底悬跨管道的动力特性,对其进行稳定性分析和寿命预测,还需进一步深入研究.
[1]唐友刚.海洋工程结构动力学[M].天津:天津大学出版社,2008:120-131.
[2]LARSEN C M,BAARHOLM G S.Non-linear time domain analysis of vortex induced vibrations for free spanning pipelines[C]//Proc Int Conf Offshore Mech& Arctic Eng.2004:207-215.
[3]CHOI H S.Free spanning analysis of offshore pipelines[J].Ocean Eng,2001,28(10):1325-1338.
[4]MADGA W.Wave-induced uplift force on a submarine pipeline buried in a compressible seabed[J].Ocean Eng,1997,24(6):551-576.
[5]杨新华,郭海燕,娄敏,等.考虑阻尼海底悬跨段管道的动力特性及允许悬空长度[J].海洋工程,2005,23(1):1-5.
[6]包日东,闻邦椿.用微分求积法分析不同支承条件下水下输流管道的动力特性与容许悬跨长度[J].地震工程与工程振动,2009,29(2):131-137.
[7]李昕,刘亚坤,周晶,等.海底悬跨管道动力响应的试验研究和数值模拟[J].工程力学,2003,20(2):21-25.
[8]黄维平,王爱群.海底管道悬跨段流致振动试验研究及涡激力模型修正[J].工程力学,2007,24(12):151-157.
[9]李晓猛,郑苏.引起岸边起重机结构中圆截面杆涡激振动的风速[J].上海海事大学学报,2005,26(2):21-26.
[10]郑苏,钞素莉,唐军领.圆截面杆件涡激振动控制结构实验[J].上海海事大学学报,2006,27(4):14-17.
[11]郝志永,余恒旭,宓为建.柱状结构条纹列板对尾涡形态变化的影响机理[J].上海海事大学学报,2012,33(2):55-60.
[12]STANGL M,BELIAEV N A,BELYAEV A K.Applying Lagrange equations and Hamilton’s principle to vibrations of fluid conveying pipes[C]//Proc 33th Summer School APM.2005:269-275.
[13]钟万勰.应用力学的辛数学方法[M].北京:高等教育出版社,2006:77-91.
