基于Markov机制转换模型的中国拆船市场周期波动
2014-07-23李翀真虹
李翀,真虹,2
(1.上海海事大学交通运输学院,上海 201306;2.上海国际航运研究中心,上海 200082)
0 引言
当今世界各国提倡可持续发展战略,低碳环保成为经济发展中不可忽略的一个重要考虑因素.拆船业作为循环产业的重要组成部分,能提供大量废钢铁以及其他循环利用物资.它的存在有利于航运、钢铁、造船等产业的均衡发展,因此我国拆船业的发展受到国家的重点关注和政策支持.
我国拆船业始于20世纪60年代,改革开放后迅速崛起,经历多次曲折变化成为世界四大拆船国之一.[1]然而随着国际拆船业的持续繁荣,拆船大国之间的竞争越来越激烈.如何促进中国拆船业的发展,提升其国际竞争力成为亟待解决的问题.鉴于此,需要对拆船市场的发展特性有清晰的认识,因此对我国拆船市场波动状态的研究成为重要的研究课题.
针对拆船市场的发展问题,国内外学者从不同角度进行研究.国外学者侧重于研究拆船业产生的生态环境污染问题以及从业人员安全健康问题,对拆船市场发展前景的研究相对较少.NEŞER等[2]对土耳其绿色拆船业进行探究,提出与国际相关法规相协调的环保、安全、健康的可持续发展规划建议.国内学者侧重于研究拆船业的监管制度、法规政策及其对我国拆船业的发展产生的影响.也有业内人士对我国拆船业发展现状进行分析.周鑫等[3]从影响拆船业的因素及中国拆船市场现状出发,对中国拆船业的发展从政府及企业层面上提出相关建议.蒋玉荣等[4]根据中国拆船业的现状给出相关问题的研究对策.王巍巍[5]利用灰色拓扑模型对油船拆船量进行预测.严鹤鸣[6]对中国拆船业的现状进行分析并预测其未来的发展趋势.但是,这些研究多以定性分析为主,并且忽略拆船市场周期波动特征,缺乏全面性.
我国拆船市场具有明显的周期波动特征,但是波动周期不定、波动状态的表现特征不定.在这种情况下用一个统一的模型描述市场已经不能满足研究的需要,因此本文引入Markov机制转换模型(Markov regime-switching model).该模型是 HAMILTON[7]在1989年为研究美国经济周期问题而建立的.此后该模型在经济金融方面的研究中得到广泛应用.国外有很多文献应用Markov机制转换模型进行问题研究,如KIM[8]用异方差的三状态Markov模型研究1926—1986年间美国股市的月收益,GARCIA等[9]应用Markov机制转换模型研究机制转换情况下的真实利率.国内用Markov机制转换模型进行研究的文献比较少.魏巍贤等[10]运用Markov机制转换模型对1987年5月—2006年1月世界原油现货价格的变动进行刻画.王社伟等[11]应用Markov模型的容错系统进行可靠性分析.蒋迪娜[12]应用Markov区制转换模型对波罗的海原油运价在周期性波动过程中的区制转换和持续期依赖特征进行分析.在拆船市场发展分析方面,Markov机制转换模型仍然没有应用先例.
本文建立三状态、无滞后、异方差的Markov机制转换模型对拆船市场的周期波动情况进行分析.根据模型结果可以识别拆船市场周期波动的3种变化机制以及各个机制的平均持续时间,且根据机制转换概率预测未来拆船市场的发展状态.
1 拆船市场Markov机制转换模型的构建
1.1 数据处理
拆船市场周期波动的直观表现是废船拆解量的周期性变化,因此选择我国拆船市场的月拆解量作为原始数据,对一定时期内的拆解量增长率进行分析.根据 Clarkson SIN的数据可以看出1996年1月—2013年8月我国拆船市场月拆解量的变化情况,见图1.从图1可知我国拆船市场的波动情况大体可分为3种机制:机制1下拆船市场收缩,拆解量下降;机制2下市场基本保持平稳,拆解量振荡;机制3下拆船市场扩张,拆解量上涨.3种机制没有固定的变化周期,且波动不对称.
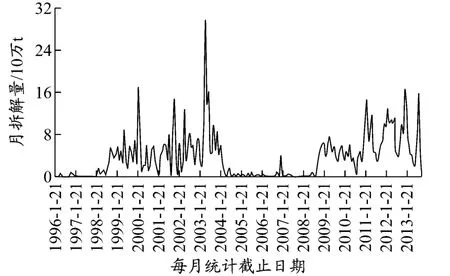
图1 1996年1月—2013年8月我国拆船市场月拆解量变化
通过数据处理,进一步确定建模对象.首先选择月拆解量增长率、季度拆解量增长率、4个月拆解量增长率、半年拆解量增长率进行比较.
(1)选择月拆解量增长率进行分析时,发现真实拆船市场的月拆解量有可能为0,在这种情况下分析月拆解量增长率是没有意义的.因此,令y′i=yi+100,其中yi为i时间的月拆解量,即给月拆解量加上一个极小值(100为所有月拆解量最小值的1/30,远小于各月的拆解量数据),然后对月拆解量增长率的近似值y′i进行分析.对季度拆解量增长率进行分析时作同样的处理.4个月拆解量以及半年拆解量未出现这种情况,因此仍用原数据进行分析.
(2)当时间序列中存在Markov机制转换过程时,使用传统的增广迪基-福勒(Augmented Dickey-Fuller,ADF)检验判断时间序列是否存在单位根非常低效.因此,同时使用ADF检验和Phillips-Perron(PP)检验判断各研究对象的数据平稳性.
(3)采用Akaike信息准则(Akaike Information Criterion,AIC)作为选择模型研究对象的标准之一,选择AIC值较小的数据作为模型研究对象.
通过以上比较,可以得到模型研究对象比较分析表,见表1.比较结果显示,以4个月拆解量增长率作为模型研究对象最佳.

表1 模型研究对象比较分析
我国拆船市场1996年1月—2013年8月每4个月拆解量增长率的变化情况见图2.为简化说明,将52组4个月拆解量增长率数据依次编号,横坐标为数据编号,纵坐标为相应的增长率.使用EViews软件对数据进行分析,根据AIC判断数据滞后阶数,检验结果显示AIC值最小时数据的滞后阶数为0.因此,建立三状态、无滞后的Markov机制转换模型描述我国拆船市场的周期波动特征.

图2 4个月拆解量增长率变化情况
1.2 模型构建
定义状态变量st为t时期的机制状态,st=1,2,3对应一阶三状态Markov过程.一阶Markov过程表示未来状态仅与当前状态有关,与过去所有状态无关.st是不能直接被观测到的,只能通过时间序列的外在表现进行推断.u(st)和σ(st)分别为机制st下单位时间拆解量增长率的均值和标准差,其取值取决于 st.若 st-1=i,st=j,则由机制 i转换到机制 j的概率为.三状态Markov机制转换概率矩阵为

各机制的平均持续时间可以通过下列公式进行推导.不失一般性,假定 n种机制的st满足一阶Markov过程.当前为机制j,那么机制j持续时间T的概率[13]如下:
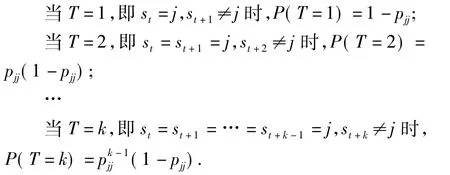
那么,各机制的平均持续时间

1.3 参数估计
采用文献[7]的极大似然估计法对模型参数进行估计.根据文献[14]中给出的推导过程,在εt符合正态分布的假设下,变量yt在st=j时的条件概率密度为

式中:λt-1=(yt-1,…,y0),为从初始时期到 t-1 时期与si对应的所有变量yi(i=0,1,…,t-1)的观察值,即到 t-1时期所能获取的所有信息;α=(u(1),u(2),…,u(k),σ(1),σ(2),…,σ(k))为模型的待估参数向量.

总的对数似然函数见式(5),对数似然函数最大化可得到参数的估计值.得到的st的滤波概率见式(6).平滑概率可以根据文献[8]的平滑方法进行计算.
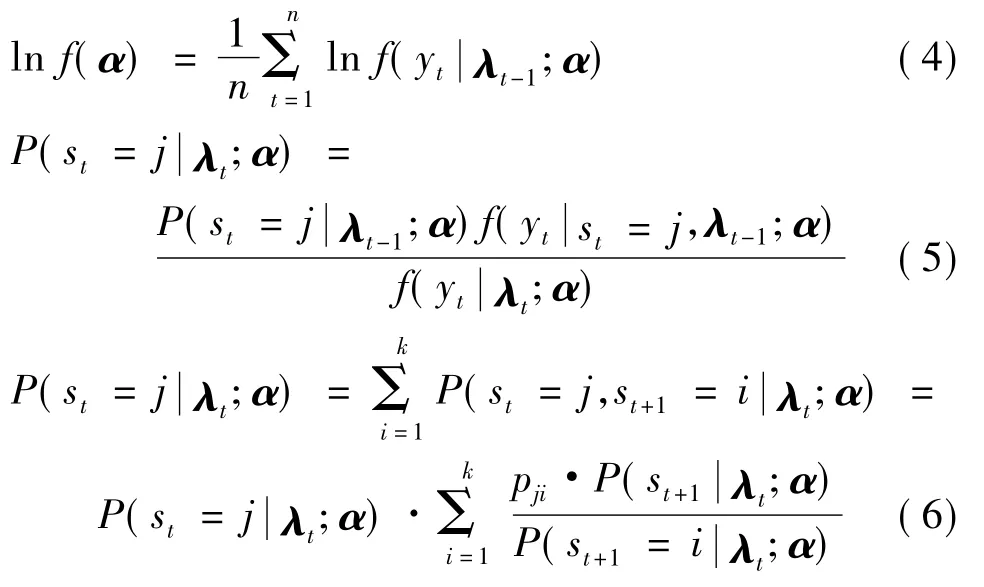
平滑概率是指利用全部的样本信息推断t时期样本处于不同机制的概率.通过该平滑方法可得到Markov机制转换模型的参数估计值.
2 Markov机制转换模型计算结果和分析
2.1 模型参数估计
应用Gauss软件进行编程计算,最终得到Markov机制转换模型的参数估计,结果见表2.表2中:u(1),u(2),u(3)分别表示4个月拆解量增长率在3种机制下的均值;σ(1),σ(2),σ(3)分别表示各均值所对应的标准差.

表2 模型参数估计和检验
模型识别出4个月拆解量增长率波动的3种机制:(1)机制1下4个月拆解量增长率的均值为-0.218 9,标准差为 0.178 1;市场缓慢收缩,拆解量微降,波动较小.(2)机制2下4个月拆解量增长率的平均值为0.961 2,标准差为1.967 9;市场波动幅度很大,处于调整振荡期,但总体仍呈现缓慢扩张的态势.(3)机制3下4个月拆解量增长率的平均值为4.730 4,标准差为19.318 8;市场急速扩张,拆解量迅速增长,市场波动巨大,表现非常不稳定.
通过该模型识别出拆船市场波动机制的表现特点:缓慢下跌、调整振荡、快速上涨.上涨速度是下跌速度的20多倍,远远大于下跌速度,可见我国拆船市场总体表现为急涨慢跌的态势.
根据计算出的Markov机制转换概率矩阵

可以知道拆船市场波动的3种机制会在一定的概率下进行转换.(1)如果市场处于机制1收缩状态,那么下一时期继续保持收缩状态的概率为0.765 4,转换为机制3扩张状态的概率为0.234 6,因此下一时期继续保持收缩状态的可能性较大.(2)如果市场处于机制2振荡状态,那么下一时期转换为收缩状态的概率为0.570 5,继续保持振荡状态的概率为0.429 5,因此下一时期转换为收缩状态的可能性较大.(3)如果市场处于机制3扩张状态,那么下一时期转换为振荡状态的概率为0.823 7,继续保持扩张状态的概率为0.176 3,因此下一时期转换为振荡状态的可能性较大.
各机制的平均持续时间可以通过式(1)计算,又因本文模型数据以4个月的拆解量为研究对象,因此拆船市场各机制下的实际平均持续时间见表3.
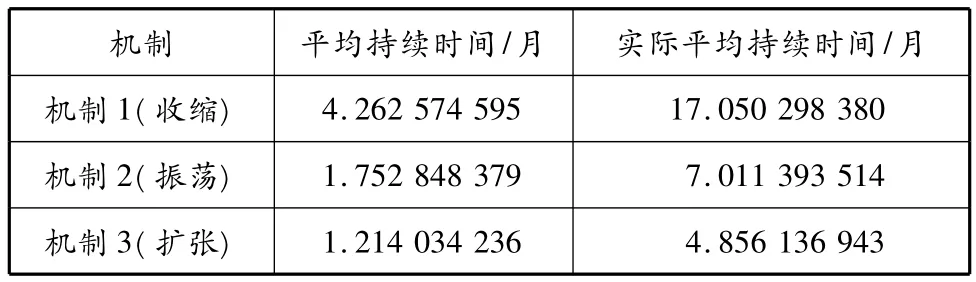
表3 各机制平均持续时间
2.2 平滑概率
根据Guass编程计算结果,得到3种机制的平滑概率,见图3.
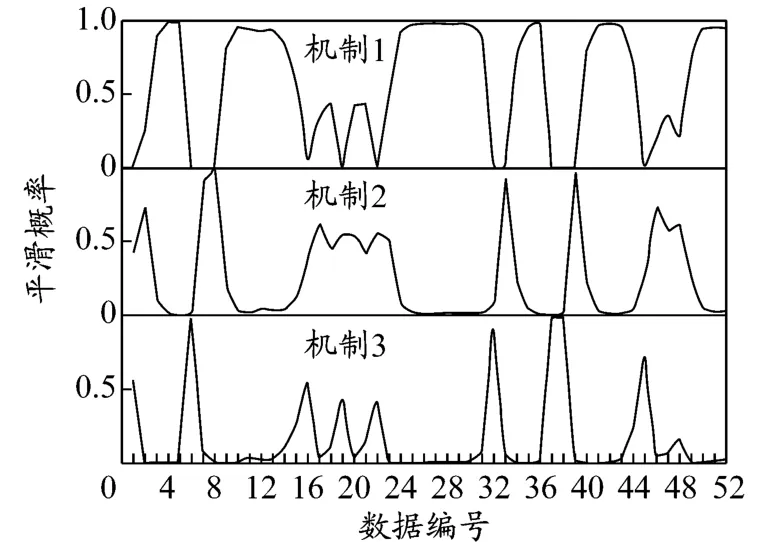
图3 3种机制的平滑概率
平滑概率实际上是一种条件概率,它反映在所有可观测信息集的条件下,所得到的每个时期处于特定状态的概率.通过观察平滑概率图,可清楚地了解每个机制的持续性,以及每个时刻最可能出现的是哪一个机制,基本判断方法是:如果某机制的平滑概率大于0.5,那么在这一时期出现该机制的可能性最大.
根据3种机制的平滑概率图,按照机制转换判断规则,对1996年5月—2013年8月我国拆船市场的波动状态进行划分,并对同期影响市场状态的主要因素进行分析,见表4.

表4 模型计算市场波动状态、真实市场表现及原因分析
3 结论
Markov机制转换模型对我国拆船市场的波动状态有非常好的描述能力.从表4可以发现我国拆船市场周期波动的规律.(1)在周期时间内,我国拆船市场的波动表现为3种机制按照一定顺序进行相互转换.由于本文数据从1996年开始,所以不能判断周期波动的起始机制一定是扩张机制,但是机制交替的顺序是扩张—振荡—收缩.(2)我国拆船市场发展具有周期波动性质,但是市场波动的幅度是不对称的,上涨速度远大于下跌速度,市场总体表现为急涨慢缩的态势.(3)我国拆船市场波动的周期是不确定的.
[1]何剑彤,伍海燕.中国拆船业的发展对策[J].大连海事大学学报:社会科学版,2012,11(1):9-12.
[2]NEŞER G,ÜNSALAN D,TEKˇO GUL N,et al.The shipbreaking industry in Turkey:environmental,safety and health issues[J].J Cleaner Production,2008,16(3):350-358.
[3]周鑫,王立坤.中国拆船业可持续发展的相关建议[J].大连海事大学学报:社会科学版,2007,6(5):53-57.
[4]蒋玉荣,徐张兴,唐玉萍.中国拆船业的现状分析和对策研究[J].中国水运,2009,9(8):83-85.
[5]王巍巍.世界油船拆船量波动与预测研究[D].哈尔滨:哈尔滨工程大学,2011.
[6]严鹤鸣.中国拆船业的现状和发展前景[J].废钢铁,2003(4):16-19.
[7]HAMILTON J D.A new approach to the economic analysis of nonstationary time series and the business cycle[J].Econometrica,1989,57(2):357-384.
[8]KIM C J.Dynamic linear models with Markov-switching[J].J Econometrics,1994,60(1/2):1-22.
[9]GARCIA R,PERRON P.An analysis of the real interest rate under regime shifts[J].Rev Econ & Statistics,1996,78(1):111-125.
[10]魏巍贤,陈智文,王建军.三状态马尔科夫机制转换模型研究——在世界油价波动分析中的应用[J].财经研究,2006,32(6):120-131.
[11]王社伟,陶军,高玉宝.基于马尔科夫模型的容错系统可靠性分析[J].上海海事大学学报,2001,22(3):190-192.
[12]蒋迪娜.基于DDMS模型的BDTI马尔科夫区制转换和持续期依赖特征分析[J].上海海事大学学报,2012,33(1):56-60.
[13]王建军.Markov机制转换模型研究及其在经济周期分析中的应用[D].厦门:厦门大学,2007.
[14]姜婷,周孝华,董耀武.基于Markov机制转换模型的我国股市周期波动状态研究[J].系统工程理论与实践,2013,33(8):1934-1939.
[15]陈曦,徐明,杨立钒,等.谈世界拆船中心转移对中国拆船业的影响[J].船舶物资与市场,2008(1):15-18.
