基于LDA模型的滚动轴承故障类型检测

朱韶平

(湖南财政经济学院，长沙 410205)

1 前言

滚动轴承是旋转机械设备中最精密和最重要的组成部件，在机械设备运行中起着支承和传递载荷的作用，直接影响整台机器的工作性能。但轴承容易因磨损、疲劳和腐蚀等出现裂纹甚至断裂，造成严重事故。对轴承故障及其类型的实时检测可以最大限度地减少或杜绝机械事故的发生，是旋转机械设备故障检测的关键。

随着信号检测和计算机等技术的飞速发展，轴承故障检测方法层出不穷，主要包括频域分析、时域分析、小波变换、专家系统、模糊诊断和神经网络等[1-2]。其中频域分析、时域分析方法在轴承的分布式故障检测中应用效果良好，但对轴承早期故障的检测效果不理想；专家系统存在着知识获取“瓶颈”和不完全性知识表示不足等问题。

基于神经网络和小波变换的轴承故障检测方法弥补了频域分析与时域分析方法只适用于平稳信号分析的缺陷，可以有效地应用于非平稳信号的分析。如文献[3]利用时域分析方法对轴承的运行状况进行粗略判断，但无法确定故障的部位和性质。而文献[4]对滚动轴承的振动信号进行了频谱分析，根据频谱图的结构和故障特征的频率实现了对轴承早期故障的精密诊断。文献[5]根据小波分析多尺度、频窗和时窗宽度可调节等优点对滚动轴承的故障进行检测，弥补了时域分析方法难以监测到突变信号的缺点，取得了良好的检测效果。文献[6]通过小波包算法采用无频带错位的方法精确地提取了滚动轴承的故障特征，并清晰地刻画出了滚动轴承故障冲击的特征函数，具有很高的信噪比。文献[7]采用小波包变换的方法对水泵轴承的振动信号进行分解重构，提取水泵轴承的能量特征及其故障特征，能很好地检测出水泵轴承的故障。文献[8]利用SVM算法提出了基于支持向量机的滚动轴承故障诊断模型；文献[9]将LS_SVM与半监督学习相结合,提出基于SLS_SVM的滚动轴承故障诊断方法；文献[10]将Boosting模糊分类方法引入到滚动轴承的故障诊断中，取得了较好的诊断效果。然而这些方法仍需要较多的人工干预，不能完全实现轴承故障及其类型的全自动检测，且大都是针对剥落等单一故障的检测，对裂纹等产生的早期微弱故障信号研究较少。

为了提高滚动轴承故障检测的准确率，减轻操作人员的劳动强度，结合小波包变换和LDA(Latent Dirichlet Allocation)算法，提出了一种新的基于LDA潜在主题模型的滚动轴承故障类型检测方法。首先利用小波包变换算法对轴承的振动信号进行精细的分解和重构，提取轴承振动信号的能量特征及其所包含的故障信息特征；然后利用“词袋”模型[11]将故障信息特征表示成视觉词向量；最后使用LDA潜在主题模型对轴承故障类型进行精确检测。

2 基于小波包变换的轴承特征提取及其故障特征表示

精确提取轴承的故障特征是轴承故障检测的关键，针对传统轴承故障特征提取方法存在的不足，采用一种新的小波包变换算法提取轴承振动信号的能量特征及其所包含的故障信息特征。

2.1 小波包变换算法的基本原理

小波包变换算法[12-13]是一种将振动信号进行多层次精细划分和分析的多分辨分析方法，基本原理是对振动信号进行小波包分解与重构。首先将振动信号通过多分辨分析方法分解到各个频段，并进一步对没有细分的高频振动信号部分进行分解，然后根据被分析信号的特征，自适应选择与信号频谱相匹配的频段，以提高时频分辨率。

设正交小波基的低通滤波器系数为hk，高通滤波器系数为gk，定义小波包为

(1)

小波包分解是一种改进的小波分解方法，在全部的频带范围内对信号进行正交分解，即对每次分解后的低频信号和高频信号进行再分解，同时提高了低频和高频部分的频率分辨率。小波包分解的层数越多，频域分辨率就越高，但时域分辨率越低。为了使频域和时域的分辨率同时得到提高，采用Mallat算法[14]对小波包进行分解与重构，可以根据不同尺度对已知信号进行多级分解，将信号分割成细节信号和逼近信号。具体步骤为：

(1)在多分辨率分析尺度空间中，分别定义尺度函数和小波函数为

(2)

(3)

(2)小波包分解与重构。设an,j,m为第j层小波包分解的第m个子频带的第n个系数，小波包分解实质是由ak,j+1,m计算an,j,2m和an,j,2m+1，即

(4)

(5)

小波包重构实质是由ak,j,2m和ak,j,2m+1计算an,j+1,m，即

(6)

式中：k为非负整数。原始信号经过j层小波包分解得到2j个小波包。原始信号S经j=3层小波包分解的小波包分解树如图1所示。

图1 3层小波包分解树

2.2 振动信号特征提取及其故障特征表示

对滚动轴承振动信号进行3层小波包分解与重构，提取能量特征；对重构后的信号进行相应的分析，将与故障信息无关的频段信号去掉，进一步提取故障特征信息。

根据滚动轴承常见的磨损、疲劳、腐蚀、压痕、断裂和胶合6种故障，定义6维滚动轴承故障特征向量，并采用“词袋”模型将提取的故障特征表示成视觉词向量。具体算法为:

(1)采用加速度传感器获取滚动轴承的振动加速度信号S。

(2)对采样信号进行3层小波包分解,提取第3层从低频到高频8个子频带的信号特征及对应的小波包分解系数a3i(i=0,1,…,7)。

(4)设xik表示重构信号S3i的离散点的幅值，其中(i=0,1,…,7；k=1,2,…,n)。则各子频带信号的总能量为

(7)

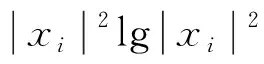
(7)采用“词袋”[11]模型将轴承故障信息特征表示为离散的视觉词vj，通过K均值聚类统计各视觉词个数，得到轴承故障特征的视觉词向量为

d={n(S,v1),n(S,v2),…,n(S,vN)}，

(8)

式中：S为轴承振动信号；n(S,vj)为振动信号中包含故障信息特征视觉词vj的个数。

3 基于LDA模型的轴承故障类型检测

轴承故障检测的实质是：根据提取的特征信息判断轴承工作是否正常，提取工作不正常轴承的故障信息特征，并进一步判断轴承故障属于哪种类型。在此，使用LDA模型实现轴承故障类型的检测。

3.1 LDA模型

LDA模型是一个3层次的Bayes模型[15]，其使用高效variational inference算法估算预测值，并利用EM迭代算法估计Bayes模型中的参数，解决了同义词和多义词的问题，是一种对自然语言进行建模的语言模型，能够预测非训练集中的文档和词的主题分布，在信息检索、文本建模、文本分类、个性化推荐等智能信息处理中得到了广泛的应用[16-20]。

在此，将LDA模型创新性地应用到轴承的故障检测中，将提取的轴承能量特征中包含的丰富故障信息特征转换成视觉词汇直方图来表示训练样本。在训练中，主题通过计算最大化目标函数得到，且故障特征与主题一一对应，能够保证主题的个数和正确性，是一种无监督学习，能有效提高轴承故障类型检测的正确率。

给定训练样本集{d1,d2,…,dj,…，dN}，其中有N个信号、M个故障特征词和k个主题。dj为输入信号，即轴承的运行状态信号；zk为主题；wi为故障信息特征词；α为主题的先验分布参数；β为主题中词的分布参数。dj,zk,wi三者的联合概率结构如图2所示。

图2 LDA潜在主题模型图

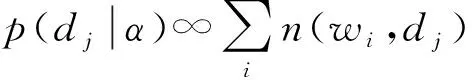
p(wi|zk,β)。

(9)

又因p(wi|zk,β)和p(zk|dj)服从Multinomial分布，通过边缘化主题zk得到条件概率，即

p(wi|zk,β))ddj。

(10)

最大化目标函数为

(11)

利用EM迭代算法最大化目标函数来对参数α和β进行估计。具体步骤如下：

(1)Step-E，求当前估计参数条件下潜在变量zk的后验概率。给定α和β，估计p(zk|dj,wi)，即

α=p(zk|dj)，β=p(wi|zk)，

p(zk|dj,wi)∞p(wi|zk)p(zk|dj)。

(12)

(2)step-M，使用E步计算潜在变量zk的后验概率，估计新的参数值α和β。给定p(zk|dj,wi) 和n(wi,dj)，估计α和β为

(13)

(14)

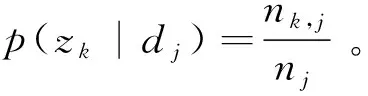
3.2 故障类型检测

给定1个待检测的轴承运行状态信号dt及故障的类型数k，输出为故障类型C。使用已训练的LDA模型对新输入的运行状态信号及其所包含的故障信息进行分类检测，实现轴承故障类型的检测。算法具体步骤为：

(1)利用小波包分解算法提取轴承运行状态信号的能量特征及其包含的故障信息特征。

(2)利用“词袋”模型将故障信息特征表示成视觉词向量d。

(3)采用LDA模型，通过EM算法最大化目标函数估计各主题zk与待测输入信号dt的概率结构p(zk|dt)，即

(4)进行E，M两步迭代直到收敛。

(5)计算轴承故障类型C=argmaxkp(zk|dt)。

4 试验结果与分析

为验证上述算法的有效性，在AMD2.4 GHz处理器和4G内存的测试平台，以及windows XP和VC++6.0的软件环境下，对磨损、疲劳、腐蚀、压痕、断裂和胶合6种常见的轴承故障进行检测。

试验轴承型号为SKF 6205-2RSL,基本尺寸参数为内径25 mm，外径52 mm，宽度15 mm。首先，利用电镀加工技术分别在被测轴承(电动机轴承)的内、外沟道及钢球上设置直径为0.007 mm和0.022 mm的单点故障；通过轴承固定端盖上方的MMAS40G加速度振动传感器采集振动加速度信号；然后将获取的数据进行标准化处理，获取训练样本和测试样本各600个，其中训练样本由经验丰富的工人反复判断，每种故障类型各取100个；最后由LDA模型分别对600个训练样本和600个测试样本(也包含6种故障数据)进行故障检测。

在故障直径0.007 mm，电动机负载3 HP(2.2 kW)，转速1 750 r/min，采样频率12 kHz的工况下进行轴承故障检测，检测结果混淆矩阵如图3所示。

图3 轴承故障检测结果混淆矩阵

由图可知，压痕和断裂的检测精度均为100%，疲劳和腐蚀的检测精度高达98%，磨损和胶合的检测精度低于其他几种。当轴承处于正常运行状态时，由周期性振源引起的响应使振动加速度信号的能量主要集中分布在低频段，当轴承运行发生故障时，会产生一种瞬态激振的脉冲冲击响应，使振动加速度信号的能量主要集中表现在高频段。当轴承出现疲劳、腐蚀、压痕、断裂故障时，高频信号能量激增值大，检测较容易且精度高；而轴承出现磨损和胶合故障时，高频信号能量激增值相对较小，检测精度相对较低。

为进一步验证算法的检测效果与检测精度，在故障直径0.022 mm，电动机负载0，转速1 798 r/min，采样频率12 kHz的工况下，与Boosting及SVM检测算法进行了对比，结果见表1。

表1 不同算法检测结果对比

由表中数据可知，LDA模型总体检测精度为97.5%，优于其他2种算法，完全可以满足实际轴承故障检测的要求。

5 结束语

针对传统滚动轴承故障检测存在的问题，结合小波包变换算法和LDA模型，提出了基于LDA潜在主题模型的轴承故障类型检测方法，克服了人工检测轴承故障存在漏检和误检的缺点，可实现轴承故障及其类型的全自动检测。

小波包变换算法能快速提取轴承振动信号的能量特征及其故障特征，LDA算法则无需用户对训练样本进行标注，降低了训练样本收集的难度，能快速、准确地对轴承的故障及其类型进行检测。试验表明，检测结果与轴承运行状态的一致性较好，精度较高。该方法可以有效监测轴承的运行状态，快速准确地识别轴承故障及其类型。