立足课程标准化解传统与创新的矛盾——《直线与平面垂直的判定》一课中的行动研究法

王丽媛

（延边第二中学，吉林 延吉 133000）

一、研究问题 制订计划

所谓“行动研究法”，是指由社会情境(教育情境)的参与者为提高对所从事的社会或教育实践的理性认识，为加深对实践活动及其依赖的背景的理解所进行的反思研究。

“计划”是行动研究的第一个环节，它始于解决问题的需要和设想。本节课主要内容是直线与平面垂直的定义、判定定理的探究学习及定理的简单应用，课标要求，通过对空间点、直线、平面位置关系的教学，进一步提高学生的空间想象能力，发展推理能力，感悟和体验“空间问题转化为平面问题”、“线面垂直转化为线线垂直”、“无限转化为有限”等数学思想。

本节课的内容在立体几何的学习中处于非常重要的地位，在之前也有很多优秀的课例，比较老教材的特点，课标的要求遵循“直观感知-操作确认-归纳总结-初步运用”的认知规律，重定理的探索过程，轻证明。因此，从“以学论教”的角度讲，摆在教师面前的问题是如何在学生已有认知的基础上，形成一个学生能够独立探究的环境，锻炼学生的动手、动脑探究的能力，使学生学会、会学，进而乐学。

二、把握方法 “互动”“统一”

行动计划的执行和实施是具有灵活性的。苏霍姆林斯基认为，在人们的心灵深处都有一种根深蒂固的需要，那就是希望感到自己是一个发现者，研究者。在本节课的实践过程中，始终贯彻“双互动、四统一”的教学范式，不断修正实践与预想的差距，力求使学生感受到未知转变为已知的完整过程，体验探索的乐趣。

(一）关于直线与平面垂直概念的教学

直线与平面垂直是空间中线线垂直的延续，是面面垂直的基础，是空间中垂直位置关系间转化的重心。在线面垂直概念的教学环节中，教师先结合战士站军姿、照片里的石柱与它在地面上的影子垂直等实例，引导学生直观感知线面垂直关系，继而提出问题：怎样给直线与平面垂直下个定义？鼓励学生用规范的数学语言概括出直线与平面垂直的定义。教师设计的问题要简洁、明确、层层递进，有效地推进学生思维的生成。为此，设计问题如下：

1.石柱所在直线与影子的位置关系？与地面上其它直线的位置关系？理论基础是什么？

2.将教科书直立于桌面，书脊所在直线与桌面上的直线的位置关系？

教师用语言引导，完成概念的生成过程。

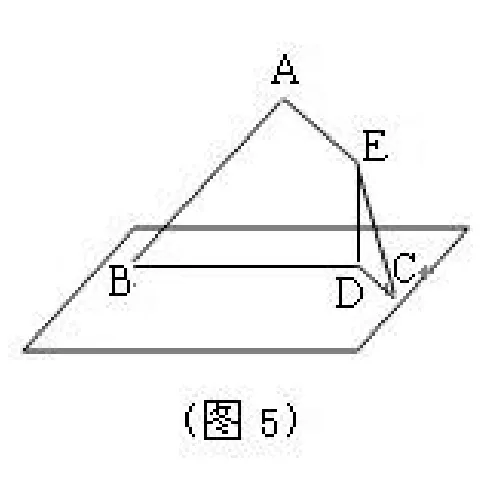
这个核心概念的形成主要依靠的是学生对感性材料的抽象概括。概括是形成和掌握概念的直接前提。在概念生成之后，笔者将下图用 PPT展示给学生，引导学生直观体会概念的核心词“任意”的意义，并与“所有”“无数”辨析学习。提供反例可以帮助学生消除概念认识上的偏差。

（另外，本图呈现在PPT上，还可以作下面分析线面垂直的判定时，对垂直于面内一条或两条平行直线否定的直观依据。）

（二）关于直线与平面垂直判定定理的教学

在直线与平面垂直的判定定理的探究环节，教科书安排了一个“探究”实验：通过翻折三角形纸片，探究如何翻折才能使折痕AD与桌面所在的平面垂直。如何用好书上这个“探究”实验？在折纸试验中如何让学生经历操作、观察、合情推理（归纳和类比）便成了这个判定定理教学设计的一个关键问题.

教科书安排的试验是这样的，准备一块三角形纸片，过三角形ABC的顶点A翻折纸片，得到折痕AD（如图3），将翻折后的纸片竖起放置在桌面上（BD、DC与桌面接触）

思考：

（1）随意折纸，折痕 AD一定与桌面垂直吗？

（2）折痕与桌面垂直的学生思考这种垂直关系形成的原因；没垂直的学生改进折法，并尝试归纳方法。

显然，“过三角形ABC的顶点A翻折纸片”这样的条件是没有必要的，而且纸片是三角形的原因完全是三角形是边数最少的平面图形，采用三角形纸片可以减少边数对学生的干扰。因而，对这部分内容作如下三方面的创新：

1.引导学生分析，如果借助直线与平面内的直线的垂直关系来判定直线与平面垂直，那么最少猜想是几条？在否定了一条和两条平行直线之后，引出对两条相交直线的探究。在利用直观的折纸试验之前，介绍对判定方法的演绎推理在后续的选修教材中利用空间向量证明，使学生明白直观感知对立体几何问题研究的必要性，也明白归纳推理是需要演绎论证的。

2.拿出课前准备好的三角型纸片，请同学们随意折一下，将纸片立于桌面上（两底边与桌面接触），观察折痕所在直线与桌面的位置关系，并与学生一起比较折痕与桌面垂直和不垂直的作品，提出两个任务：一是没做到垂直的同学将其修改为垂直，二是所有同学思考并交流如何折才能使折痕与桌面垂直？

3.解释纸片形状的任意性，只要有一条直边即可，其它边可以是曲边，即便是半圆形也可以。脱去表象，注重本质——垂直于面内的两条相交直线。

（三）关于渗透数学思想方法的教学

结合空间点线面之间位置关系的研究方法和本课的探究内容，体现“空间问题转化为平面问题”、“立体几何平面化”及“降维”、“无限转化为有限”的数学思想。“转化”是本课的核心思想，重要的是让学生在知识的探究学习中去体验与领悟。在直线与平面垂直的定义、判定定理和例题中都隐含了线线垂直与线面垂直的反复转化关系，为了学生可以很清晰地领悟和应用转化关系解决问题，也为后面的学习打下基础，笔者在教学的过程中一步步完善了位置关系转化图，并画在黑板上呈现给学生，作为学生理解这部分内容的主线。

三、分析讨论 思维提升

为了完成课标要求，及完成预诊中对本节课教学内容分析和学生情况分析出现的问题，整节课围绕“双互动，四统一”的教学范式展开，希望将课堂变成学生探求知识、发现真理的沃土。在实践的过程中，预诊与实践是螺旋上升的，传统与创新是互补互促的，教师要有智慧、懂反思。

立足课标、立足以学生为本设计本节课，一直想挣脱传统的束缚，在创新中展现数学的风采，所以在授课过程中也出现很多不足，比如课堂小结不完善，引导语言不够精炼、指向性不强等。单个教师的行动研究的规模小，易于实施，但力量单薄，很难从事深入的、细致的、说服力强的研究，因而我们需要由专业研究人员、教师、学校行政领导参加的有较强的理论指导，研究力量大的理想的行动研究。通过对本节课的研究，笔者明白一个道理，传统与创新是不相悖的，传统是创新生长的沃土，创新是回报传统的硕果。

[1]杨小微.教育研究的理论与方法[M].北京: 北京师范大学出版社, 2008.

[2]张玉彬.理想课堂的构建与实施[M].重庆: 西南师范大学出版社, 2011.