基于机器视觉的元件角度偏移算法研究

2014-07-20贾宝娟李志强秦芹芹张菲菲

机械工程与自动化 2014年4期

贾宝娟，李志强，秦芹芹，张菲菲

（山东科技大学机械电子工程学院，山东青岛 266590）

0 引言

随着电子产品微型化的发展趋势和贴装密度的增加，各种全自动贴片机对贴装精度和速度的要求越来越高，因此对贴片元件的检测也越来越重视。由于贴片机吸嘴在吸取元件时可能会造成元件的偏移，而元件的角度是进行贴装角度矫正、贴装位置补偿和元件尺寸计算的核心，也是视觉检测的关键。因此，为了能得到精确的位置补偿数据，使贴片元件能够准确地贴装到PCB板上，必须对元件的角度进行偏移检测。

1 图像预处理算法

1.1 图像灰度化

灰度化是图像处理的基础，图像灰度化方法主要有3种：最大值法，平均值法，加权平均值法。由理论分析可知，加权平均值法能得到效果比较好的灰度图像，故本文采用加权平均值法对原始图像（如图1 所示）进行了灰度化处理，处理结果如图2 所示，对应的灰度直方图如图3 所示。

图1 原始图像

图2 灰度化图像

1.2 图像的增强

1.2.1 图像的中值滤波

中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近真实值，从而消除孤立的噪声点。二维中值滤波输出为：

g（x，y）＝med｛f（x－k，y－l），（k，l∈W）｝.

其中：f（x，y），g（x，y）分别为原始图像和处理后图像的灰度值；W为二维模板，通常为2＊2，3＊3，5＊5区域。

中值滤波结果如图4 所示。

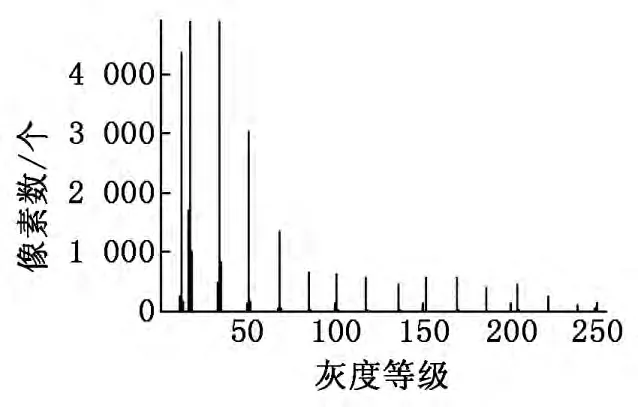
图3 灰度化图像的灰度直方图

1.2.2 图像的线性灰度变换

灰度变换是图像增强的一种重要手段，它可以使图像更加清晰，特征更加明显。为了突出图像中感兴趣的目标，相对抑制那些不感兴趣的地方，可以采用分段线性法。为了增强对比度，一般采用三段线性变换法，其数学公式为：

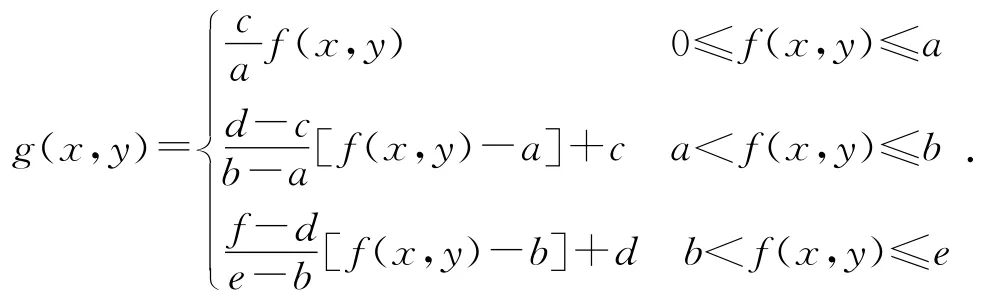
其中：a，b，e为原始图像划定的灰度值；c，d，f为对应的扩展或压缩后图像的灰度值。

图4 中对灰度区间［a，b］进行了线性扩展，而灰度区间［0，a］和［b，e］受到了压缩。线性变换结果如图5 所示，对应的灰度直方图如图6 所示。

图4 中值滤波结果

图5 线性变换的图像

图6 线性变换图像的灰度直方图

1.3 图像的二值化

图像的二值化就是将图像上像素点的灰度值设置为0或255，也就是将整个图像呈现出明显的只有黑和白的视觉效果。比较常用的方法有双峰法、迭代法和最大类间方差法（OTSU）等，本文着重介绍最大类间方差法。设一幅图像的灰度值为0～m－1级，m为256；灰度值为i的像素数为ni，然后用k将其分成两组：C0＝｛0～k－1｝和C1＝｛k～m－1｝，各组产生的概率分别为：

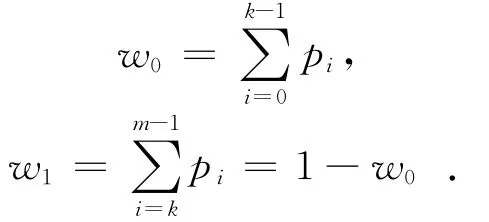
其中：pi为各灰度值的概率。C0，C1类像素的平均值分别为：

最大类间方差为：

其中：u为整体图像灰度平均值。

令k从1～m－1变化，计算出不同k值下的σ2（k）值，令σ2（k）产生最大值的那个k就是所需要的阈值。本文主要通过Matlab将算法自主编程来实现最大类间方差法，图像二值化结果如图7 所示。

1.4 边缘检测算法

在图像处理技术中，许多场合都要求用计算机进行图像描述并对图像进行分析和理解，而边缘检测是图像分析和处理的关键。边缘检测的方法很多，如梯度算子、Roberts算子、拉普拉斯算子以及Canny法等。Canny边缘检测是一种比较新的边缘检测算子，具有很好的边缘检测性能，本文采用Canny边缘检测，处理结果如图8 所示。