叶序排布磨粒对砂轮的磨削温度场效应❋
2014-07-20张洪雷吕玉山
张洪雷,吕玉山,王 军
(沈阳理工大学 机械工程学院,辽宁 沈阳 110159)
0 引言
研究磨削温度与磨削区温度的分布具有很重要的意义[1]。而对于磨粒的有序化排布,国内外学者也进行了深入的研究。Aurich J C等提出有序化排布超硬磨料电镀砂轮,基于几何模型,通过运动学仿真不同的磨料排布方式,应用仿真结果设计制造出最佳有序排布电镀砂轮的结构,并通过实验证明其一些磨削性能得到提高[2,3]。Koshy P等通过控制磨料之间轴向距离和相邻行的轴间距来减低工件表面粗糙度,实验表明磨料的偏移排布使工件的表面粗糙度得到适当的改善[4]。但是,这些学者的研究都没有涉及到磨粒有序化砂轮的温度场问题,本文将生物学中的叶序排布理论应用于CBN砂轮的磨粒排布设计中,采用ANSYS中的热分析法,研究磨粒叶序排布的电镀CBN砂轮的叶序系数和磨削工况条件变化时的磨削区温度场的变化规律。
1 叶序理论简介
植物叶序最常见的排列方式为互生叶序,在茎的每一节只生有一叶。对互生植物来说,就是任相邻两颗果实间的相对位置是相同的,这样决定了互生植物叶子分布规律的因素就只有两个[5]:①相邻两颗果实中心在茎方向上的距离;②相邻两颗果实中心对茎的夹角。正常情况下植物叶序分数对应着以下序列:

上述序列中分子代表叶序线绕茎的圈数,比值代表了一片叶子所占的圈数。易知上述序列是斐波那契序列:1,1,2,3,5,8,…,Fn,…的隔项之比,这个比的极限为:

可以验证当生长角为0.328时,才可以保证新增的一片叶子不会在之前的任一片叶子的正上方。
本文所用的CBN砂轮所用的磨粒就是基于这种规律排布的。该CBN砂轮磨粒排布规律满足叶序理论中的柱面坐标下的叶序点排布模型,其表示为[6]:

其中:n为磨粒的序号;φ(n)为序号为n的磨粒的角度;H(n)为序号为n的磨粒的高度;h为叶序系数;α为常数,取黄金分割角137.508°。
叶序排布可以实现空间最大包裹,保证磨粒的排布均匀性和互补性。磨粒按照叶序分布规律设计的砂轮模型如图1 所示。
2 磨削温度场热源模型的建立
由于磨削过程的复杂性,故做如下假设:
(1)磨削过程是许多磨粒随机切削的过程,许多随机磨粒点热源的集合可近似认作是一个连续分布的平面热源;假设它是一个持续发热的均匀而恒定的面热源,即均布热源,其单位时间单位面积的发热量为qm。
(2)假设磨削时产生的热量传入工件的百分比为Rw:

其中:λw为工件的热导率;λs为CBN磨粒的热导率。热源发热强度qm为:

其中:q为磨削区总的发热强度;s为砂轮与工件接触面积;Ft为磨削切向力;vs为砂轮速度;ls为接触弧长;b为工件宽度。
(3)由于磨粒是按叶序规律排布的,磨粒的平均间距可以计算。当叶序系数变化时,导致磨粒数量、磨粒平均间距的变化,进而影响接触弧长。在一个切平面内,两个相邻磨粒磨过的轨迹如图2 所示。
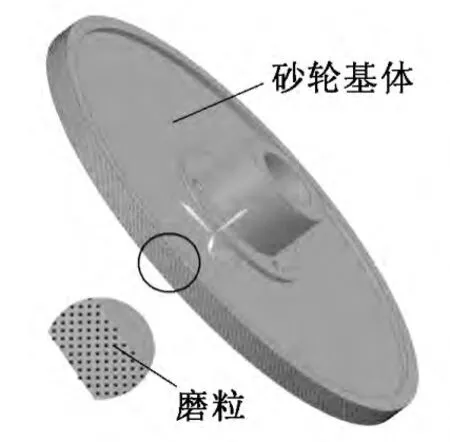
图1 叶序排布砂轮磨粒形貌图

图2 砂轮接触弧长示意图
图2 中,l1为第一颗磨粒的轨迹长度,l2为第二颗磨粒的切削长度,以后的磨粒的切削长度也是l2,磨粒所走的轨迹都是摆线,可以确定l1方程为:

其中:rs为砂轮半径;ω为砂轮角速度;vw为工件进给速度;t1为相邻两个磨粒转到切削位置所间隔的时间;t为磨削时间。

其中:ld为磨粒平均间距;r为磨粒半径。
将式(7)、式(8)代入式(6)中,得:

对式(10)进行弧长积分,通过用 MATLAB数值积分可以计算l2的长度,即热源长度ls。当叶序系数h变化时,l2的变化规律如图3 所示。
根据上述情况,平面磨削时工件传热学模型可近似看作一个无限宽有限长的运动面热源对半无限大导热体的二维导热作用问题,从而分析不同叶序系数下磨削温度场的分布情况并解释它们之间的差别。
3 平面磨削温度场的仿真过程
3.1 边界条件的设定与有限元模型建立
由以上对磨削温度场的各种假设,可把工件假设成矩形,磨削工艺条件如表1所示。被磨45钢工件的导热性能如表2所示。假定工件的初始温度和外界环境一致(θ0=20℃),工件各面与空气绝热。建立的有限元模型如图4 所示。

图3 叶序系数与接触弧长的关系

表1 磨削工艺参数

表2 工件的比热容C和热导率λ与温度的关系
3.2 热流密度计算
叶序系数为0.001时的磨削切向力可以根据经验公式计算。根据磨削切向力与接触弧长和磨粒平均间距的比例关系,可以得出叶序系数与磨削切向力的关系,如表3所示。已知磨削切向力,可以由式(4)求得需要施加的热流密度。

图4 工件的有限元模型

表3 叶序系数与磨削切向力的关系
3.3 计算过程
在建立了有限元模型后,需要对模型进行热源加载,施加上述初始条件和边界条件,并在磨削工件表面添加一个如图5 所示的移动热源。由于ANSYS本身不能直接加载移动热源,所以把此过程离散化,在极短的时间内在某一磨削区加载一固定热流密度,在下一时间段内移至另一区域加载固定热源,将之前的加载清零,并把上一次所得的计算结果作为这一次的初始条件。经过30次循环迭代和逐步加载,就可得到磨削区温度分布。
4 仿真结果及分析
图6 为计算获得的工件磨削温度场分布形态,图7 为被磨工件表面的温度分布。

图5 三角形热源加载过程

图6 不同叶序系数下的工件磨削温度场形态

图7 工件表层温度分布
由图6 可以直观地看出:不同叶序系数下都是磨削区温度最高,且从表层向内温度梯度变化较大;不同叶序系数下,温度梯度分布基本相同,随着叶序系数增大,各个梯度的温度都有所下降。
由图7 可以看出:随着计算节点距离的增大,在距离工件磨削起点为29mm处温度达到磨削接触区域的最高温度的稳定状态;在距离为29.5mm处是磨削接触区域的温度最高处;在距离大于29.5mm后,温度开始下降,趋于常温,该区域为磨削工件的待磨削区域。由图7 还可以看出:随着叶序系数的增大,最高磨削温度也随之减小。
对于图6 、图7 所显示的现象的产生原因是,根据式(2),在磨料排布时,随着叶序系数h的增大,单层磨料砂轮表面磨粒数减小,继而导致磨削力的下降(见表3),同时磨粒的平均间距也加大,有足够排屑冷却空间,则磨削温度和温度场的梯度也随之降低。
5 结论
叶序排布单层磨料砂轮磨削区的温度场分布呈现出不均匀性,磨削接触区的表层温度最高。叶序系数的变化对磨削接触区域的温度场有较大的影响。在本仿真计算的磨削条件下,随着叶序系数的增大,磨削表面温度趋于下降,表层相对底层的温度梯度也降低。
[1]任敬心,华定安.磨削原理[M].西安:西北工业大学出版社,1988.
[2]Aurich J C,Braun O,Wamecke G.Development of a superabrasive grinding wheel with defined grain structure using kinematic simulation [J].Annals of the CIRP,2003,52(1):275-280.
[3]Aurich J C, Herzenstiel P,Sudermann H,et al.High-performance dry grinding using agrinding wheel with a defined grain pattern[J].Annals of the CIRP,2008,57(1):357-362.
[4]Koshy P,Iwasaki A,Elbestawi M.Surface generation with engineered diamond wheels:insights from simulation[J].Annals of the CIRP,2003,52(1):271-274.
[5]柴中林,王兰州.叶序角的最优性分析[J].生物数学学报,2005,20(1):71-76.
[6]Prusinkiewicz P,Lindenmayer A,Hanan J S,et al.The algorithmic beauty of plants[M].New York:Springer-Verlag,1990.
